Unsupervised Learning: Hauptkomponentenanalyse (PCA)

DS3 - Vom experimentellen Design zur
explorativen Datenanalyse & Data Mining

Saskia Otto & Monika Eberhard

Universität Hamburg, IMF

Wintersemester 2025/2026

Lernziele

Am Ende dieser VL- und Übungseinheit werden Sie

die Grundlagen der Hauptkomponentenanalyse (im Englischen ‘Principal Component Analysis’ oder PCA) verstanden haben, einschließlich des Ziels, die Dimensionalität von Daten zu reduzieren und die wichtigsten Informationen zu extrahieren.
in der Lage sein, die Unterschiede und Gemeinsamkeiten zwischen Clusteranalyse und PCA zu verstehen und zu erklären.

Principal Component Analysis (PCA)

Ordinationstechniken

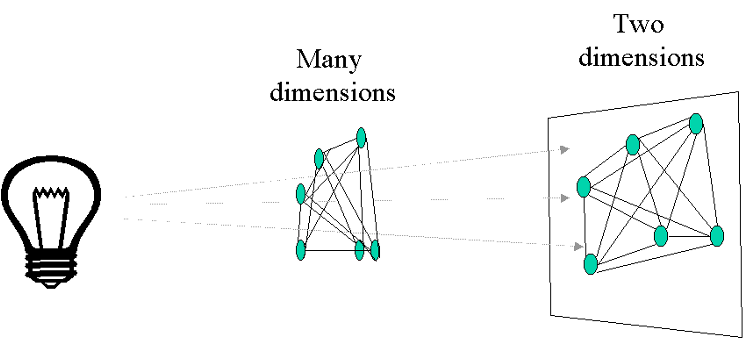
Durch mathematische Verfahren wird eine sog. Dimensionsreduktion durchgeführt, so dass die Lage der Daten in einem zwei- oder dreidimensionalen Koordinatensystem dargestellt werden kann.
Dabei werden Objekte (z. B. Standorte) oder Variablen (z. B. Arten) geometrisch so angeordnet, dass die Abstände zwischen ihnen im Diagramm ihre natürlichen Abstände darstellen.
- Nahe beieinander liegende Standorte im Diagramm werden als ähnlich in z.B. der Artenzusammensetzung interpretiert.
Die Achsen des Diagramms stellen neue Variablen dar, die Zusammenfassungen der ursprünglichen Variablen sind.
Die meisten Methoden beruhen auf der Extraktion der Eigenvektoren einer Assoziationsmatrix.

Beispiele für Ordinationsverfahren

PCA (Principal Component Analysis, Hauptkomponentenanalyse)
CA (Correspondence Analysis, Korrespondenzanalyse)
MDS (Multidimensional Scaling, Multidimensionale Skalierung)
CCA (Canonical Correspondence Analysis, Kanonische Korrespondenzanalyse)
DCA (Detrended Correspondence Analysis)
RDA (Redundanz-Diskriminanz-Analyse)

PCA - Hauptkomponentenanalyse

stellt die wichtigste eigenvektorbasierte Methode, arbeitet mit quantitativen Daten und bewahrt den euklidischen Abstand zwischen den Objekten.
findet eine Folge von Linearkombinationen der Variablen, die eine maximale Varianz aufweisen und untereinander unkorreliert sind.
dient nicht nur als Werkzeug zur Datenvisualisierung, sondern erzeugt auch abgeleitete Variablen zur Verwendung in überwachten Lernproblemen.
Abstände zwischen Objekten im sog. Biplot sind eine Annäherung an ihre euklidischen Abstände im multivariaten Raum → Standardisierung bei Abundanzdaten und Daten mit unterschiedlichen Einheiten!
Voraussetzungen:
- lineare Beziehung zwischen den Variablen
- Datensätze sollten multivariat normalverteilt sein
- keine fehlenden Werte

PCA - “Geometrischer” Ansatz | 1

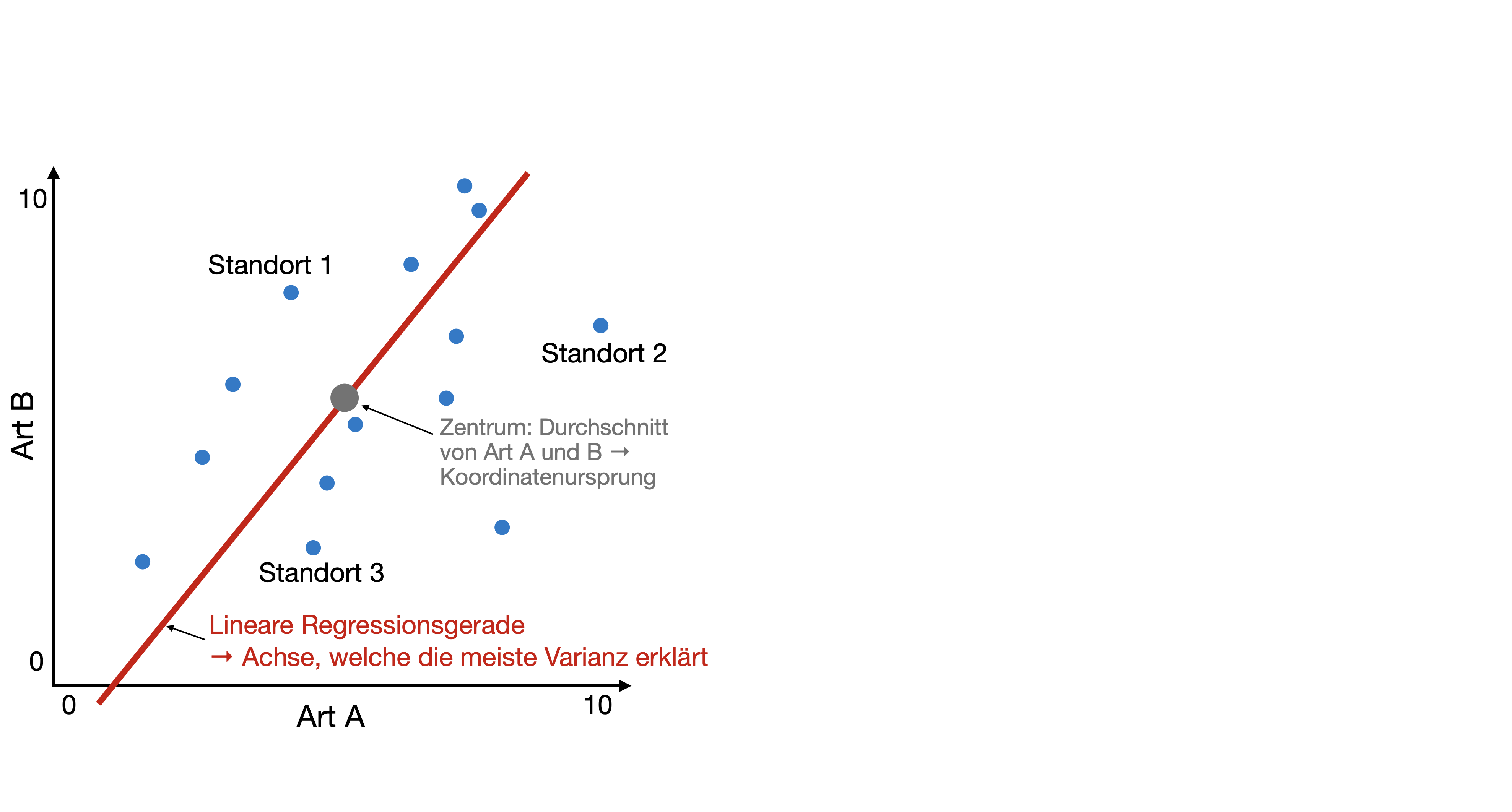
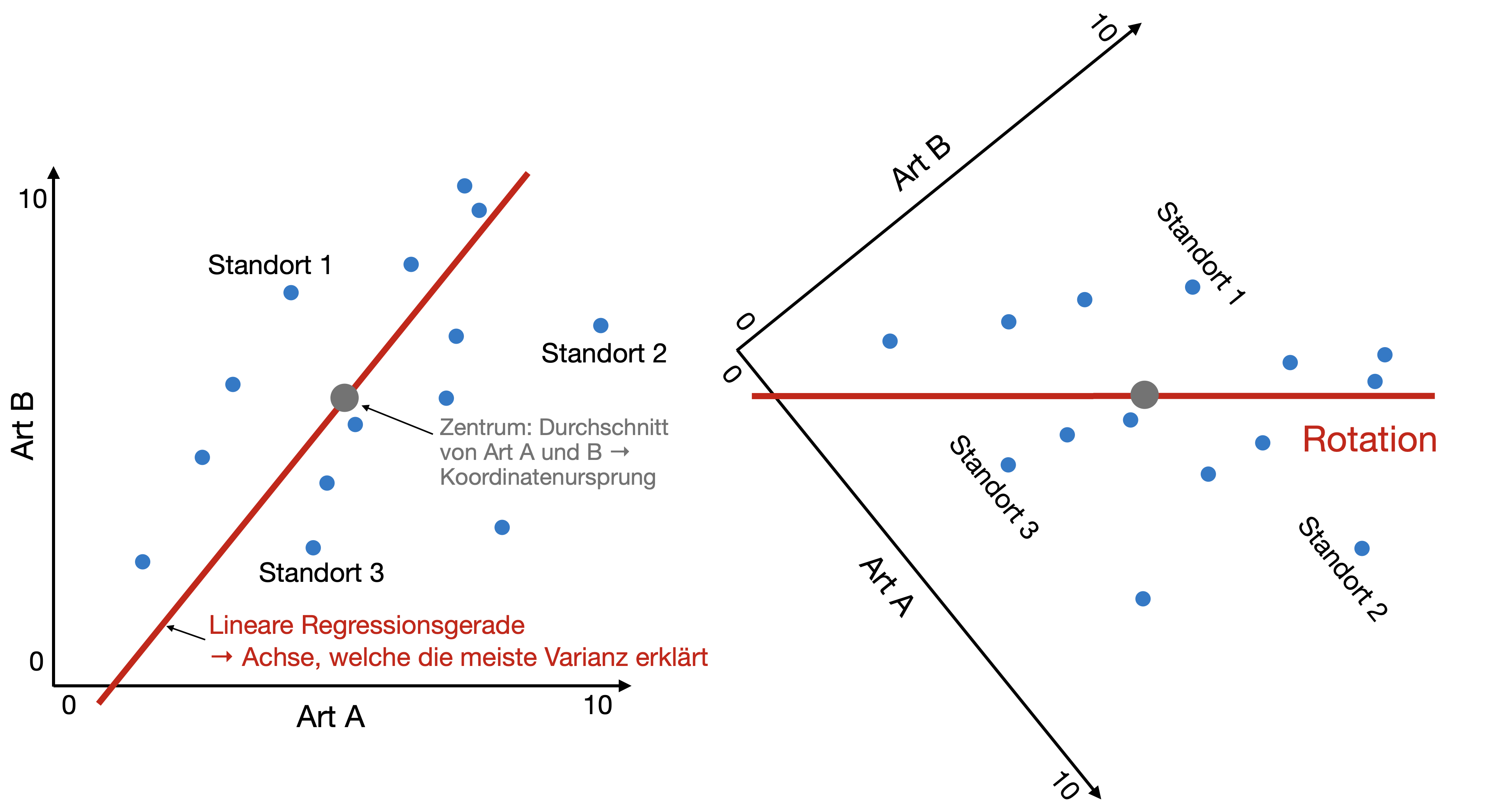
Ursprung des neuen Koordinatensystems wird in die Mitte der Datenpunkte verschoben (Zentrierung).
Rotation des neuen Koordinatensystems, bis die Varianz der 1. Achse maximiert ist (Reduzierung der Restvarianz).

PCA - “Geometrischer” Ansatz | 2

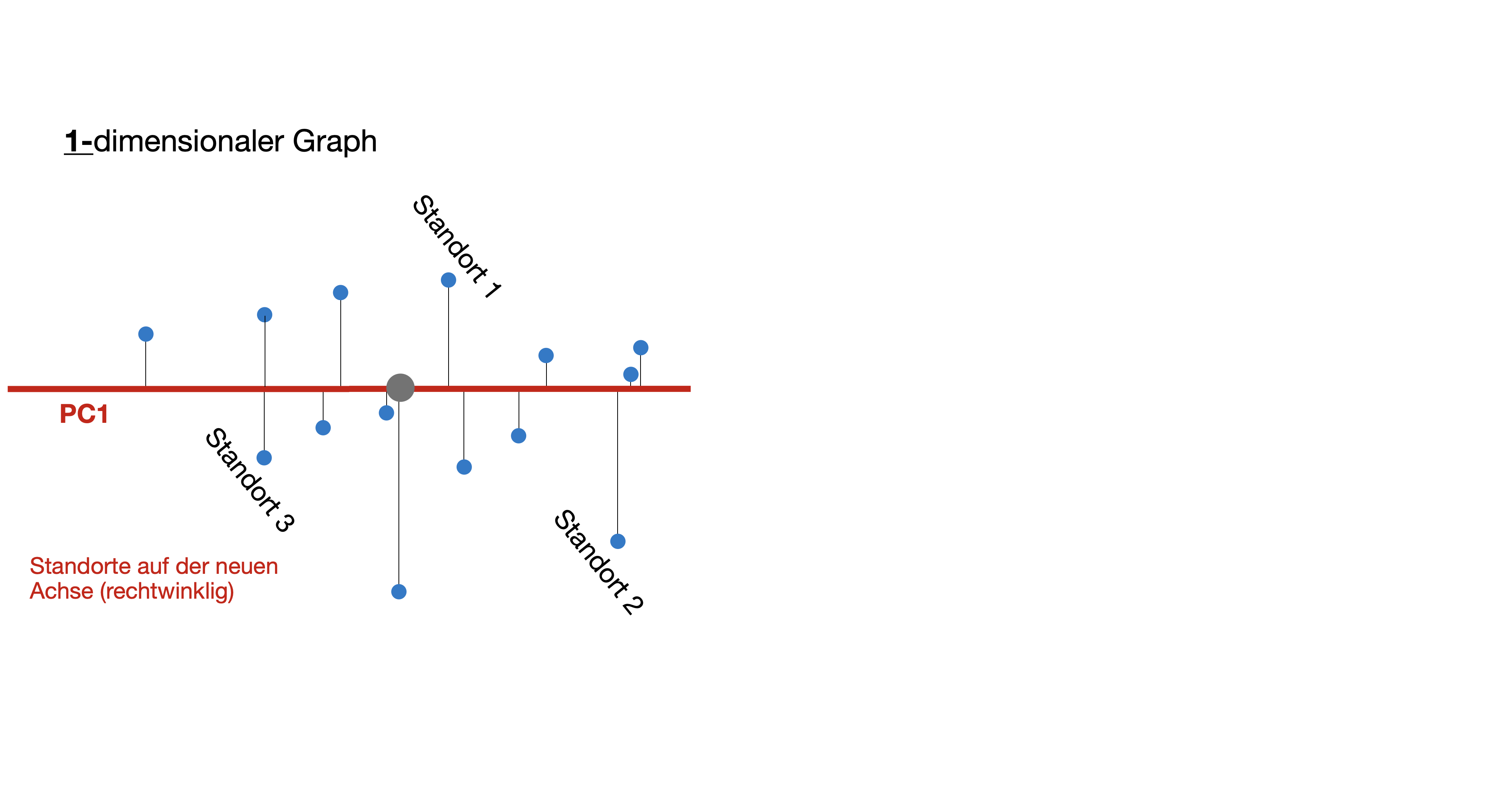
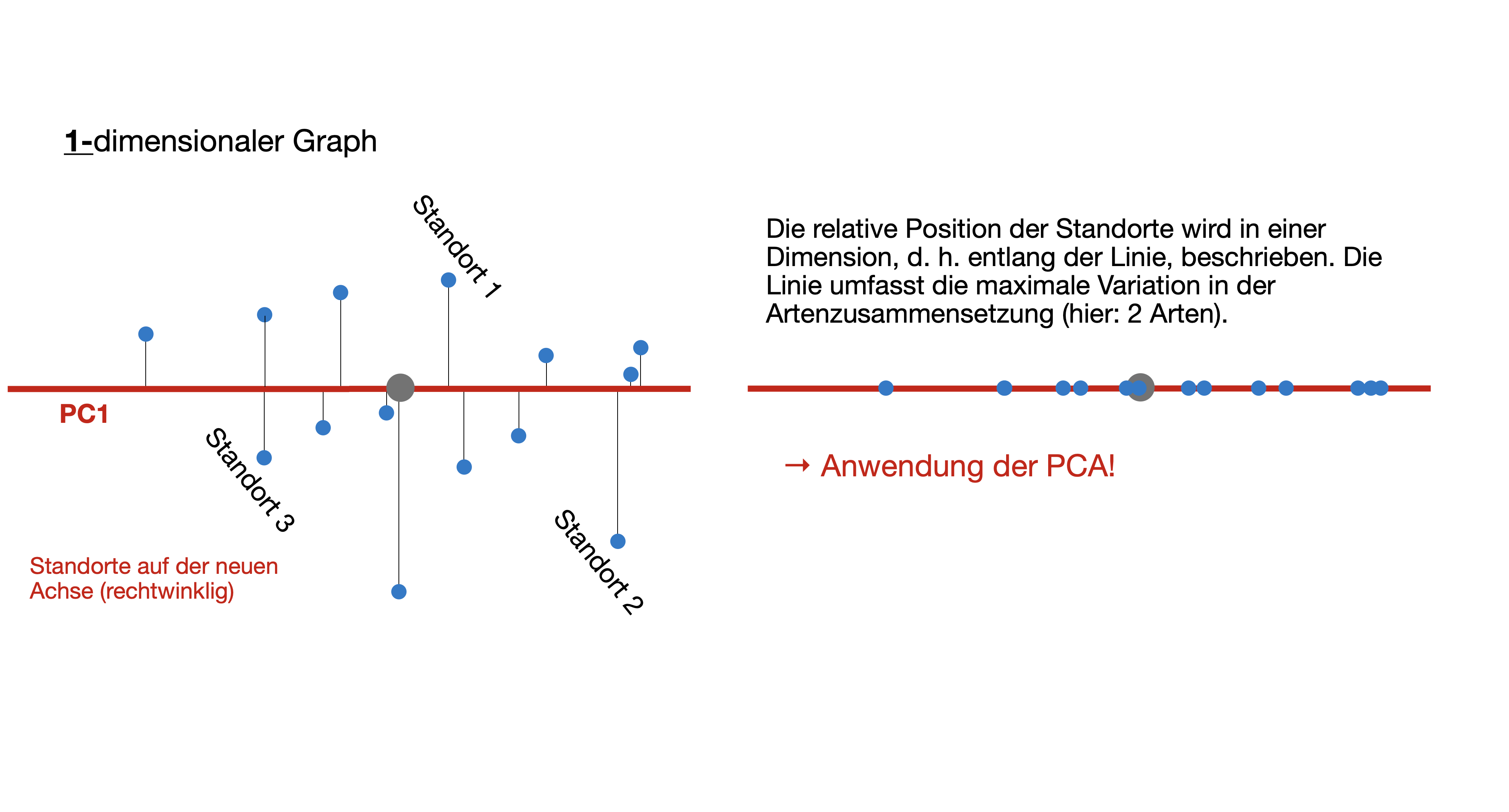
Ursprung des neuen Koordinatensystems wird in die Mitte der Datenpunkte verschoben (Zentrierung).
Rotation des neuen Koordinatensystems, bis die Varianz der 1. Achse maximiert ist (Reduzierung der Restvarianz).

PCA - “Geometrischer” Ansatz | 3

Zusätzliche Achsen müssen unabhängig voneinander sein (=orthogonal).
Visualisierung der reduzierten Dimensionen als sogenanntes “Biplot” (d.h. nur ein Teil der Variation im ursprünglichen Datensatz wird dargestellt).

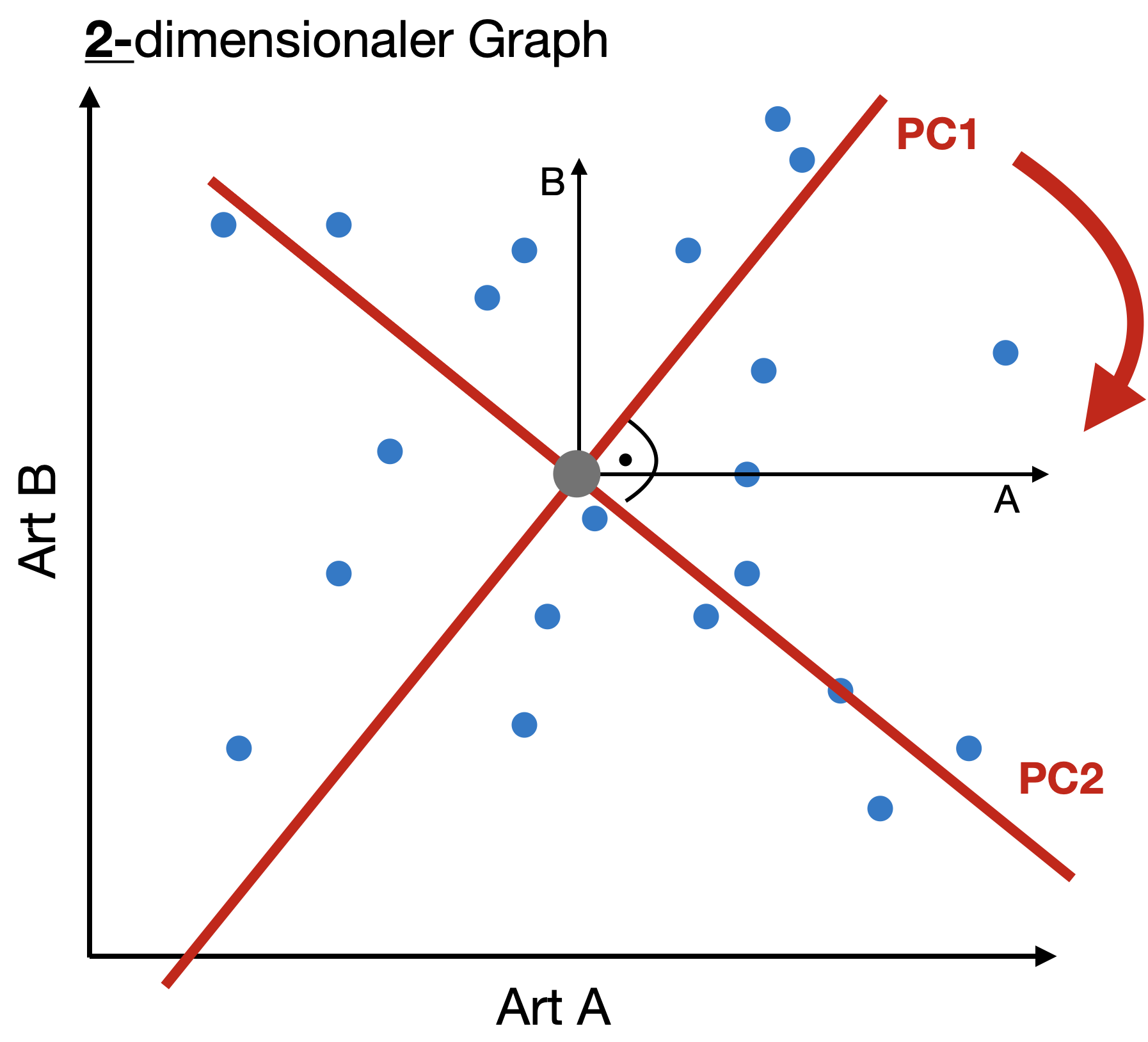
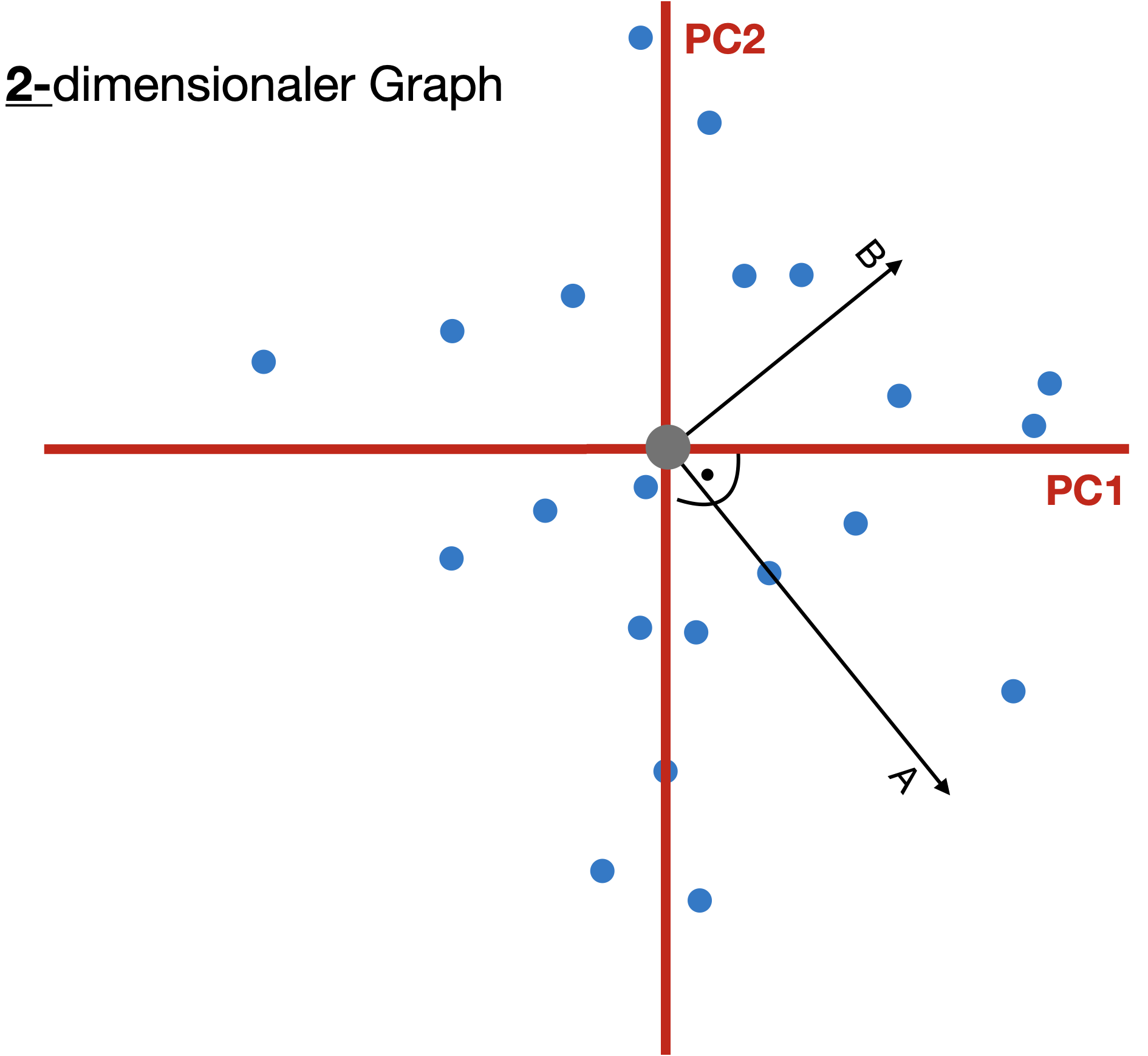
Scores: Koordinaten von Objekten (hier Standorte) entlang des hypothetischen Gradienten PC1 zu PC2.

Loadings: Koordinaten des Vektorscheitels entlang des hypothetischen Gradienten → Maß für die Korrelation mit den PC-Achsen.

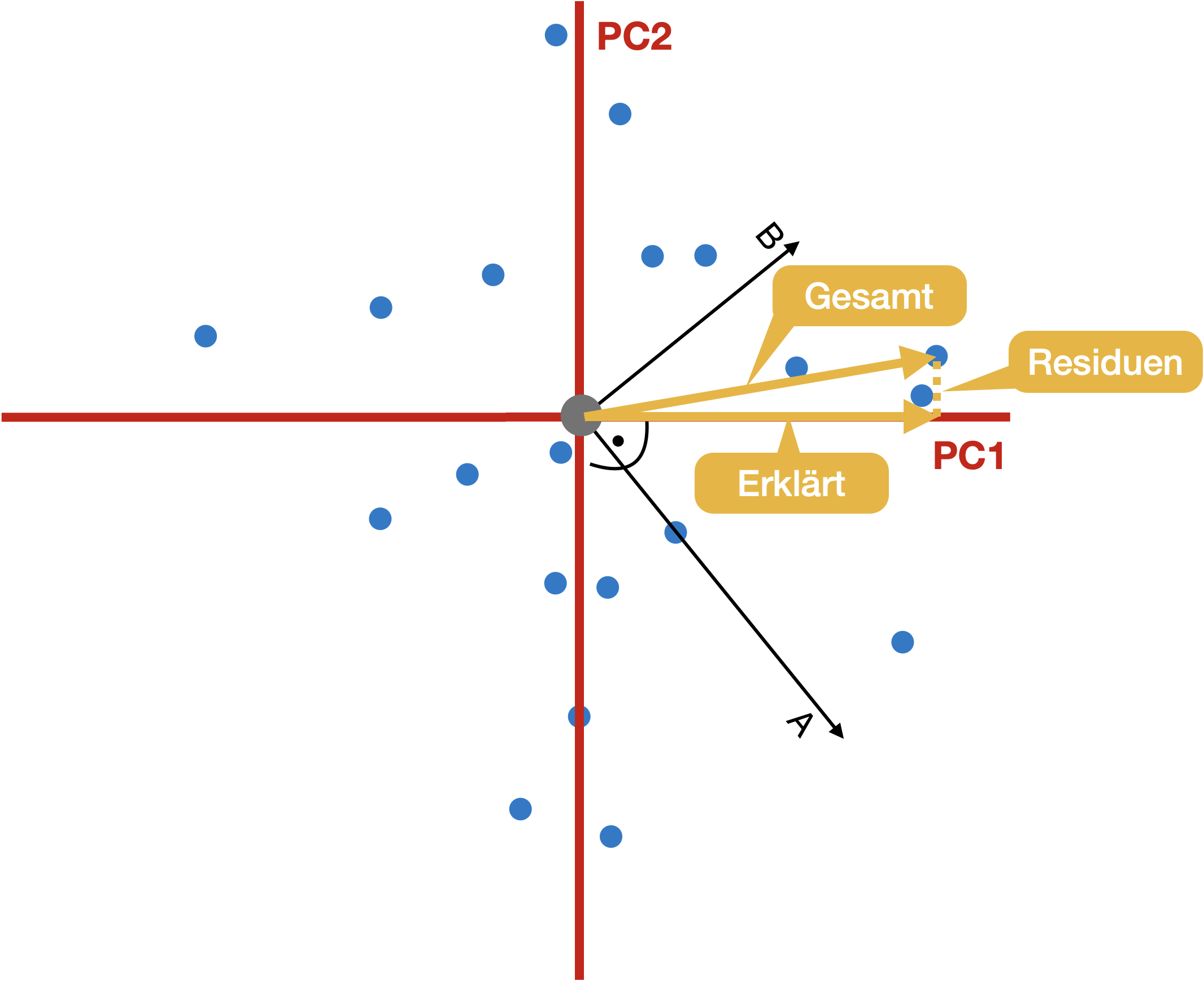
PCA - “Geometrischer” Ansatz | 4

Gesamtvariation: Summe der quadrierten Abstände vom Ursprung
Erklärte Varianz: Summe der quadrierten Projektionen auf die Hauptkomponenten (PC) = λ (Eigenwerte)
Residuale Varianz: Summe der quadrierten orthogonalen Abstände zu den Hauptkomponenten
Nur eine Rotation: Alle Achsen/Hauptkomponenten erklären die Gesamtvarianz!

PCA - Mathematischer Ansatz

Die erste Hauptkomponente Z₁ eines Satzes von Variablen X₁, X₂, X₃, ..,X_p ist die normalisierte lineare Kombination dieser Variablen, welche die größte Varianz hat:

Z_1 = \phi_{11}X_1 + \phi_{21}X_2 + ...+\phi_{p1}X_p

Die Koeffizienten \phi_{11}, .., \phi_{p1} repräsentieren die Ladungen (‘loadings’) der ersten Hauptkomponente; zusammen bilden diese den Hauptkomponenten-Ladevektor, \phi_1 = (\phi_{11}, \phi_{21},.., \phi_{p1})^T.
Die Ladungen werden so eingeschränkt, dass ihre Quadratsumme gleich eins ist, da andernfalls die Festlegung dieser Elemente auf einen beliebig großen Absolutwert zu einer beliebig großen Varianz führen könnte (Normalisierung).

Berechnung der PC ‘Scores’

Angenommen wir haben einen n x p Datensatz (n Zeilen und p Spalten), dann lässt sich jeder Datenpunkt im ursprünglichen Raum durch die lineare Kombination der Hauptkomponenten repräsentiert = PC ‘Score’ z_{ik}:

z_{ik} = \phi_{1k}x_{i1} + \phi_{2k}x_{i2} + ...+\phi_{kk}x_{ip}

mit i=1 bis n als Stichprobenumfang (= Anzahl Objekte) und k=1 bis p Hauptkomponenten

In Matrixform ausgedrückt: \mathbf{Z} = \mathbf{X}*\mathbf{U}

Matrix Z:

Datenpunkte entlang der neuen Hauptkomponenten (PC-Achsen) z_{ik} \rightarrow \mathbf{Z} =\left( \begin{array}{ccc} z_{11} & \cdots & z_{1k} \\ \vdots & \ddots & \vdots \\ z_{i1} & \cdots & z_{ik} \end{array} \right)

(Zentrierte) Datenmatrix X:

Variablen X_k in i Beobachtungen x_{ik} \rightarrow \mathbf{X} =\left( \begin{array}{ccc} x_{11} & \cdots & x_{1k} \\ \vdots & \ddots & \vdots \\ x_{i1} & \cdots & x_{ik} \end{array} \right)

Matrix U der k Eigenvektoren:

Regressionskoeffizienten/Ladungen \phi_{kk} \phi_{kk} \rightarrow \mathbf{U} =\left( \begin{array}{ccc} \phi_{11} & \cdots & \phi_{1k} \\ \vdots & \ddots & \vdots \\ \phi_{k1} & \cdots & \phi_{kk} \end{array} \right)

Durchführung in R

Manuelle Berechnung (in R)

Für ganz interessierte…

myPCA <- function(X) {
  X_mat <- as.matrix(X)
  object_names <- rownames(X)
  var_names <- colnames(X)
  
  ### 1. Zentrierung der Daten (wird für die Berechnung von Z gebraucht) 
  X_cent <- scale(X_mat, center = TRUE, scale = FALSE)
  
  ### 2. Berechnung der Kovarianzmatrix S
  X_cov <- cov(X_cent)
  
  ### 3. Berechnung der Eigenwerte lambda und der Eigenvektoren v 
  # der Kovarianzmatrix S (s. Legendre & Legendre, 1998, eq. 9.1 und 9.2)
  # Die Eigenwerte und -vektoren erfüllen die Gleichung S*v = lambda*v.
  X_eig <- eigen(X_cov)
  
  # (Eigenwerte sind ein Maß für die Bedeutung (Varianz) der Achsen. Sie 
  # können als "Proportions Explained" (Anteil der erklärten Variation) 
  # ausgedrückt werden, indem sie durch die Summe aller Eigenwerte geteilt 
  # werden.)
  
  ### 4. Eigenvektoren als Matrix U abspeichern
  U <- X_eig$vectors
  rownames(U) <- var_names
  
  ### 5. Matrix Z berechnen
  Z <- X_cent%*%U       # (s. Legendre & Legendre, 1998, eq. 9.4)
  rownames(Z) <- object_names
  
  # Output als Liste mit allen 3 Matrizen
  result <- list(X_eig$values,U,Z)
  names(result) <- c("eigenvalues","U", "Z")
  return(result)
}

myPCA(X = spiderA_hell)

PCA in R

Beispiel mit der PCA() Funktion aus 'FactoMineR'

library(FactoMineR)
pcaA <- PCA(spiderA_hell, scale.unit = FALSE, graph = FALSE)
  # unsere Daten sind bereits standardisiert, daher 'scale.unit = FALSE'
pcaA

**Results for the Principal Component Analysis (PCA)**
The analysis was performed on 28 individuals, described by 12 variables
*The results are available in the following objects:

   name               description                          
1  "$eig"             "eigenvalues"                        
2  "$var"             "results for the variables"          
3  "$var$coord"       "coord. for the variables"           
4  "$var$cor"         "correlations variables - dimensions"
5  "$var$cos2"        "cos2 for the variables"             
6  "$var$contrib"     "contributions of the variables"     
7  "$ind"             "results for the individuals"        
8  "$ind$coord"       "coord. for the individuals"         
9  "$ind$cos2"        "cos2 for the individuals"           
10 "$ind$contrib"     "contributions of the individuals"   
11 "$call"            "summary statistics"                 
12 "$call$centre"     "mean of the variables"              
13 "$call$ecart.type" "standard error of the variables"    
14 "$call$row.w"      "weights for the individuals"        
15 "$call$col.w"      "weights for the variables"

Output extrahieren

# Eigenwerte
pcaA$eig

# Ergebnisse der Variablen
pcaA$var$coord          # Koordinaten
pcaA$var$contrib        # Beiträge zu den PCs in %
pcaA$var$cor            # Korrelation der Variablen mit den PCs
pcaA$var$cos2           # Qualität der Repräsentation

# Ergebnisse der Objekte (hier Standorte)
pcaA$ind$coord          # Koordinaten
pcaA$ind$contrib        # Beiträge zu den PCs in %
pcaA$ind$cos2           # Qualität der Repräsentation

Anteil der erklärten Varianz

Um die Stärke der einzelnen Hauptkomponenten (PCs) zu verstehen, interessiert uns der Anteil der Varianz, der durch die einzelnen PCs erklärt wird (die Summe ist immer 1 bzw. 100%):

pcaA$eig

          eigenvalue percentage of variance cumulative percentage of variance
comp 1  0.2391942862             50.2281942                          50.22819
comp 2  0.1149343105             24.1349530                          74.36315
comp 3  0.0619177247             13.0020476                          87.36519
comp 4  0.0153305527              3.2192490                          90.58444
comp 5  0.0139610114              2.9316603                          93.51610
comp 6  0.0086239473              1.8109350                          95.32704
comp 7  0.0075595385              1.5874207                          96.91446
comp 8  0.0047529702              0.9980720                          97.91253
comp 9  0.0038069611              0.7994204                          98.71195
comp 10 0.0031663955              0.6649086                          99.37686
comp 11 0.0019933060              0.4185725                          99.79543
comp 12 0.0009741778              0.2045667                         100.00000

Es gibt so viele Hauptkomponenten, wie es Variablen gibt: in unserem Fall 12.

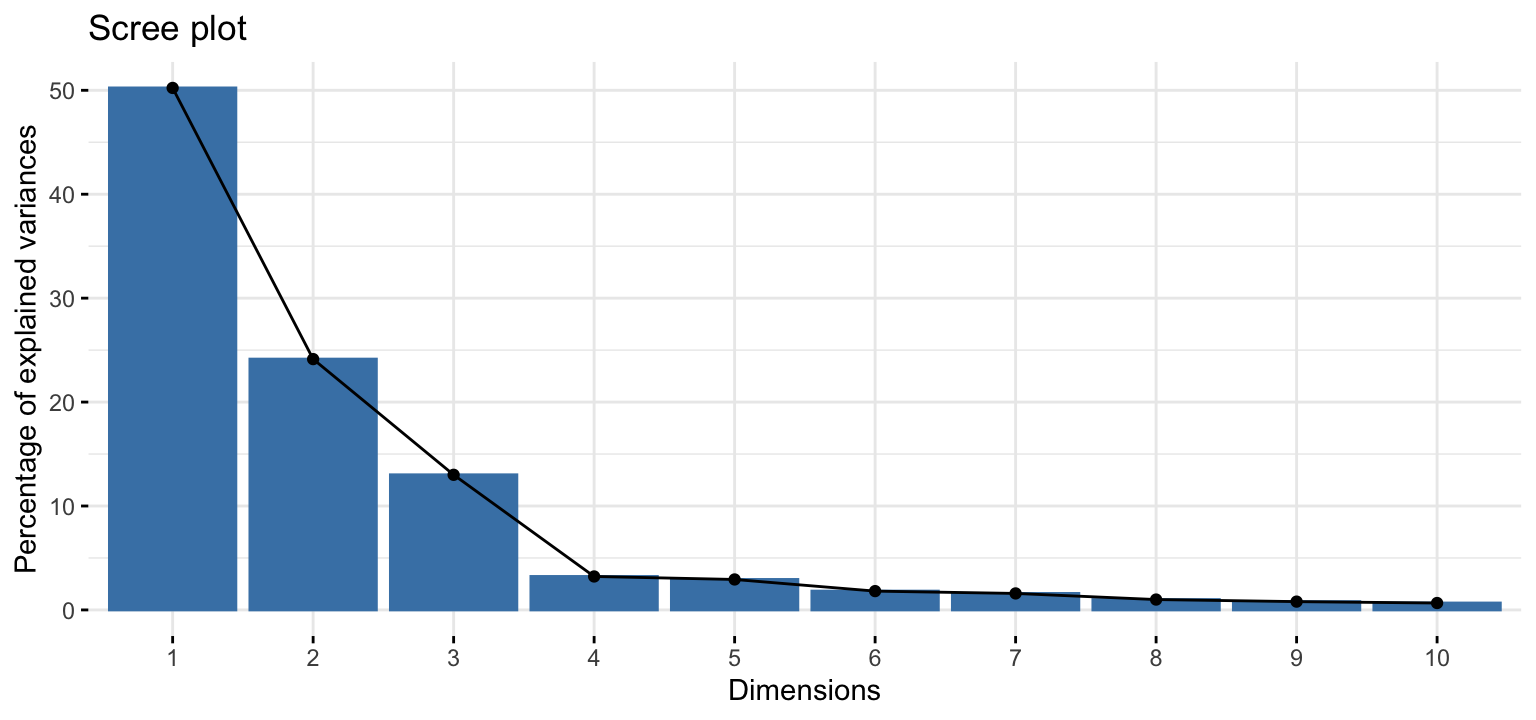
Wie viele Komponenten (PCs)?

Welche Achsen sind wichtig, d.h. wie viel Varianz erklären sie jeweils?
Gibt keine einfache Antwort und keinen Test.
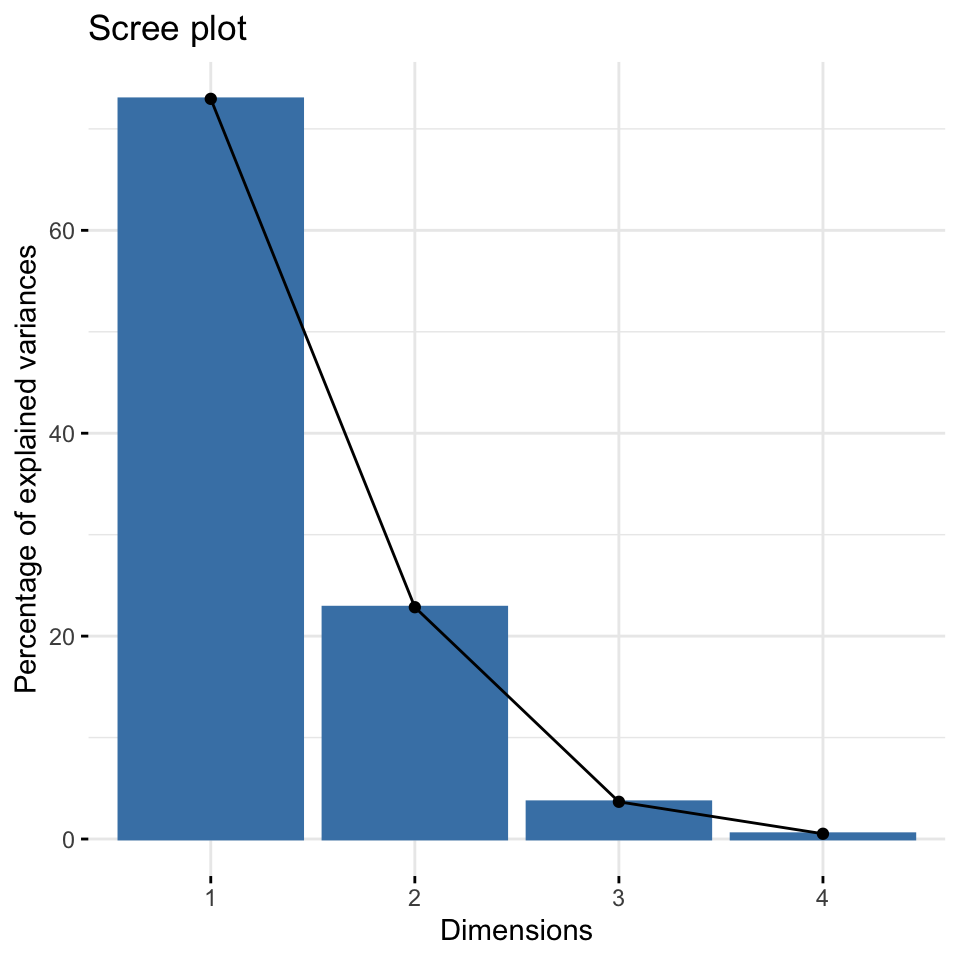
‘Scree plot’ kann als Anhaltspunkt dienen: Wir suchen nach einem “Ellbogen”.

fviz_eig(pcaA)

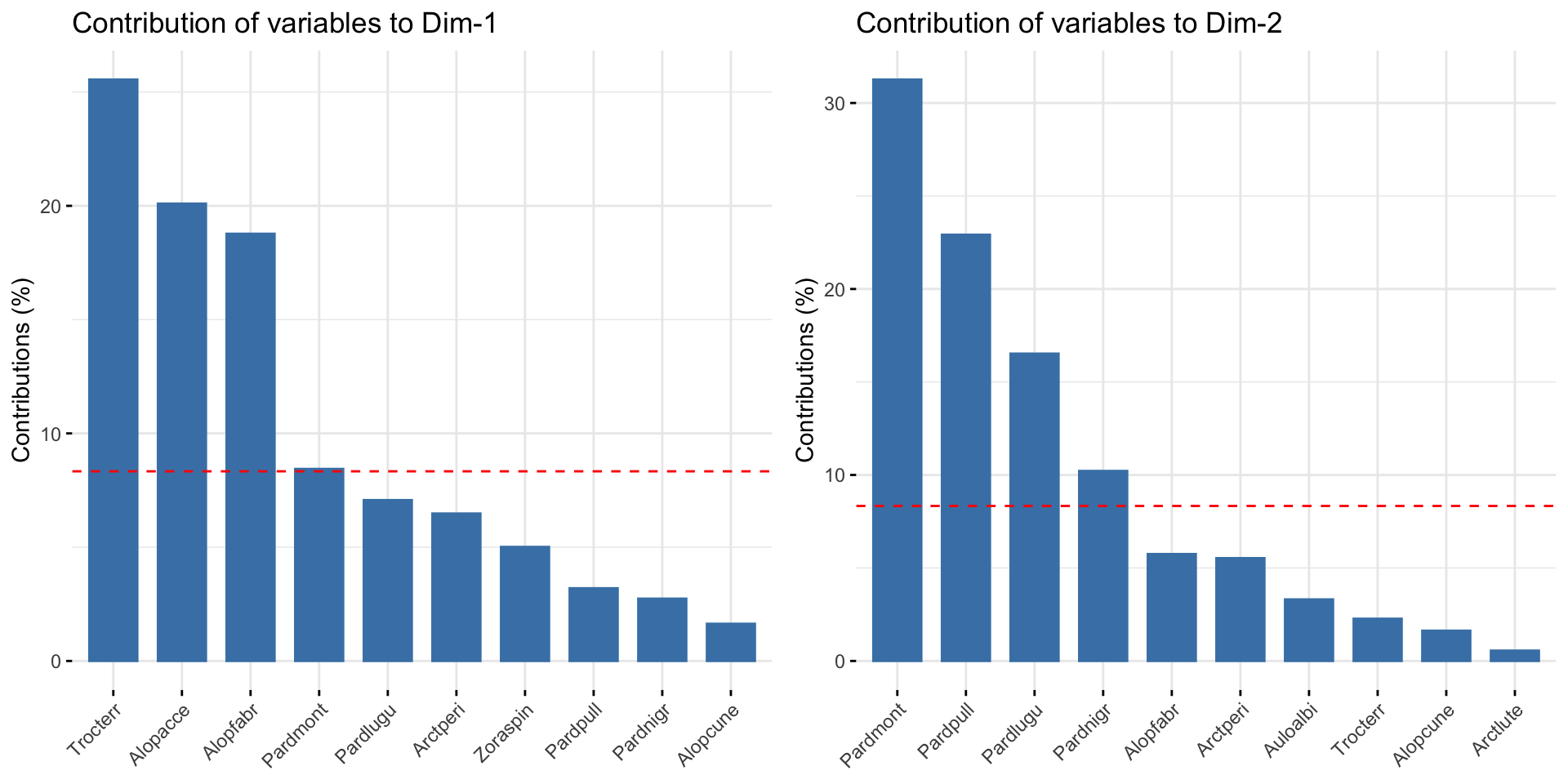
Beiträge der Variablen zu den PCs

p1 <- fviz_contrib(pcaA, choice = "var", axes = 1, top = 10)
p2 <- fviz_contrib(pcaA, choice = "var", axes = 2, top = 10)
gridExtra::grid.arrange(p1, p2, ncol = 2)

Ergebnisse visualisieren | Variablen

Darstellung der Ladungen (‘loadings’) der Variablen entlang der PC1/PC2 Achsen (= Maß für die Korrelation mit den PC-Achsen) mit fviz_pca_var():

Code

fviz_pca_var(
  X = pcaA,  # das PCA Objekt
  repel = TRUE, # Labels sollen nicht ueberlappen
  col.var = "contrib", # Variablenpfeile entsprechend dem Beitrag zur PC1/PC2 einfaerben
  gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07") # Farbwahl
)

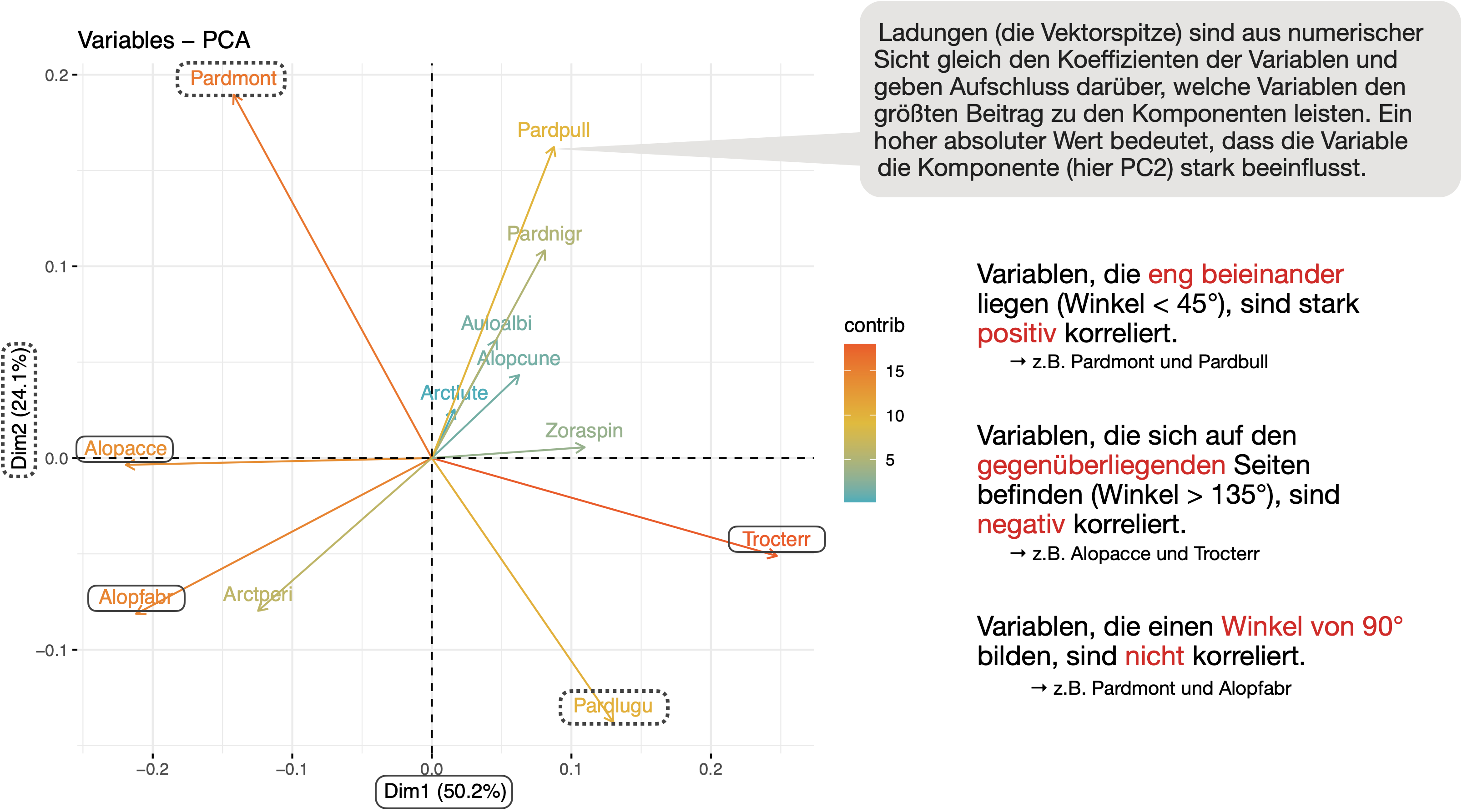
Ergebnisse visualisieren | Objekte

Darstellung der einzelnen Standorte anhand ihrer ‘scores’ im neuen 2-dimensionalen Raum mit fviz_pca_ind():

Code

fviz_pca_ind(pcaA, repel = TRUE)

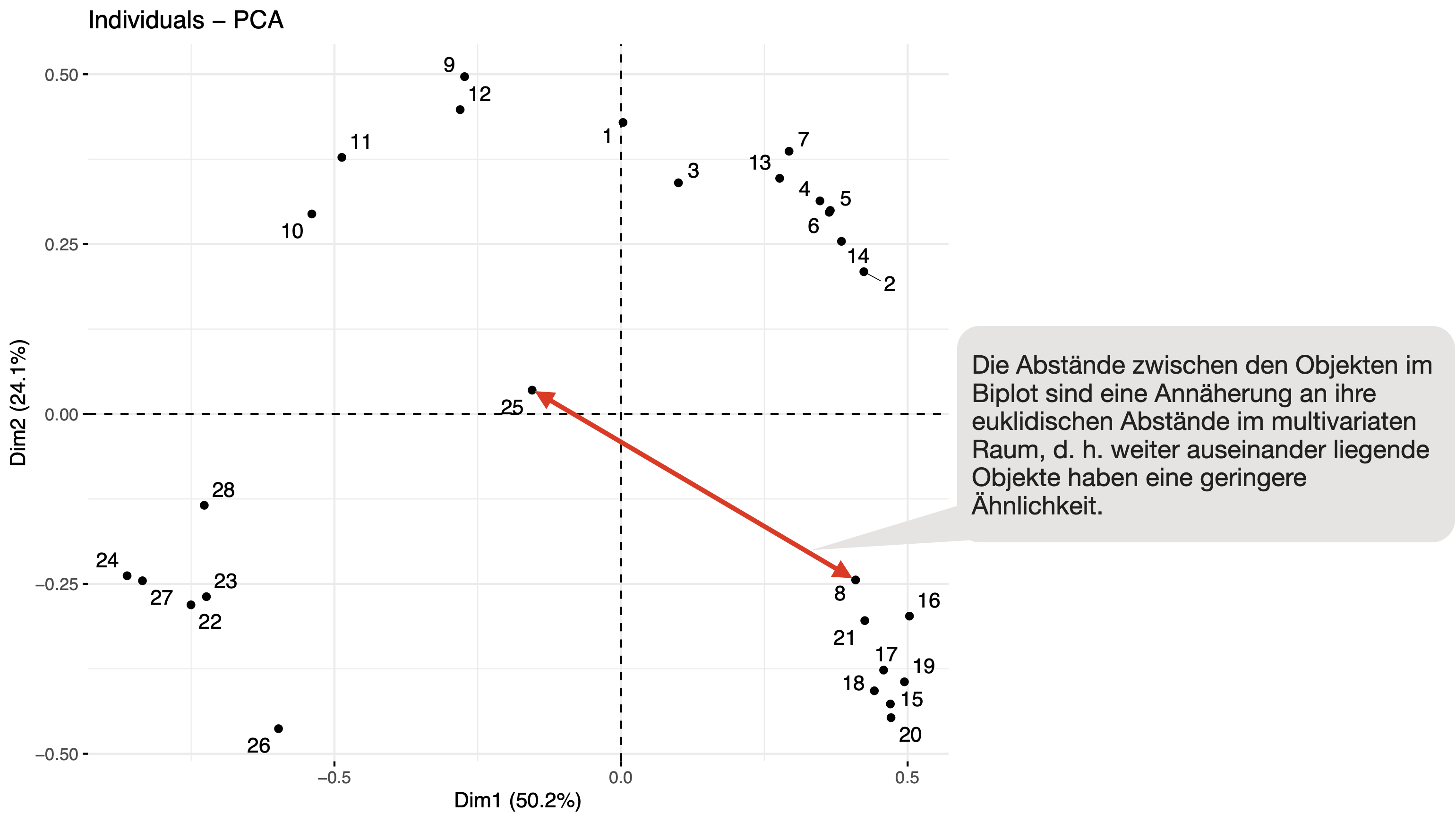
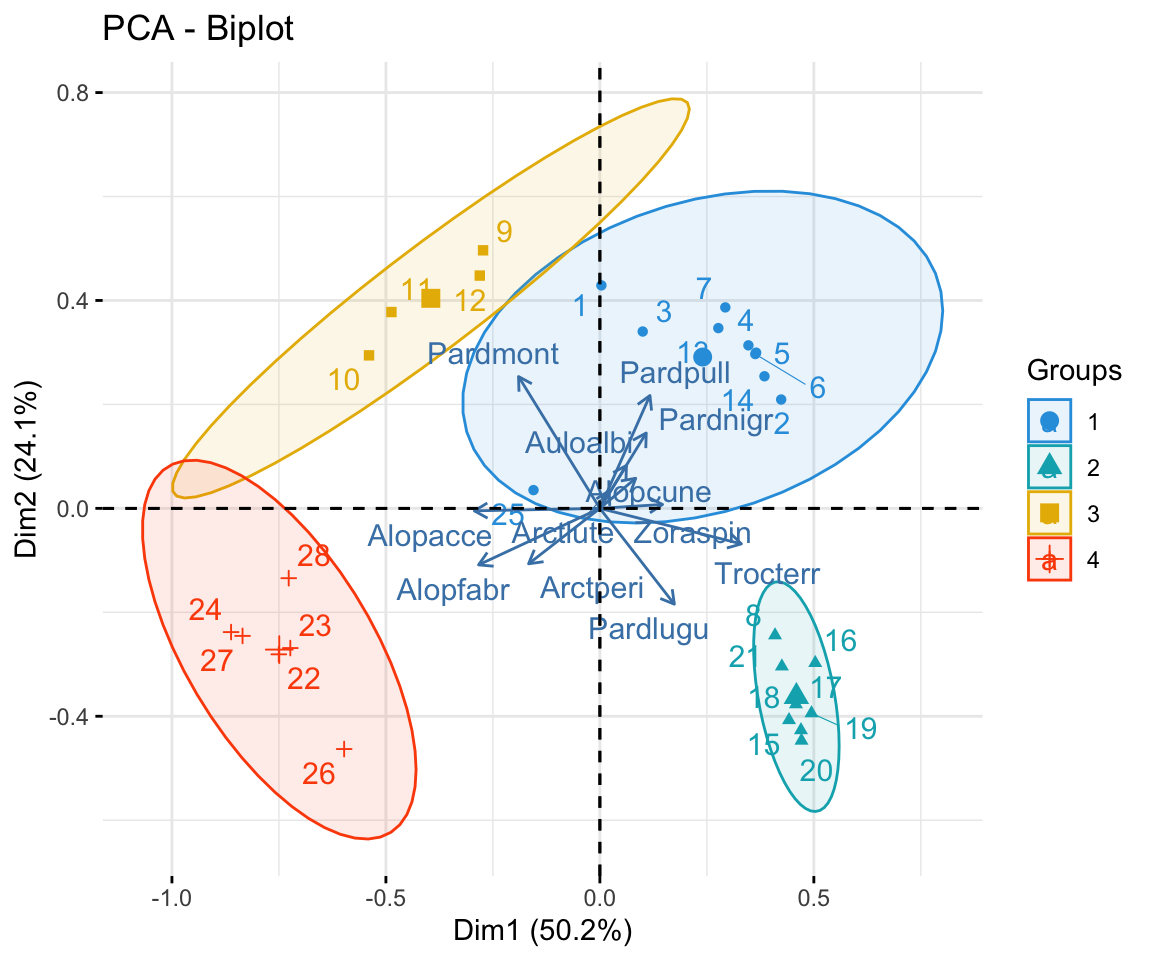
Ergebnisse visualisieren | Biplot

Gemeinsame Darstellung der ‘scores’ und ‘loadings’ im sog. Biplot mit fviz_pca_biplot():

Code

fviz_pca_biplot(pcaA, repel = TRUE,
  col.var = "contrib", 
  gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
  col.ind = "#696969" ) # einheitliche Farbwahl Datenpunkte (Objekte)

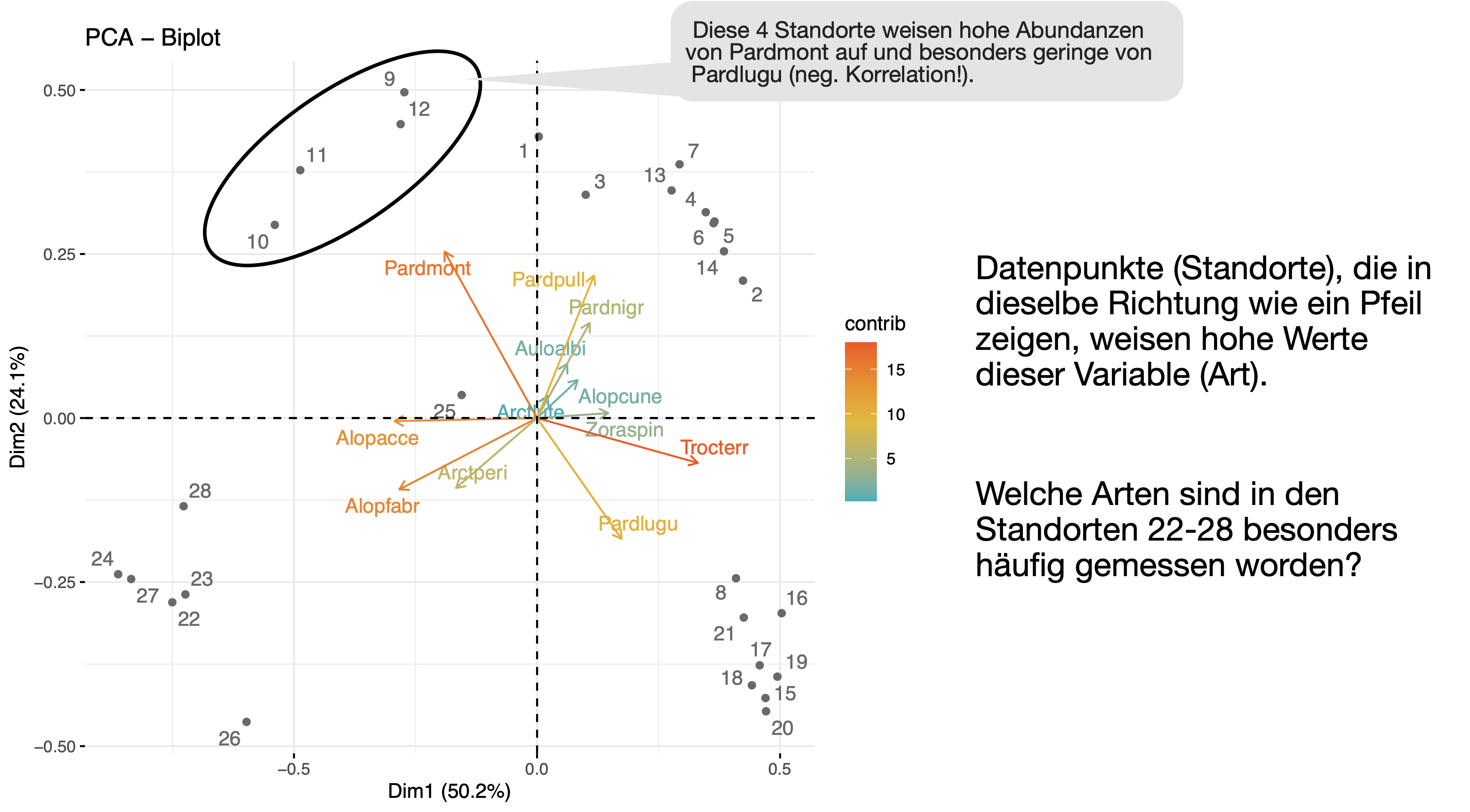
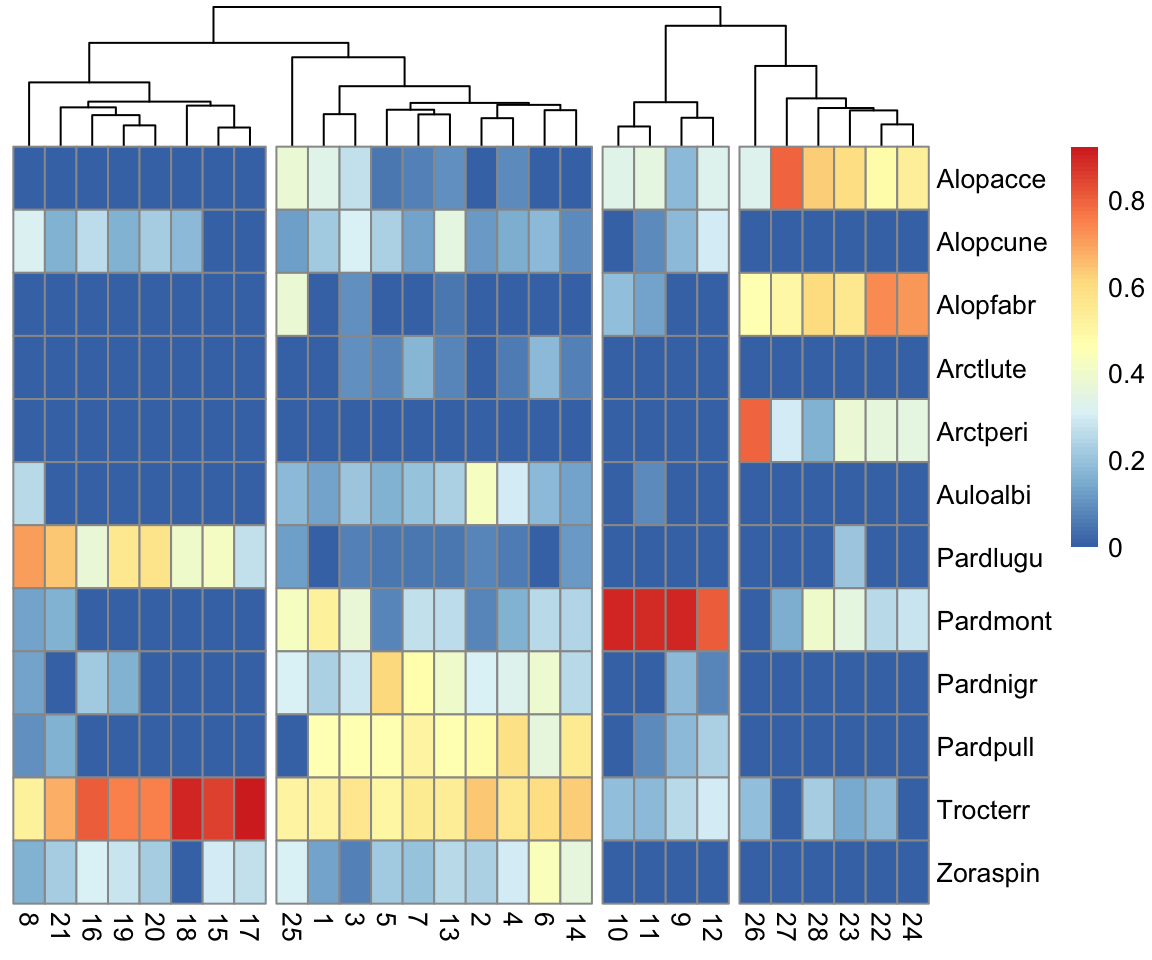
PCA und (hierarchische) Clusteranalyse

Code

pheatmap::pheatmap(t(spiderA_hell), 
  cutree_cols = 4, 
  clustering_method = "average", 
  cluster_rows = FALSE
)

Code

fviz_pca_biplot(pcaA, repel = TRUE,
  col.ind = hc_cluster,
  palette = c("#2E9FDF", "#00AFBB", "#E7B800", "#FC4E07"),
  addEllipses = TRUE, 
  legend.title = "Groups"
)

In Cluster 1 gibt es mehrere schwach dominierende Arten, in Cluster 2 kommt besonders häufig Trocterr und Pardlugu vor. Cluster 3 (Standorte 22-28) weist eine ganz andere Gemeinschaftsstruktur auf mit Alopacce und Alopfabr als dominierende Arten. Die Standorte 9-12 (Cluster 3) werden dominiert von der Art Pardmont.
Zwischen Trocterr und Alopacce bzw. Pardmont und Pardlugu gibt es eine besonders starke negative Korrelation.

Zusammenfassung

Welche Informationen haben wir extrahiert?

Wie die Arten miteinander verwandt sind.
Ob Arten an bestimmten Standorten besonders häufig vorkommen.
Ob es Cluster in den Daten gibt, also Gruppen von Daten, die einander ähnlich sind und welche Arten am stärksten zu den Unterschieden beitragen.

Welche Rolle spielen bei der Gemeinschaftsstruktur die Umweltbedingungen? → Übungsaufgabe

Interpretation bei großen Datensätzen?

Beispiel Genexpressionsmessungen

Code

nci_labs <- NCI60$labs
nci_dat <- NCI60$data
nci_scaled <- scale(nci_dat)
col <- colorRampPalette(c("green", "black", "red"))(255) 

annotation_col = data.frame(nci_labs = nci_labs)
rownames(annotation_col) = rownames(nci_scaled)

pheatmap(t(nci_scaled), cutree_cols = 4, clustering_method = "complete",
  color = col, cluster_rows = FALSE, show_rownames = FALSE,
  annotation_col = annotation_col, fontsize = 7)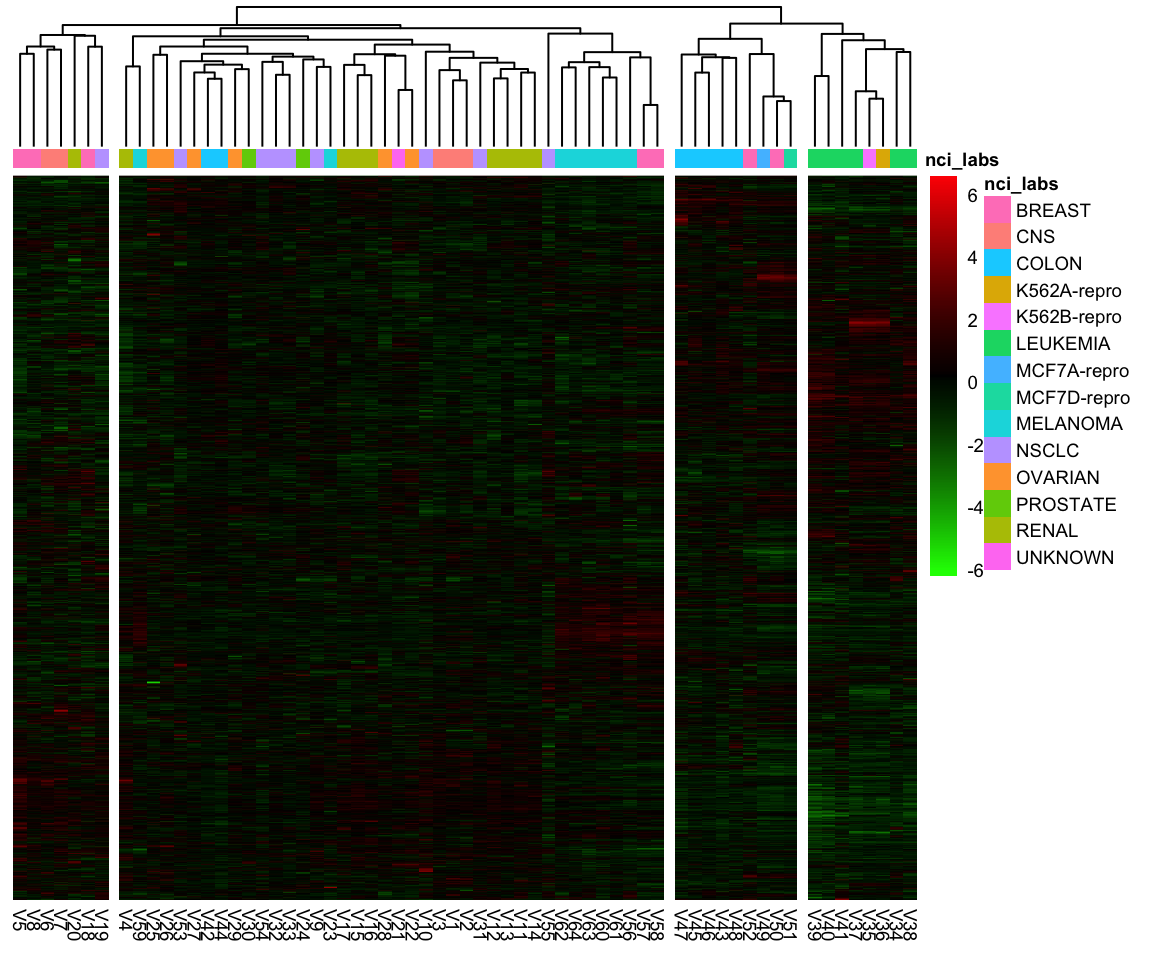

Code

pca_nci <- PCA(nci_dat, scale.unit = TRUE, 
  graph = FALSE)
col <- RColorBrewer::brewer.pal(n = 12, 
  name = "Paired")
col[c(13,14)] <- c("grey25", "grey75")
p <- fviz_pca_ind(pca_nci, col.ind = nci_labs, 
  geom.ind = "point",
  legend.title = "nci_labs",  addEllipses=F)
p + scale_color_manual(values = col) +
  scale_shape_manual(values = 11:24)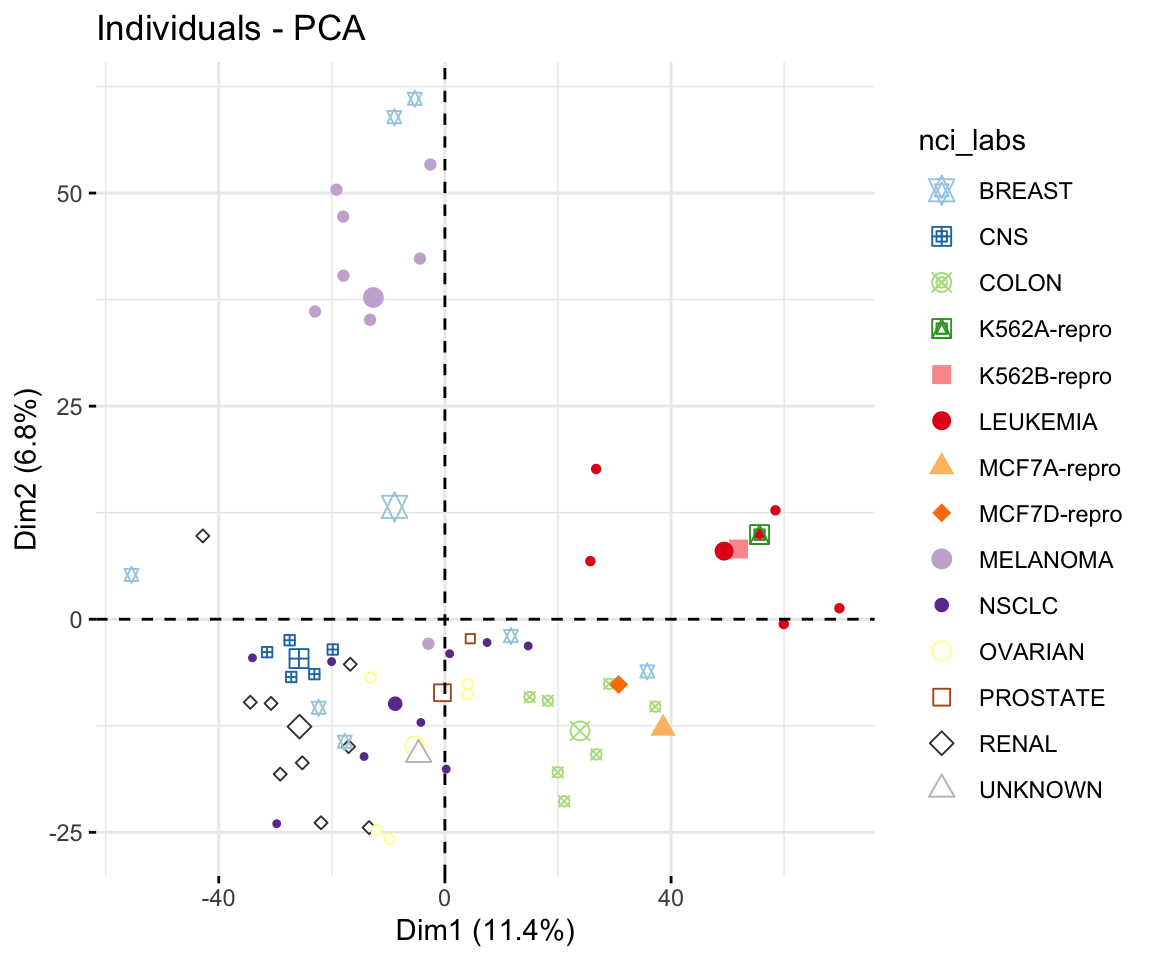

Lassen sich die Krebszelllinien auf Grundlage ihres Genexpressionsprofils in verschiedene Gruppen oder Cluster einordnen?

Your turn …

05:00

PCA von Blüten und Pinguinen

`iris` Datensatz

PCA der vier Blütenmerkmale:
- Sepal.Length , Sepal.Width, Petal.Length, Petal.Width

`penguins` Datensatz (in palmerpenguins)

PCA der vier Körpermerkmale:
- bill_length_mm , bill_depth_mm, flipper_length_mm, body_mass_g

Ziel

Überprüfung, ob sich die Arten anhand einer Kombination der Messgrößen voneinander trennen lassen.
Identifikation, welche Merkmale am stärksten zu den Unterschieden beitragen bzw. miteinander korrelieren.

Foto: Danielle Langlois; Zugriff über Wikipedia(unter CC-BY-SA 3.0 Lizenz).

### Extraktion und Standardisierung der numerischen Variablen
iris_scaled <- scale(iris[ ,1:4])
rownames(iris_scaled) <- iris$Species
head(iris_scaled)

       Sepal.Length Sepal.Width Petal.Length Petal.Width
setosa   -0.8976739  1.01560199    -1.335752   -1.311052
setosa   -1.1392005 -0.13153881    -1.335752   -1.311052
setosa   -1.3807271  0.32731751    -1.392399   -1.311052
setosa   -1.5014904  0.09788935    -1.279104   -1.311052
setosa   -1.0184372  1.24503015    -1.335752   -1.311052
setosa   -0.5353840  1.93331463    -1.165809   -1.048667

### PCA mit den standardisierten Daten und der PCA() Funktion aus dem 
### 'FactoMineR' Paket
iris_pca <- FactoMineR::PCA(iris_scaled, scale.unit = FALSE, graph = FALSE)
summary(iris_pca)


Call:
FactoMineR::PCA(X = iris_scaled, scale.unit = FALSE, graph = FALSE) 


Eigenvalues
                       Dim.1   Dim.2   Dim.3   Dim.4
Variance               2.899   0.908   0.146   0.021
% of var.             72.962  22.851   3.669   0.518
Cumulative % of var.  72.962  95.813  99.482 100.000

Individuals (the 10 first)
                 Dist    Dim.1    ctr   cos2    Dim.2    ctr   cos2    Dim.3
setosa       |  2.311 | -2.257  1.172  0.954 |  0.478  0.168  0.043 | -0.127
setosa.1     |  2.195 | -2.074  0.989  0.893 | -0.672  0.331  0.094 | -0.234
setosa.2     |  2.381 | -2.356  1.277  0.979 | -0.341  0.085  0.020 |  0.044
setosa.3     |  2.370 | -2.292  1.208  0.935 | -0.595  0.260  0.063 |  0.091
setosa.4     |  2.468 | -2.382  1.305  0.932 |  0.645  0.305  0.068 |  0.016
setosa.5     |  2.546 | -2.069  0.984  0.660 |  1.484  1.617  0.340 |  0.027
setosa.6     |  2.459 | -2.436  1.364  0.981 |  0.047  0.002  0.000 |  0.334
setosa.7     |  2.238 | -2.225  1.139  0.988 |  0.222  0.036  0.010 | -0.088
setosa.8     |  2.583 | -2.327  1.245  0.812 | -1.112  0.907  0.185 |  0.145
setosa.9     |  2.241 | -2.177  1.090  0.943 | -0.467  0.160  0.043 | -0.253
                ctr   cos2  
setosa        0.074  0.003 |
setosa.1      0.250  0.011 |
setosa.2      0.009  0.000 |
setosa.3      0.038  0.001 |
setosa.4      0.001  0.000 |
setosa.5      0.003  0.000 |
setosa.6      0.511  0.018 |
setosa.7      0.036  0.002 |
setosa.8      0.096  0.003 |
setosa.9      0.293  0.013 |

Variables
                Dim.1    ctr   cos2    Dim.2    ctr   cos2    Dim.3    ctr
Sepal.Length |  0.887 27.151  0.792 |  0.360 14.244  0.130 | -0.275 51.778
Sepal.Width  | -0.459  7.255  0.212 |  0.880 85.247  0.779 |  0.093  5.972
Petal.Length |  0.988 33.688  0.983 |  0.023  0.060  0.001 |  0.054  2.020
Petal.Width  |  0.962 31.906  0.931 |  0.064  0.448  0.004 |  0.242 40.230
               cos2  
Sepal.Length  0.076 |
Sepal.Width   0.009 |
Petal.Length  0.003 |
Petal.Width   0.059 |

Quiz 2 | Interpretation Screeplot

factoextra::fviz_eig(iris_pca)

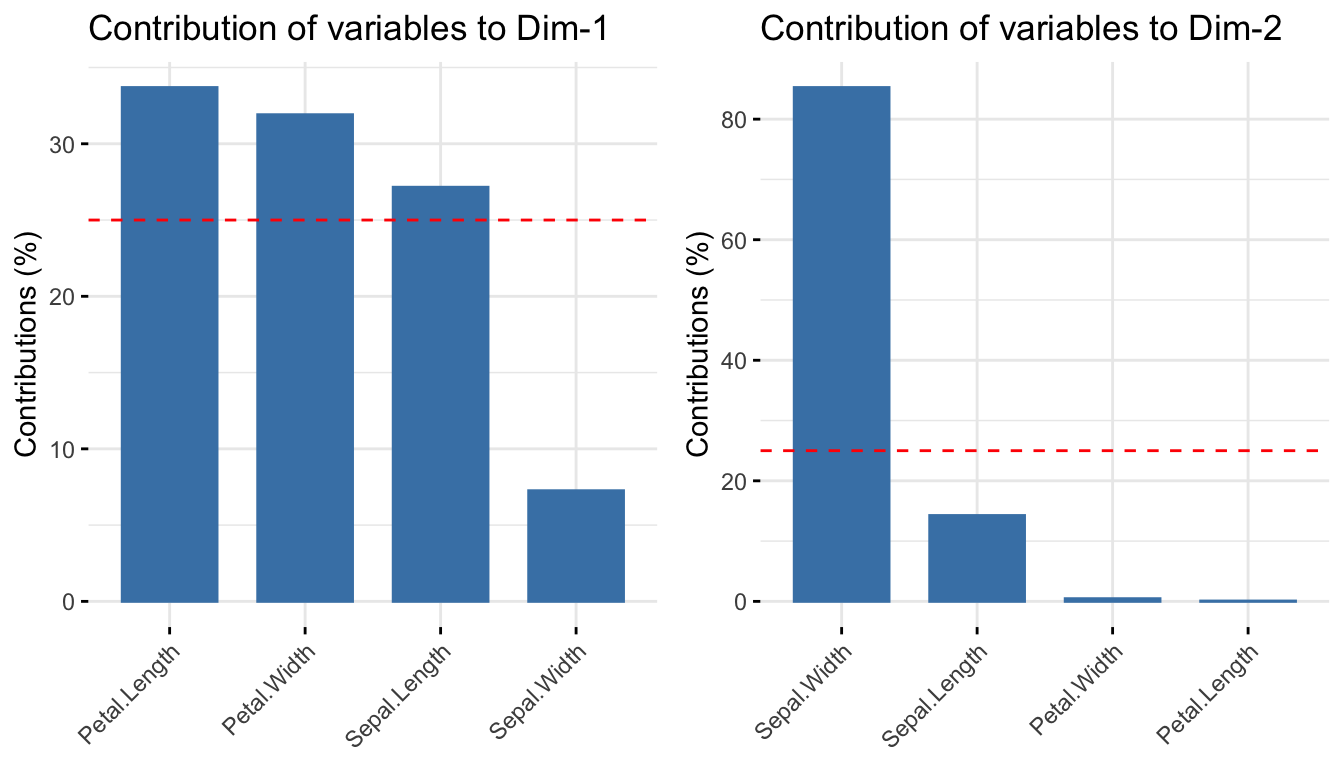
Quiz 3 | Variablenbeiträge zur PCA

Code

p1 <- factoextra::fviz_contrib(iris_pca, choice = "var", 
  axes = 1, top = 10)
p2 <- factoextra::fviz_contrib(iris_pca, choice = "var", 
  axes = 2, top = 10)
gridExtra::grid.arrange(p1, p2, ncol = 2)

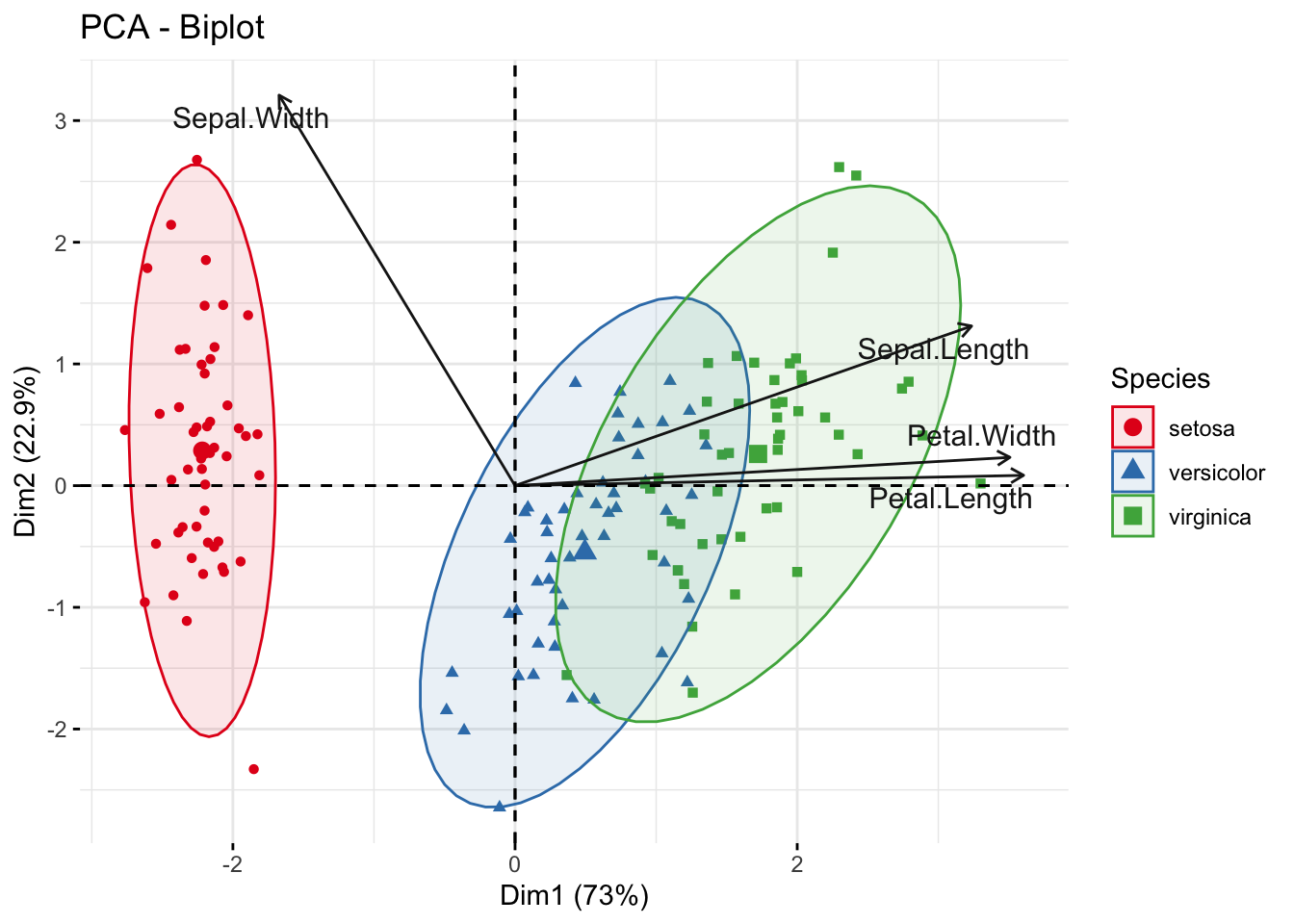
Quiz 4 | Interpretation Biplot 1

Code

factoextra::fviz_pca_biplot(
  X = iris_pca, 
  repel = TRUE,
  col.ind = iris$Species,
  col.var = "grey10",
  palette = RColorBrewer::brewer.pal(3, "Set1"),
  addEllipses = TRUE,
  legend.title = "Species",
  label = "var"
)

Die Pfeile repräsentieren die Variablen: Länge und Richtung zeigen deren Beitrag zu den Dimensionen.
Die Punkte repräsentieren die Individuen (Blüten) und sind nach Art eingefärbt.
Die Ellipsen zeigen die Streuung jeder Art und machen Gruppierungen sichtbar.

Quiz 4 | Interpretation Biplot 2

Quiz 5 | R Code

Lückentext
Demonstration

### Daten laden und modifizieren
data(penguins, package = "palmerpenguins")
penguins <- penguins |> 
  mutate(species_sex = str_c(species, sex, sep = "/")) |> 
  drop_na()

### Extraktion und Standardisierung der numerischen Variablen
penguins_scaled <- scale(penguins[, c(3:6)])
rownames(penguins_scaled) <- penguins$species_sex
head(penguins_scaled)

              bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
Adelie/male       -0.8946955     0.7795590        -1.4246077  -0.5676206
Adelie/female     -0.8215515     0.1194043        -1.0678666  -0.5055254
Adelie/female     -0.6752636     0.4240910        -0.4257325  -1.1885721
Adelie/female     -1.3335592     1.0842457        -0.5684290  -0.9401915
Adelie/male       -0.8581235     1.7444004        -0.7824736  -0.6918109
Adelie/female     -0.9312674     0.3225288        -1.4246077  -0.7228585

### PCA mit den standardisierten Daten und der PCA() Funktion aus dem 
### 'FactoMineR' Paket
penguins_pca <- FactoMineR::PCA(penguins_scaled, scale.unit = FALSE, graph = FALSE)
summary(penguins_pca)


Call:
FactoMineR::PCA(X = penguins_scaled, scale.unit = FALSE, graph = FALSE) 


Eigenvalues
                       Dim.1   Dim.2   Dim.3   Dim.4
Variance               2.737   0.776   0.368   0.108
% of var.             68.634  19.453   9.216   2.697
Cumulative % of var.  68.634  88.087  97.303 100.000

Individuals (the 10 first)
                      Dist    Dim.1    ctr   cos2    Dim.2    ctr   cos2  
Adelie.male       |  1.939 | -1.851  0.376  0.911 |  0.032  0.000  0.000 |
Adelie.female     |  1.444 | -1.314  0.190  0.828 | -0.443  0.076  0.094 |
Adelie.female.1   |  1.493 | -1.375  0.207  0.847 | -0.161  0.010  0.012 |
Adelie.female.2   |  2.040 | -1.882  0.389  0.852 | -0.012  0.000  0.000 |
Adelie.male.1     |  2.207 | -1.917  0.403  0.755 |  0.816  0.258  0.137 |
Adelie.female.3   |  1.877 | -1.770  0.344  0.890 | -0.366  0.052  0.038 |
Adelie.male.2     |  1.678 | -0.817  0.073  0.237 |  0.500  0.097  0.089 |
Adelie.female.4   |  1.930 | -1.796  0.354  0.866 | -0.245  0.023  0.016 |
Adelie.male.3     |  2.436 | -1.953  0.419  0.643 |  0.997  0.385  0.167 |
Adelie.male.4     |  2.654 | -1.567  0.269  0.349 |  0.577  0.129  0.047 |
                   Dim.3    ctr   cos2  
Adelie.male        0.235  0.045  0.015 |
Adelie.female      0.027  0.001  0.000 |
Adelie.female.1   -0.189  0.029  0.016 |
Adelie.female.2    0.628  0.322  0.095 |
Adelie.male.1      0.700  0.400  0.101 |
Adelie.female.3   -0.028  0.001  0.000 |
Adelie.male.2      1.333  1.452  0.631 |
Adelie.female.4   -0.626  0.320  0.105 |
Adelie.male.3      1.039  0.882  0.182 |
Adelie.male.4      2.046  3.421  0.594 |

Variables
                     Dim.1    ctr   cos2    Dim.2    ctr   cos2    Dim.3    ctr
bill_length_mm    |  0.751 20.589  0.565 |  0.529 36.023  0.280 | -0.390 41.280
bill_depth_mm     | -0.660 15.924  0.437 |  0.701 63.389  0.493 |  0.258 18.131
flipper_length_mm |  0.954 33.273  0.913 |  0.005  0.003  0.000 |  0.143  5.574
body_mass_g       |  0.909 30.214  0.829 |  0.067  0.585  0.005 |  0.359 35.015
                    cos2  
bill_length_mm     0.152 |
bill_depth_mm      0.067 |
flipper_length_mm  0.021 |
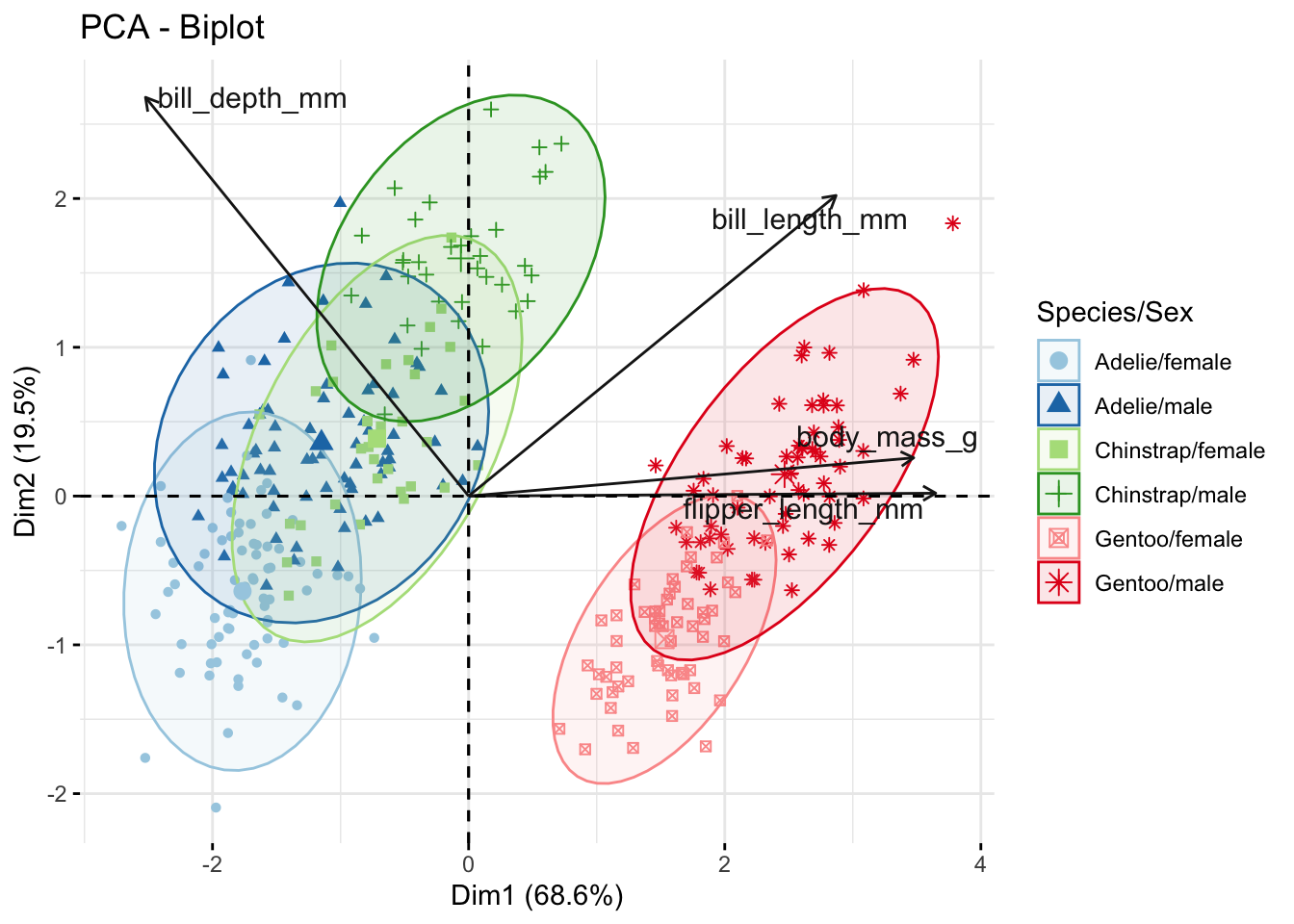
body_mass_g        0.129 |

Quiz 6 | Interpretation Biplot 1

Code

factoextra::fviz_pca_biplot(
  X = penguins_pca, 
  repel = TRUE,
  col.ind = penguins$species_sex,
  col.var = "grey10",
  palette = RColorBrewer::brewer.pal(6, "Paired"),
  addEllipses = TRUE,
  legend.title = "Species/Sex",
  label = "var"
)

Die Pfeile repräsentieren die Variablen: Länge und Richtung zeigen deren Beitrag zu den Dimensionen.
Die Punkte repräsentieren die Individuen (Pinguine) und sind nach Art und Geschlecht eingefärbt.
Die Ellipsen zeigen die Streuung jeder Art/Geschlecht-Kombination und machen Gruppierungen sichtbar.

Quiz 6 | Interpretation Biplot 2

Übungen

Übungswoche 7

Gemeinschaftsstruktur von Wolfsspinnen und mögliche Umwelteinflüsse (Teil 2)

Vorbereitung @home

Univariate Analyse der Diversität
- Datenexploration
PCA der Wolfspinnengemeinschaft
- Wiederholung der PCA-Methode (inkl. dem R Code) und die Ergebnisse zur Spinnengemeinschaft aus der Vorlesung.
Beantworten Sie vor der sechsten Übungsstunde die Fragen zur PCA im Moodle-Quiz.

Fragen..??

Total konfus?

Buchkapitel zum Nachlesen

The R Book von M.J. Crawley:
- Kapitel 25.1 Principal components analysis
Experimental Design and Data Analysis for Biologists von G.P. Quinn & M.J. Keough:
- Kapitel 17 Principal components and correspondence analysis
Weitere empfehlenswerte Bücher:
- P. Legendre & L. Legendre (2012): Numerical Ecology, Elsevier Offizielle Webseite
- Borcard, Gillet & Legendre (2011): Numerical Ecology with R, Springer Offizielle Webseite
- A. Kassambara (2017): Practical Guide To Principal Component Methods in R. Weblink
Online-Tutorial von A. Kassambara: PCA - Principal Component Analysis Essentials

Cheetsheets

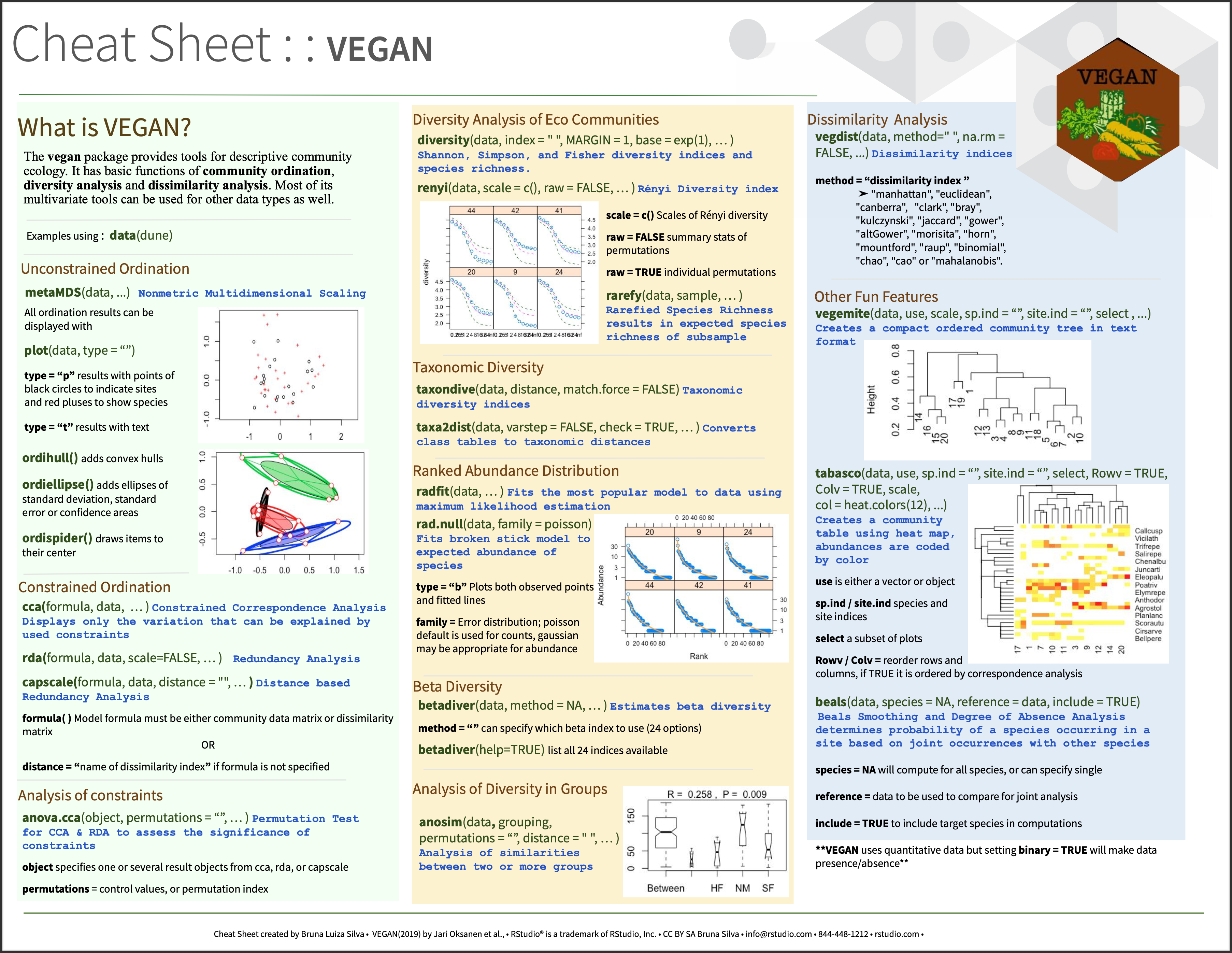
Empfehlenswert ist auch das Cheatsheet des ‘vegan’ Pakets: https://github.com/rstudio/cheatsheets/blob/main/vegan.pdf

Total gelangweilt?

Dann testen Sie doch Ihr Wissen in folgendem Abschlussquiz…

Abschlussquiz

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de

Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.

Unsupervised Learning: Hauptkomponentenanalyse (PCA)

Lernziele

Am Ende dieser VL- und Übungseinheit werden Sie

Principal Component Analysis (PCA)

Ordinationstechniken

Beispiele für Ordinationsverfahren

PCA - Hauptkomponentenanalyse

PCA - “Geometrischer” Ansatz | 1

PCA - “Geometrischer” Ansatz | 2

PCA - “Geometrischer” Ansatz | 3

PCA - “Geometrischer” Ansatz | 4

PCA - Mathematischer Ansatz

Berechnung der PC ‘Scores’

Matrix Z:

(Zentrierte) Datenmatrix X:

Matrix U der k Eigenvektoren:

Durchführung in R

Manuelle Berechnung (in R)

Für ganz interessierte…

PCA in R

Output extrahieren

Anteil der erklärten Varianz

Wie viele Komponenten (PCs)?

Beiträge der Variablen zu den PCs

Ergebnisse visualisieren | Variablen

Ergebnisse visualisieren | Objekte

Ergebnisse visualisieren | Biplot

PCA und (hierarchische) Clusteranalyse

Zusammenfassung

Welche Informationen haben wir extrahiert?

Interpretation bei großen Datensätzen?

Beispiel Genexpressionsmessungen

Your turn …

PCA von Blüten und Pinguinen

iris Datensatz

penguins Datensatz (in palmerpenguins)

Ziel

Quiz 1 | R Code

Quiz 2 | Interpretation Screeplot

Quiz 3 | Variablenbeiträge zur PCA

Quiz 4 | Interpretation Biplot 1

Quiz 4 | Interpretation Biplot 2

Quiz 5 | R Code

Quiz 6 | Interpretation Biplot 1

Quiz 6 | Interpretation Biplot 2

Übungen

Übungswoche 7

Fragen..??

Total konfus?

Buchkapitel zum Nachlesen

Cheetsheets

Total gelangweilt?

Abschlussquiz

`iris` Datensatz

`penguins` Datensatz (in palmerpenguins)