Unsupervised Learning: Clusteranalyse und PCA

DS3 - Explorative Datenanalyse & Data Mining

Saskia Otto

Universität Hamburg, IMF

Wintersemester 2023/2024

Lernziele

Am Ende dieser VL- und Übungseinheit werden Sie

einen groben Überblick über Analysetechniken zu multivariaten Datensätzen in der Biologie haben.
wissen, was eine Assoziationsmatrix ist und wie diese berechnet wird.
die Grundprinzipien der hierarchischen Clusteranalyse verstanden haben.
in der Lage sein, den geeigneten Clustering-Algorithmus für verschiedene Datensätze und Fragestellungen auszuwählen.
die Grundlagen der Hauptkomponentenanalyse (PCA) verstanden haben, einschließlich des Ziels, die Dimensionalität von Daten zu reduzieren und die wichtigsten Informationen zu extrahieren.
in der Lage sein, die Unterschiede und Gemeinsamkeiten zwischen Clusteranalyse und PCA zu verstehen und zu erklären.

Analysen multivariater Daten

Biologische Daten sind oft multivariat… | 1

Biologische Daten sind oft multivariat… | 2

Mehrere (Antwort-)Variablen (Abundanzen von Arten, Umweltvariablen, Messungen von biologischen Merkmalen (‘traits’), Gensequenzen, …)
Mehrere Objekte (z. B. Standorte, Zeit, Individuen, experimentelle Einheiten,…)

Beispiele multivariater Daten | 1

Genomdaten

Microarray-Daten, die aus 6.830 Genexpressionsmessungen (Variablen: kontinuierlich) an 64 Krebszelllinien bestehen.
Mögliche Fragestellung: Lassen sich die Krebszelllinien auf Grundlage ihres Genexpressionsprofils in verschiedene Gruppen oder Cluster einordnen?
- → Schwierige Frage, weil es sehr viele Genexpressionsmessungen pro Zelllinie gibt, was es schwierig macht, die Daten zu visualisieren!

Bildquelle: James et al. (2013): Introduction to Statistical Learning

Beispiele multivariater Daten | 2

Physiologische Daten

Fettsäurenzusammensetzung des Blubbers (Variablen: kontinuierlich) bei 89 Schweinswalen.
Mögliche Fragestellung: Können wir Gruppen von Individuen mit unterschiedlichen Ernährungsgewohnheiten identifizieren?

Bildquelle Schweinswal: Wikipedia (von Ecomare/Salko de Wolf Den Hoorn Texel), CC BY-SA 4.0

Beispiele multivariater Daten | 3

Trait-Daten

Merkmale oder traits (Variablen: quantitativ/ qualitativ) verschiedener Fisch- oder Zooplanktonarten.
Mögliche Fragestellung: Lassen sich die Arten in funktionelle Gruppen zusammenlegen?

Fischdaten/-abbildung aus: Beukhof et al. (2019): A trait collection of marine fish species from North Atlantic and Northeast Pacific continental shelf seas.

Beispiele multivariater Daten | 4

Abundanzsdaten einer biol. Gemeinschaft

Abundanzen von Wolfspinnen (und Umweltparameter) (Variablen: diskret/kontinuerlich), die an verschiedenen Standorten eines Dünenengebiets in den Niederlande gemessen wurden.
→ Problematisch bei Abundanzdaten: enthalten oft viele Nullen!
Mögliche Fragestellungen:

Bildquelle oben rechts: Wikipedia (von Casliber-Eigenes Werk), CC BY-SA 3.0

Wie können wir multivariate Daten analysieren?

Indizes berechnen

Diversitätsindizes

Diversitätsindizes sind quantitative Maße, die verwendet werden, um die biologische Vielfalt oder Diversität in einem bestimmten Ökosystem, einer Population oder einer Gemeinschaft zu bewerten.
Je nach Index wird die Anzahl der verschiedenen Arten sowie deren Häufigkeit, Abundanz bzw. Verteilung, deren Traits und/oder Phylogenie berücksichtigt.
Unterscheidet in
- taxonomische Diversität → hier ist das R Paket vegan nützlich
- funktionelle Diversität → R Paket mFD
- phylogenetische Diversität → R Pakete ape und picante

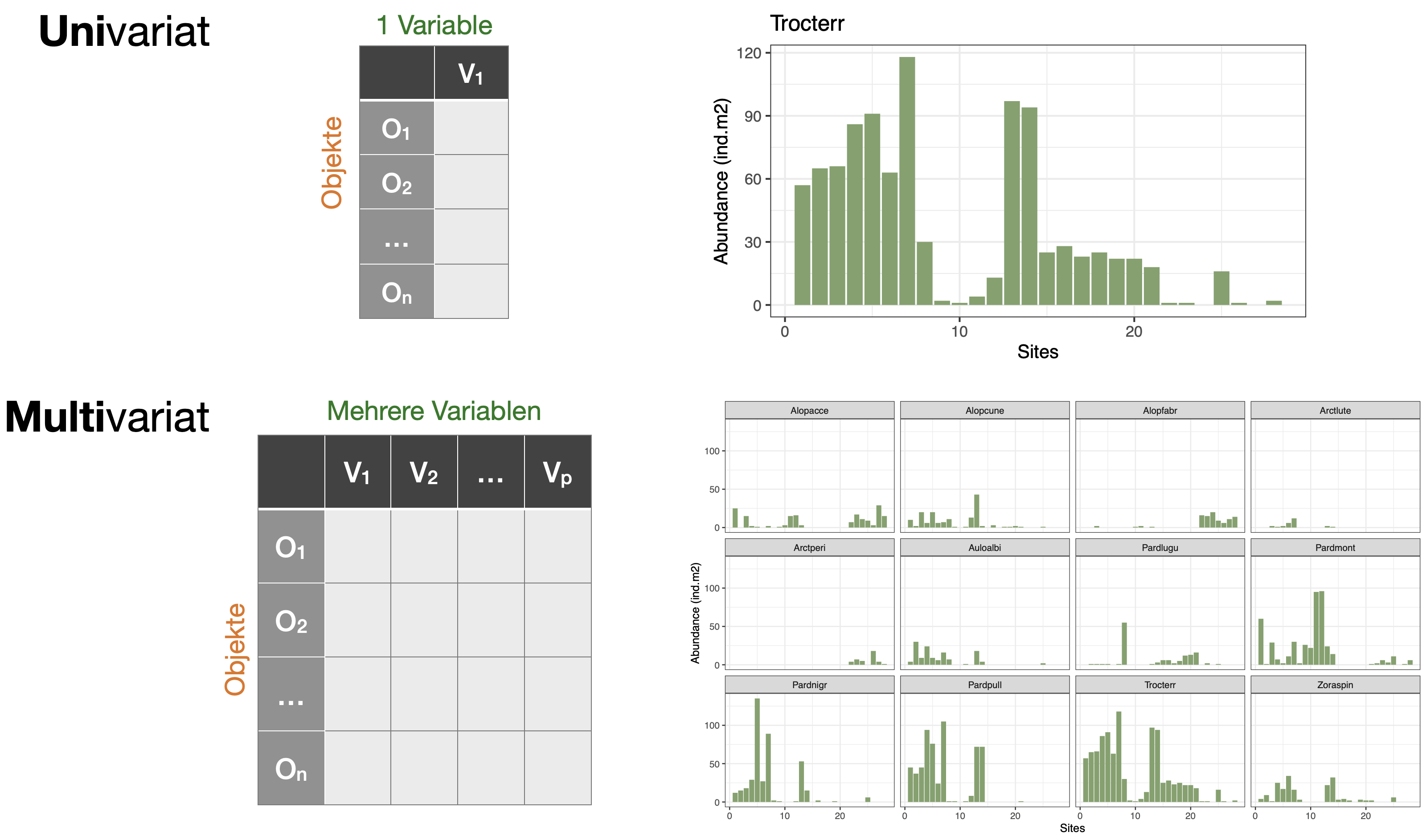
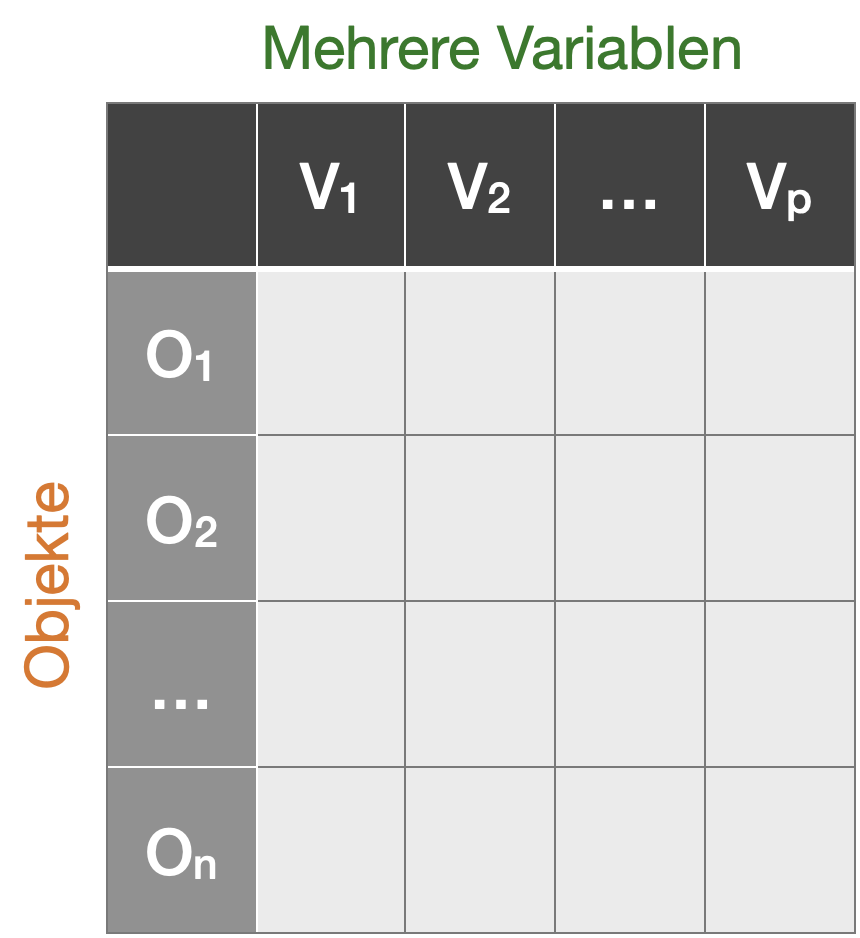
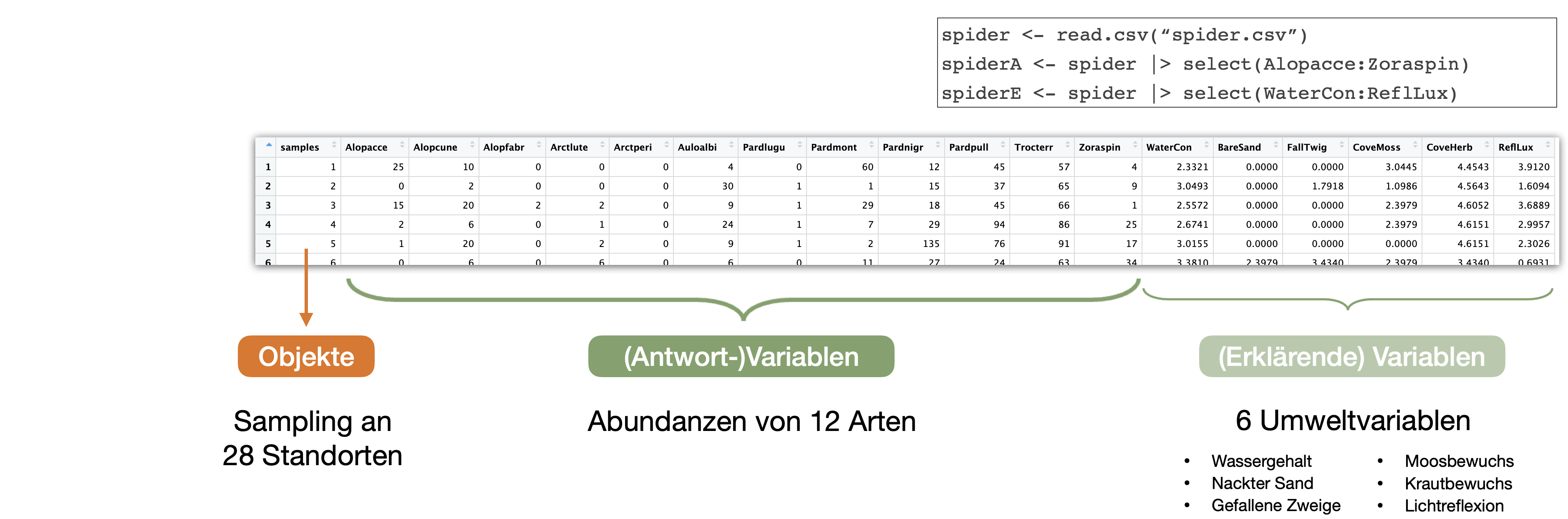
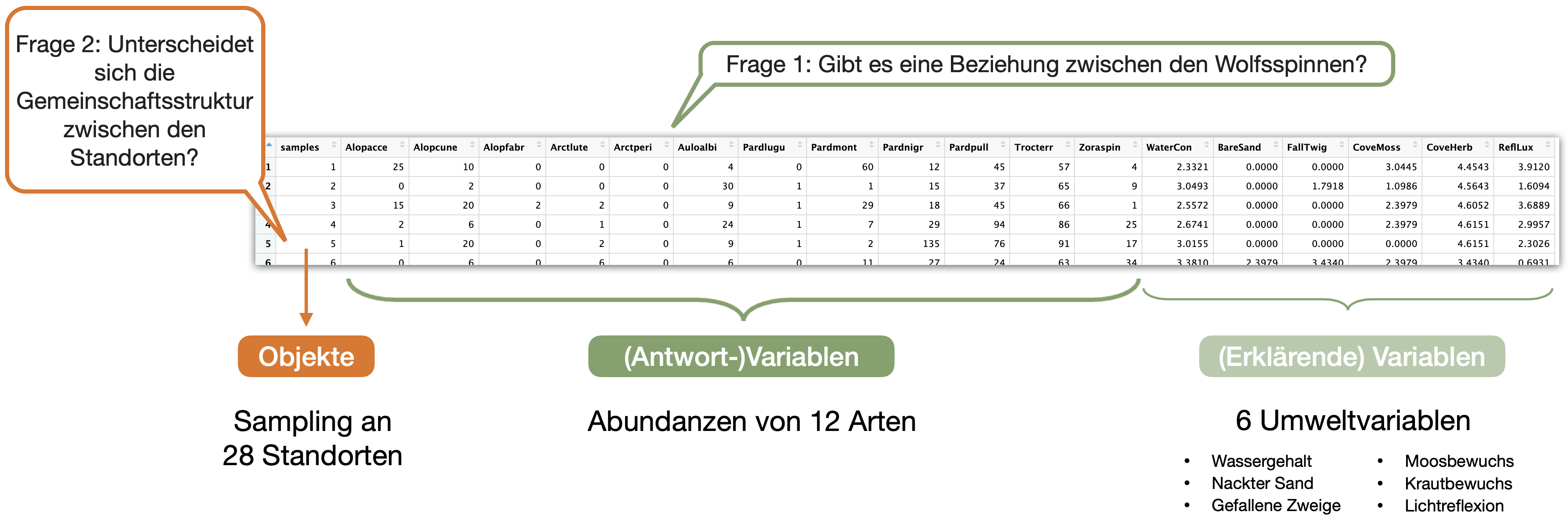
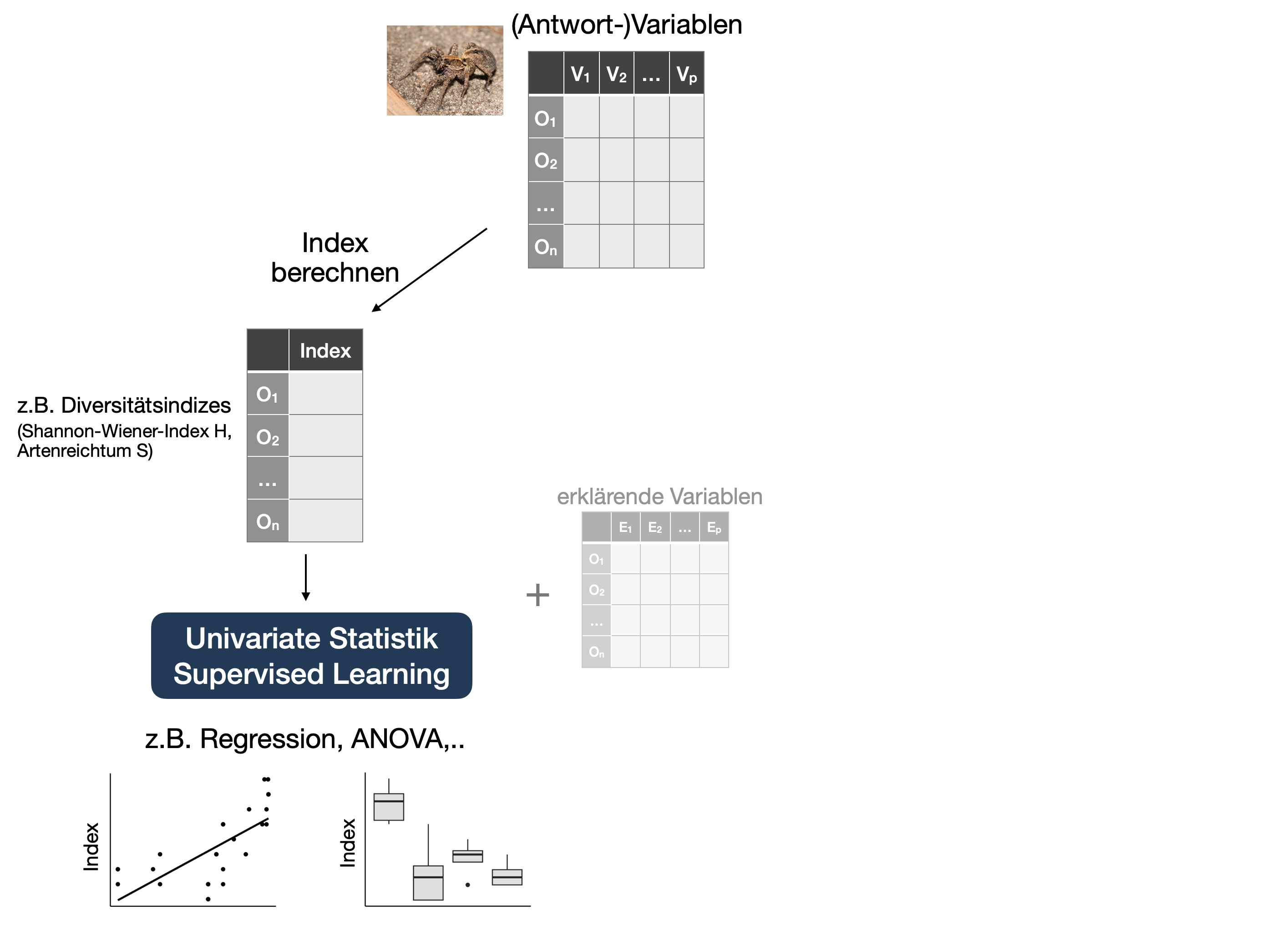
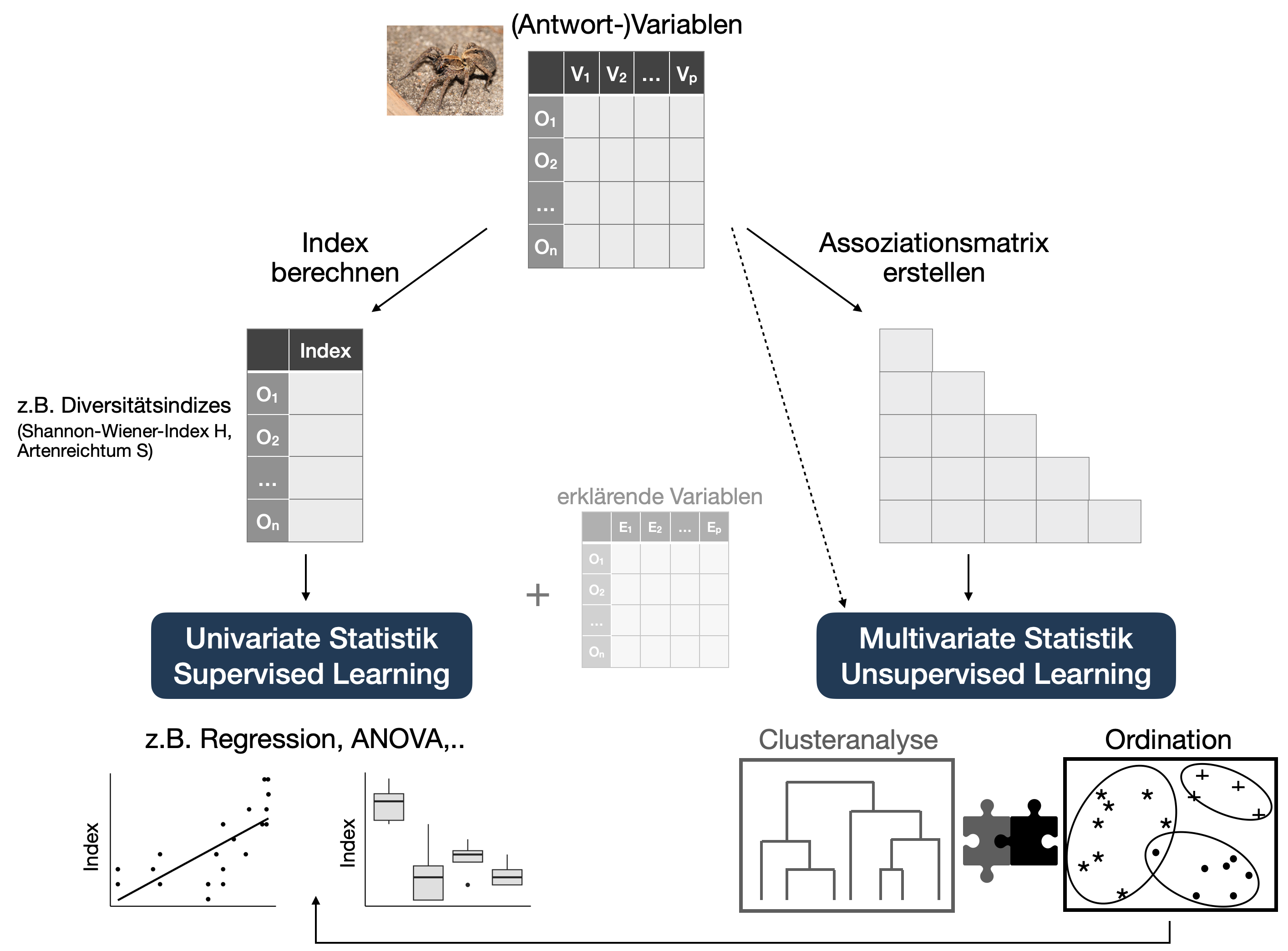
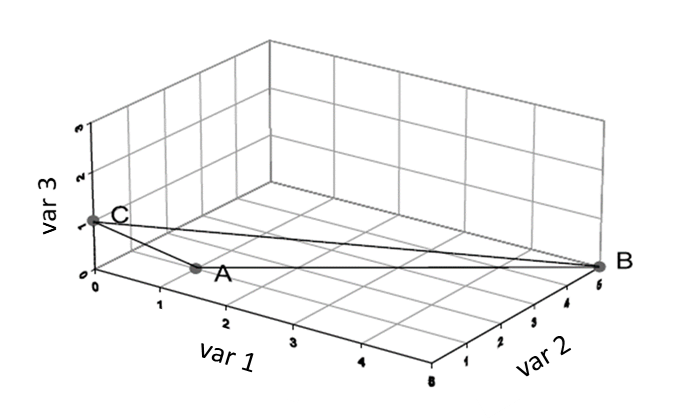
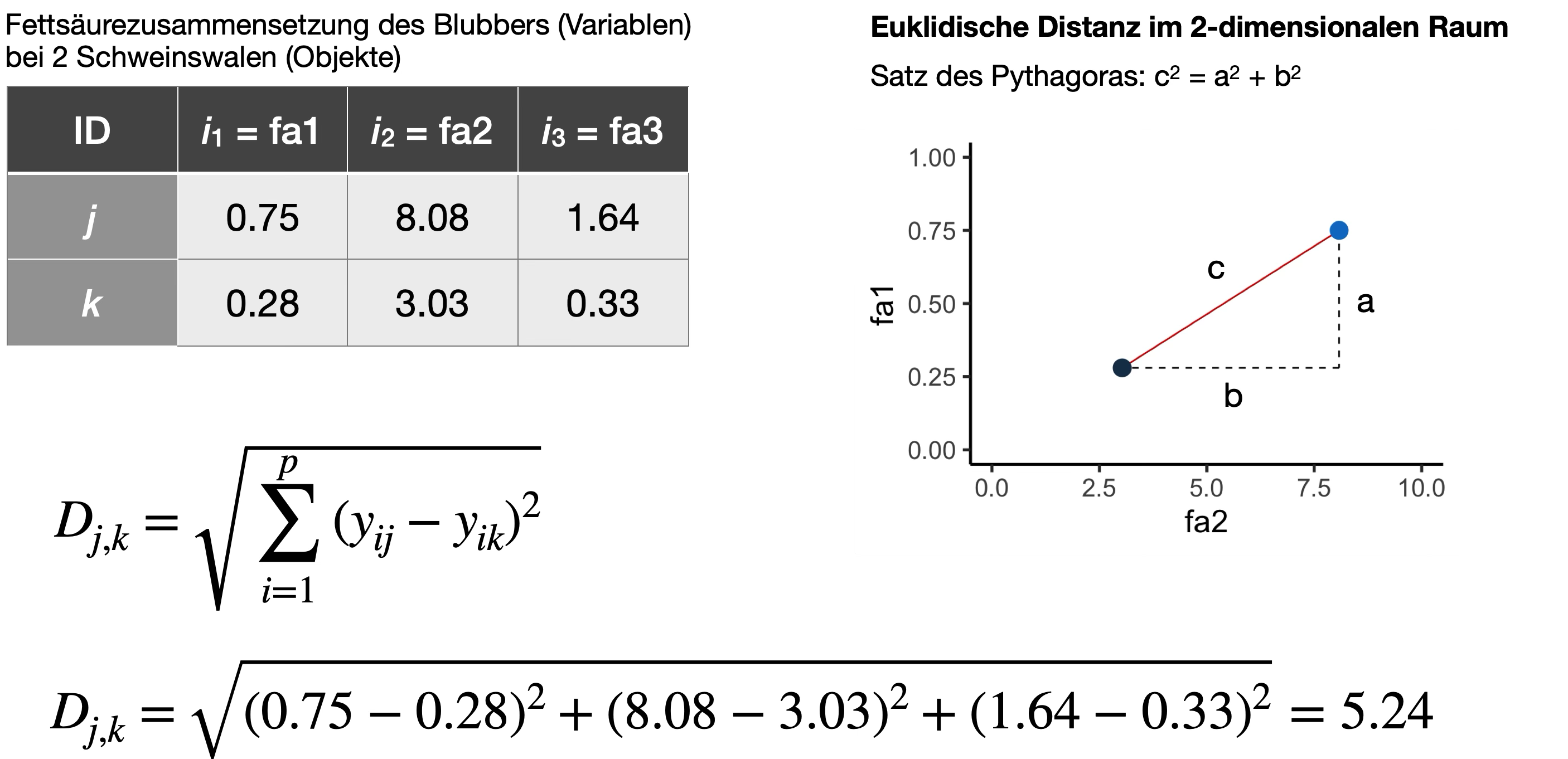
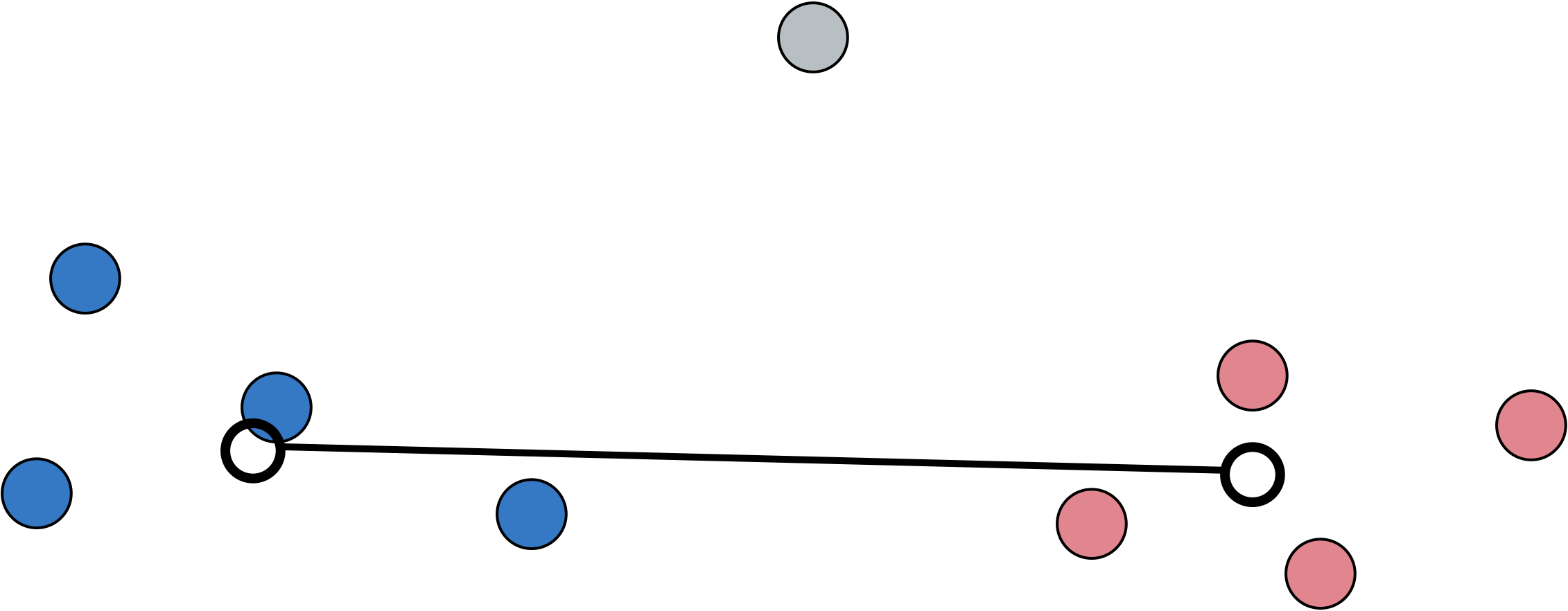
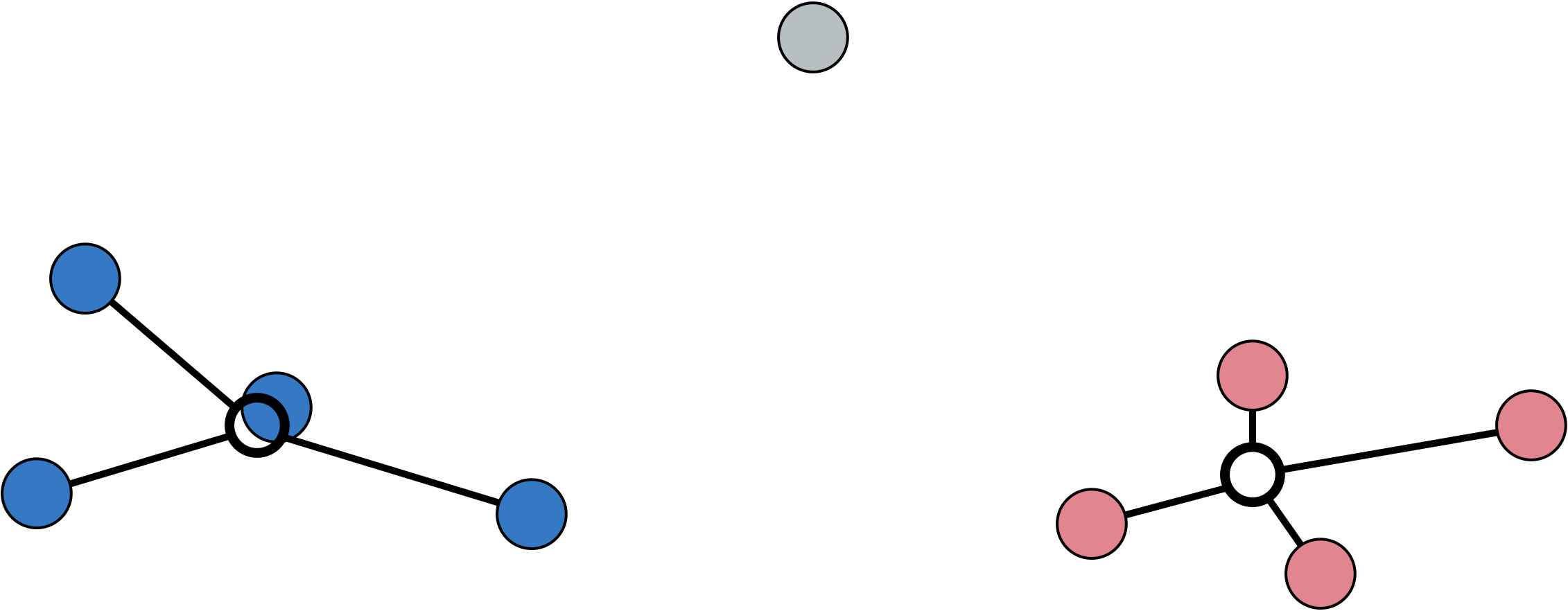
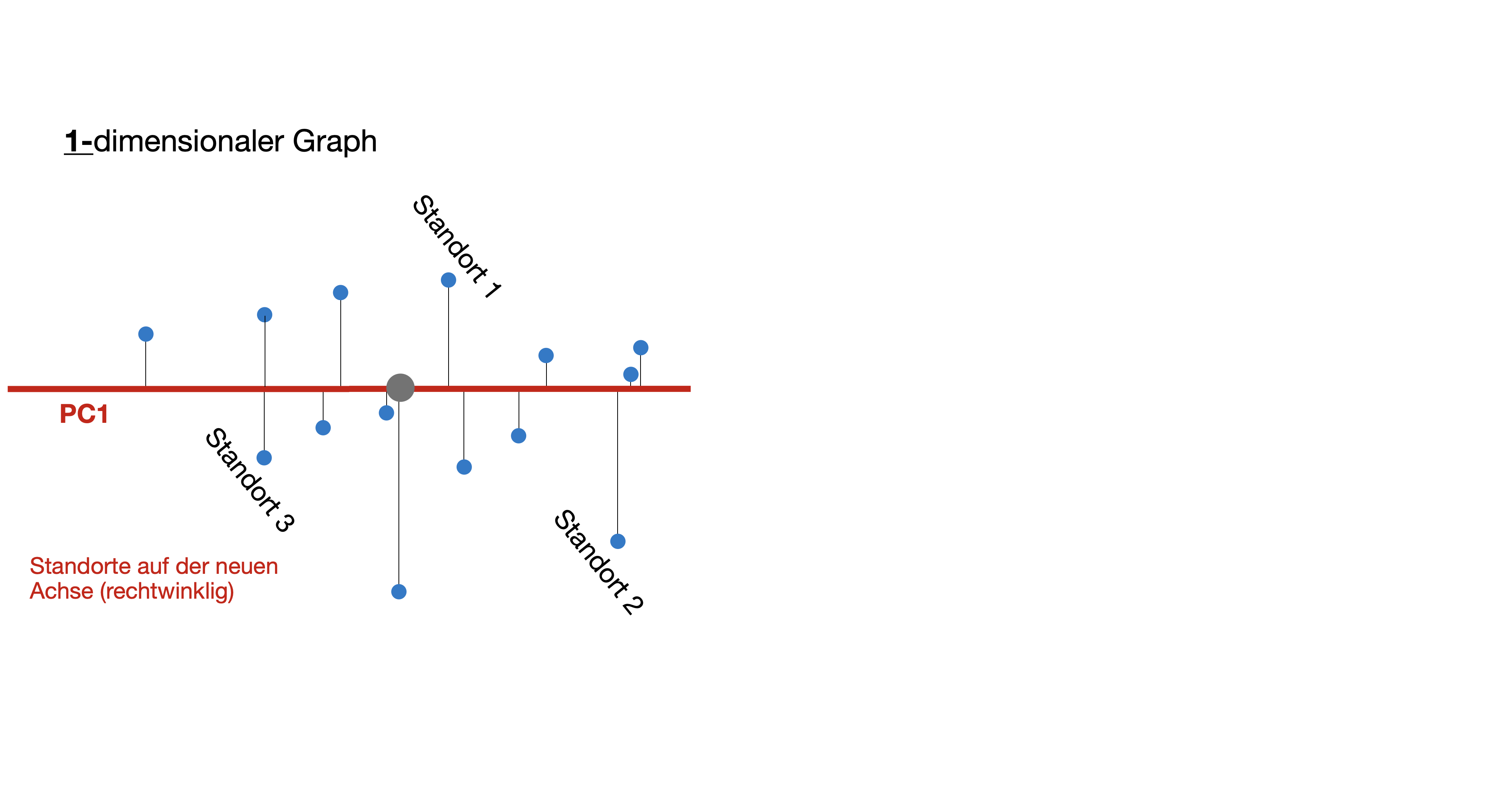
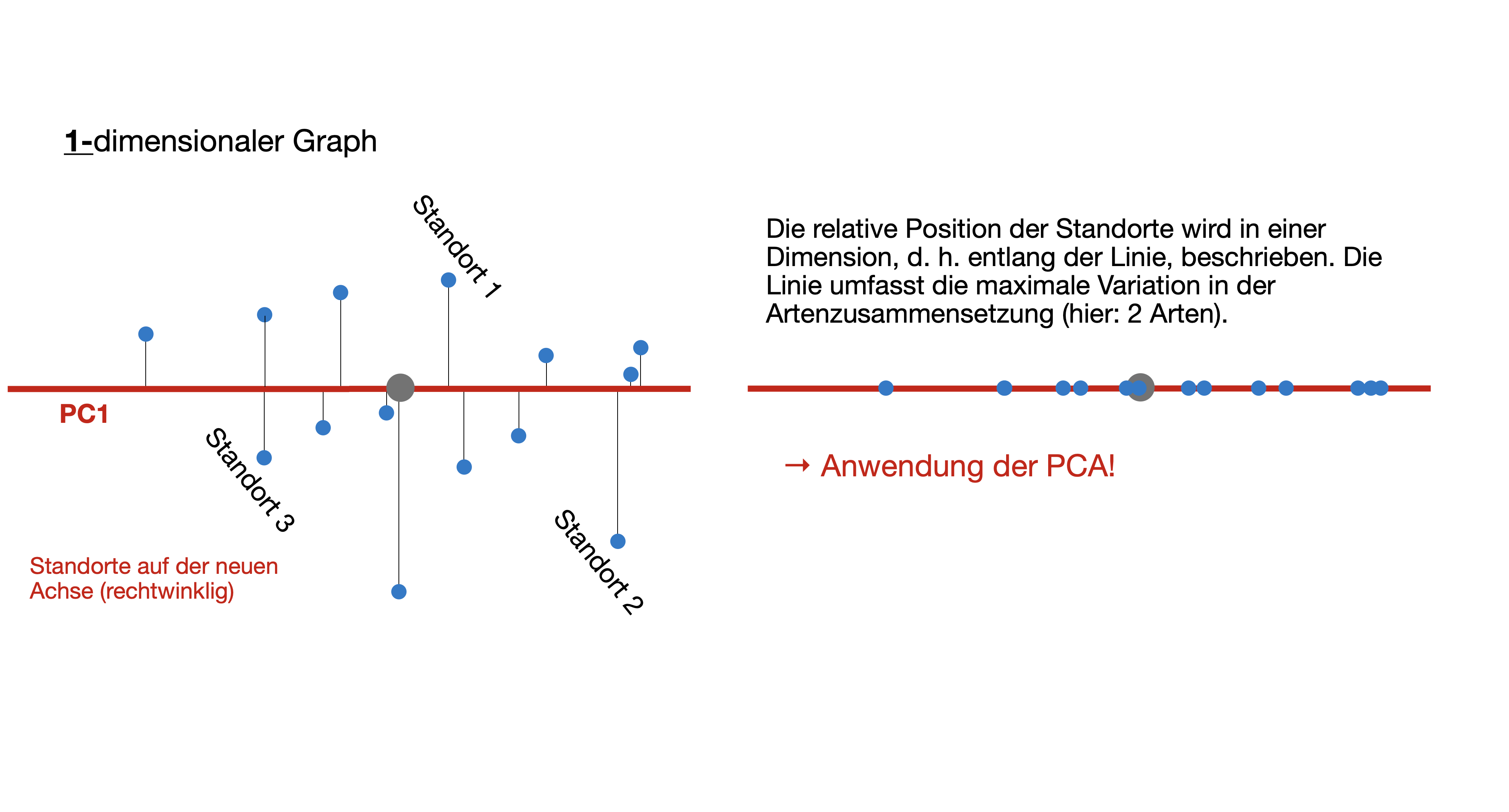
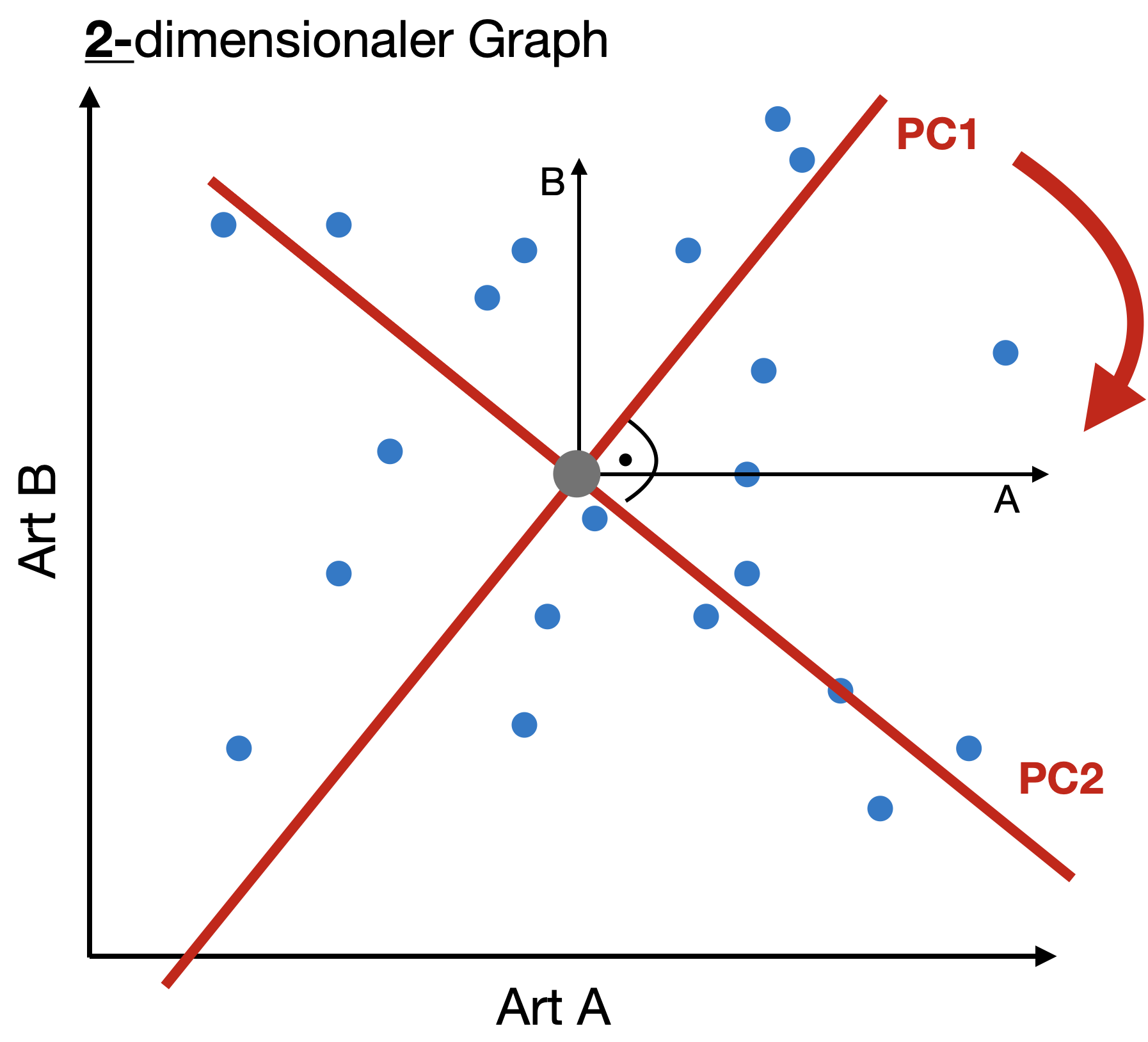
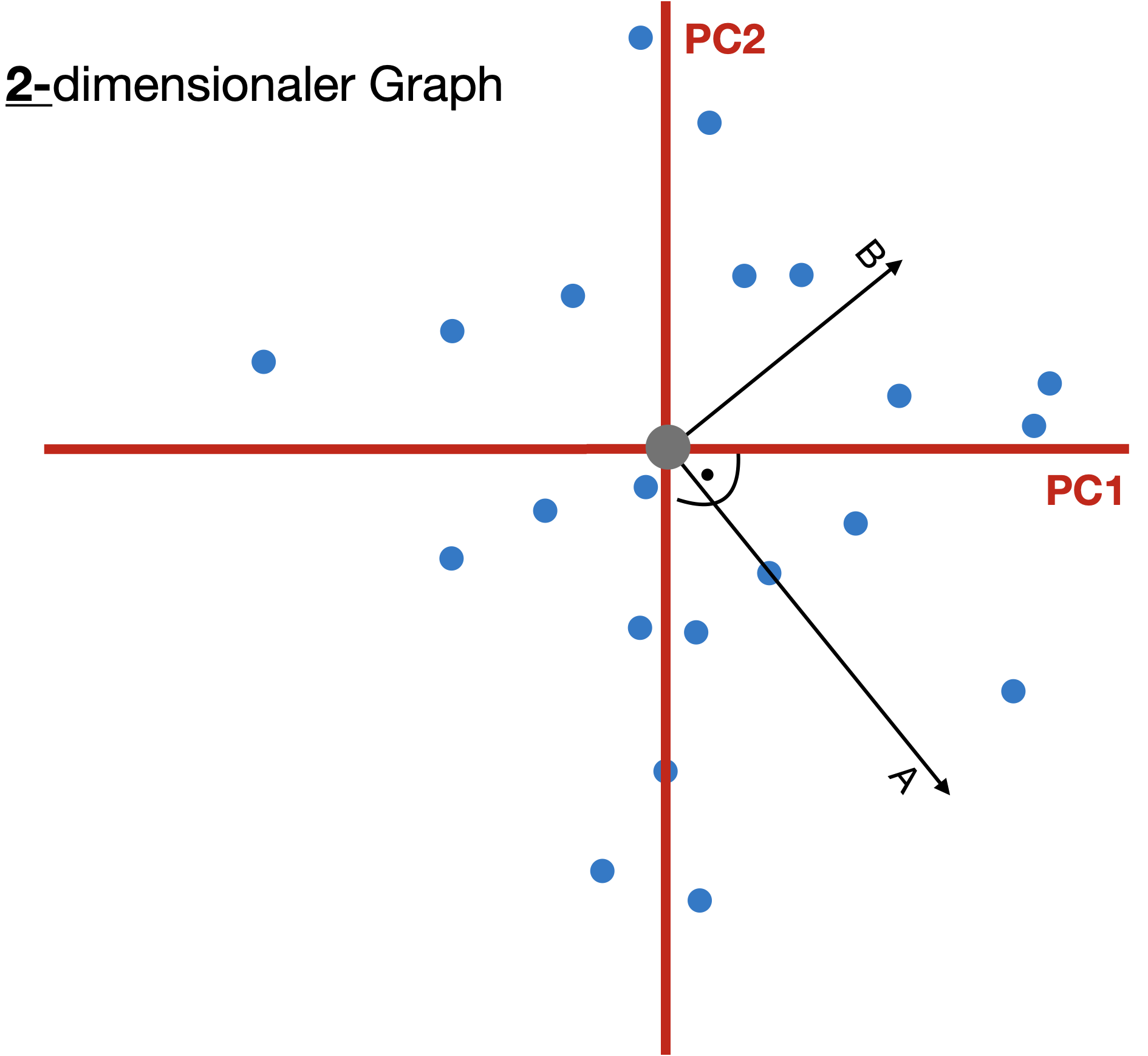
Artenreichtum S und Shannon Index H mit 'vegan' berechnen:

spiderA |> transmute(samples = 1:28,
    S = vegan::specnumber(x = spiderA),
    H =  vegan::diversity(x = spiderA, index = "shannon") ) |>
  arrange(desc(S), desc(H))

   samples  S         H
1       13 11 1.8742271
2        3 11 1.8732193
3        7 10 1.7221199
4        4 10 1.6520490
5        5 10 1.5403056
6       25  9 1.9276654
7       14  9 1.5284480
8        6  8 1.7591828
9        1  8 1.7309509
10       2  8 1.5204418
11       8  8 1.3896573
12      11  7 0.7440770
13      23  6 1.4848760
14      21  6 1.1565256
15      12  6 1.1410240
16       9  6 0.7752108
17      28  5 1.2769439
18      22  5 1.2373886
19      16  5 1.1035352
20      19  5 1.0708014
21      24  4 1.1601124
22      20  4 0.9938215
23      26  4 0.9724515
24      27  4 0.9272491
25      10  4 0.6551416
26      15  3 0.7464108
27      18  3 0.5785328
28      17  3 0.5221718

→ Messung #13 weist die höchste Artenzahl auf (12) und Messung #25 die höchste Shannon Diversität (bei der auch die relative Häufigkeit berücksichtigt wird.)

Assoziationsmatrix

2 Typen von Assoziationsmatrix

Q-Mode | Euklidische Distanz 1

Vektorieller Abstand zwischen Punkten in einem p (Anzahl der Variablen) dimensionalen Raum, dem euklidischen Raum.

Q-Mode | Euklidische Distanz 2

Blubber Beispiel

Q-Mode | Euklidische Distanz 3

Hängt stark vom Wert der Variablen ab, und dieser Wert wird durch die Skala jeder Variablen beeinflusst. Wird beispielsweise g in mg umgewandelt, so wird der Beitrag dieser Variablen zum euklidischen Abstand mit 1000 multipliziert. Wenn die Variablen unterschiedliche Einheiten haben, müssen sie daher alle standardisiert werden (z-Transformation):
- \frac{x-\hat{x}}{s} → in R Funktion scale(x, center = TRUE, scale = TRUE)

= symmetrischer Koeffizient: betrachtet 0 als genauso aussagekräftig wie jeden anderen Wert. Beispiel Temperatur:
- Standort₁ = 0 °C vs. Standort₂ = 15 °C → Es ist kälter bei Standort₁ → unterschiedlich
- Standort₁ = 0 °C vs. Standort₂ = 0.2 °C → Es ist bei beiden Standorten kalt → gleich

Anwendung in R: Umweltdaten im spider Datensatz

# Standardisierung
spiderE_scaled <- scale(x = spiderE)
# Und nun die Euklidische Distanz
spiderE_edist <- dist(spiderE_scaled, method = "euclidean") # default

Q-Mode | Artvorkommen

Das Problem der doppelten Nullen!

Bei Abundanz- oder Biomassedaten von Arten:
- Standort₁ = 10 vs. Standort₂ = 10 → die Standorte bieten ähnliche Umweltbedingungen für das Überleben der Art → ähnlich
- Standort₁ = 0 vs. Standort₂ = 0 → bieten sie ähnlich ungünstige Bedingungen für das Überleben der Art? → ähnlich? Nicht unbedingt…

Das Fehlen einer Art an zwei Standorten bedeutet nicht direkt eine Ähnlichkeit zwischen diesen Standorten, da dieses doppelte Fehlen verschiedene Gründe haben kann.
Die Anzahl der doppelten Abwesenheiten in einer Artenmatrix hängt von der Anzahl der Arten im Datensatz ab und nimmt mit der Anzahl der seltenen Arten in der Matrix stark zu.

Q-Mode | Artvorkommen

Das Problem der doppelten Nullen!

Lösungen

Asymmetrischen Koeffizienten wählen, z.B. Bray-Curtis-(Dis)similaritätsindex → Nachteil: für einige Methoden wie PCA ist Euklidische Distanz Grundlage.
Folgende Standardisierung & anschl. Euklidische Distanz:
- Chord-Standardisierung (+ Euklidische Distanz = Chord Distanz)
  - Variablen werden auf Länge 1 normalisiert.
- Hellinger-Standardisierung (+ Euklidische Distanz = Hellinger Distanz)
  - Abundanzen werden durch die Gesamthäufigkeit des Standorts (Objekts) geteilt und dann die Quadratwurzel gezogen.
- Chord-Standardisierung wurzeltransformierter Abundanzen = Hellinger-Standardisierung → wenn seltene Arten mehr Gewicht bekommen sollen: Hellinger

vegan::decostand()

library(vegan)

### Chord Distanzmatrix
# Chord-Standardisierung
spiderA_chord <- decostand(spiderA, 
  method = "normalize")
# Nun Euklidische Distanz
spiderA_cdist <- dist(spiderA_chord) 

### Hellinger Distanzmatrix
# Hellinger-Standardisierung
spiderA_hell <- decostand(spiderA, 
  method = "hellinger")
# Nun Euklidische Distanz
spiderA_hdist <- dist(spiderA_hell)

Standardisierung bedeutet im Gegensatz zu Transformation, dass die Einträge relativ zu anderen Einträgen transformiert werden.

Clusteranalyse

Was ist Clustering?

Clustering bezieht sich auf ein sehr breites Spektrum von Techniken zum Auffinden von Untergruppen oder Clustern in einem Datensatz.
Wenn wir die Beobachtungen eines Datensatzes clustern, versuchen wir, sie in verschiedene Gruppen aufzuteilen, so dass die Beobachtungen innerhalb jeder Gruppe einander recht ähnlich sind, während sich die Beobachtungen in verschiedenen Gruppen recht stark voneinander unterscheiden.

Typen von Clusteranalyse

Beim hierarchischen Clustering weiß man nicht im Voraus, wie viele Cluster man haben möchte; man erhält eine baumartige visuelle Darstellung der Beobachtungen, ein so genanntes Dendrogramm, das es ermöglicht, die für jede mögliche Anzahl von Clustern (von 1 bis n) erhaltenen Cluster auf einmal zu betrachten.
Beim k-means-Clustering versuchen wir, die Beobachtungen in eine vorgegebene Anzahl von Clustern zu unterteilen.

Hierarchische Clusteranalyse

HC-Algorithmen | Clusterbildung 1

‘Single linkage’ oder ‘nearest neighbor’:

Basierend auf dem kürzesten paarweisen Abstand der Objekte.
Dendrogramm zeigt oft lange Ketten von Objekten und ist nützlich, um einen ersten Überblick zu erhalten

hc_sing <- hclust(spiderA_hdist, method = "single")

‘Complete linkage’ oder ‘furthest neighbor’:

Basiert auf dem weitesten paarweisen Abstand der Objekte
Neigt dazu, viele kleine Gruppen zu bilden, die sich bei größeren Abständen zusammenballen.
Ist kontrastreicher und nützlich, um Diskontinuitäten in den Daten zu erkennen.

hc_comp <- hclust(spiderA_hdist, method = "complete")

HC-Algorithmen | Clusterbildung 2

‘Arithmetic average’:

Basiert auf den paarweisen Durchschnittsabständen aller Objekte.
Gewichtet oder ungewichtet nach der Anzahl der Objekte

hc_ave <- hclust(spiderA_hdist, method = "average") # ungewichtet (UPGMC)
hc_mcq <- hclust(spiderA_hdist, method = "mcquitty") # gewichtet (WPGMC)

‘Centroids’:

Basiert auf dem Abstand zwischen den Schwerpunkten der Cluster.
Gewichtet oder ungewichtet mit der Anzahl der Objekte

hc_cent <- hclust(spiderA_hdist, method = "centroid") # ungewichtet
hc_med <- hclust(spiderA_hdist, method = "median") # gewichtet

‘Ward’s minimum variance’:

Minimierung der Summe der quadrierten Fehler innerhalb der Gruppe = Summe der quadrierten Abstände zwischen den Mitgliedern eines Clusters geteilt durch die Anzahl der Objekte.

hc_ward <- hclust(spiderA_hdist, method = "ward.D2")

HC-Algorithmen | Vergleich

# Standard-Dendrogram erstellen mit plot()
plot(hc_sing, main = "Single", hang = -1)
plot(hc_comp, main = "Complete", hang = -1)
...

HC-Algorithmus: Aber welcher? | 1

Es kommt auf das Ziel der Studie an!
Clustering ist eine explorative Methode, kein statistischer Test!
Die Wahl des Assoziationsmaßes und der Clustering-Methode beeinflusst die Ergebnisse.
Es gibt Kriterien wie
- Kophenetische Korrelation (je höher, desto besser): Korrelation zwischen den Abständen der ursprünglichen Distanzmatrix und den Abständen der Objekte oder Cluster im Dendrogramm (kophenetische Distanzen).
- Gower-Distanz (je geringer, desto besser): die Summe der quadrierten Differenzen zwischen den ursprünglichen Distanzen und den kophenetischen Distanzen.
- → Bei diesen beiden Kriterien schneidet der Average linkage (UPMGA) Algorithmus (method = average) meist am besten ab!

Wie viele Gruppen?

Das hängt ganz vom Ziel der Studie ab! Die Auswahl ist oft subjektiv.
Es gibt viele verfügbare Analysen, die auf verschiedenen Kriterien basieren und bei der Entscheidung helfen können (siehe z.B. Borcard et al. 2011; Kassambara 2017…).

Grafische Darstellung der Fusionsstufen Die ‘Fusionsstufen’ eines Dendrogramms sind die Unähnlichkeits- bzw. Distanzwerte, bei denen eine Fusion zwischen zwei Zweigen eines Dendrogramms stattfindet. Die Diagramme können bei der Entscheidungsfindung helfen; es gibt aber nicht die eine beste Wahl und alles hängt von der Zielsetzung ab.

Code

par(mfrow = c(1,2))
plot(hc_ave, main = "Average: unweighted", hang = -1)

plot(hc_ave$height,
  nrow(spiderA_hell):2,
  type = "S",
  main = "Fusion levels - Average unweighted Algorithmus",
  ylab = "k (number of clusters)",
  xlab = "h (node height)")
text(hc_ave$height,
  nrow(spiderA_hell):2,
  nrow(spiderA_hell):2,
  col = "red")

Finales Dendrogramm

Für Visualisierungen von Clusteranalysen und PCA ist das R Paket factoextra empfehlenswert:

Code

factoextra::fviz_dend(hc_ave, k = 4, # 4 Gruppen
  cex = 0.8, k_colors = c("#2E9FDF", "#00AFBB", "#E7B800", "#FC4E07"),
  color_labels_by_k = TRUE, rect = TRUE, lower_rect = -0.2, 
  main = "Cluster Dendrogram: Average unweighted")

Heatmap mit Dendrogramm

Code

library(pheatmap)
rownames(spiderA_hell) <- spider$samples # damit die Standorte als labels erscheinen

# Wir transponieren hier den Datensatz, damit die Darstellung 
# wie im vorherigen Dendrogramm ist
pheatmap::pheatmap(t(spiderA_hell), cutree_cols = 4, 
  clustering_method = "average", cluster_rows = FALSE)

Eine Heatmap ist eine grafische Darstellung von Daten, bei der Farben verwendet werden, um die Intensität oder Häufigkeit von Werten in einem zweidimensionalen Bereich zu visualisieren.

Principal Component Analysis

Ordinationstechniken

Durch mathematische Verfahren wird eine sog. Dimensionsreduktion durchgeführt, so dass die Lage der Daten in einem zwei- oder dreidimensionalen Koordinatensystem dargestellt werden kann.
Dabei werden Objekte (z. B. Standorte) oder Variablen (z. B. Arten) geometrisch so angeordnet, dass die Abstände zwischen ihnen im Diagramm ihre natürlichen Abstände darstellen.
- Nahe beieinander liegende Standorte im Diagramm werden als ähnlich in z.B. der Artenzusammensetzung interpretiert.
Die Achsen des Diagramms stellen neue Variablen dar, die Zusammenfassungen der ursprünglichen Variablen sind.
Die meisten Methoden beruhen auf der Extraktion der Eigenvektoren einer Assoziationsmatrix.

Beispiele für Ordinationsverfahren

PCA (Principal Component Analysis, Hauptkomponentenanalyse)
CA (Correspondence Analysis, Korrespondenzanalyse)
MDS (Multidimensional scaling, Multidimensionale Skalierung)
CCA (Canonical Correspondence Analysis, Kanonische Korrespondenzanalyse)
DCA (Detrended Correspondence Analysis)
RDA (Redundanz-Diskriminanz-Analyse)

PCA - Hauptkomponentenanalyse

stellt die wichtigste eigenvektorbasierte Methode, arbeitet mit quantitativen Daten und bewahrt den euklidischen Abstand zwischen den Objekten.
findet eine Folge von Linearkombinationen der Variablen, die eine maximale Varianz aufweisen und untereinander unkorreliert sind.
dient nicht nur als Werkzeug zur Datenvisualisierung, sondern erzeugt auch abgeleitete Variablen zur Verwendung in überwachten Lernproblemen.
Abstände zwischen Objekten im sog. Biplot sind eine Annäherung an ihre euklidischen Abstände im multivariaten Raum → Standardisierung bei Abundanzdaten und Daten mit unterschiedlichen Einheiten!
Voraussetzungen:
- lineare Beziehung zwischen den Variablen
- Datensätze sollten multivariat normalverteilt sein
- keine fehlenden Werte

PCA - “Geometrischer” Ansatz | 1

Ursprung des neuen Koordinatensystems wird in die Mitte der Datenpunkte verschoben (Zentrierung).
Rotation des neuen Koordinatensystems, bis die Varianz der 1. Achse maximiert ist (Reduzierung der Restvarianz).

PCA - “Geometrischer” Ansatz | 2

Ursprung des neuen Koordinatensystems wird in die Mitte der Datenpunkte verschoben (Zentrierung).
Rotation des neuen Koordinatensystems, bis die Varianz der 1. Achse maximiert ist (Reduzierung der Restvarianz).

PCA - “Geometrischer” Ansatz | 3

Zusätzliche Achsen müssen unabhängig voneinander sein (=orthogonal).
Visualisierung der reduzierten Dimensionen als sogenanntes “Biplot” (d.h. nur ein Teil der Variation im ursprünglichen Datensatz wird dargestellt).

Scores: Koordinaten von Objekten (hier Standorte) entlang des hypothetischen Gradienten PC1 zu PC2.

Loadings: Koordinaten des Vektorscheitels entlang des hypothetischen Gradienten → Maß für die Korrelation mit den PC-Achsen.

PCA - “Geometrischer” Ansatz | 4

Gesamtvariation: Summe der quadrierten Abstände vom Ursprung
Erklärte Varianz: Summe der quadrierten Projektionen auf die Hauptkomponenten (PC) = λ (Eigenwerte)
Residuale Varianz: Summe der quadrierten orthogonalen Abstände zu den Hauptkomponenten
Nur eine Rotation: Alle Achsen/Hauptkomponenten erklären die Gesamtvarianz!

PCA - Mathematischer Ansatz

Die erste Hauptkomponente Z₁ eines Satzes von Variablen X₁, X₂, X₃, ..,X_p ist die normalisierte lineare Kombination dieser Variablen, welche die größte Varianz hat:

Z_1 = \phi_{11}X_1 + \phi_{21}X_2 + ...+\phi_{p1}X_p

Die Koeffizienten \phi_{11}, .., \phi_{p1} repräsentieren die Ladungen (‘loadings’) der ersten Hauptkomponente; zusammen bilden diese den Hauptkomponenten-Ladevektor, \phi_1 = (\phi_{11}, \phi_{21},.., \phi_{p1})^T.
Die Ladungen werden so eingeschränkt, dass ihre Quadratsumme gleich eins ist, da andernfalls die Festlegung dieser Elemente auf einen beliebig großen Absolutwert zu einer beliebig großen Varianz führen könnte (Normalisierung).

Berechnung der PC ‘Scores’

Angenommen wir haben einen n x p Datensatz (n Zeilen und p Spalten), dann lässt sich jeder Datenpunkt im ursprünglichen Raum durch die lineare Kombination der Hauptkomponenten repräsentiert = PC ‘Score’ z_{ik}:

z_{ik} = \phi_{1k}x_{i1} + \phi_{2k}x_{i2} + ...+\phi_{kk}x_{ip}

mit i=1 bis n als Stichprobenumfang (= Anzahl Objekte) und k=1 bis p Hauptkomponenten

In Matrixform ausgedrückt: \mathbf{Z} = \mathbf{X}*\mathbf{U}

Matrix Z:

Datenpunkte entlang der neuen Hauptkomponenten (PC-Achsen) z_{ik} \rightarrow \mathbf{Z} =\left( \begin{array}{ccc} z_{11} & \cdots & z_{1k} \\ \vdots & \ddots & \vdots \\ z_{i1} & \cdots & z_{ik} \end{array} \right)

(Zentrierte) Datenmatrix X:

Variablen X_k in i Beobachtungen x_{ik} \rightarrow \mathbf{X} =\left( \begin{array}{ccc} x_{11} & \cdots & x_{1k} \\ \vdots & \ddots & \vdots \\ x_{i1} & \cdots & x_{ik} \end{array} \right)

Matrix U der k Eigenvektoren:

Regressionskoeffizienten/Ladungen \phi_{kk} \phi_{kk} \rightarrow \mathbf{U} =\left( \begin{array}{ccc} \phi_{11} & \cdots & \phi_{1k} \\ \vdots & \ddots & \vdots \\ \phi_{k1} & \cdots & \phi_{kk} \end{array} \right)

Manuelle Berechnung (in R)

Für ganz interessierte…

myPCA <- function(X) {
  X_mat <- as.matrix(X)
  object_names <- rownames(X)
  var_names <- colnames(X)
  
  ### 1. Zentrierung der Daten (wird für die Berechnung von Z gebraucht) 
  X_cent <- scale(X_mat, center = TRUE, scale = FALSE)
  
  ### 2. Berechnung der Kovarianzmatrix S
  X_cov <- cov(X_cent)
  
  ### 3. Berechnung der Eigenwerte lambda und der Eigenvektoren v 
  # der Kovarianzmatrix S (s. Legendre & Legendre, 1998, eq. 9.1 und 9.2)
  # Die Eigenwerte und -vektoren erfüllen die Gleichung S*v = lambda*v.
  X_eig <- eigen(X_cov)
  
  # (Eigenwerte sind ein Maß für die Bedeutung (Varianz) der Achsen. Sie 
  # können als "Proportions Explained" (Anteil der erklärten Variation) 
  # ausgedrückt werden, indem sie durch die Summe aller Eigenwerte geteilt 
  # werden.)
  
  ### 4. Eigenvektoren als Matrix U abspeichern
  U <- X_eig$vectors
  rownames(U) <- var_names
  
  ### 5. Matrix Z berechnen
  Z <- X_cent%*%U       # eq. 9.4
  rownames(Z) <- object_names
  
  # Output als Liste mit allen 3 Matrizen
  result <- list(X_eig$values,U,Z)
  names(result) <- c("eigenvalues","U", "Z")
  return(result)
}

myPCA(X = spiderA_hell)

PCA in R

Beispiel mit der PCA() Funktion aus 'FactoMineR'

library(FactoMineR)
pca_facto <- PCA(spiderA_hell, scale.unit = FALSE, graph = FALSE)
  # unsere Daten sind bereits standardisiert, daher 'scale.unit = FALSE'
pca_facto

**Results for the Principal Component Analysis (PCA)**
The analysis was performed on 28 individuals, described by 12 variables
*The results are available in the following objects:

   name               description                          
1  "$eig"             "eigenvalues"                        
2  "$var"             "results for the variables"          
3  "$var$coord"       "coord. for the variables"           
4  "$var$cor"         "correlations variables - dimensions"
5  "$var$cos2"        "cos2 for the variables"             
6  "$var$contrib"     "contributions of the variables"     
7  "$ind"             "results for the individuals"        
8  "$ind$coord"       "coord. for the individuals"         
9  "$ind$cos2"        "cos2 for the individuals"           
10 "$ind$contrib"     "contributions of the individuals"   
11 "$call"            "summary statistics"                 
12 "$call$centre"     "mean of the variables"              
13 "$call$ecart.type" "standard error of the variables"    
14 "$call$row.w"      "weights for the individuals"        
15 "$call$col.w"      "weights for the variables"

Output extrahieren

# Eigenwerte
pca_facto$eig

# Ergebnisse der Variablen
pca_facto$var$coord          # Koordinaten
pca_facto$var$contrib        # Beiträge zu den PCs in %
pca_facto$var$cor            # Korrelation der Variablen mit den PCs
pca_facto$var$cos2           # Qualität der Repräsentation

# Ergebnisse der Objekte (hier Standorte)
pca_facto$ind$coord          # Koordinaten
pca_facto$ind$contrib        # Beiträge zu den PCs in %
pca_facto$ind$cos2           # Qualität der Repräsentation

Anteil der erklärten Varianz

Um die Stärke der einzelnen Hauptkomponenten (PCs) zu verstehen, interessiert uns der Anteil der Varianz, der durch die einzelnen PCs erklärt wird (die Summe ist immer 1 bzw. 100%):

pca_facto$eig

          eigenvalue percentage of variance cumulative percentage of variance
comp 1  0.2391942862             50.2281942                          50.22819
comp 2  0.1149343105             24.1349530                          74.36315
comp 3  0.0619177247             13.0020476                          87.36519
comp 4  0.0153305527              3.2192490                          90.58444
comp 5  0.0139610114              2.9316603                          93.51610
comp 6  0.0086239473              1.8109350                          95.32704
comp 7  0.0075595385              1.5874207                          96.91446
comp 8  0.0047529702              0.9980720                          97.91253
comp 9  0.0038069611              0.7994204                          98.71195
comp 10 0.0031663955              0.6649086                          99.37686
comp 11 0.0019933060              0.4185725                          99.79543
comp 12 0.0009741778              0.2045667                         100.00000

Es gibt so viele Hauptkomponenten, wie es Variablen gibt: in unserem Fall 12.

Wie viele Komponenten (PCs)?

Welche Achsen sind wichtig, d.h. wie viel Varianz erklären sie jeweils?
Gibt keine einfache Antwort und keinen Test.
‘Scree plot’ kann als Anhaltspunkt dienen: Wir suchen nach einem “Ellbogen”.

fviz_eig(pca_facto)

Beiträge der Variablen zu den PCs

p1 <- fviz_contrib(pca_facto, choice = "var", axes = 1, top = 10)
p2 <- fviz_contrib(pca_facto, choice = "var", axes = 2, top = 10)
gridExtra::grid.arrange(p1, p2, ncol = 2)

Ergebnisse visualisieren | Variablen

Darstellung der Ladungen (‘loadings’) der Variablen entlang der PC1/PC2 Achsen (= Maß für die Korrelation mit den PC-Achsen) mit fviz_pca_var():

Code

fviz_pca_var(
  X = pca_facto,  # das PCA Objekt
  repel = TRUE, # Labels sollen nciht ueberlappen
  col.var = "contrib", # Variablenpfeile entsprechend dem Beitrag zur PC1/PC2 einfaerben
  gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07") # Farbwahl
)

Ergebnisse visualisieren | Objekte

Darstellung der einzelnen Standorte anhand ihrer ‘scores’ im neuen 2-dimensionalen Raum mit fviz_pca_ind():

Code

fviz_pca_ind(pca_facto, repel = TRUE)

Ergebnisse visualisieren | Biplot

Gemeinsame Darstellung der ‘scores’ und ‘loadings’ im sog. Biplot mit fviz_pca_biplot():

Code

fviz_pca_biplot(pca_facto, repel = TRUE,
  col.var = "contrib", 
  gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
  col.ind = "#696969" ) # einheitliche Farbwahl Datenpunkte (Objekte)

PCA und (hierarchische) Clusteranalyse

Code

pheatmap::pheatmap(t(spiderA_hell), 
  cutree_cols = 4, 
  clustering_method = "average", 
  cluster_rows = FALSE
)

Code

fviz_pca_biplot(pca_facto, repel = TRUE,
  col.ind = hc_cluster,
  palette = c("#2E9FDF", "#00AFBB", "#E7B800", "#FC4E07"),
  addEllipses = TRUE, 
  legend.title = "Groups"
)

In Cluster 1 gibt es mehrere schwach dominierende Arten, in Cluster 2 kommt besonders häufig Trocterr und Pardlugu vor.Cluster 3 (Standorte 22-28) weist eine ganz andere Gemeinschaftsstruktur auf mit Alopacce und Alopfabr als dominierende Arten. Die Standorte 9-12 (Cluster 3) werden dominiert von der Art Pardmont.
Zwischen Trocterr und Alopacce bzw. Pardmont und Pardlugu gibt es eine besonders starke negative Korrelation.

Zusammenfassung

Welche Informationen haben wir extrahiert?

Wie die Arten miteinander verwandt sind.
Ob Arten an bestimmten Standorten besonders häufig vorkommen.
Ob es Cluster in den Daten gibt, also Gruppen von Daten, die einander ähnlich sind und welche Arten am stärksten zu den Unterschieden beitragen.

Welche Rolle spielen bei der Gemeinschaftsstruktur die Umweltbedingungen? → Übungsaufgabe

Interpretation bei großen Datensätzen?

Beispiel Genexpressionsmessungen → Übung

Code

nci_labs <- NCI60$labs
nci_dat <- NCI60$data
nci_scaled <- scale(nci_dat)
col <- colorRampPalette(c("green", "black", "red"))(255) 

annotation_col = data.frame(nci_labs = nci_labs)
rownames(annotation_col) = rownames(nci_scaled)

pheatmap(t(nci_scaled), cutree_cols = 4, clustering_method = "complete",
  color = col, cluster_rows = FALSE, show_rownames = FALSE,
  annotation_col = annotation_col, fontsize = 7)

Code

pca_nci <- PCA(nci_dat, scale.unit = TRUE, 
  graph = FALSE)
col <- RColorBrewer::brewer.pal(n = 12, 
  name = "Paired")
col[c(13,14)] <- c("grey25", "grey75")
p <- fviz_pca_ind(pca_nci, col.ind = nci_labs, 
  geom.ind = "point",
  legend.title = "nci_labs",  addEllipses=F)
p + scale_color_manual(values = col) +
  scale_shape_manual(values = 11:24)

Lassen sich die Krebszelllinien auf Grundlage ihres Genexpressionsprofils in verschiedene Gruppen oder Cluster einordnen?

Übungsaufgabe

Übung

Analyse der Umweltdaten des spider Datensatzes mittels PCA und hierarchischem Clustering: Gibt es einen Zusammenhang zwischen Umwelt und Geminschaftsstruktur? [Skript “DS3_09A_Uebungen_Clusteranalyse_PCA.Rmd”]
Clusteranalyse des Gensequenzierungsdatensatzes nci [Skript “DS3_09B_Uebungen_Clusteranalyse_PCA.Rmd”]

Die Übungsskripte und Datensätze sind im Moodlekurs (Woche 9) zu finden. Ein kurzes Erklärungsvideo zum R Code ist auch auf Moodle zu finden.

Fragen..??

Total konfus?

Empfehlenswerte Bücher

P. Legendre & L. Legendre (2012): Numerical Ecology, Elsevier Offizielle Webseite
Borcard, Gillet & Legendre (2011): Numerical Ecology with R, Springer https://link.springer.com/book/10.1007/978-1-4419-7976-6
A. Kassambara (2017): Practical Guide To Cluster Analysis in R. Sthda.com (factoextra package)
A. Kassambara (2017): Practical Guide To Principal Component Methods in R. Weblink
Online-Tutorial von A. Kassambara: PCA - Principal Component Analysis Essentials

Cheetsheets

Empfehlenswert ist auch das Cheatsheet des ‘vegan’ Pakets: https://github.com/rstudio/cheatsheets/blob/main/vegan.pdf

Total gelangweilt?

Dann testen Sie doch Ihr Wissen in folgendem Abschlussquiz…

Abschlussquiz

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de

Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.