EDA, Data Mining & Supervised Learning

DS3 - Explorative Datenanalyse & Data Mining

Saskia Otto

Universität Hamburg, IMF

Wintersemester 2023/2024

Lernziele

Am Ende dieser VL- und Übungseinheit werden Sie

• Methoden wie die Explorative Datenanalyse (EDA), das Data Mining, Maschinelles (ML) und Statistisches Lernen (SL) besser einordnen können.
• merken, dass Sie die EDA schon in Ansätzen in den beiden Fallstudien von DS1 und DS3 durchgeführt haben.
• einige grundlegende Methoden des überwachten Lernens (im Engl. ‘Supervised Learning’) verstanden haben und in R anwenden können:
  • 3 verschiedene Methoden der Kreuzvalidierung zur Modelloptimierung und
  • eine der einfachsten Methoden zur Klassifikation: die logistische Regression.

Lernen von Daten

Image by starline on Freepik

Entwicklung der Statistik

• Die Entwicklung der Statistik ist eng gekoppelt an Fragestellungen und Herausforderungen in der Wissenschaft und Industrie.
• In den Anfängen stammten diese Probleme häufig aus landwirtschaftlichen und industriellen Experimenten, waren von relativ geringem Umfang und meist Hypothesen-getrieben → Student’s t-Verteilung und -Test von William Sealey Gosset bei seiner Forschung für die Guinness Brauerei.
• In den 1960ern wurde die “Explorative Datenanalyse (EDA)” maßgeblich von dem Statistiker John W. Tukey entwickelt.
• Mit dem Aufkommen von Computern und dem Informationszeitalter sind die statistischen Probleme sowohl vom Umfang als auch von der Komplexität her explodiert.
• Herausforderungen in den Bereichen Datenspeicherung, -organisation und -suche haben zum neuen Gebiet des “Data Mining” geführt.
• Statistische und rechnerische Probleme in Biologie und Medizin haben die “Bioinformatik” hervorgebracht.
• In vielen Bereichen werden riesige Datenmengen generiert, und die Aufgabe des Statistikers besteht darin, aus all diesen Daten einen Sinn zu machen: wichtige Muster und Trends zu extrahieren und zu verstehen, “was die Daten sagen” → Lernen aus Daten.

EDA vs Data Mining

Die Explorative Datenanalyse (EDA) und Data Mining sind zwei verschiedene, jedoch miteinander verbundene Konzepte im Bereich der Datenanalyse:

Explorative Datenanalyse (EDA)

• Zweck:
  • Daten erkunden, Muster identifizieren, Hypothesen generieren und einen ersten Einblick in die Daten erhalten.
• Methoden und Techniken:
  • Umfasst die deskriptive Statistik, Datenvisualisierung und einfache statistische Tests.
• Stadium im Analyseprozess:
  • Oft der erste Schritt in der Datenanalyse, um die Daten besser zu verstehen und Hypothesen für weitere Analysen zu generieren.
• Zielvariablen:
  • Weniger darauf ausgerichtet, vorherzusagen oder spezifische Zielvariablen zu modellieren.

Data Mining

• Zweck:
  • Verborgene Muster und Zusammenhänge in großen Datenmengen entdecken, um Vorhersagen zu treffen und Muster zu klassifizieren.
• Methoden und Techniken:
  • Fortgeschrittenere statistische und maschinelle Lernmethoden wie Clusteranalyse, Klassifikation, Regression, Assoziationsregeln.
• Stadium im Analyseprozess:
  • Tritt oft in späteren Stadien der Analyse auf, nachdem die EDA durchgeführt wurde.
• Zielvariablen:
  • Fokus auf der Modellierung von Zielvariablen.

EDA Demonstration

• Ansatz zur systematischen Erkundung von Daten, um Muster, Trends und Anomalien zu identifizieren.
• Fokus auf Visualisierung: Tukey betonte die Bedeutung von Grafiken und visuellen Darstellungen bei der Datenexploration. Er erkannte, dass Diagramme und Grafiken oft mehr Einblick in die Daten liefern können als rein numerische Analysen.
• Tukey legte Wert darauf, dass die EDA den oft “unordentlichen” Charakter von realen Daten berücksichtigen sollte. Anstatt sich auf formale Modelle zu verlassen, betonte er flexible und anpassungsfähige Ansätze.
• Integration mit anderen Disziplinen: Die EDA hat sich zu einem interdisziplinären Ansatz entwickelt, der nicht nur in der Statistik, sondern auch in Bereichen wie Maschinelles Lernen, Data Science und Datenanalyse weit verbreitet ist.

Lernen aus den Daten

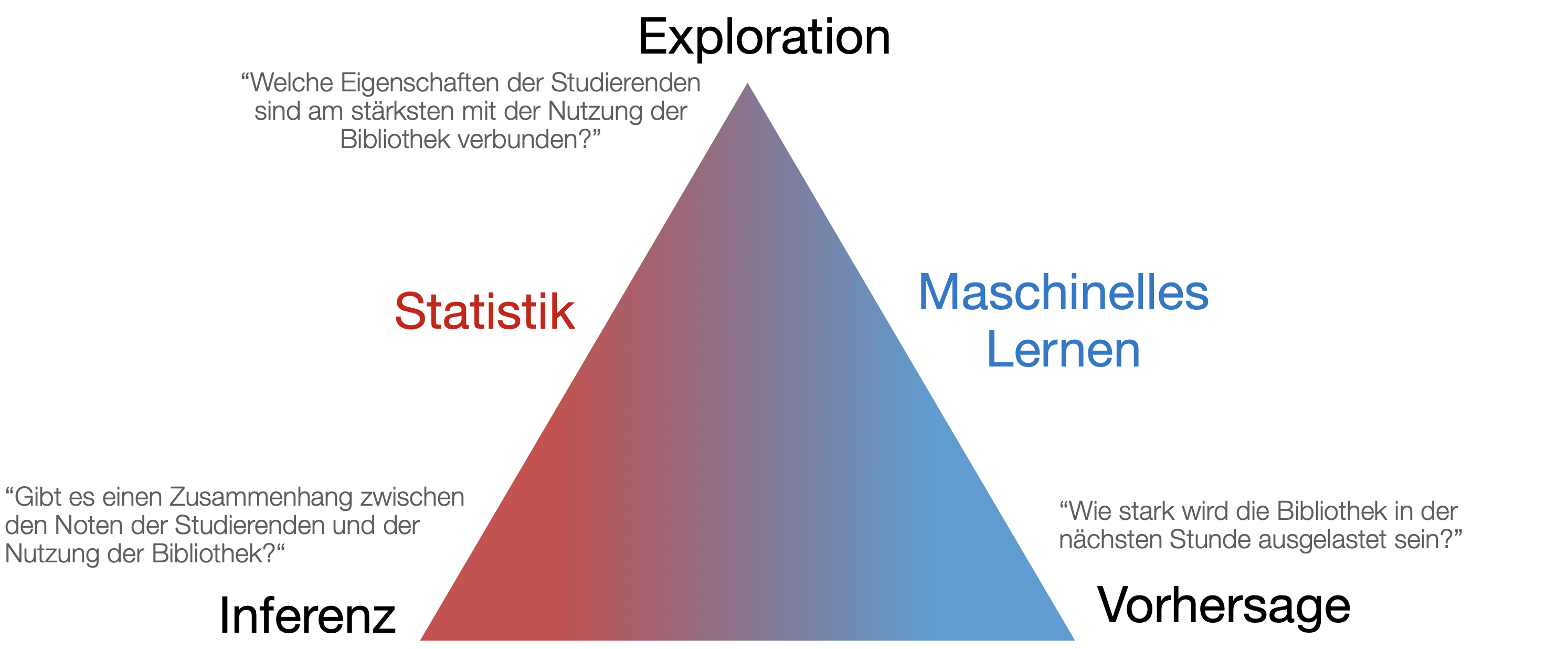
→ Die Wissenschaft des Lernens spielt eine Schlüsselrolle in den Bereichen Statistik, Data Mining und künstliche Intelligenz und überschneidet sich mit Bereichen der Ingenieurwissenschaften und anderen Disziplinen.

Zwei wichtige Ziele bei der Untersuchung biologischer Systeme sind Schlussfolgerungen und Vorhersagen. Bei der Inferenz wird ein mathematisches Modell des Datenerzeugungsprozesses erstellt, um das Verständnis zu formalisieren oder eine Hypothese über das Verhalten des Systems zu testen. Die Vorhersage zielt darauf ab, unbeobachtete Ergebnisse oder zukünftiges Verhalten vorherzusagen, z. B. ob eine Maus mit einem bestimmten Genexpressionsmuster eine Krankheit hat. Die Vorhersage ermöglicht es, die besten Vorgehensweisen zu ermitteln (z. B. die Wahl der Behandlung), ohne dass ein Verständnis der zugrunde liegenden Mechanismen erforderlich ist. In einem typischen Forschungsprojekt können sowohl Schlussfolgerungen als auch Vorhersagen von Nutzen sein - wir wollen wissen, wie biologische Prozesse funktionieren und was als Nächstes passieren wird. Wir möchten zum Beispiel herausfinden, welche biologischen Prozesse mit der Fehlregulierung eines Gens bei einer Krankheit verbunden sind, und feststellen, ob eine Person erkrankt ist, und die beste Therapie vorhersagen.

Viele Methoden der Statistik und des maschinellen Lernens (ML) können im Prinzip sowohl für Vorhersagen als auch für Schlussfolgerungen verwendet werden. Bei den statistischen Methoden liegt der Schwerpunkt jedoch seit langem auf der Inferenz, die durch die Erstellung und Anpassung eines projektspezifischen Wahrscheinlichkeitsmodells erreicht wird. Anhand des Modells lässt sich ein quantitatives Maß für das Vertrauen darauf berechnen, dass eine entdeckte Beziehung einen “wahren” Effekt beschreibt, der mit hoher Wahrscheinlichkeit nicht auf Rauschen zurückzuführen ist. Wenn genügend Daten zur Verfügung stehen, können wir außerdem die Annahmen (z. B. gleiche Varianz) explizit überprüfen und das angegebene Modell bei Bedarf verfeinern.

Im Gegensatz dazu konzentriert sich die ML-Methode auf die Vorhersage, indem sie allgemeine Lernalgorithmen einsetzt, um Muster in den oft umfangreichen und unhandlichen Daten zu finden1,2. ML-Methoden sind besonders hilfreich, wenn man es mit “breiten Daten” zu tun hat, bei denen die Zahl der Eingabevariablen die Zahl der Probanden übersteigt, im Gegensatz zu “langen Daten”, bei denen die Zahl der Probanden größer ist als die der Eingabevariablen. ML macht nur minimale Annahmen über die datenerzeugenden Systeme; sie können selbst dann wirksam sein, wenn die Daten ohne sorgfältig kontrollierten Versuchsplan und in Gegenwart komplizierter nichtlinearer Wechselwirkungen erhoben werden. Trotz überzeugender Vorhersageergebnisse kann das Fehlen eines expliziten Modells jedoch dazu führen, dass ML-Lösungen nur schwer direkt mit dem vorhandenen biologischen Wissen in Verbindung gebracht werden können.

Wie unterscheidet sich ML von statistischer Modellierung?

• ML hat “einfachere” Ziele → sollte genaue Vorhersagen machen.
• Aber wir versuchen nicht, mit ML-Modellen statistische Beweise zu erbringen.
• p-Wert, Verteilung der Residuen, diagnostische Diagramme spiele eine geringe Rolle im ML.
• ML kann für die Untersuchung von Daten und einfache Vorhersagen verwendet werden, sollte aber nicht für “wichtige - Aussagen” verwendet werden.
• Im Allgemeinen auch kein brauchbarer Ersatz für mechanistische Modelle (“irrationales” Verhalten außerhalb des Bereichs der Anpassungsdaten).

Was ist ML?

Was macht ML aus?

ML | Anwendungsbeispiel 1

Bilderkennung

ML | Anwendungsbeispiele 2

• Ermittlung der Risikofaktoren für Prostatakrebs auf der Grundlage klinischer und demografischer Variablen.
• Identifizierung von Mustern in Genexpressionsdaten, um Gene zu identifizieren, die in verschiedenen biologischen Zuständen unterschiedlich reguliert sind → Früherkennung von Krebserkrankungen oder anderen genetisch bedingten Krankheiten.
• Analyse von DNA-Sequenzen, um phylogenetische Beziehungen zwischen verschiedenen Arten zu rekonstruieren.
• Analyse komplexe Metagenomik-Daten zur Erforschung der Rolle von Mikroorganismen in verschiedenen Umgebungen, vom Darm bis zu aquatischen Ökosystemen.
• Analyse von ökologische Daten und Entwicklung von Modellen, die uns helfen, die Verbreitung von Arten vorherzusagen, Ökosysteme zu schützen oder invasive Arten zu kontrollieren.

Was ist statistisches Lernen?

• Maschinelles Lernen ist ein Teilgebiet der Künstlichen Intelligenz.
• Statistisches Lernen entstand als Teilgebiet der Statistik.
• Es gibt viele Überschneidungen - beide Bereiche konzentrieren sich auf überwachte und nicht überwachte Probleme:
  • Beim ML liegt der Schwerpunkt stärker auf groß angelegten Anwendungen und der Vorhersagegenauigkeit.
  • Beim SL liegt der Schwerpunkt auf Modellen und deren Interpretierbarkeit sowie auf Präzision und Unsicherheit.
• Unterscheidung verschwimmt immer mehr.

Beide Methoden (ML und SL) sind datenabhängig. Statistisches Lernen beruht jedoch auf regelbasierter Programmierung; es ist in Form von Beziehungen zwischen Variablen formalisiert, während maschinelles Lernen aus Daten ohne explizit programmierte Anweisungen lernt. Statistisches Lernen basiert auf einem kleineren Datensatz mit wenigen Attributen, im Gegensatz zum maschinellen Lernen, das aus Milliarden von Beobachtungen und Attributen lernen kann. Statistisches Lernen basiert auf Annahmen wie Normalität, keine Multikollinearität, Homoskedastizität usw., während maschinelles Lernen nicht so sehr von Annahmen abhängig ist und diese in den meisten Fällen ignoriert. Beim statistischen Lernen geht es vor allem um Schlussfolgerungen, die meisten Ideen werden aus der Stichprobe, der Grundgesamtheit und der Hypothese abgeleitet, im Gegensatz zum maschinellen Lernen, bei dem Vorhersagen, überwachtes Lernen, unüberwachtes Lernen und halbüberwachtes Lernen im Vordergrund stehen. Statistisches Lernen ist rechenintensiv, basiert auf dem Koeffizientenschätzer und erfordert ein gutes Verständnis Ihrer Daten. Beim maschinellen Lernen hingegen werden durch Iterationen Muster in Ihrem Datensatz identifiziert, was einen weitaus geringeren menschlichen Aufwand erfordert. Auch wenn die meisten argumentieren werden, dass maschinelles Lernen besser ist, stimme ich ihnen bis zu einem gewissen Grad zu. Im Gegenteil, mit der Anwendung des statistischen Lernens machen Sie sich besser mit Ihren Daten vertraut, was Ihnen hilft, das nötige Vertrauen in Ihre Modellierung aufzubauen.

‘Supervised’ vs. ‘Unsupervised’ Learning

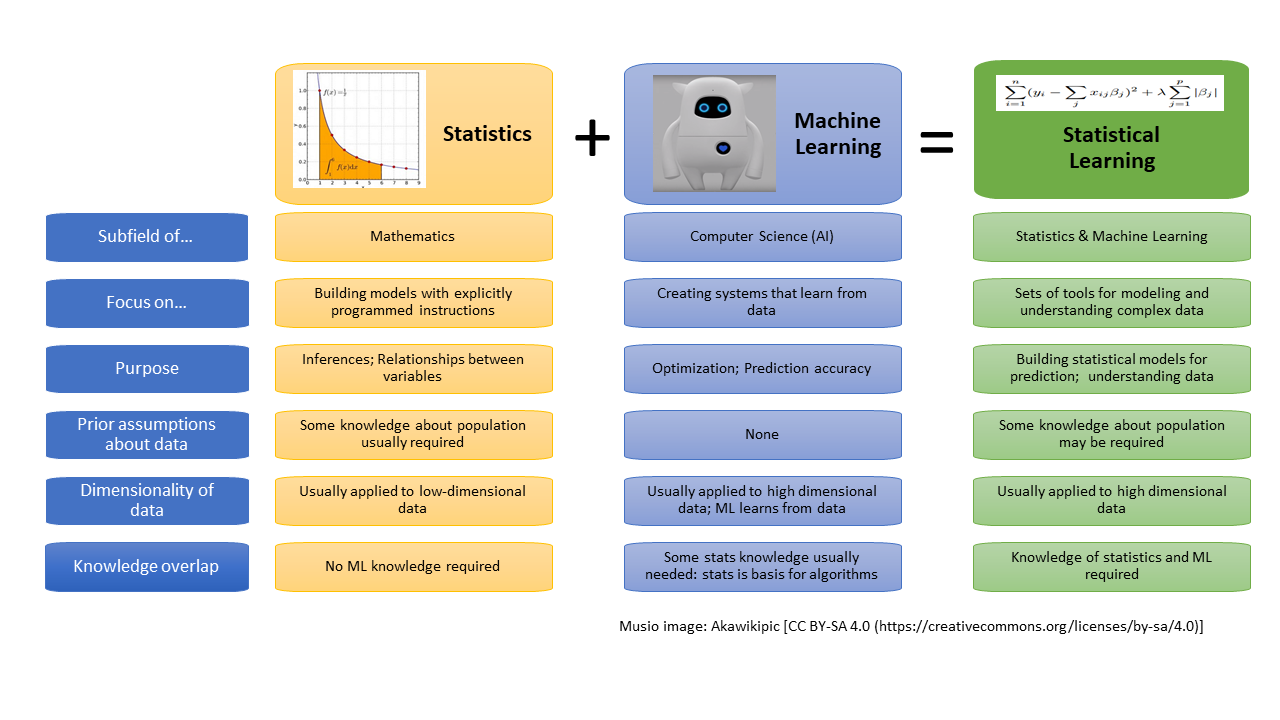
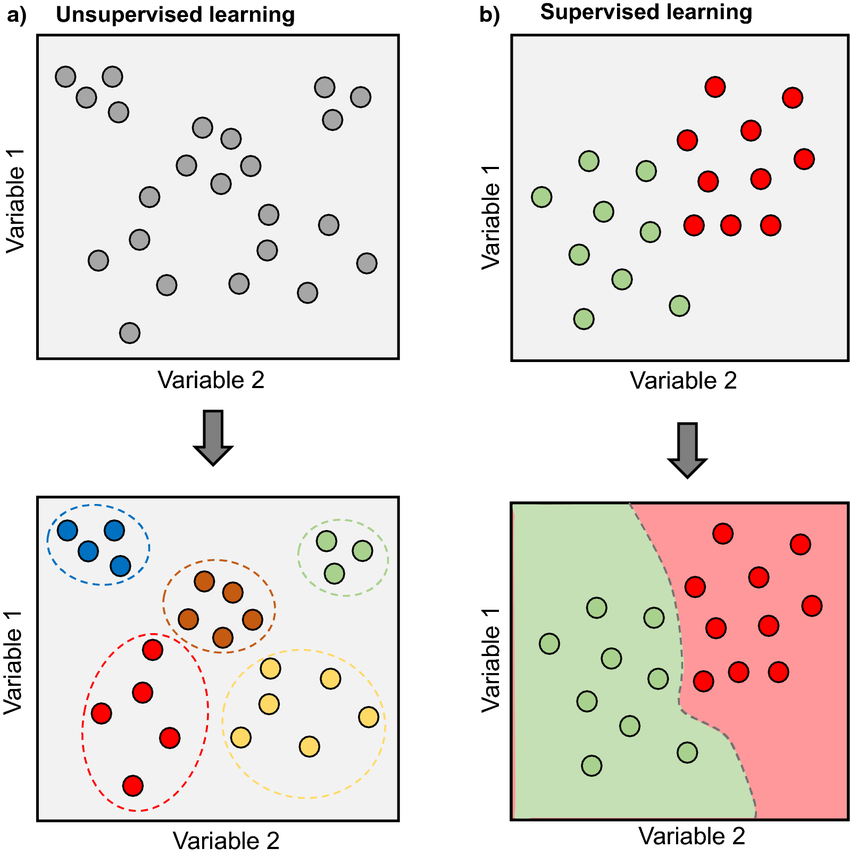
Bildquelle: Morimoto & Ponton (2021): Virtual reality in biology: could we become virtual naturalists?

Im überwachten Lernen (supervised learning) werden Modelle auf Grundlage von Input-Output-Paaren trainiert, während im unüberwachten Lernen (unsupervised learning) Modelle Muster in den Eingabedaten ohne explizite Ausgabeinformationen entdecken.

Supervised Learning | 1

• Ein statistisches Modell wird zur Vorhersage oder Schätzung einer Antwortvariable (Zielvariable, Output) auf der Grundlage einer oder mehrerer unabhängiger Variablen (Inputs) erstellt.
• Dabei ‘lernt’ der Algorithmus aus einem Trainingsdatensatz, indem er iterativ Vorhersagen zu den Daten macht und die vorhergesagte mit der richtigen Antwort vergleicht.
• Ziel ist es, dass der Algorithmus eine Zuordnung von Eingangsvariablen zu Ausgangsvariablen erlernt, die es ihm ermöglicht, Vorhersagen oder Klassifizierungen für neue, nicht gekennzeichnete Daten zu treffen → Optimierung ist das Ziel
• Häufige Verwendung:
  • Klassifizierung verschiedener Dateitypen wie Bilder, Dokumente oder geschriebene Wörter.
  • Vorhersage zukünftiger Trends und Ergebnisse durch Lernen von Mustern in Trainingsdaten mittels Regression .

Supervised Learning | 2

Übersicht beliebter Methoden

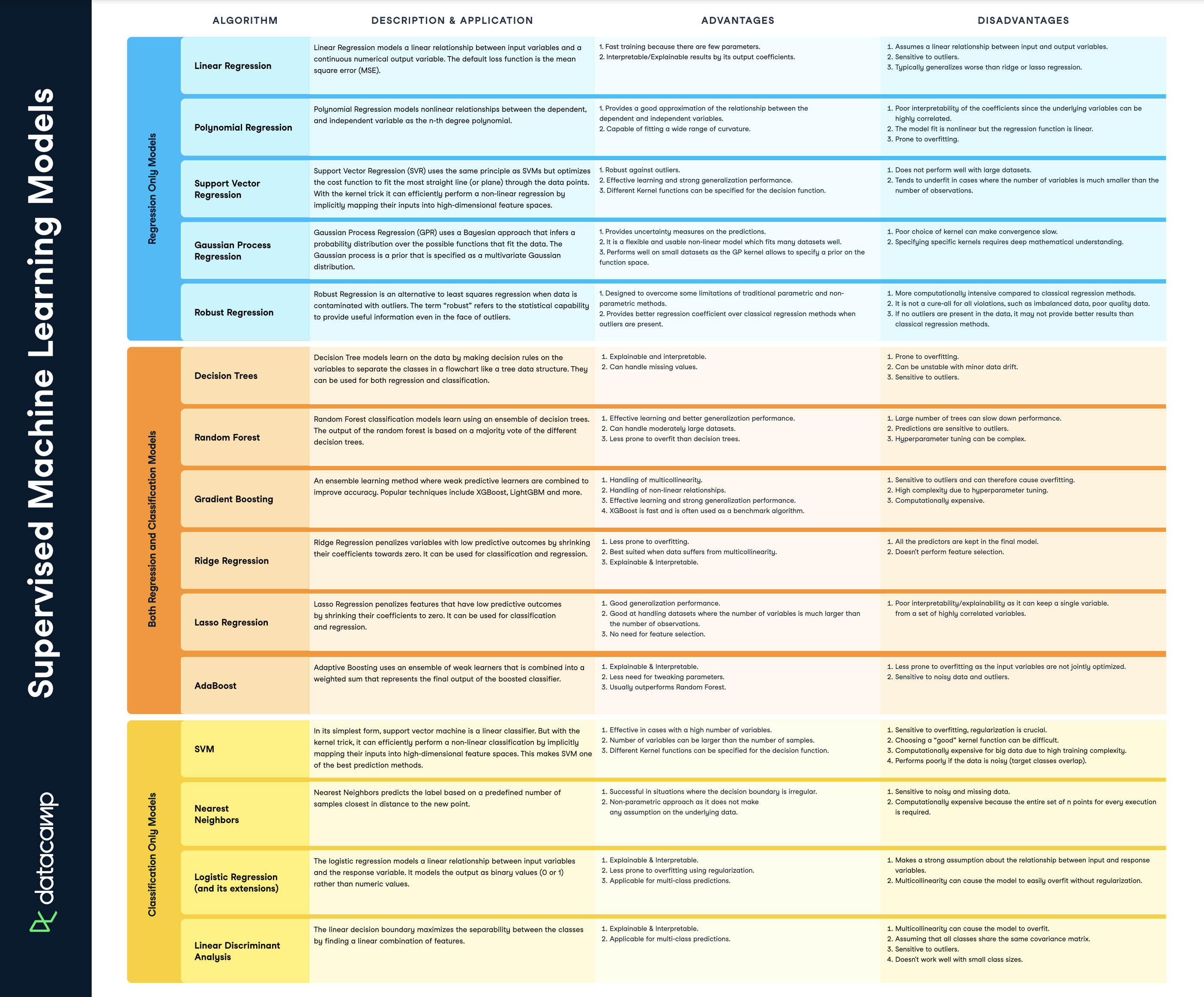
Download-link dieses Cheatsheets: [datacamp.com](https://www.datacamp.com/cheat-sheet/)

Polynomiale Regression: Eine Erweiterung der linearen Regression, bei der nichtlineare Zusammenhänge durch die Einführung von polynomialen Funktionen der unabhängigen Variablen modelliert werden. Dies ermöglicht die Anpassung von Kurven an die Daten.

Ridge Regression (L2 Regularisierung): Eine Regressionsmethode, die eine L2-Regularisierung (ridge penalty) verwendet, um Überanpassung zu verhindern. Sie ist besonders nützlich, wenn es Multikollinearität zwischen den unabhängigen Variablen gibt.

Lasso Regression (L1 Regularisierung): Ähnlich wie Ridge Regression, aber verwendet L1-Regularisierung, um einige Koeffizienten auf genau null zu schrumpfen. Dies ermöglicht automatische Feature-Auswahl.

Elastische Netz Regression: Kombiniert die Ridge- und Lasso-Regression durch Hinzufügen von beiden Regularisierungstermen zur Zielfunktion. Es bietet einen Kompromiss zwischen den beiden Ansätzen.

Support Vector Regression (SVR): Eine Regressionsmethode, die auf den Prinzipien der Support Vector Machines basiert. SVR zielt darauf ab, eine Hyperplane so zu platzieren, dass der größtmögliche Abstand zwischen den Datenpunkten und der Hyperplane erreicht wird.

Entscheidungsbaumregression: Verwendet Entscheidungsbäume, um nichtlineare Zusammenhänge in den Daten zu erfassen. Der Baum wird in einem Top-Down-Ansatz erstellt, indem die Daten in Partitionen aufgeteilt werden.

Random Forest Regression: Eine Ensemble-Methode, die mehrere Entscheidungsbäume kombiniert, um die Vorhersagegenauigkeit zu verbessern und Überanpassung zu reduzieren.

Gradient Boosting Regression: Eine Ensemble-Methode, bei der schwache Modelle schrittweise hinzugefügt werden, wobei jeder neue Baum auf den Fehlern der vorherigen Modelle basiert. XGBoost und LightGBM sind Beispiele für Gradient-Boosting-Methoden.

Was ist Optimimierung? | 1

Suche nach dem Minimum einer Funktion

Was ist Optimimierung? | 2

Suche nach dem Minimum einer Funktion

Einfach für ein oder zwei Parameter…

Was ist Optimimierung? | 3

Suche nach dem Minimum einer Funktion

Nicht einfach für >> 2 Parameter…

Was ist Optimimierung? | 4

• Wir versuchen, die Parameter eines Modells zu bestimmen (z. B. lineare/logistische Regression).
• Wir berechnen die Verlustfunktion für die Parameter unseres Modells zur Bewertung wie gut das Modell die Zielgröße der Trainingsdaten vorhersagt.
• Der Verlust ist die Abweichung zwischen Vorhersage und Beobachtung
• Typische Verlustfunktion, die für die Modellgenauigkeit herangezogen wird: mittlerer quadratischer Vorhersagefehler bzw. ‘Mean Squared Error’. \[MSE = \frac{1}{n}\sum_{i=1}^{n}(Y_i - \hat{Y}_i)^2\]

Ein paar Kompromisse…

• Vorhersagegenauigkeit versus Interpretierbarkeit.
  • Lineare Modelle sind leicht interpretierbar, andere wie ‘thin-plate splines’ sind es nicht.
• Gute Anpassung versus Überanpassung oder Unteranpassung.
  • Wie wissen wir, wann die Anpassung genau richtig ist?
• Sparsamkeit versus Blackbox.
  • Oft bevorzugen wir ein einfacheres Modell mit weniger Variablen gegenüber einem Blackbox-Prädiktor, der alle einschließt.

Flexibilität vs. Interpretierbarkeit

Im Allgemeinen sinkt die Interpretierbarkeit je flexbler eine Methode ist.

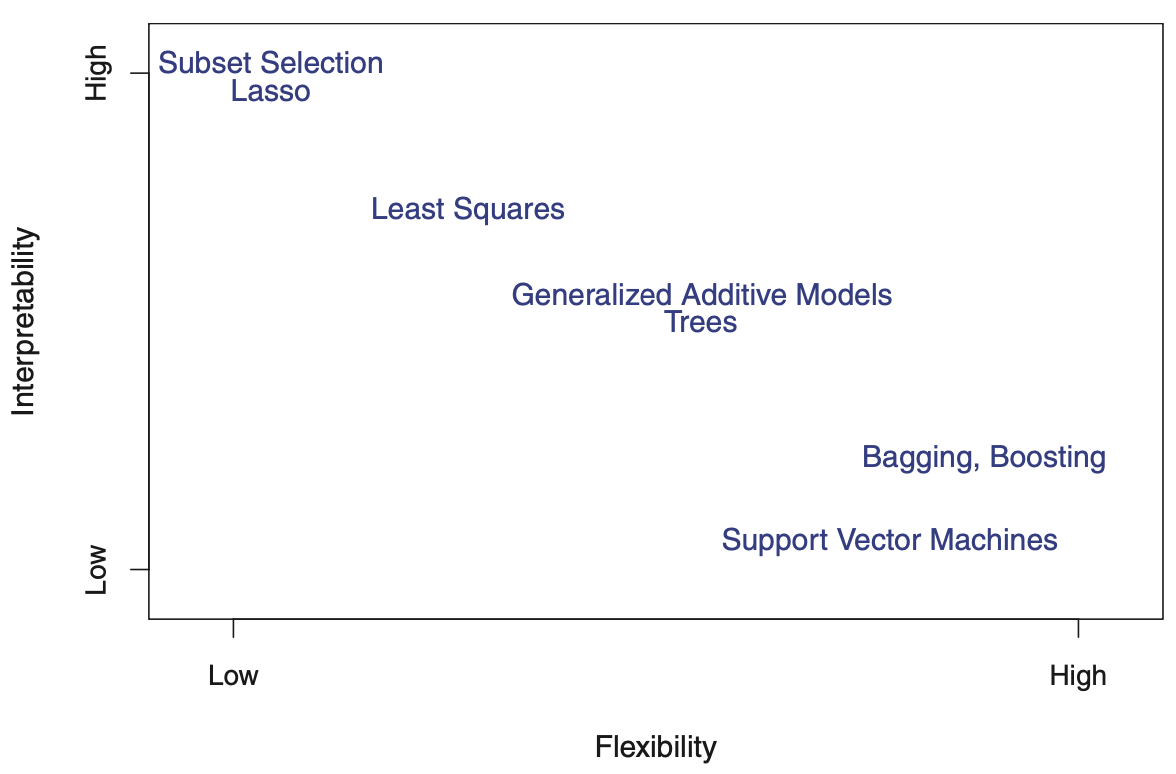
Bildquelle: James et al. (2013): Introduction to Statistical Learning

Performance von Trainings- vs. Testdaten

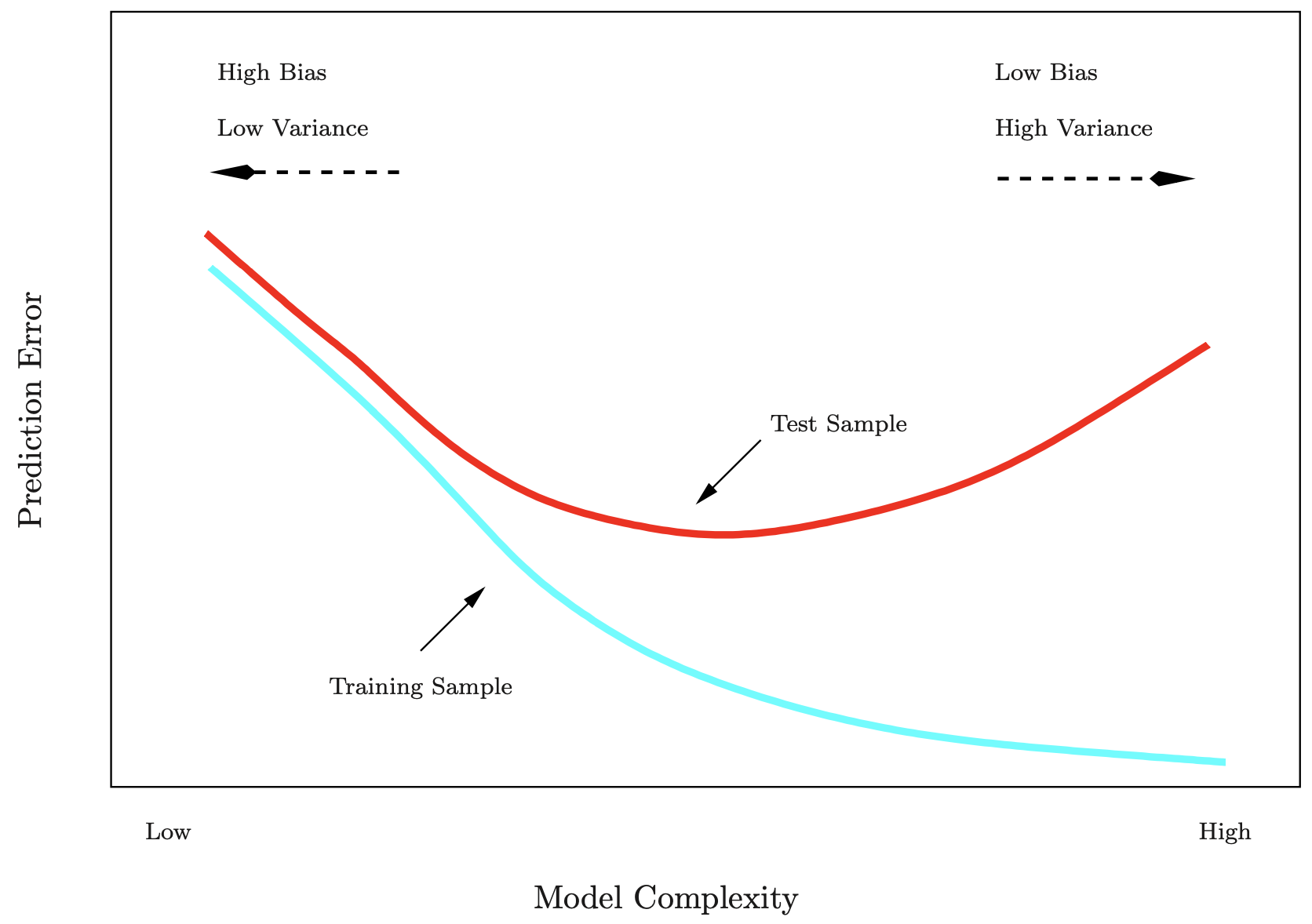
Die Trainingsfehlerrate (\(MSE_{train}\)) unterscheidet sich oft erheblich von der Testfehlerrate (\(MSE_{test}\)). Insbesondere bei sehr flexiblen Modellen kann die Trainingsfehlerrate die Testfehlerrate drastisch unterschätzen.

Bildquelle: James et al. (2013): Introduction to Statistical Learning

Mehr über Vorhersage-Fehlerschätzungen

• Beste Lösung: ein großen festgelegten Testdatensatz → oft nicht verfügbar.
• Faustregel:
  • Training-Test: häufig 80-20%.
  • Bei der Klassifikation: Stellen Sie sicher, dass Sie alle Klassen in den 20 % haben!
  • Wenn nur wenige Daten verfügbar sind: Führen Sie k-fache Kreuzvalidierung durch!
• Beim ML gibt es sogar 3 Typen von Datensätzen: Trainingsdaten (~90%), Validierungsdaten (~10%) und Testdaten (~10%)
• Einige Methoden nehmen eine mathematische Anpassung an der Trainingsfehlerrate vor, um die Testfehlerrate zu schätzen. → AIC, BIC, Cp-Statistik.

Verfahren in ML/SL

• Die Daten erhalten (viele!!!)
• Daten aufbreiten
• Daten in Trainings- und Validierungs-/Testdaten aufteilen
• Einen Modelltyp auswählen
• Entscheiden Sie sich für eine Verlustfunktion
• Optimierungsalgorithmus (und Lernrate) festlegen [ML]
• Anpassen (“Trainieren”) des Modells
• Bewertung der Modellleistung anhand von Validierungs-/Testdaten (und anderen unabhängigen Datensätzen)

Resamplingtechnik: Kreuzvalidierung

3 Typen der Kreuzvalisierung

1. Validation-Set Approach
   • Aufteilung in 50% Trainings- und 50% Testdaten (könnte auch 75/25, 80/20 usw. sein).
   • Besonders üblich in der Zeitreihenanalyse, bei der die Testdaten in der Regel die letzten Jahre sind.
2. Leave-one-out-Kreuzvalidierung (LOOCV)
   • Iterative Methode mit Anzahl der Iterationen = Stichprobengröße.
   • Jede Beobachtung wird einmal zum Testdatensatz.
3. k-fache Kreuzvalidierung

1. Validation-Set Approach

1. Zufällige Aufteilung der verfügbaren Stichprobe in zwei Teile: einen Trainingssatz und einen Validierungs- bzw. Testdatensatz (übliche Aufteilungen sind 50%/50% oder 80%/20% → normalerweise möchte man die Größe des Trainingssatzes maximieren).
2. Anpassung des Modells an den Trainingssatz.
3. Verwendendu der geschätzten Parameter, um die Beobachtungen im Testdatensatz vorherzusagen.
4. Berechnung der Testfehlerrate (z.B. MSE bei Regression, Fehlklassifizierungsrate bei Klassifikation).

Bildquelle: James et al. (2013): Introduction to Statistical Learning

1. Validation-Set Approach | Nachteil 1

• Dieser Ansatz ist konzeptuell einfach und leicht umzusetzen.
• Er hat jedoch zwei potenzielle Nachteile:
  1. Die Validierungsschätzung des Testfehlers kann stark variieren, abhängig davon, welche Beobachtungen im Trainingssatz und welche im Validierungssatz enthalten sind.
  2. Nur ein Teil der Beobachtungen wird zur Modellanpassung verwendet: statistische Methoden neigen dazu, schlechter abzuschneiden, wenn sie auf weniger Beobachtungen trainiert werden.

1. Validation-Set Approach | Nachteil 2

MSE einer einzelnen (schwarz) vs mehrfachen Aufteilung

2. Leave-One-Out CV (LOOCV)

• Iterative Methode mit Anzahl der Iterationen = Stichprobengröße.
• Versucht, die Nachteile des Validierungsset-Ansatzes auszugleichen, indem in jeder Iteration nur eine Beobachtung für die Validierung verwendet wird.

Bildquelle: James et al. (2013): Introduction to Statistical Learning

2. Leave-One-Out CV | Vorgehen

1. Beobachtung #1 aus den Daten entfernen.
2. Das Modell auf die Beobachtungen #2–n anpassen.
3. Die Koeffizienten aus Schritt 2 verwenden, um Beobachtung #1 vorherzusagen und den \(MSE_1\) zu berechnen.
4. Beobachtung #2 aus den Daten entfernen.
5. Anpassung des Modells auf die Beobachtungen #1 und #3–n.
6. Verwendung der Koeffizienten aus Schritt 5, um Beobachtung #2 vorherzusagen und den \(MSE_2\) zu berechnen.
7. Wiederhole dieser Schritte, bis alle Beobachtungen einmal entfernt wurden.
8. Die LOOCV-Schätzung für den \(MSE_{test}\) ist der Durchschnitt dieser n Testfehlerschätzungen: \[CV_{(n)} = \frac{1}{n}\sum_{i=1}^{n}MSE_i\]

2. Leave-One-Out CV | Vor- und Nachteile

• LOOCV ist eine sehr allgemeine Methode und kann bei jeder Art von Vorhersagemodellierung verwendet werden.
• Vorteile
  • Geringere Verzerrung - neigt dazu, die Testfehlerrate nicht so stark zu überschätzen wie der ‘validation-set approach’.
  • Die mehrfache Durchführung von LOOCV liefert immer die gleichen Ergebnisse: es gibt keine Zufälligkeit bei den Aufteilungen in Trainings-/Testdatensätze.
• Nachteile
  • Kann sehr zeitintensiv sein, wenn n groß ist und wenn jedes einzelne Modell langsam anzupassen ist.

3. k-fold CV

• Weit verbreiteter Ansatz zur Schätzung des Testfehlers.
• Schätzungen können verwendet werden, um das beste Modell auszuwählen und eine Vorstellung von der Testfehlerrate des endgültig ausgewählten Modells zu geben.
• Die Idee besteht darin, die Daten zufällig in k gleich große Teile aufzuteilen und iterativ einen Teil als Testdaten zurückzuhalten.

Bildquelle: James et al. (2013): Introduction to Statistical Learning

3. k-fold CV | Vorgehen

1. Zufällige Aufteilung der Beobachtungen in k Gruppen oder ‘folds’ (üblicherweise 5 oder 10) von ungefähr gleicher Größe auf.
2. Der erste ‘fold’ wird als Validierungssatz zurückgehalten und die Methode wird auf den verbleibenden k − 1 ‘folds’ angepasst.
3. Der \(MSE_1\) wird dann für die Beobachtungen im zurückgehaltenen ‘fold’ berechnet.
4. Dieser Vorgang wird k Mal wiederholt; jedes Mal wird eine andere Gruppe von Beobachtungen als Validierungssatz zurückgehalten.
5. Die k-fache CV-Schätzung wird durch Mittelwertbildung der k Schätzungen des Testfehlers, \(MSE_1\), \(MSE_2\), …, \(MSE_k\), berechnet:

\[CV_{(k)} = \frac{1}{k}\sum_{i=1}^{k}MSE_i\]

3. k-fold CV vs. LOOCV

• LOOCV ist ein besonderer Fall des k-fold CV, bei dem k auf n gesetzt wird.
• Vorteil der Verwendung von k = 5 oder k = 10 anstelle von k = n? → der offensichtlichste Vorteil ist der rechnerische.
• Wenn k zu niedrig (< 5) festgelegt wird, wird der Trainingsdatensatz zu klein, und der Vorhersagefehler wird in der Regel nach oben verzerrt.
• Diese Verzerrung wird minimiert, wenn k = n (LOOCV), aber diese Schätzung kann eine hohe Varianz aufweisen.
• k = 5 oder 10 bietet einen guten Kompromiss für dieses ‘Varianz-Verzerrungs-Dilemma’.

Logistische Regression als binäres Klassifikations- verfahren

Klassifikation vs. Regression

• Bei der Klassifikation ist die Zielgröße NICHT kontinuierlich, sondern besteht aus diskreten Kategorien oder Klassen.
• Klassifikation zielt NICHT darauf ab, numerische Werte vorherzusagen, sondern Beobachtungen in vordefinierte Kategorien zu klassifizieren.
• In der Praxis können einige Modelle sowohl für Regression als auch für Klassifikation verwendet werden, und die Unterscheidung hängt von der Art der Zielgröße ab.

Klassifikationsprobleme treten häufig auf, möglicherweise sogar häufiger als Regressionsprobleme.

• Eine Person kommt in die Notaufnahme mit einer Gruppe von Symptomen, die möglicherweise auf eine von drei medizinischen Bedingungen zurückzuführen sein könnten. Welche der drei Bedingungen hat die Person?
• Auf Grundlage von DNA-Sequenzdaten von mehreren Patienten mit und ohne eine bestimmte Krankheit möchte ein Biologe herausfinden, welche DNA-Mutationen schädlich (krankheitsverursachend) sind und welche nicht.

Prinzip der Klassifikation

Beispiel Bilderkennung

Logistische Regression als Klassifikation

• Eigentlich eine Klassifikationsmethode, auch wenn der Name das Wort “Regression” enthält.
• Spezielle Form der Regression, die für binäre Klassifikationsaufgaben entwickelt wurde, bei denen die Zielgröße zwei Klassen hat, zum Beispiel “Ja” oder “Nein”, “0” oder “1”, “positiv” oder “negativ”.
• Wenn mehrere Klassen vorliegen, können Erweiterungen wie die multinomiale logistische Regression verwendet werden.
• Häufig sind wir mehr daran interessiert, die Wahrscheinlichkeit für eine Klasse zu ermitteln:
  • Wie hoch ist die Wahrscheinlichkeit, dass ein Patient mit einer bestimmten Krankheit infiziert ist?
  • → Die logistische Regression macht genau das: anstatt diese nominale Antwortvariable Y direkt zu modellieren, modelliert die logistische Regression die Wahrscheinlichkeit, dass Y zu einer bestimmten Kategorie gehört.
    

Modellierung von Wahrscheinlichkeiten

• Die logistische Regression verwendet eine logistische Funktion (auch als Sigmoid-Funktion bekannt), um die Antwortvariable (Outcome) in einen Wahrscheinlichkeitswert zwischen 0 und 1 zu transformieren.
• Diese Wahrscheinlichkeitswerte werden dann auf einen Schwellenwert angewendet, um die endgültige Klassenzuordnung zu treffen. Wenn die vorhergesagte Wahrscheinlichkeit über dem Schwellenwert liegt, wird die Beobachtung einer Klasse zugeordnet, andernfalls der anderen Klasse.

Bildquelle: http://www.saedsayad.com/logistic_regression.htm

‘Log-Odds’ | 1

Allgemeines Problem

• Y_i (oder die Wahrscheinlichkeiten P_i) sind auf Werte zwischen 0 und 1 beschränkt.
  • sie haben eine obere und untere Grenze
  • sie müssen positiv sein

Lösung

Von Wahrscheinlichkeiten zu den log-transformierten Chancen

• Chancen (odds): \(O_i=\frac{P_i}{(1-P_i)}\) → Verhältnis von Wahrscheinlichkeit des Erfolgs/Misserfolgs
• Vorteil der Chancen: keine obere Grenze, aber dennoch untere Grenze (Chancen können nicht negativ sein)
• Aber log-transformierte Chancen können es sein (auch Logits im Deutschen und ‘log-odds’ im Englischen genannt).

Die Quoten vollführen die gleiche Funktion, allerdings auf einer anderen numerischen Skala. Sie werden beispielsweise in Wettbüros verwendet; die Quoten, dass ein Rennpferd gewinnen wird, können 9 zu 1 sein. Dies bedeutet, dass bei der Organisation von 10 Rennen es wahrscheinlich ist, dass das Pferd 9-mal gewinnt und einmal verliert. In Bezug auf Wahrscheinlichkeiten: Die Wahrscheinlichkeit, dass ein bestimmtes Pferd gewinnt, beträgt 0,9. Das entspricht der Aussage, dass die Quoten 9 sind. Das Schöne an Quoten ist, dass sie keine obere Grenze haben. Nehmen Sie eine Reihe von Werten für πi an, zum Beispiel 0,1, 0,2, 0,3, …, und 0,9, und berechnen Sie die Quoten; sie reichen von etwas Nahezu-Null bis zu etwas sehr Großem.

‘Log-Odds’ | 2

Verschiedene Wahrscheinlichkeiten, Chancen und Logits. Die Tabelle zeigt, wie Logits aus Wahrscheinlichkeiten berechnet werden.

Pi	0.001	0.1	0.3	0.4	0.5	0.6	0.7	0.9	0.999
1-Pi	0.999	0.9	0.7	0.6	0.5	0.4	0.3	0.1	0.001
Oi	0.001	0.11	0.43	0.67	1	1.5	2.33	9	999
Ln(Oi)	-6.91	-2.2	-0.85	-0.41	0	0.41	0.85	2.20	6.91

In der logistischen Regression werden die Log Odds als lineare Funktion der erklärenden Variablen modelliert:

\[ln(O_i) = ln(\frac{P_i}{1-P_i}) = g(x_i) \text{ wobei }g(x_i) = \alpha + \beta_1 X_1 + \beta_2 X_2 + ...\beta_p X_p\]

\[O_i = \frac{P_i}{1-P_i} = e^{g(x_i)} \Rightarrow P_i = \frac{e^{g(x_i)}}{1+e^{g(x_i)}}\]

P_i ist immer zwischen 0 und 1

Beispiel ‘palmerspenguin’

Können wir anhand der Flossenlänge die Artzugehörigkeit (‘Adélie’ oder ‘Gentoo’) bestimmen?

data(penguins, package = "palmerpenguins")
penguins_sub <- penguins |>
  filter(species %in% c("Adelie","Gentoo")) |>
  drop_na() |> 
  mutate(species = fct_drop(species))
pairs(penguins_sub)

Das Modell in R

Der Zusammenhang zwischen Binärdaten und der Bernoulli-Verteilung besteht darin, dass binäre Daten oft durch eine Bernoulli-verteilte Zufallsvariable modelliert werden können. Wenn jedes Element in einer Datenmenge nur zwei mögliche Ausprägungen hat (z.B., ja/nein, Erfolg/Misserfolg, 1/0), dann können diese Daten als Realisierungen von unabhängigen und identisch verteilten (i.i.d.) Bernoulli-verteilten Zufallsvariablen betrachtet werden.

In der Statistik wird die Bernoulli-Verteilung oft als Grundlage für die Modellierung von binären Daten verwendet. Wenn mehrere unabhängige Bernoulli-verteilte Zufallsvariablen kombiniert werden (zum Beispiel durch die Addition der Erfolge), ergibt sich die Binomialverteilung, die für die Modellierung von Summen von unabhängigen Bernoulli-verteilten Zufallsvariablen verwendet wird.

Der ‘summary’ Output

summary(log_reg)

Call:
glm(formula = species ~ flipper_length_mm, family = "binomial", 
    data = penguins_sub)

Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-2.60000  -0.00584  -0.00023   0.01513   1.91868  

Coefficients:
                   Estimate Std. Error z value Pr(>|z|)    
(Intercept)       -147.0506    37.3471  -3.937 8.24e-05 ***
flipper_length_mm    0.7162     0.1805   3.967 7.27e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 364.612  on 264  degrees of freedom
Residual deviance:  20.887  on 263  degrees of freedom
AIC: 24.887

Number of Fisher Scoring iterations: 10

Hier interessieren uns jetzt primär nur die Koeffizienten.

Welche Art wird vohergesagt?

Um zu wissen, welche Arten bzw. Faktorstufes R intern als 1 bzw. 0 kodiert, folgenden Code anwenden:

contrasts(penguins_sub$species) 

       Gentoo
Adelie      0
Gentoo      1

→ Gentoo wird mit 1 kodiert, sprich für diese Art wird die Wahrscheinlichkeit berechnet.

Vorhersagen machen

\[E[Y_i]= P_i = \mu_i = \frac{e^{g(x_i)}}{1+e^{g(x_i)}}= \frac{e^{-147.1}*e^{0.716*\text{flipper_length_mm}}}{1+e^{-147.1}*e^{0.716*\text{flipper_length_mm}}}\]

Wenn die Flossenlänge 195, 200, 205, 210, 215 ist:

fl <- c(195, 200, 205, 210, 215)
pred_fl <- exp(-147.1+0.716*fl) / (1 + (exp(-147.1+0.716*fl)))
pred_fl

[1] 0.0005639392 0.0198403057 0.4206757479 0.9630307907 0.9989310405

→ Die Wahrscheinlichkeit, dass der Pinguin der Art Gentoo zugehört, steigt von < 0.1% auf > 99% mit zunehmender Flossenlänge im Bereich von 195-215mm.

Grafische Modellvalidierung

Code

penguins_sub |>
  mutate(
    species_num = case_when(species == "Gentoo" ~ 1, .default = 0),
    pred = predict(log_reg, type = "response")) |>
  ggplot(aes(x = flipper_length_mm, y = pred)) +
  geom_point(aes(y = species_num)) +
  geom_line() +
  geom_point(data = data.frame(fl = fl, pred_fl = pred_fl),
    mapping = aes(x = fl, y = pred_fl), colour = "red", size = 2.5) +
  geom_hline(yintercept = 0.5, linetype = 2) +
  ylim(0,1) +
  ylab("Probability") +
  theme_light()

Konfusionsmatrix

auch Wahrheitsmatrix oder engl. ‘Confusion Matrix’

Wie oft liegt das Modell mit der vorhergesagten Art richtig und wie oft falsch?

Code

pred_probs <- predict(log_reg, type = "response")
pred_class <- rep("Adelie", nrow(penguins_sub))
pred_class[pred_probs > .5] <- "Gentoo" # 0.5 ist unser Schwellenwert
conf_matrix <- table(pred_class, penguins_sub$species) 

	Adelie_obs	Gentoo_obs
Adelie_pred	144	1
Gentoo_pred	2	118

• Unser Modell hat 144 der Pinguine korrekt als Adelie eingestuft, und 118 korrekt als Gentoo Art.
• Die Anzahl korrekter Vorhersagen beträgt 144 + 118 = 262 von insgesamt 265 Pinguinen → die Modellgenauigkeit (‘accuracy’) liegt somit bei 262/265*100 = 98.9 %.

Validation-Set Approach

Wie wäre unsere Modellperformance, wenn wir 50% der Daten als Testdaten zurückhalten?

	Adelie_obs	Gentoo_obs
Adelie_pred	69	0
Gentoo_pred	1	62

- Die Modellgenauigkeit (‘accuracy’) ist hier sogar noch höher: (69+62)/132*100 = 99.2 %!

Übungsaufgabe

Übung

• Bearbeitung und Besprechung des Übungsskripts DS3_07_Uebungen_CV_und_logistischeRegression.Rmd (im Moodlekurs unter Woche 8 zu finden).
• Bitte das Skript VOR der Übung einmal durchlesen!

Fragen..??

Total konfus?

Buchkapitel und Bücher zum Nachlesen

• Kap. 2 (Statistical Learning), Kap. 4 (Classification) und Kap. 5 (Resampling) in An Introduction to Statistical Learning with Applications in R (ISLR) von Gareth James, Daniela Witten, Trevor Hastie und Robert Tibshirani (2013). Eine freie Ausgabe des eBooks gibt es hier: http://faculty.marshall.usc.edu/gareth-james/
• Hastie et al. (2009): The Elements of Statistical Learning → mathematisch fortgeschrittener als ISLR. eBook ist auf der Webseite frei erhältlich: https://hastie.su.domains/ElemStatLearn/

Total gelangweilt?

Dann testen Sie doch Ihr Wissen in folgendem Abschlussquiz…

Abschlussquiz

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de


Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.