Resampling Techniken

DS3 - Explorative Datenanalyse & Data Mining

Saskia Otto

Universität Hamburg, IMF

Wintersemester 2023/2024

Lernziele

Am Ende dieser VL- und Übungseinheit werden Sie

• das sog. Bootstrap-Verfahrens auf reale Datensätze anwenden können, um Konfidenzintervalle für Punktschätzungen zu erstellen.
• wissen, wie das Bootstrap-Verfahren funktioniert, insbesondere wie Stichproben MIT Zurücklegen aus einer vorhandenen Stichprobe gezogen werden.
• das Konzepts der Permutation von Beobachtungen kennen und wissen, wie Permutationstests auf verschiedene Arten von Daten anzuwenden sind, um Hypothesen über Populationsparameter zu testen.
• in der Lage sein, die Ergebnisse von Permutationstests zu interpretieren und zu verstehen, wie statistische Signifikanz in diesem Kontext definiert ist.
• Permutationstests mit anderen Hypothesentestverfahren zu vergleichen und die Vor- und Nachteile jeder Methode zu verstehen.

Unser Thema heute

Grafik von Nina Garman (Pixabay)

Schätzverfahren und Hypothesentest

Beide Verfahren der inferenziellen Statistik beruhen auf unterschiedlichen Stichprobenverteilung:

1. Schätzverfahren
   • Verwendet die Stichprobenverteilung einer Schätzung.
   • Sie wird verwendet, um Standardfehler und Konfidenzintervalle zu erhalten.
   • Die meisten Methoden gehen davon aus, dass die Stichprobenverteilung annähernd normal ist.

2. Hypothesentest
   • Verwendet die Null-Stichprobenverteilung (oder Nullverteilung): die Wahrscheinlichkeitsverteilung einer Teststatistik, wenn die Nullhypothese wahr ist.
   • Häufig werden die t-, F-, \chi^2- und Normalverteilungen zur Annäherung an die Nullverteilungen verwendet, aus denen die P-Werte berechnet werden.

Schätzverfahren und Hypothesentest

Frage:

Was ist zu tun, wenn die Annahmen der besten verfügbaren Methode verletzt werden und wir nicht auf parametrische Tests und allgemeine lineare Modelle zurückgreifen können?

Antwort: Computerintensive Methoden

Ein Ansatz, bei dem die Leistungsfähigkeit des Computers genutzt wird, um eine Stichprobenverteilung zu erstellen:

1. Schätzverfahren: Bootstrapping
2. Hypothesentest: Permutationstests

Bootstrapping

Punkt- und Intervallschätzung

Zur Erinnerung

• Auf Basis einer Zufallsprobe wird der Bereich geschätzt, wo der gesuchte Populationsparameter liegen könnte.
• Ausgangspunkt ist immer eine Punktschätzung → dann wird ein (symmetrisches) Intervall bestimmt, das Konfidenzintervall KI
• Konfidenz wird als wiederholte Stichprobe interpretiert.
• Kann für jeden Parameter (z.B. Mittelwert, Varianz, ..) berechnet werden.
• Die Breite des Intervalls hängt ab
  • vom Stichprobenumfang, der Varianz der Stichprobe und
  • der festgelegten Wahrscheinlichkeit (= Konfidenzniveau) → üblich: 90%, 95%, 99%

KI vom Mittelwert wenn n > 30

KI_{95\%} = 1.96\cdot\sqrt{\frac{\sigma^2}{n}}

KI vom Mittelwert wenn n < 30

KI_{95\%} = t_{(\alpha/2,df)}\cdot\sqrt{\frac{s^2}{n}}

Intervallschätzung | 1

Zur Erinnerung ein Beispiel aus DS2

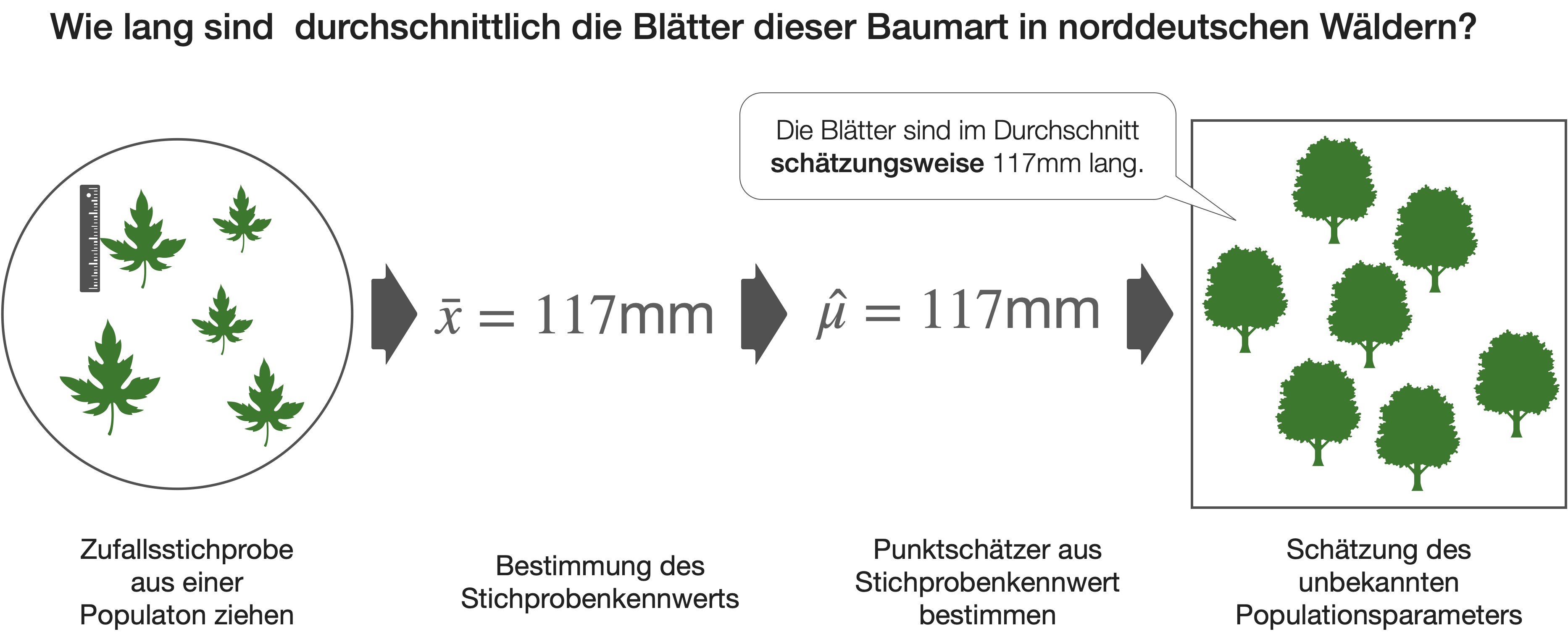
• Wie präzise ist diese Schätzung von 117mm?
• Kann es denn sein, dass der wahre Populationsmittelwert auch 100mm oder 140mm ist und wir einfach Pech mit der Probe hatten?
• In welchem Bereich liegt der wahre Mittelwert höchstwahrscheinlich?

Intervallschätzung | 2

Zur Erinnerung ein Beispiel aus DS2

Die Population

mean(population)

[1] 112.0038

Die Stichprobe

x <- sample(population, 20)
mean(x)

[1] 111.8842

hist(x, main = "Stichprobe (N=20)")

Intervallschätzung | 3

Parametrisches KI basierend auf der t-Verteilung

(x_mean <- mean(x))

[1] 111.8842

(x_se <- sd(x)/sqrt(20) )

[1] 0.2406126

(t_lower <- qt(p = 0.025, df = 19))

[1] -2.093024

(t_upper <- qt(p = 0.975, df = 19))

[1] 2.093024

(CI_lower <- t_lower*x_se)

[1] -0.503608

(CI_upper <- t_upper*x_se)

[1] 0.503608

• → Wir sind uns zu 95% sicher, dass der wahre Mittelwert im Bereich 111.4 - 112.4 liegt (111.9 ± 0.5).
• Unter der Annahme, dass die Verteilung einer symmetrischen t-Verteilung folgt!

Bootstrapping oder ‘Schnürsenkelmethode’

Nicht-parametrische KIs mittels Bootstrapping berechnen

• Nützliche Methode, wenn Verteilung nicht einer theoretischen Verteilung entspricht (z.B. der z- und t-Verteilung).
• Prinzip:
  1. Die Verteilung der Stichprobe dient als Grundlage einer ‘Pseudopopulation’.
  2. Aus dieser ‘Pseudopopulation’ entnehmen wir wiederholt Stichproben und berechnen jeweils die Kenngröße.
  3. Da der Stichprobenumfang meist limitiert ist, werden Proben mit Rücklegen entnommen (somit unendlich groß).
  4. Aus der Grundgesamtheit der Kennwerte (z.B. der Mittelwerte) berechnen wir das untere und obere 2.5 % (oder 0.5 %,..) Quantil als unsere Konfidenzgrenze.
• Ergebnisse sind recht zuverlässig und mit Computern schnell umzusetzen.
• Die KI sind nicht unbedingt symmetrisch.

Bootstrapping | Berechnung

Schritt 1-3: die Schleife

set.seed(123)
it <- 10000 # 10000 Iterationen
boot_mean <- numeric(it) 
for (i in 1:it){
  x_sample <- sample(x, replace = T) # (N auch 20)
  boot_mean[i] <- mean(x_sample)
}

Schritt 4: die Quantilen = KI

# 2.5% und 97.5% Quantilen = 95% Konf.grenzen:
quantile(x = boot_mean, probs = c(0.025, 0.975))

    2.5%    97.5% 
111.4436 112.3769 

# KI:
quantile(boot_mean, c(0.025, 0.975)) - x_mean 

      2.5%      97.5% 
-0.4405603  0.4927287 

→ Wir sind uns nun zu 95% sicher, dass der wahre Mittelwert im Bereich 111.4 - 112.4 liegt.

Bootstrapping | Vergleich

Bootstrapping | ‘boot’ Paket

Statt der manuellen Berechnung können wir die boot() Funktion aus dem gleichnamigen R Paket verwenden:

boot() Funktion im 'boot' Paket

library(boot)

# Definition unserer Funktion zur Mittelwertberechnung
mymean <- function(data, index) {
  sample_mean <- mean(data[index])
  return(sample_mean)
}

# Anwendung der Funktion auf 10000 Stichproben aus x
set.seed(123)
boot_results <- boot(data = x, statistic = mymean, R = 1000)

---

• Die Syntax der Funktion ist recht einfach: boot(data, statistic, R)
  • data repräsentiert den Vektor aus dem die Stichproben gezogen werden.
  • statistic steht für die Funktion, die pro Iteration angewendet werden soll, in unserem Fall für die Berechnung des Mittelwerts.
  • R definiert die Anzahl der Wiederholungsstichproben.

Interpretation | ‘boot’ Paket

Output der boot() Funktion

boot_results

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = x, statistic = mymean, R = 1000)


Bootstrap Statistics :
    original      bias    std. error
t1* 111.8842 0.002644736   0.2475528

Bedeutung der Statistiken

# "original": Mittelwert der 
# Original-Stichprobe
mean(x)

[1] 111.8842

# "bias": Differenz zwischen 
# Mittelwert der Original- 
# und Bootstrap-Stichproben:
mean(boot_results$t) - mean(x)

[1] 0.002644736

# "std. error": St.abw. der
# simulierten Werte
sd(boot_results$t)

[1] 0.2475528

Konfidenzintervalle | ‘boot’ Paket

Built-in Funktion boot.ci() nutzen

boot.ci(boot_results)

BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 1000 bootstrap replicates

CALL : 
boot.ci(boot.out = boot_results)

Intervals : 
Level      Normal              Basic         
95%   (111.4, 112.4 )   (111.4, 112.3 )  

Level     Percentile            BCa          
95%   (111.4, 112.4 )   (111.5, 112.5 )  
Calculations and Intervals on Original Scale

• Normal: parametrisches KI, das auf dem Standardfehler des Mittelwerts und dem Stichprobenumfang basiert
• Percentile: das sog. Bootstrap-Perzentil-Intervall = Quantil aus den Bootstrap-Schätzungen
• BCa: angepasstes Bootstrap-Perzentil-Intervall

Schätzung von KI für Regressionsparameter

Wenn Annahmen nicht erfüllt sind

Code

df$res <- residuals(mod_lm)
df$fit <- fitted(mod_lm)
p1 <- ggplot(df, aes(y)) + 
  geom_histogram(bins = 10, fill = "grey50", colour = "grey10") +
  ggtitle("Histogramm von Y")
p2 <- ggplot(df, aes(x, y)) + geom_point() +
  geom_smooth(method = "lm", se = TRUE) + 
  ggtitle("Beziehung Y ~ X")
p3 <- ggplot(df, aes(res)) + 
  geom_histogram(bins = 10, fill = "grey50", colour = "grey10") +
  ggtitle("Histogramm der Residuen")
p4 <- ggplot(df, aes(fit, res)) + geom_point() + 
  geom_hline(yintercept = 0) +
  ggtitle("Residuen vs. fitted")
gridExtra::grid.arrange(p1, p2, p3, p4)

Die Modellparameter

mod_lm <- lm(y ~ x, df)
summary(mod_lm)$coefficients

              Estimate Std. Error   t value     Pr(>|t|)
(Intercept) -55.960944  22.550127 -2.481624 1.761662e-02
x             8.135234   1.464779  5.553899 2.329342e-06

Parametrische Konfidenzintervalle

(ci_param <- c(
  lower_ci = 8.135234 - 1.96 * 1.464779,
  upper_ci = 8.135234 + 1.96*1.464779))

 lower_ci  upper_ci 
 5.264267 11.006201 

• Der Steigungsparameter b der Stichprobe als Punktschätzer für die Population beträgt 8.1.
• Gegeben, das die Daten normalverteilt und varianzhomogen sind → können wir uns zu 95 % sicher sein, dass bei einer Wiederholung der Datenerhebung die Regressionssteigung für diese neuen Daten zwischen 5.3 und 11.0 liegen würde.

Schätzung von KI für Regressionsparameter

Bootstrapping

set.seed(32)
it <- 10000
boot_b <- numeric(it)
for (i in 1:it){
  n <- nrow(df)
  indices <- sample(1:n, replace = T)
  y_sample <- df$y[indices]
  x_sample <- df$x[indices]
  model <- lm(y_sample ~ x_sample)
  boot_b[i] <- coef(model)[2]
}
quantile(boot_b,c(0.025,0.975))

     2.5%     97.5% 
 4.663306 11.757071 

→ Der Konfidenzbereich liegt nun zwischen 4.7 und 11.8.

Permutationstest

Permutationstests | 1

• Ähnlich wie Bootstrapping, mit dem Unterschied, dass beim Permutationstest Stichproben OHNE Zurücklegen gezogen werden (d.h., wenn ein Wert ausgewählt wurde, kann er nicht erneut ausgewählt werden, so dass kein Wert ein Duplikat sein kann). Dabei werden die Werte einfach neu gemischt.
• Im Falle einer univariaten Statistik (z. B. Mittelwert) ändert sich dadurch nichts.
• Bei zwei oder mehr Variablen bzw. Gruppen ändert sich durch die Umordnung einer Variablen allerdings die Teststatistik, z. B. die Korrelation oder Regression,
  

Permutationstests | 2

Prinzip der Permutation

Man generiert sich mit Hilfe des Computers seine eigene Zufalls- oder Nullverteilung und prüft dann, ob sich die gefundene Verteilung von dieser Zufallsverteilung unterscheidet.

• Annahme: Die gemessenen Werte sind die Werte, die vorkommen können.
• Frage: Mit welcher Häufigkeit tritt die gefundene Verteilung bei den oben generierten Zufallsverteilungen auf?
• Signifikanz: Die Häufigkeit, mit der die gefundene Verteilung bei den durch zufällige Verteilung generierten Gruppen auftritt, entspricht der Irrtumswahrscheinlichkeit.

Demonstration aus dem Internet

Webseite: https://www.jwilber.me/permutationtest/

Was ist besser?

Nicht-parametrische Tests

• Rang-basierte Tests, wie z. B. der Mann-Whitney-U-Test für zwei Stichproben, stellen Permutationstests dar:
  • Daten werden durch Ränge ersetzt und diese permutiert, um eine Nullverteilung zu erzeugen.
  • Die genaue Wahrscheinlichkeitsverteilung der U-Statistik ist bekannt.
  • Durch die Ersetzung der Daten durch ihre Ränge gehen jedoch Informationen verloren.

Permutationstest

• Statt Daten durch die Ränge zu ersetzen können sie direkt permutiert werden.
• Permutationstests haben bei kleinem Stichprobenumfang eine geringere Teststärke als parametrische Tests, aber sie sind aussagekräftiger als z.B. der Mann-Whitney-U-Test.
• Bei großem Stichprobenumfang haben sie eine ähnliche Teststärke wie parametrische Tests.

Annahmen von Permutationstests

• Zufällige Stichproben.
• Bei Gruppenvergleichen der Mittelwert oder Mediane sollte die Verteilung der Variablen in jeder Population die gleiche Form haben.
• Es gilt jedoch: Permutationstests sind robust gegenüber Abweichungen von der Gleichverteilungsannahme, wenn die Stichprobengröße groß ist (stärker als beim Mann-Whitney-U-Test).

Beispiel 1: Zwei-Stichproben-Vergleich

Schneckenrennen

Unterscheiden sich zwei Schneckenarten in ihrer Laufgeschwindigkeit (in m/Stunde)?

Aus: https://www.globaltimes.cn/page/201807/1111861.shtml

Zwei-Stichproben-Vergleich | Daten

A <- c(4,2,7,9,2,8)
B <- c(7,10,9,5,8,11)
Rennen <- data.frame(
  Art = c(rep("A", 6), rep("B", 6)),
  Geschw = c(A,B)
)

Rennen |>
  group_by(Art) |>
  summarise(
    Mittelwert = mean(Geschw), 
    Standardabweichung = sd(Geschw)
  )

# A tibble: 2 × 3
  Art   Mittelwert Standardabweichung
  <chr>      <dbl>              <dbl>
1 A           5.33               3.08
2 B           8.33               2.16

Zwei-Stichproben-Vergleich | t-Test

t.test(Geschw ~ Art, Rennen) # 2-seitige Hypothese

    Welch Two Sample t-test

data:  Geschw by Art
t = -1.9547, df = 8.9658, p-value = 0.08247
alternative hypothesis: true difference in means between group A and group B is not equal to 0
95 percent confidence interval:
 -6.473935  0.473935
sample estimates:
mean in group A mean in group B 
       5.333333        8.333333 

t.test(Geschw ~ Art, Rennen, alternative = "less") # 1-seitige Hypothese

    Welch Two Sample t-test

data:  Geschw by Art
t = -1.9547, df = 8.9658, p-value = 0.04123
alternative hypothesis: true difference in means between group A and group B is less than 0
95 percent confidence interval:
       -Inf -0.1853508
sample estimates:
mean in group A mean in group B 
       5.333333        8.333333 

Zwei-Stichproben-Vergleich | Permutation 1

Permutationstest - einmalig

Differenz beider Mittelwerte als Teststatistik

diff_orig <- mean(Rennen$Geschw[Rennen$Art == "B"])- mean(
  Rennen$Geschw[Rennen$Art == "A"])
diff_orig

[1] 3

Teststatistik bei neuer Stichprobe

set.seed(321)
Rennen_neu <- Rennen
Rennen_neu$Geschw <- sample(Rennen_neu$Geschw, replace = FALSE) # (default)
mean(Rennen_neu$Geschw[Rennen_neu$Art == "B"]) - mean(
  Rennen_neu$Geschw[Rennen_neu$Art == "A"])

[1] -0.3333333

Zwei-Stichproben-Vergleich | Permutation 2

Permutationstest - 10000fach

set.seed(321)
it <- 10000 # 10000 Iterationen
mystats <- numeric(it) 
for (i in 1:it){
  # Schleifenkörper: wir kopieren den Code von eben
}

Zwei-Stichproben-Vergleich | Permutation 2

Permutationstest - 10000fach

set.seed(321)
it <- 10000 # 10000 Iterationen
mystats <- numeric(it) 
for (i in 1:it){
  # Schleifenkörper: wir kopieren den Code von eben
  Rennen_neu <- Rennen
  Rennen_neu$Geschw <- sample(Rennen_neu$Geschw)
  mystats[i] <- mean(Rennen_neu$Geschw[Rennen_neu$Art == "B"]) -   
    mean(Rennen_neu$Geschw[Rennen_neu$Art == "A"])
}

Zwei-Stichproben-Vergleich | Verteilung

Verteilung der 10000 Teststatistiken

hist(mystats)
abline(v = diff_orig, col = "red")

p-Werte für 1-/2-seitige Hypothese

# 1-seitig
(n1 <- sum(mystats >= diff_orig))

[1] 475

(p_val_1sided <- n1/10000)

[1] 0.0475

# 2-seitig (mit absoluten Werten)
(n2 <- sum(abs(mystats) >= 
    abs(diff_orig)))

[1] 940

(p_val_2sided <- n2/10000)

[1] 0.094

Zwei-Stichproben-Vergleich | Interpretation

• Bei 475 von 10000 Permutationen sind die Differenzwerte zwischen den beiden Mittelwerten gleich 3 oder größer (also als die Teststatistik der Originaldaten).
• Damit ist die Wahrscheinlichkeit, dass eine Differenz von ≥ 3 auftritt = 4.8 %.
• Für die 2-seitige Hypothese vergleichen wir die absoluten Werte!
• D.h., die Wahrscheinlichkeit eine solche Teststatistik wie die beobachtete zu erhalten - wenn die 1- bzw. 2-seitige H0 richtig ist - liegt bei 4.8 bzw. 9.4 %. = die Wahrscheinlichkeit, dass die beobachteten Daten unter der Annahme der H0 auftreten, liegt bei <5 bzw. < 10%.

Beispiel 2: Korrelation

set.seed(12)
ds <- data.frame(y = runif(10), x = runif(10))
ds

             y         x
1  0.069360916 0.3926972
2  0.817775199 0.8138806
3  0.942621732 0.3762485
4  0.269381876 0.3808122
5  0.169348123 0.2649184
6  0.033895622 0.4393343
7  0.178785004 0.4576072
8  0.641665366 0.5407075
9  0.022877743 0.6656798
10 0.008324827 0.1126989

Statistik der Originaldaten

# Spearman Korrelationskoeffizient
(cor_orig <- cor(ds$y, ds$x, method = "spearman"))

[1] 0.2242424

Korrelation | Permutation 1

Einmalig

# Resampling nur von Y (zufällige Änderung der Reihenfolge)
ds$resample_y <- sample(ds$y)
ds

             y         x  resample_y
1  0.069360916 0.3926972 0.178785004
2  0.817775199 0.8138806 0.641665366
3  0.942621732 0.3762485 0.269381876
4  0.269381876 0.3808122 0.069360916
5  0.169348123 0.2649184 0.817775199
6  0.033895622 0.4393343 0.942621732
7  0.178785004 0.4576072 0.033895622
8  0.641665366 0.5407075 0.008324827
9  0.022877743 0.6656798 0.169348123
10 0.008324827 0.1126989 0.022877743

# Korrelation mit resample_y 
cor(ds$resample_y, ds$x, method = "spearman")

[1] -0.01818182

Korrelation | Permutation 2

10000-fache Wiederholung

set.seed(123)
it <- 10000
mystats <- numeric(it)
for (i in 1:it) {
    # Schleifenkörper: wir kopieren den Code von eben
}

Korrelation | Permutation 2

10000-fache Wiederholung

set.seed(123)
it <- 10000
mystats <- numeric(it)
for (i in 1:it) {
  # Schleifenkörper: wir kopieren den Code von eben
  mystats[i] <- cor(sample(ds$y), ds$x, 
    method = "spearman")
}

Korrelation | Permutation 3

Verteilung von mystats

data.frame(cor = mystats) |> 
 ggplot(aes(x = cor)) +
 geom_histogram() +
 geom_vline(xintercept = cor_orig, 
   colour = "red")

p-Wert (2-seitige Hypothese)

(n <- sum(abs(mystats) >= abs(cor_orig)))

[1] 5394

(p_val <- n/it)

[1] 0.5394

• INTERPRETATION: die Wahrscheinlichkeit, dass die beobachteten Daten unter der Annahme der H0 auftreten, liegt bei 54 %. Wir können daher die H0 nicht ablehnen, es gibt keine signifikante Korrelation.

Korrelationsbeispiel | ‘coin’ Paket

Es gibt das Paket ‘coin’ , das Permutationstests für verschiedene Tests durchführt. Am besten die Vignette anschauen (vignette("coin", package = "coin"):

library(coin) 
spearman_test(y ~ x, data = ds)

    Asymptotic Spearman Correlation Test

data:  y by x
Z = 0.67273, p-value = 0.5011
alternative hypothesis: true rho is not equal to 0

Vergleich mit Standardfunktion

cor.test(ds$y, ds$x, method = "spearman")

    Spearman's rank correlation rho

data:  ds$y and ds$x
S = 128, p-value = 0.5367
alternative hypothesis: true rho is not equal to 0
sample estimates:
      rho 
0.2242424 

Beispiel 3: ANCOVA

Schnabellänge bei Adélie Pinguinen (Insel Dream)

Das Modell

summary(mod_penguins)

Call:
lm(formula = body_mass_g ~ flipper_length_mm + sex, data = penguin_subs)

Residuals:
    Min      1Q  Median      3Q     Max 
-524.73 -186.57    6.13  128.46  716.22 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)        696.634   1112.928   0.626   0.5341    
flipper_length_mm   14.095      5.918   2.382   0.0209 *  
sexmale            643.629     76.015   8.467 2.34e-11 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 267.3 on 52 degrees of freedom
Multiple R-squared:  0.6585,    Adjusted R-squared:  0.6454 
F-statistic: 50.13 on 2 and 52 DF,  p-value: 7.387e-13

Muster in der Varianz?

plot(mod_penguins, 
  which = 1)

ANCOVA | Permutation 1

Wir extrahieren zuerst die t- und F-Statistiken aus der summary() bzw. drop1() Funktion.

Speichern der Original-Statistiken

mod_sum <- summary(mod_penguins)
mod_drop1 <- drop1(mod_penguins, test = "F")
# str(mod_sum)
# str(mod_drop1)
t_flipper_orig <- mod_sum$coefficients[2, "t value"]
f_sex_orig <- mod_drop1$`F value`[3]

ANCOVA | Permutation 2

Wir schreiben die Schleife

set.seed(123)
it <- 10000 # 10000 Iterationen
mystats_flipper <- numeric(it)
mystats_sex <- numeric(it)
for (i in 1:it){
  # Schleifenkörper
}

ANCOVA | Permutation 2

Wir schreiben die Schleife

set.seed(123)
it <- 10000 # 10000 Iterationen
mystats_flipper <- numeric(it)
mystats_sex <- numeric(it)
for (i in 1:it){
  # Schleifenkörper
  df <- penguin_subs
  df$body_mass_g_shuffled <- sample(df$body_mass_g)
  mod <- lm(body_mass_g_shuffled ~ flipper_length_mm + sex, df)
  mystats_flipper[i] <- summary(mod)$coefficients[2, "t value"]
  mystats_sex[i] <- drop1(mod, test = "F")$`F value`[3]
}

ANCOVA | Permutation 3

Verteilung der Teststatistiken

Code

par(mfrow = c(1,2))
hist(mystats_flipper)
abline(v = t_flipper_orig, col = "red", lwd = 2)
hist(mystats_sex, xlim = c(0,75))
abline(v = f_sex_orig, col = "blue", lwd = 2)

p-Werte (2-seitige Hyp.)

# flipper_length
(n_f <- sum(abs(mystats_flipper)
  >= abs(t_flipper_orig)))

[1] 200

(p_val_f <- n_f / it)

[1] 0.02

# sex
(n_s <- sum(
  abs(mystats_sex) >= abs(f_sex_orig)))

[1] 0

(p_val_s <- n_s / it)

[1] 0

INTERPRETATION: die Wahrscheinlichkeit, dass die beobachteten Daten unter der Annahme der H0 auftreten, liegt bei beiden Kovariaten unter 5 %. Wir können daher heweils die H0 ablehnen, es gibt einen signifikanten Effekt beider Variablen.

Fragen..??

Total konfus?

Buchkapitel zum Nachlesen

• The R Book von M.J. Crawley:
  • Kapitel 8.12 Bootstrap
• Wikipedia zu Bootstrap (https://en.wikipedia.org/wiki/Bootstrapping_(statistics))
• Dokumentation des ‘coin’ Pakets (https://cran.r-project.org/web/packages/coin/vignettes/coin.pdf)

Übungsaufgabe

r

Übung

• Aufgaben im Übungsskript DS3_06_Uebungen_Resampling.Rmd mit abschließendem Quiz in Moodle (zuhause VOR der Übung)
• Gegebenenfalls Anwendung der Resampling-Techniken in Ihrer Fallstudie.
• WÄHREND der Übungsstunde: Besprechung der Lösung und Fragenrunde

R Notebook und Datensätze sind im Moodlekurs (Woche 6) zu finden.

Total gelangweilt?

Dann testen Sie doch Ihr Wissen in folgendem Abschlussquiz…

Abschlussquiz

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de


Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.