Lineare Gemischte Modelle (LME)
DS3 - Vom experimentellen Design zur
explorativen Datenanalyse & Data Mining
Saskia Otto & Monika Eberhard
Universität Hamburg, IMF
Wintersemester 2025/2026
Lernziele
![]()
Am Ende dieser VL- und Übungseinheit werden Sie
- wissen, wie pseudoreplizierte Daten und Daten von verschachtelten bzw. hierarchischen Designs mithilfe linearer gemischter Modelle analysiert werden können.
- die Unterschiede zwischen festen und zufälligen Effekten und deren Bedeutung in einem LME nachvollziehen können.
- Varianzkomponenten in einem LME analysieren und interpretieren können, um die Aufteilung der Gesamtvarianz auf die verschiedenen Ebenen zu verstehen.
- eine bessere Variante zur Analyse der Fallstudiendaten (aus DS2) durchführen können.
Theorie

Was sind Gemischte Lineare Modelle?
- Im Englischen ‘Linear Mixed Effect’ (LME) Modelle genannt.
- Erlauben die Analyse von verschachtelten und hierarchischen Daten.
- Kombination von festen und zufälligen Effekten:
- Feste Effekte: Erlauben Rückschlüsse auf die Behandlungsstufen
- Zufällige Effekte: erfassen die Variabilität innerhalb der verschachtelten Struktur (z.B. Probanden oder Gruppen).
- Je mehr Stufen ein Faktor hat, desto mehr Regressionsparameter müssen berechnet werden, was die Freiheitsgrade reduziert!
- Wenn wir nicht an der genauen Art des Faktoreffekts interessiert sind, können wir ihn als Zufallseffekt einbauen.
Theoretische Grundlage
- Gemischte Modelle erweitern lineare Modelle durch die Einführung zufälliger Effekte
- Grundform des Modells:
y_{ij} = \alpha + \beta x_{ij} + u_j + \epsilon_{ij} u_j \sim N(0, \sigma_u^2) \epsilon \sim N(0, \sigma^2) u_1, u_2,..,u_N, \epsilon_1, \epsilon_2,..,\epsilon_N~~~\text{sind unabhängig}
- y_{ij}: Antwortvariable für Beobachtung i in Gruppe j
- \alpha: Fester Y-Achsenabschnitt, \beta: Fester Effekt der Kovariate x_{ij}
- u_j: Zufälliger Effekt der Gruppe j auf den Y-Achsenabschnitt, \epsilon_{ij}: Fehlerterm oder Residualfehler (Reststreuung)
LME in Matrixnotation
y = \mathbf{X}\beta + \mathbf{Z}u + \epsilon, \quad wobei E \begin{bmatrix} u \\ \epsilon \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \text{ und } var \begin{bmatrix} u \\ \epsilon \end{bmatrix} = \begin{bmatrix} \boldsymbol{G} & 0 \\ 0 & \boldsymbol{R} \end{bmatrix}
- n: Anzahl an Beobachtungen
- p: Anzahl fester Parameter
- q: Anzahl zufälliger Effekte
- \mathbf{X}: n×p Matrix für die festen Effekte \boldsymbol{\beta}
- \mathbf{Z}: n×q Matrix für die zufälligen Effekte \mathbf{u}
- \boldsymbol{\epsilon}: n \times 1 -Vektor mit den Residualfehlern für jede Beobachtung.
- \boldsymbol{G} und \boldsymbol{R} sind die Varianz-Kovarianz-Matrix der zufälligen Effekte und Residuen
Pseudoreplikation
- Fehlerhafte Handhabung von Replikaten.
- Problem:
- Wiederholte Messungen an derselben Einheit werden als unabhängige Datenpunkte betrachtet.
- Es fließen mehr Freiheitsgrade in die Analyse als tatsächlich existieren
- Führt zu verzerrten Ergebnissen und zu niedrigen p-Werten
- Lösung: verschachteltes oder hierarchisches Modell
Verschachteltes Design
- Verschachtelung tritt auf, wenn Einheiten in hierarchischen Ebenen organisiert sind.
- Verschachtelte Modelle erfassen die Variation innerhalb und zwischen den Ebenen.
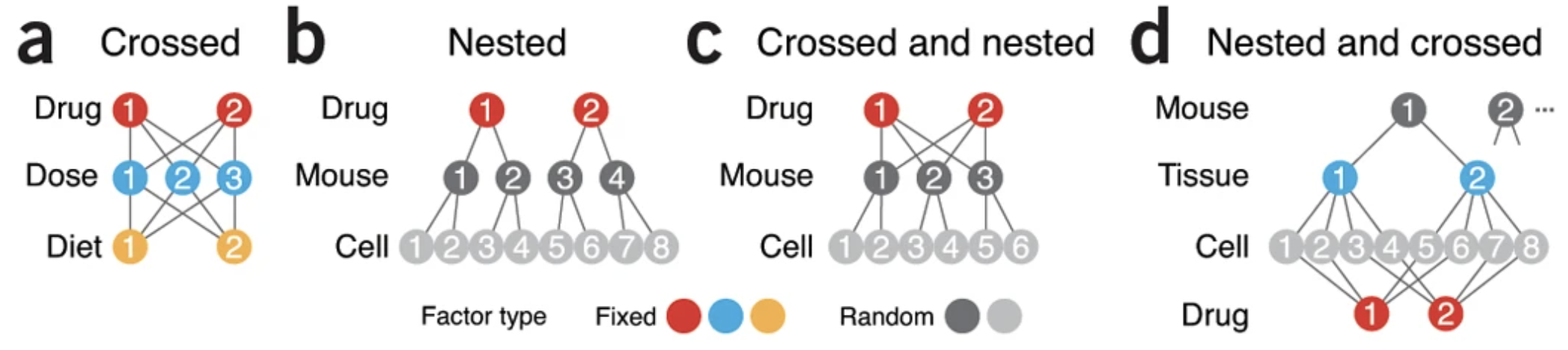
Krzywinski et al. (2014): Nested designs, Nature Methods 11, 977–978
2-faktorielle verschachtelte ANOVA
![]()
- Faktor A mit p Gruppen oder Stufen → fest oder zufällig, aber normalerweise fest
- Faktor B mit q Gruppen oder Ebenen innerhalb jeder Ebene von A → in der Regel zufällig
Beispiel

Mathematische Darstellung:
y_{ijk} = \mu + \alpha_i + u_{j(i)} + \epsilon_{ijk}
- \alpha_i: Fester Effekt der Behandlung (hier Dosis) i
- u_{j(i)}: Zufälliger Effekt der Gruppe (des EK) j, verschachtelt in Behandlung (Dosis) i
- \epsilon_{ijk}: Residualfehler
Komplexe verschachtelte Designs
Beispiel: Räumliche Variabilität von Blattlausdichten
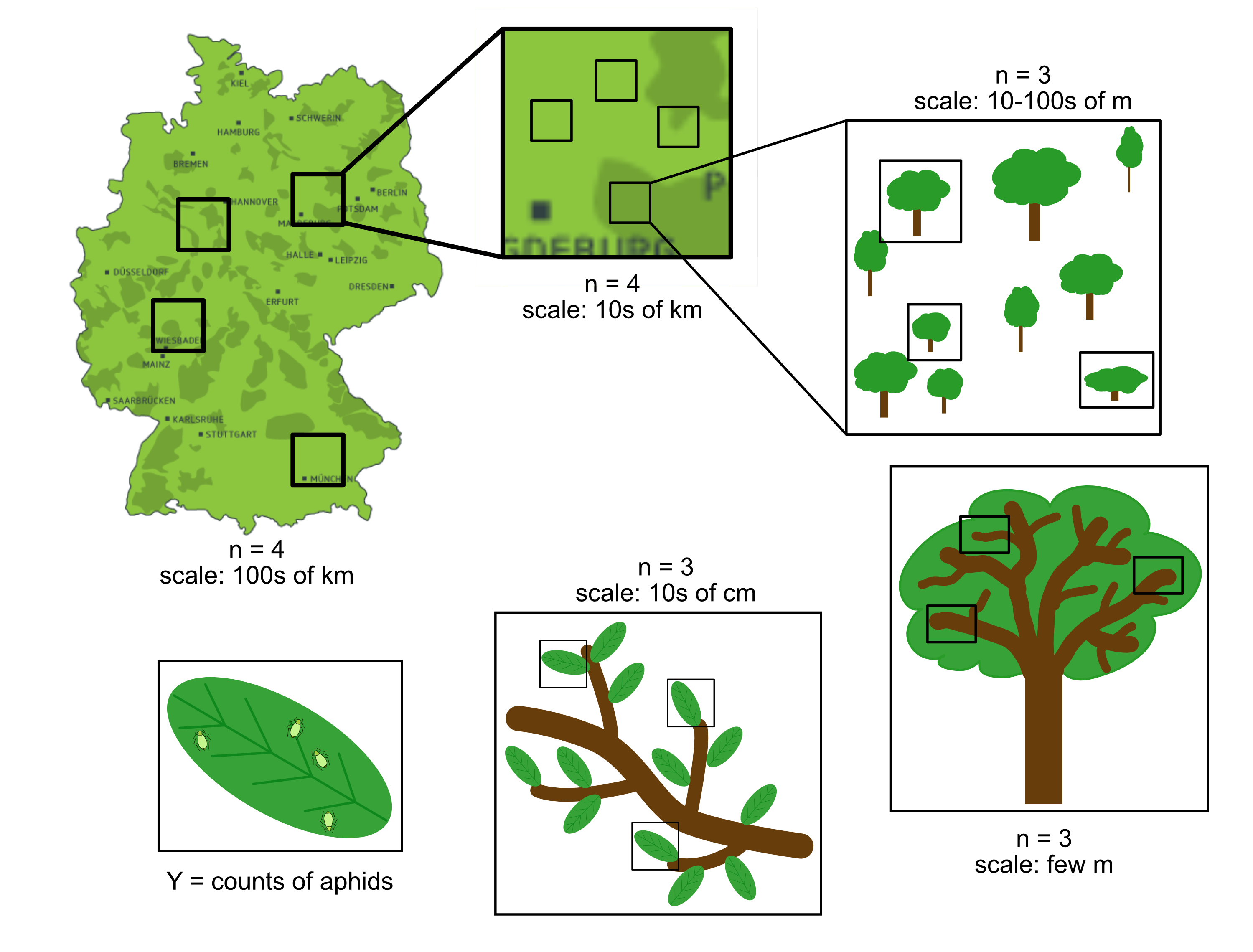
- Gerade bei räumlichen und zeitlichen Feldstudien ist das Beprobungsdesign oft stark verschachtelt.
- → Der größte Beprobungsaufwand sollte auf der Skala mit der höchsten Varianz erfolgen (viele Wiederholungen)!
Best Linear Unbiased Predictor (BLUP) | 1
- Der ‘BLUP’ (beste lineare unverzerrte Schätzung) ist eine Schätzmethode in der Statistik, die in LMEs verwendet wird, um zufällige Effekte vorherzusagen (zufällige Effekte werden vorhergesagt, feste Effekte geschätzt)
- In
aov()ist die Effektgröße \alpha_i einer festen Faktorstufe i definiert als \bar{y}_i - \mu. - In LMEs jedoch verursacht die Korrelation zwischen den Pseudoreplikaten (z. B. Messwiederholungen) innerhalb einer Gruppe eine Verkleinerung der Effekte (sog. ‘Shrinkage’).
- Der BLUP ‘verkleinert’ die Schätzungen im Vergleich zu den festen Effekten:
u_i = (\bar{y}_i - \mu)(\frac{\sigma_u^2}{\sigma_u^2 + \sigma^2/n})
\sigma^2 = Residualvarianz; \sigma^2_u = Varianz zwischen den Gruppen, die die Korrelation zwischen den Pseudoreplikaten innerhalb jeder Gruppe einführt.
Best Linear Unbiased Predictor (BLUP) | 2
- Die BLUPs hängen von der Schätzung der Varianzkomponenten ab, also der Varianz innerhalb und zwischen den Gruppen.
- Je nachdem, wie stark die Variation zwischen den Gruppen ist, können die BLUPs stärker oder schwächer in Richtung des Gesamtdurchschnitts gezogen werden:
- Wenn \sigma^2_u >> \sigma^2/n (d. h., wenn der Großteil der Variation zwischen den Klassen liegt und es wenig Variation innerhalb der Klassen gibt), sind die festen Effekte und die BLUPs ähnlich.
- Wenn \sigma^2_u << \sigma^2/n, können sich die festen Effekte und die BLUPs stark unterscheiden.
Lineare Regression als LME | 1
- Zufällige Effekte können auch in Regressionsmodellen verwendet werden
- Beispiel: Random Intercept Model
Y_{ij} = \beta_0 + \beta_1 X_{ij} + u_j + \epsilon_{ij}
- Y_{ij}: Antwortvariable für Beobachtung i in Gruppe j
- \beta_0: Fester Intercept
- \beta_1: Fester Effekt der Kovariate X_{ij}
- u_j: Zufälliger Intercept für Gruppe j
- \epsilon_{ij}: Residualfehler
Lineare Regression als LME | 2
- Das Random Intercept And Slope Model: hier kann der Achsenabschnitt als auch die Steigung zwischen Gruppen variieren
Y_{ij} = (\beta_0 + u_{0j}) + (\beta_1 + u_{1j})X_i + \epsilon_{ij}
Varianzkomponentenanalyse bei hierarchischen Daten
- Die Varianzkomponentenanalyse dient in LMEs dazu, die Varianz der zufälligen Effekte auf verschiedenen Ebenen eines Modells und der Residuen zu zerlegen.
- Hauptziel: Identifikation der hierarchischen Ebene, auf der der Großteil der Variation entsteht.
- Nutzen: Diese Information ermöglicht es dann, sich in nachfolgenden, detaillierteren Studien gezielt auf Mechanismen zu konzentrieren, die auf dieser Ebene wirken.
Vergleich der Modelle
- Vergleich der Modelle mit AIC, BIC oder Likelihood-Ratio-Tests:
\text{AIC} = -2 \log(L) + 2 k
- L: Likelihood des Modells
- k: Anzahl der Parameter
→ Mehr dazu in der nächsten VL zur multiplen Regression..
Durchführung in R

LME Funktionen

lmer()Funktion aus dem Paket ‘lme4’lme()Funktion aus dem Paket ‘nlme’ → hier vorgestellt:




Überblick Formelschreibweisen

‘Random intercept model’ - nur 1 zufälliger Faktor (B):
Nested 2-way ANOVA - A = fest, B = zufällig (Verschachtelung definiert durch einzigartige IDs):
Nested 4-way ANOVA - A = fest, B und C und D zufällig, D nested in C, nested in B:
Regressionsmodell als ‘random intercept model’ - X = Kovariate:
‘Random intercept and slope model’ - X kommt auch in die ‘random’ Formel:
Weitere anwendbare Funktionen

| Funktion | Ausgabe |
|---|---|
anova(model) |
Data frame mit den Freiheitsgraden, den F- und p-Werten der festen Effekte. |
summary(model) |
Numerische Zusammenfassung des Modells inkl. AIC-, BIC-, und log-Likelihood-Werte. |
plot(model, form) |
Ausgabe eines einzigen Plots, standardmäßig Residuen vs. gefittete Werte; form = optionale Formel, die den gewünschten Diagrammtyp angibt. |
fixed.effects(model) |
Geschätzte Parameter der festen Effekte. |
random.effects(model) |
Vorhergesagte Parameter der zufälligen Effekte. |
VarCorr(model) |
Geschätzten Varianzen, Standardabweichungen (und Korrelationen) zwischen den Termen der Zufallseffekte, Fehler-Varianz und Standardabweichung innerhalb der Gruppen (Residuen). |
R Demo | Design und Datensatz
![]()
Verschachteltes Design
- N: 8 (Exp. Units: Erlenmeyerkolben)
- n: 3 (Objektträger als Unterproben pro EK)
- Effekte: Dosis = {0, 100} (fest), EK = {1,2,3,..,8} (zufällig)
- Freiheitsgrade:
\begin{align*} \text{Zellzahl} &= \text{Dosis} + \text{Fehler}\\ \text{(N - 1)} &= \text{(p - 1)} + \text{(N - p)}\\ \text{(7)} &= \text{(1)} + \text{(6)} \end{align*}

# A tibble: 24 × 5
obj_id dosis_fac ek_id_fac ek_falsch_codiert zellzahl
<int> <fct> <fct> <fct> <dbl>
1 1 0 1 1 63
2 2 0 1 1 56
3 3 0 1 1 48
4 4 0 2 2 55
5 5 0 2 2 56
6 6 0 2 2 64
7 7 0 3 3 55
8 8 0 3 3 55
9 9 0 3 3 54
10 10 0 4 4 39
11 11 0 4 4 51
12 12 0 4 4 44
13 13 100 5 1 79
14 14 100 5 1 93
15 15 100 5 1 87
16 16 100 6 2 92
17 17 100 6 2 96
18 18 100 6 2 92
19 19 100 7 3 86
20 20 100 7 3 87
21 21 100 7 3 82
22 22 100 8 4 88
23 23 100 8 4 85
24 24 100 8 4 78R Demo | LME - richtig kodiert
![]()
R Demo | Falsche Kodierung
![]()
Wenn die ID der Erlenmeyerkolben nicht einmalig ist
numDF denDF F-value p-value
(Intercept) 1 19 858.3768 <.0001
dosis_fac 1 19 267.1188 <.0001Konsequenzen falscher Kodierung
- Hier denkt R, dass das Design für Dosis und Erlenmeyerkolben gekreuzt und nicht genestet ist.
- Entsprechend sind die Freiheitsgrade des Nenners (Denominators) gleich der FG der Residuen (19 statt 6) → somit ist der F-Wert höher → und konsequenterweise der p-Wert niedriger.
- Dies führt dazu, dass wir schneller die H0 (fälschlicherweise) ablehnen (→ stat. Fehler 1. Art).
R Demo | Modellvalidierung

R Demo | Koeffizienten extrahieren

R Demo | Visualisierung

Code
# Vorhersagen für feste und zufällige Effekte berechnen
df$predictions_fixed <- predict(mod_lme, level = 0) # nur feste Effekte
df$predictions_total <- predict(mod_lme, level = 1) # feste und zufällige Effekte
ggplot(df, aes(x = dosis_fac)) +
geom_point(aes(y = zellzahl, color = "Beobachtete Werte"), size = 2) +
geom_point(aes(y = predictions_total, color = "Gesamte Vorhersage (feste + zufällige Effekte) pro EK"), size = 3) +
geom_point(aes(y = predictions_fixed, color = "Nur feste Effekte"), size = 4, shape = 1) +
labs(y = "Zellzahl", x = "Dosis", color = "Legende") +
theme_bw(base_size = 16)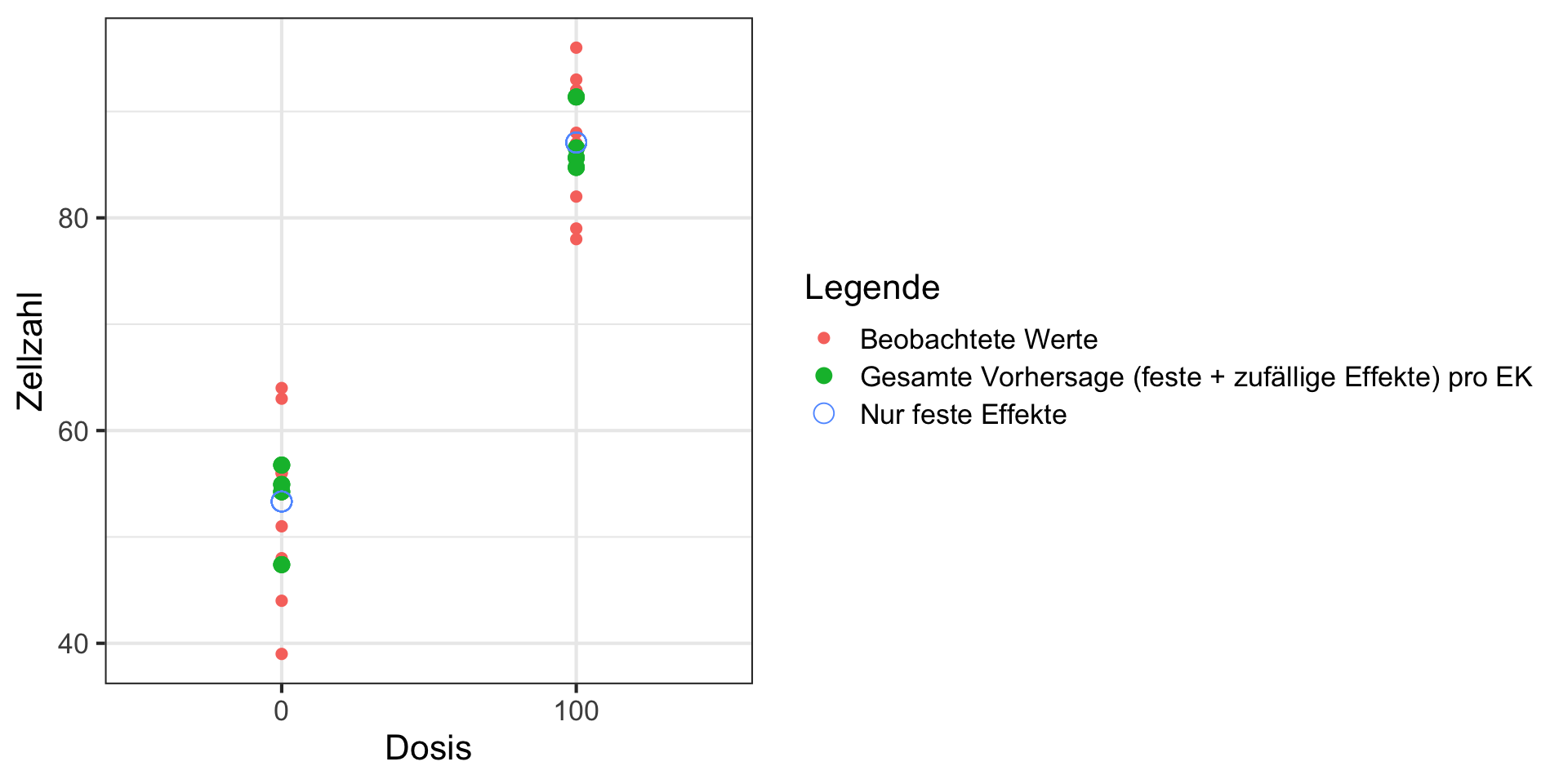
R Demo | Analyse der Varianz-Komponenten

ek_id_fac = pdLogChol(1)
Variance StdDev
(Intercept) 18.60648 4.313523
Residual 25.66667 5.066228- 42% der zufälligen Variation wird durch Unterschiede zwischen den Erlenmeyerkolben erklärt (Intercept-Komponente).
- 58% der zufälligen Variation stellen die Unterschiede zwischen den Objektträgern innerhalb der Erlenmeyerkolben dar (Residual-Komponente = within-group error).
Praxisbeispiel 1:
2-faktorielles Design mit 1 verschachtelten Faktor
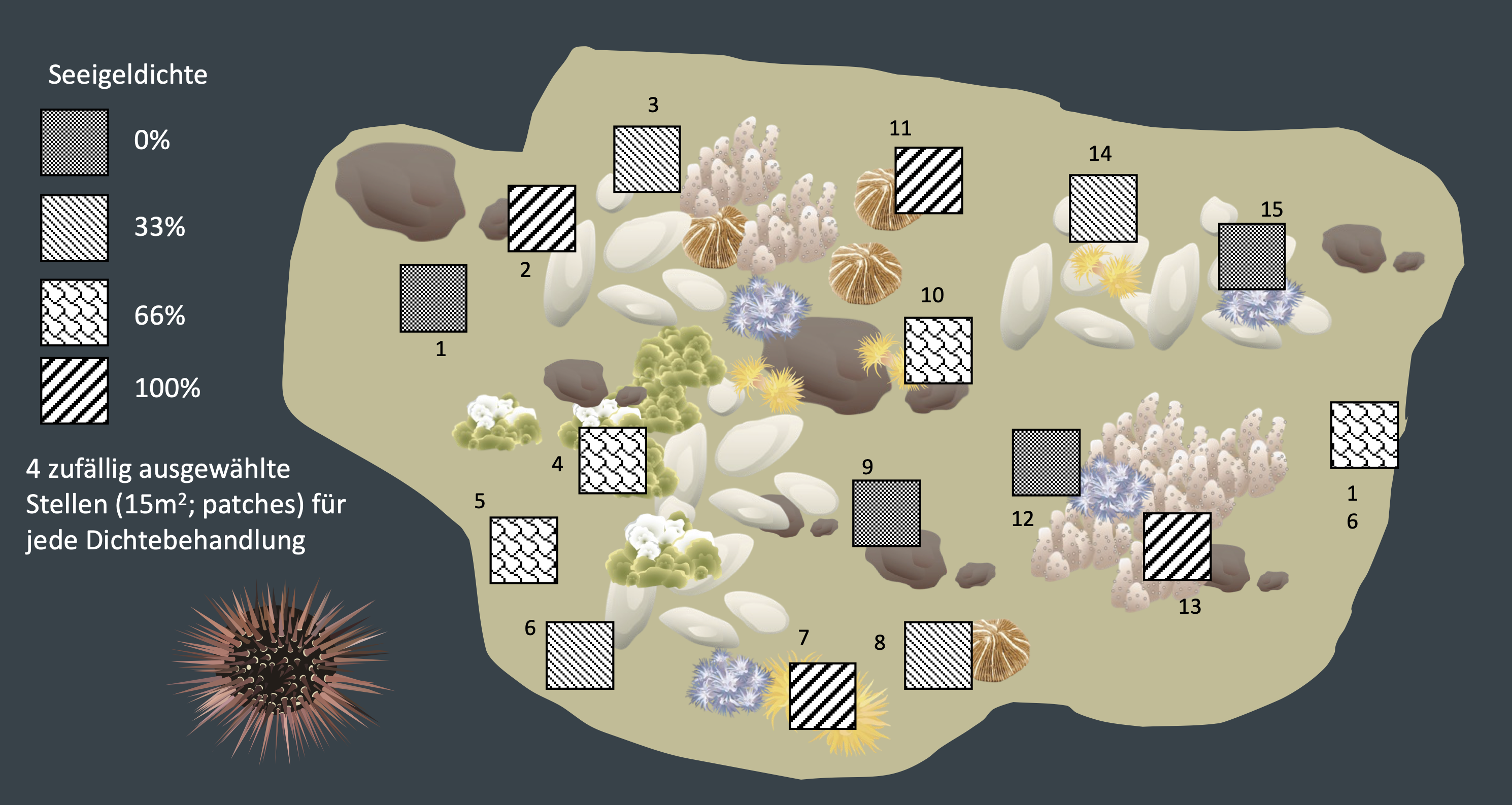
Einfluss der Seeigelbeweidung im Korallenriff
![]()
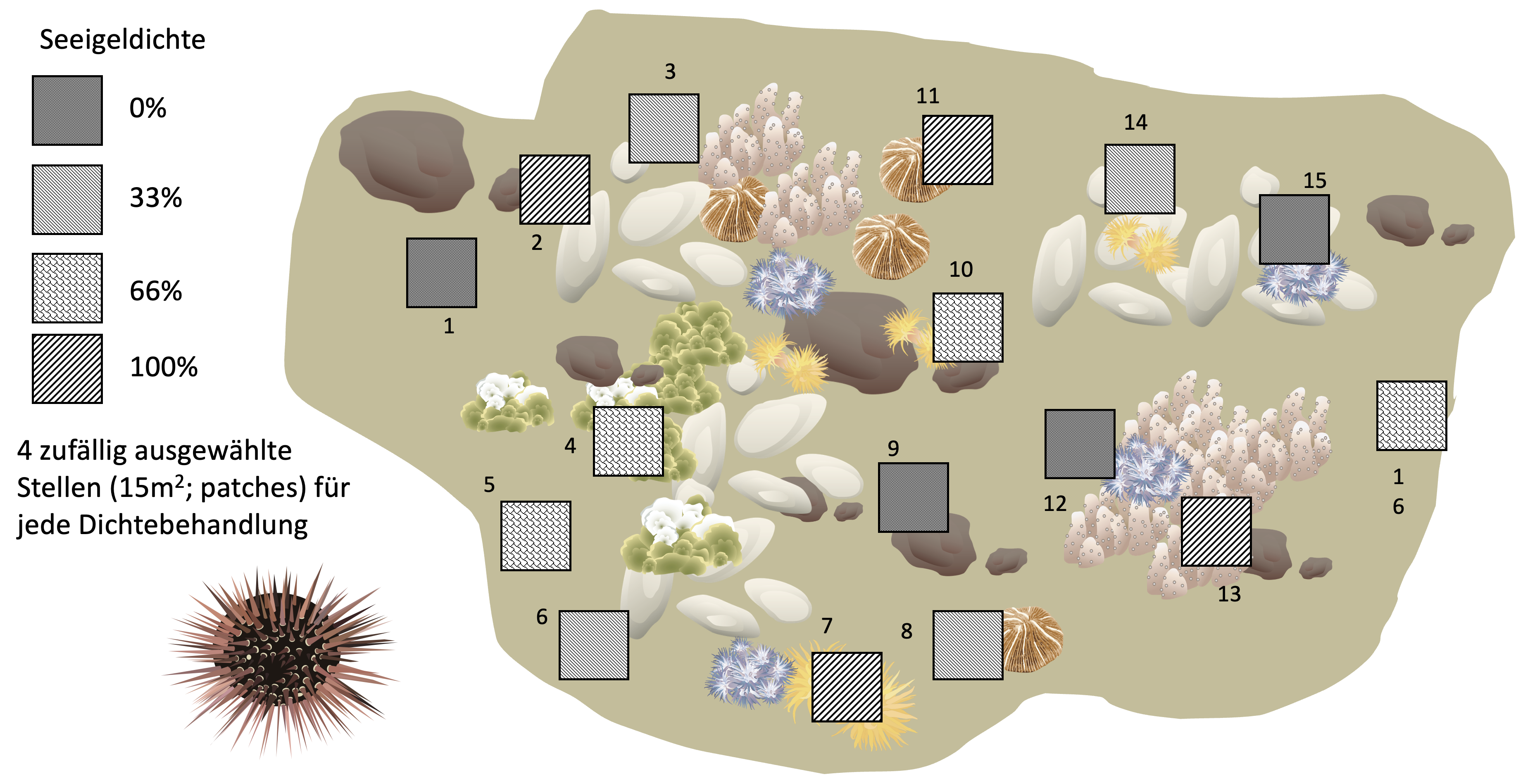
Beispiel ist aus Kapitel 9.1 in Quinn & Keough (2002): Experimental Design and Data Analysis for Biologists
- Andrew & Underwood (1993) manipulierten die Dichte von Seeigeln in der flachen subtidalen Region eines Standorts in der Nähe von Sydney, um die Auswirkungen auf den prozentualen Bewuchs mit Fadenalgen zu testen.
- Es gab vier Seeigelbehandlungen: keine Seeigel, 33% der ursprünglichen Dichte, 66% der ursprünglichen Dichte und 100% der ursprünglichen Dichte.
- Die Behandlungen wurden an vier verschiedenen Stellen (3-4 m^2 Flächen) pro Behandlung wiederholt, und der prozentuale Bewuchs mit Fadenalgen (Antwortvariable) wurde in fünf zufälligen Quadraten pro Stelle gemessen.
- Es handelt sich somit um ein verschachteltes Design mit Behandlung (fester Faktor), Stellen (im Engl. ‘patches’) innerhalb der Behandlung (zufälliger Faktor) und Quadraten als Replikate.
Seeigelbeweidung im Korallenriff
Das Design
![]()
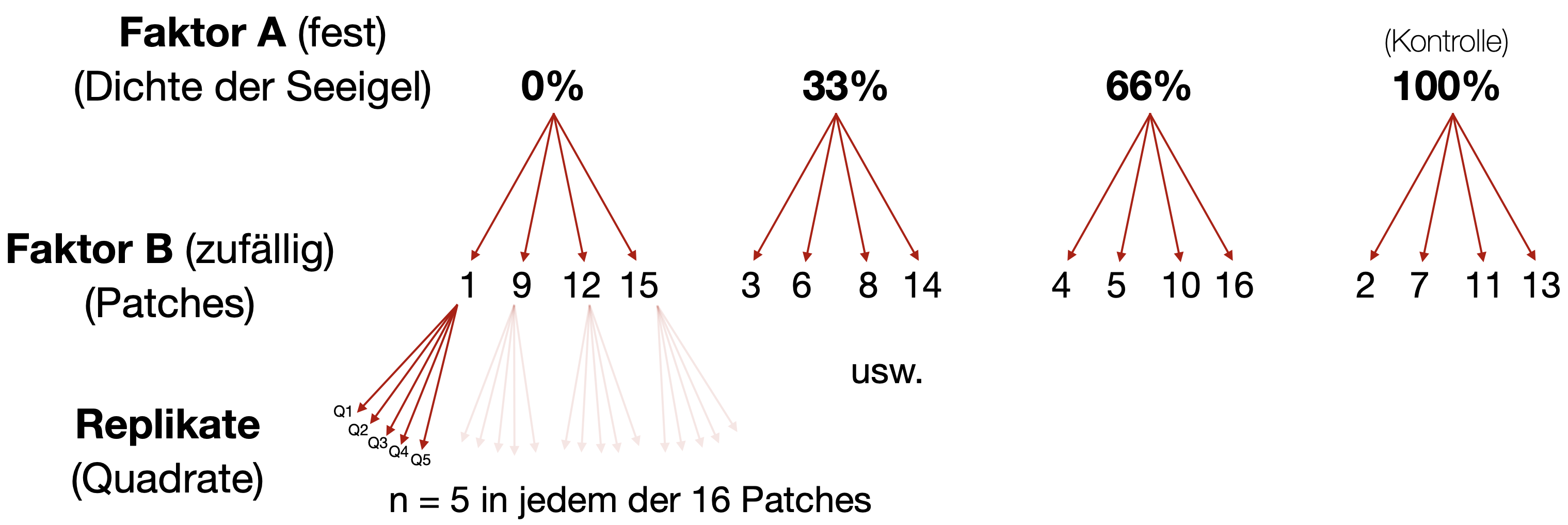
- Jeder Patch (15 m^2) ist zu groß, um ihn zu erfassen ➜ 5 Quadrate (3-4 m^2) als Unterprobe
- Patches werden zu Faktor B innerhalb von Faktor A
- Rest: 5 Wiederholungsquadrate in jedem Patch innerhalb jeder Dichtestufe
Gleichung und Hypothesen
![]()
Gleichung
Y_{ijk} = \mu + \alpha_i + u_{j(i)} + \epsilon_{ijk}
\Rightarrow \text{Fadenalgenbedeckung}_{ijk} = \mu + \text{Seeigeldichte}_i + \text{Patch}_{j(i)} + \epsilon_{ijk}
Wir testen 2 Hypothesen
H0_{Seeigeldichte}: \alpha_1 = \alpha_2 = .. \alpha_i = 0
- → d.h. es gibt keinen Unterschied in der durchschnittlichen Menge an Fadenalgen zwischen den vier Seeigeldichten
H0_{Patches}: \sigma_{u}^2 = 0
- → d.h. es gibt keine signifikante Variabilität zwischen den Patches innerhalb jeder Dichtestufe
Daten
![]()
'data.frame': 80 obs. of 4 variables:
$ Treatment: int 100 100 100 100 100 100 100 100 100 100 ...
$ Patch : int 1 1 1 1 1 2 2 2 2 2 ...
$ Quadrat : int 1 2 3 4 5 1 2 3 4 5 ...
$ Algae : int 0 0 0 6 2 0 0 0 0 0 ...Beide Faktoren müssen in R als Faktor definiert sein. Der verschachtelte Faktor (hier ‘Patch’) muss für jede Stufe eine einzigartige ID haben!
LME | Seeigeleffekt - FG-Prüfung
![]()
Prüfen der Freiheitsgrade für ‘Treatment’:
- N: 16 (EUs: Patches)
- n: 5 (Quadrate als Replikate pro Patch)
- p: 4 (Seeigeldichten)
\begin{align*} \text{Algae} &= \text{Treatment} + \text{Fehler}\\ \text{(N - 1)} &= \text{(p - 1)} + \text{(N - p)}\\ \text{(15)} &= \text{(3)} + \text{(12)} \end{align*}
LME | Seeigeleffekt - Interpretation
![]()
- Es gibt keinen signifikanten Effekt der Seeigeldichte auf die prozentuale Bedeckung der Fadenalgen (F_{3,12} = 2.72, p=0.09).
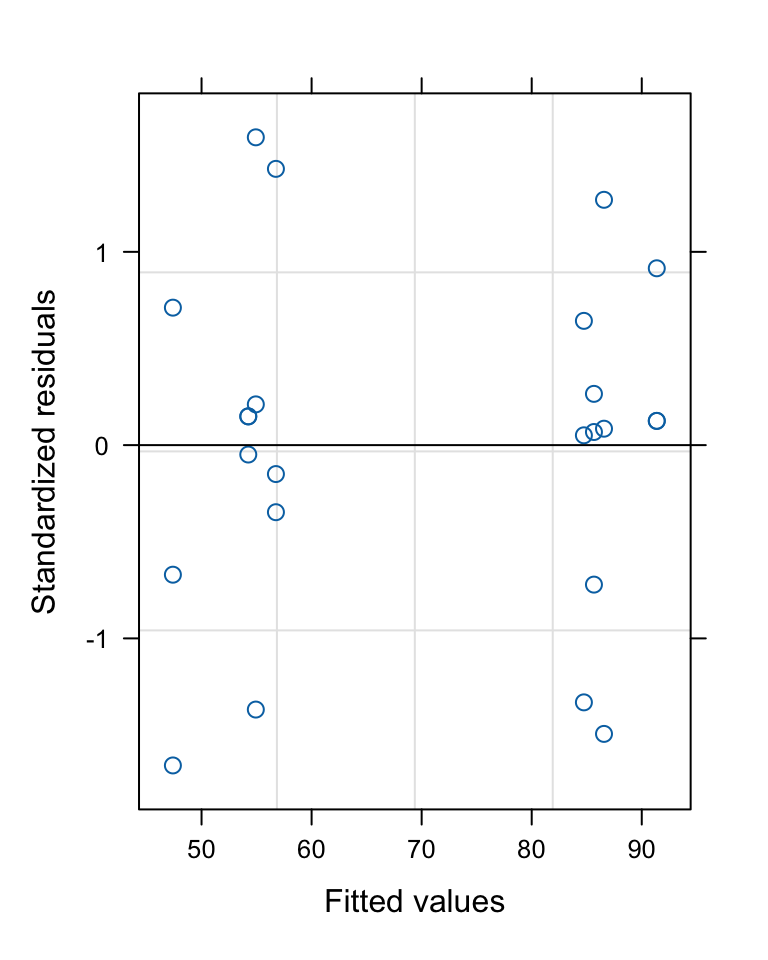
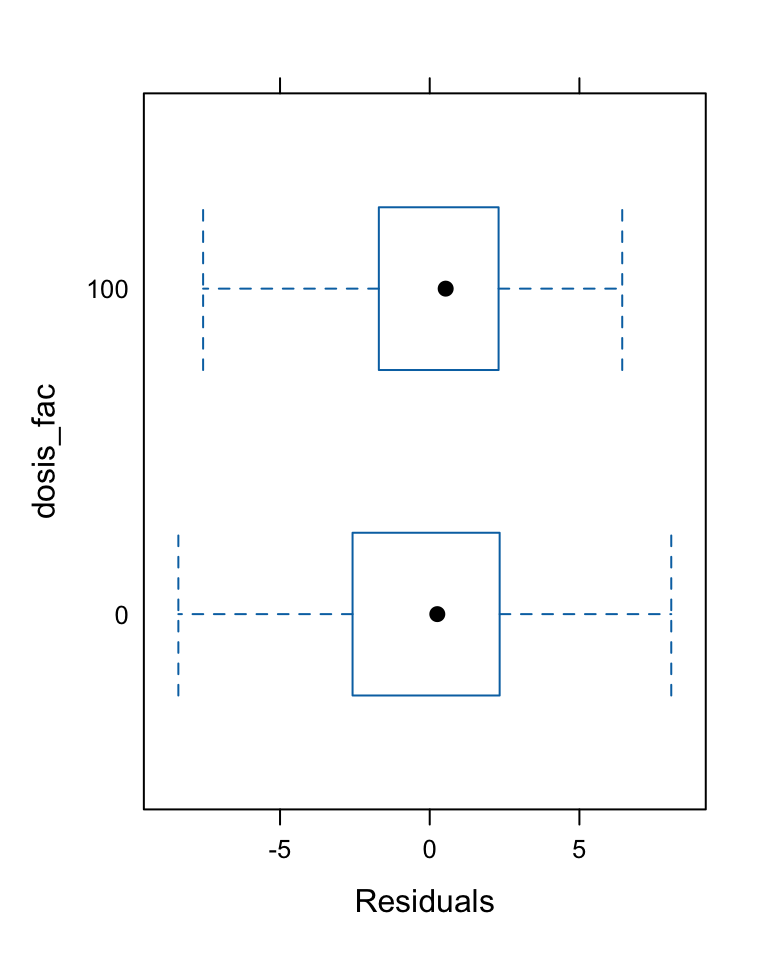
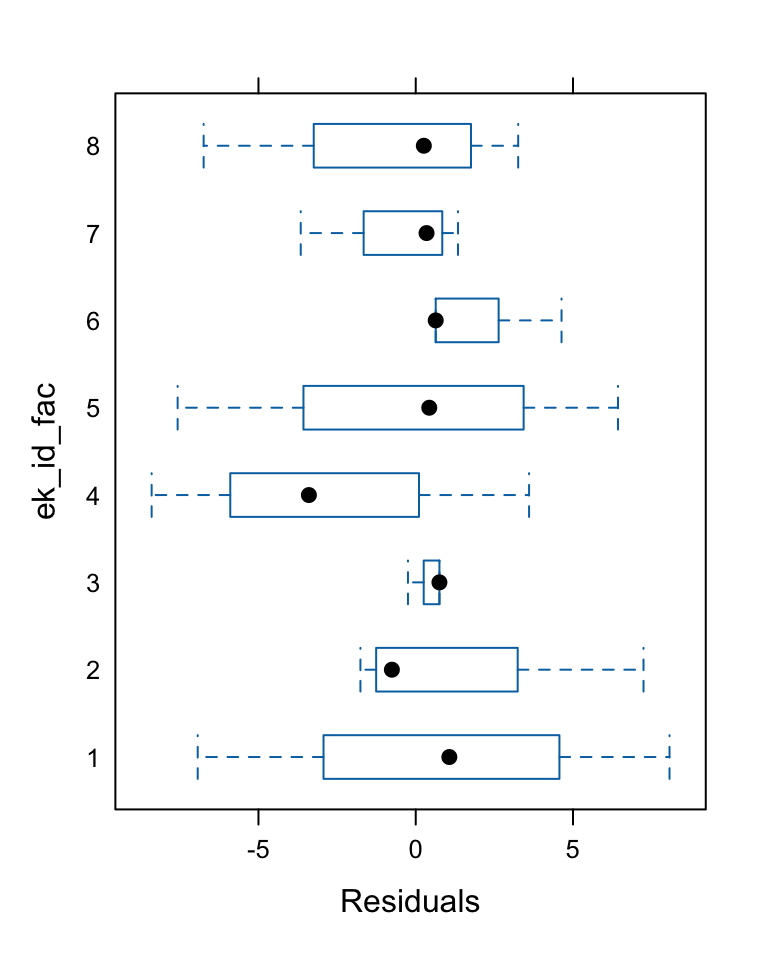
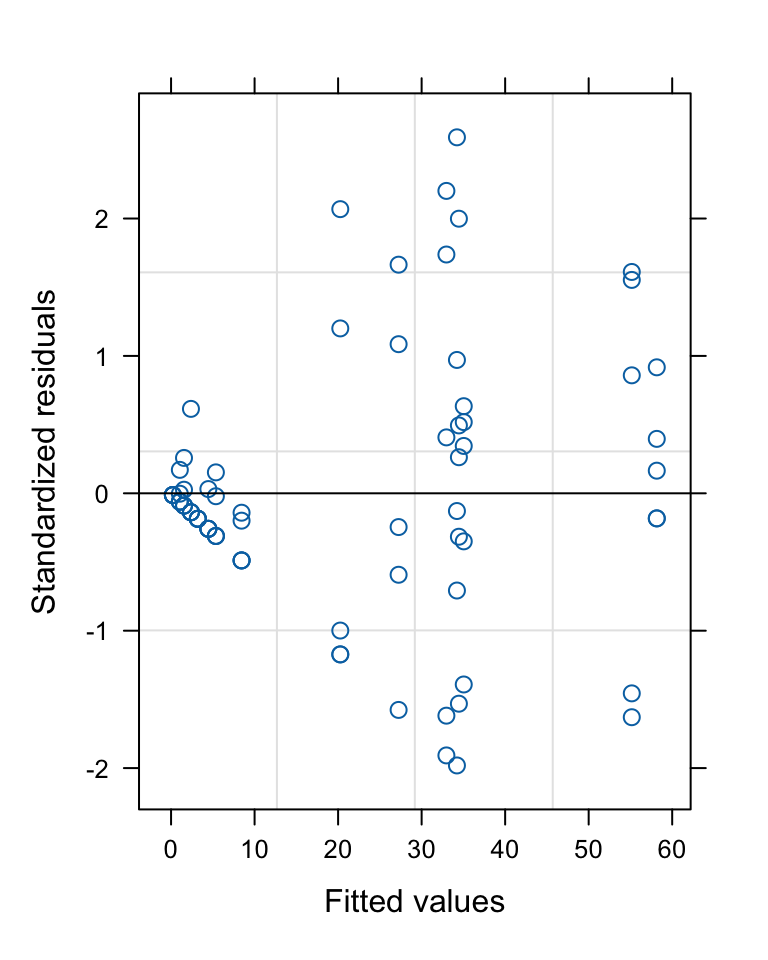
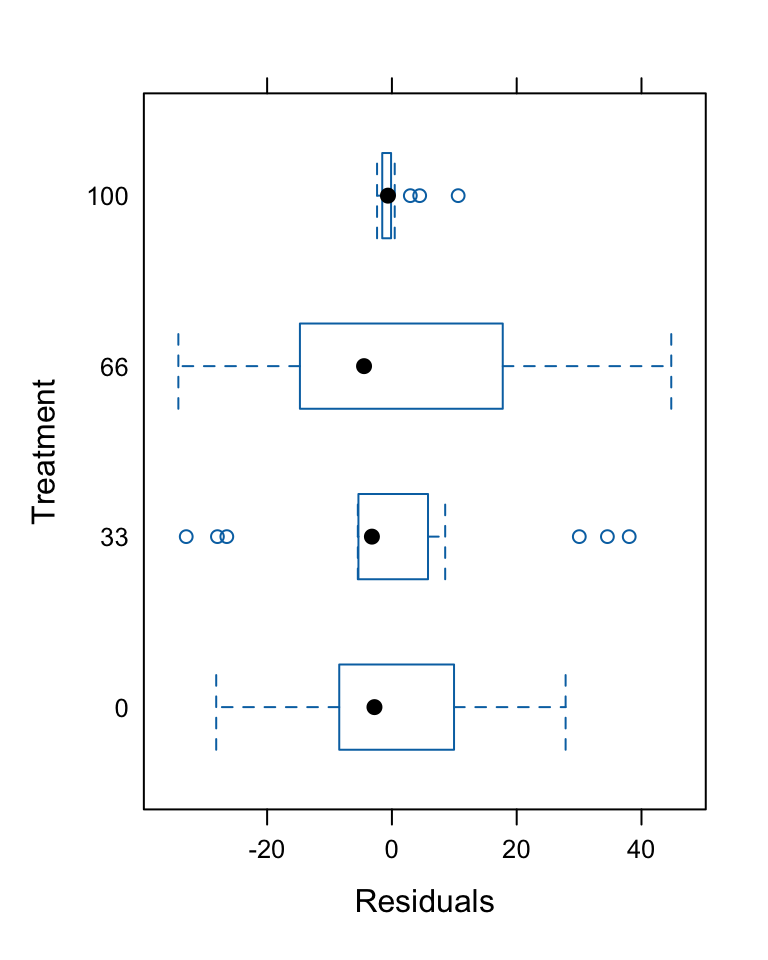
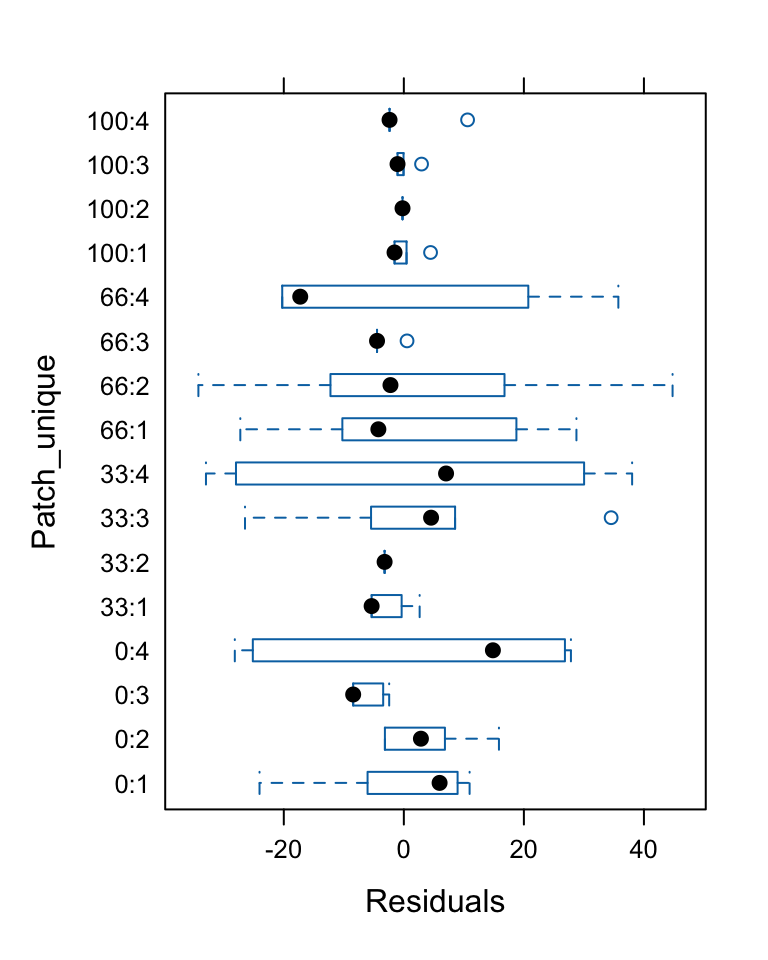
Modelldiagnostik
![]()
→ Die Verteilung sieht nicht gut aus. Lösung: Transformation oder ein anderes Modellierungsverfahren.
Visualisierung der festen und zufälligen Effekte
![]()
Code
# Vorhersagen für feste und zufällige Effekte berechnen
sea_urchins$predictions_fixed <- predict(lme_sea_urchins, level = 0) # nur feste Effekte
sea_urchins$predictions_total <- predict(lme_sea_urchins, level = 1) # feste+zufällige Effekte
ggplot(sea_urchins, aes(x = Treatment)) +
# Beobachtungspunkte + Patch-spezifische Effekte (erste Farbskala)
geom_jitter(aes(y = Algae, colour = Patch), size = 2, width = 0.05, alpha = 0.99) +
geom_point(aes(y = predictions_total, colour = Patch), size = 4, shape = 8) +
scale_colour_brewer(palette = "Set1",
name = "Zufälliger Effekt der Patches (hier gleich kodiert)") +
# neue Farbskala für die fixe Komponente (Seeigeldichte)
ggnewscale::new_scale_color() +
# Linie für die nur-festen Effekte (zweite Farbskala)
geom_point(aes(y = predictions_fixed,
colour = "Fester Effekt der Seeigeldichte"),
size = 5, shape = 0) +
scale_colour_manual(
name = "Modellkomponente",
values = c("Fester Effekt der Seeigeldichte" = "black"),
guide = guide_legend(override.aes = list(size = 5, shape = 0))
) +
# Layout
labs(y = "Algenbedeckung ( in %)", x = "Seeigeldichte") +
theme_bw(base_size = 15) +
theme(legend.position = "bottom", legend.box = "vertical")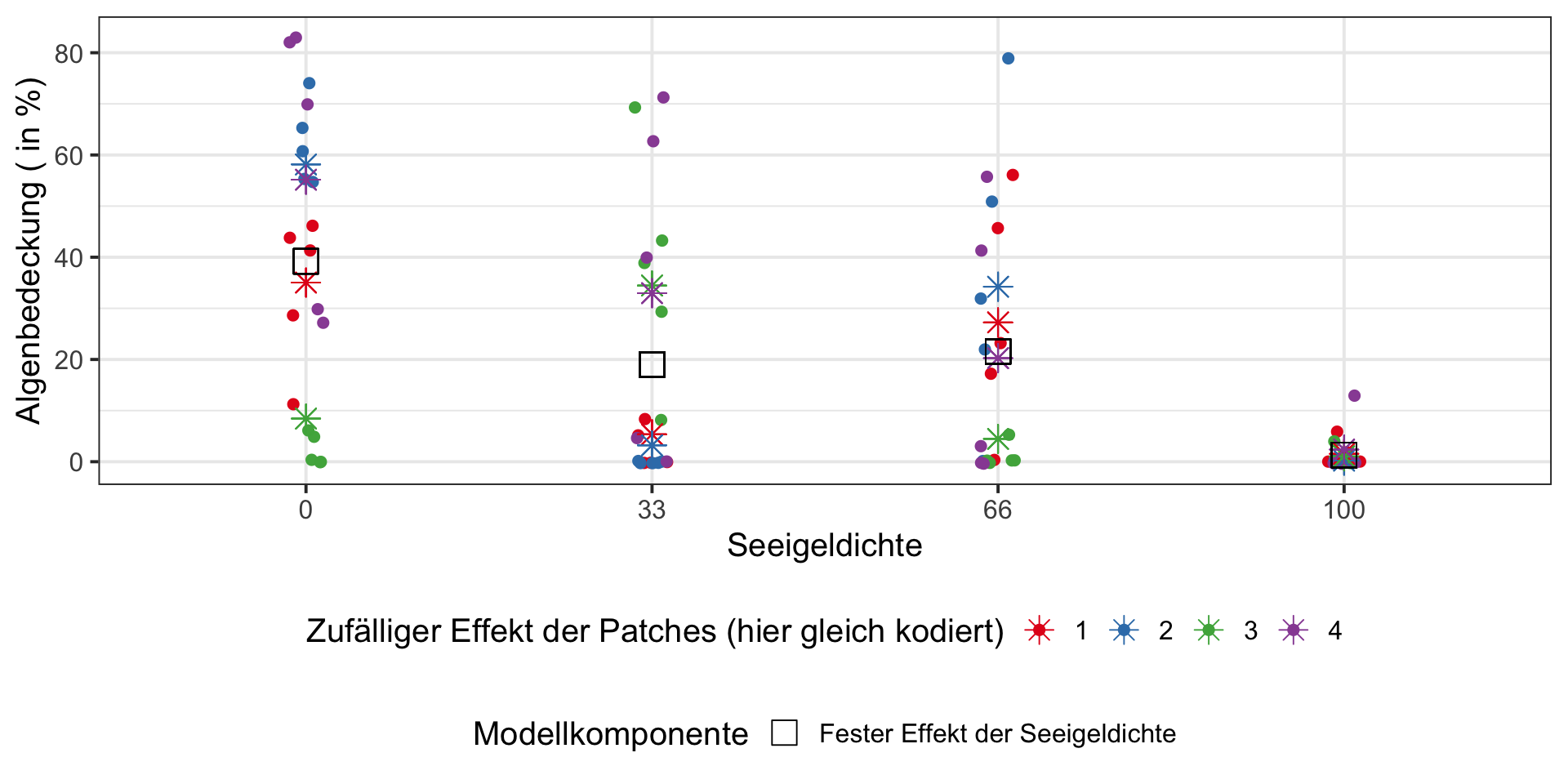
Varianz-Komponenten
![]()
Berechnung der prozentualen Varianzkomponenten in der zufälligen Komponente:
Patch_unique = pdLogChol(1)
Variance StdDev
(Intercept) 294.3125 17.15554
Residual 298.6000 17.28005- → Von der zufälligen Variation entfällt 49.7% auf die unterschiedlichen Patches innerhalb der Dichtestufen.
Praxisbeispiel 2:
3-faktorielles Design mit 2 verschachtelten Faktoren
![]()
Glykogengehalt in Rattenlebern
![]()
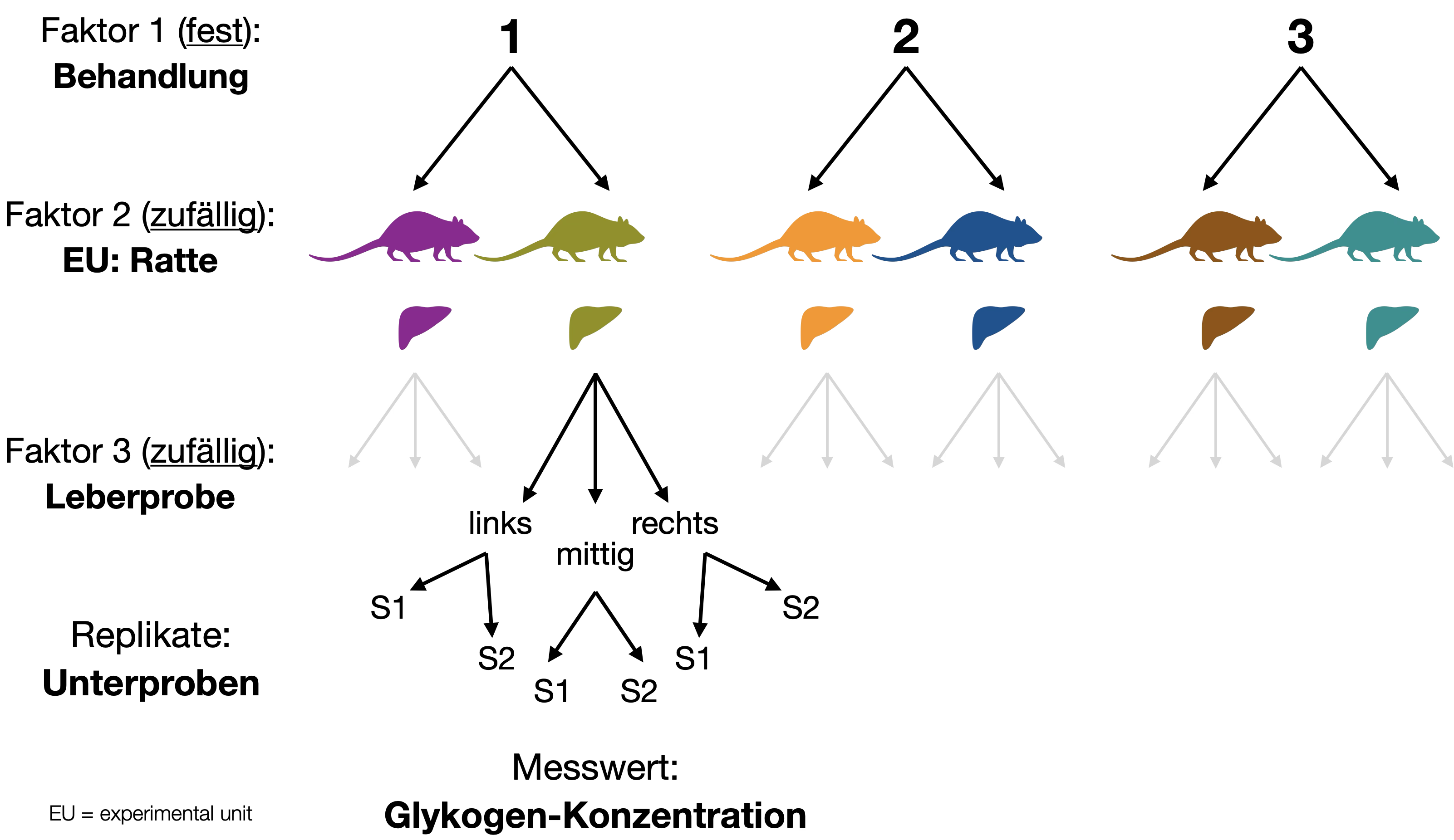
Beispiel aus Sokal & Rohlf (1995): Biometry.
WH Freeman and Co., New York, NY.
- Sechs Ratten wurden zufällig auf drei Behandlungsbedingungen verteilt (zwei Ratten pro Bedingung).
- Ihre Lebern wurden in drei Stücke geteilt, und auf jedem Stück wurden zwei Messungen durchgeführt, was zu 6 x 3 x 2 = 36 Beobachtungen führte.
- Die Ratten sind die experimentellen Einheiten, und es gibt zwei Ebenen der Unterstichprobenahme (Subsampling).
Daten
![]()
'data.frame': 36 obs. of 4 variables:
$ Glycogen : int 131 130 131 125 136 142 150 148 140 143 ...
$ Treatment: int 1 1 1 1 1 1 1 1 1 1 ...
$ Rat : int 1 1 1 1 1 1 2 2 2 2 ...
$ Liver : int 1 1 2 2 3 3 1 1 2 2 ...‘Summary Measure’ Analysis
![]()
Pseudoreplikation wird durch Mittelung berücksichtigt:
LME
![]()
lme_glycogen <- lme(
fixed = Glycogen ~ Treatment,
random = ~ 1 | Rat_unique/Liver_unique,
data = glycogen
)
anova(lme_glycogen) numDF denDF F-value p-value
(Intercept) 1 18 2738.654 <.0001
Treatment 2 3 2.929 0.1971- Wir erhalten für den Haupteffekt (‘Treatment’) das gleiche Ergebnis wie bei einer einfachen ANOVA mit den Mittelwerten.
- Laut dem Modell gibt es keinen signifikanten Behandlungseffekt (F_{2,3} = 2.9, p > 0.05).
LME | Varianz-Komponenten 1
![]()
Variance StdDev
Rat_unique = pdLogChol(1)
(Intercept) 36.06482 6.005399
Liver_unique = pdLogChol(1)
(Intercept) 14.16667 3.763863
Residual 21.16667 4.600725[1] 50.51191 19.84201 29.64607- Ratten innerhalb von Behandlungen: 50.5%
- Leberstücke innerhalb von Ratten innerhalb von Behandlungen: 19.8%
- Residuen = Präparate innerhalb von Leberstücken: 29.6%
LME | Varianz-Komponenten 1
![]()
Variance StdDev
Rat_unique = pdLogChol(1)
(Intercept) 36.06482 6.005399
Liver_unique = pdLogChol(1)
(Intercept) 14.16667 3.763863
Residual 21.16667 4.600725[1] 50.51191 19.84201 29.64607Konsequenz für zukünftige Experimente
- → Mehr als 50 % der zufälligen Variation wird durch Unterschiede zwischen den Ratten erklärt.
- → Es wäre deutlich sinnvoller, das Experiment mit mehr als sechs Ratten zu wiederholen, anstatt die Lebern in noch mehr Stücke zu zerteilen.
Praxisbeispiel 3:
LME mit 1 festen Kovariate und 1 zufälligen Faktor
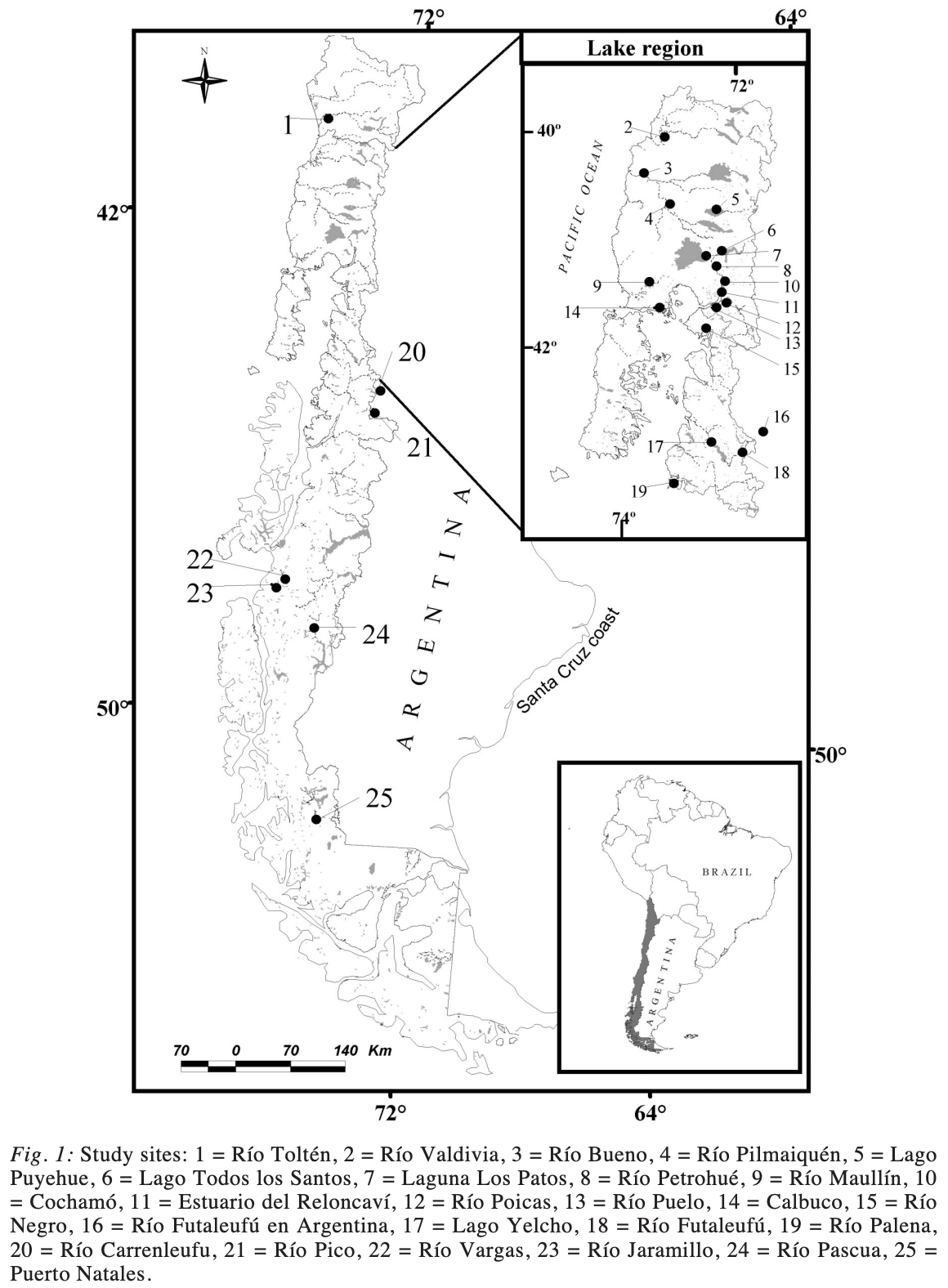
Längen-Gewichts-Beziehung bei Königslachsen

- In der letzten Vorlesung haben wir im Rahmen einer ANCOVA den Faktor ‘location’ als festen Faktor behandelt, da wir daran interessiert waren, gezielt Unterschiede zwischen diesen spezifischen Orten zu untersuchen.
- Alternativ könnten wir die Orte auch als zufälligen Faktor behandeln.
- Dies wäre sinnvoll, wenn wir die Orte als eine zufällige Auswahl aus einer größeren Anzahl potenzieller Standorte betrachten, an denen Königslachse vorkommen.
- Es würde uns ermöglichen, Aussagen über die allgemeine Variabilität der Längen-Gewichts-Beziehungen zwischen unterschiedlichen Standorten zu treffen, anstatt nur spezifisch für die ausgewählten drei Orte.
ANCOVA

![]()
Call:
lm(formula = w_ln ~ tl_ln + loc, data = ChinookArg)
Residuals:
Min 1Q Median 3Q Max
-0.60633 -0.19351 -0.00076 0.14352 1.61286
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -8.12169 0.56827 -14.292 < 2e-16 ***
tl_ln 2.30492 0.12563 18.347 < 2e-16 ***
locPetrohue -0.22813 0.08013 -2.847 0.00528 **
locPuyehue -0.45699 0.09231 -4.951 2.74e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.3186 on 108 degrees of freedom
Multiple R-squared: 0.8962, Adjusted R-squared: 0.8934
F-statistic: 311 on 3 and 108 DF, p-value: < 2.2e-16‘Random Intercept’ Modell

![]()
chinook_lme1 <- lme(fixed = w_ln ~ tl_ln, random = ~1 | loc, data = ChinookArg)
summary(chinook_lme1)Linear mixed-effects model fit by REML
Data: ChinookArg
AIC BIC logLik
80.97081 91.77273 -36.48541
Random effects:
Formula: ~1 | loc
(Intercept) Residual
StdDev: 0.2187328 0.318637
Fixed effects: w_ln ~ tl_ln
Value Std.Error DF t-value p-value
(Intercept) -8.490223 0.5502014 108 -15.43112 0
tl_ln 2.336738 0.1225207 108 19.07218 0
Correlation:
(Intr)
tl_ln -0.972
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-1.8743469 -0.6029318 0.0192709 0.4386401 5.0896512
Number of Observations: 112
Number of Groups: 3 ‘Random Intercept and Slope’ Modell

![]()
chinook_lme2 <- lme(fixed = w_ln ~ tl_ln, random = ~tl_ln | loc, data = ChinookArg)
summary(chinook_lme2)Linear mixed-effects model fit by REML
Data: ChinookArg
AIC BIC logLik
84.97081 101.1737 -36.48541
Random effects:
Formula: ~tl_ln | loc
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
(Intercept) 2.187328e-01 (Intr)
tl_ln 3.504195e-05 -0.001
Residual 3.186370e-01
Fixed effects: w_ln ~ tl_ln
Value Std.Error DF t-value p-value
(Intercept) -8.490223 0.5502014 108 -15.43112 0
tl_ln 2.336738 0.1225207 108 19.07218 0
Correlation:
(Intr)
tl_ln -0.972
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-1.8743469 -0.6029318 0.0192709 0.4386401 5.0896512
Number of Observations: 112
Number of Groups: 3 Grafischer Vergleich

Code
ChinookArg <- ChinookArg |>
mutate(
pred_ancova = predict(chinook_ancova),
pred_lme1_fixed = predict(chinook_lme1, level = 0),
pred_lme1_total = predict(chinook_lme1, level = 1)
)
# ANCOVA
p1 <- ggplot(ChinookArg, aes(x = tl_ln, y = w_ln, colour = loc)) +
geom_point() +
scale_colour_manual(values =
c("forestgreen", "orange1", "deeppink4")) +
guides(colour = "none") +
geom_line(aes(x = tl_ln, y = pred_ancova), linewidth = 1.1) +
labs(x = "ln(Länge)", y = "ln(Gewicht)",
title = "ANCOVA-Modell")
# LME1
p2 <- ggplot(ChinookArg, aes(x = tl_ln, y = w_ln, colour = loc)) +
geom_point() +
scale_colour_manual(values =
c("forestgreen", "orange1", "deeppink4")) +
guides(colour = "none") +
geom_line(aes(x = tl_ln, y = pred_lme1_fixed), colour = "black", linewidth=2) +
geom_line(aes(x = tl_ln, y = pred_lme1_total)) +
labs(x = "ln(Länge)", y = "ln(Gewicht)",
title = "LME (Random Intercept-Modell)")
gridExtra::grid.arrange(p1, p2, nrow = 1)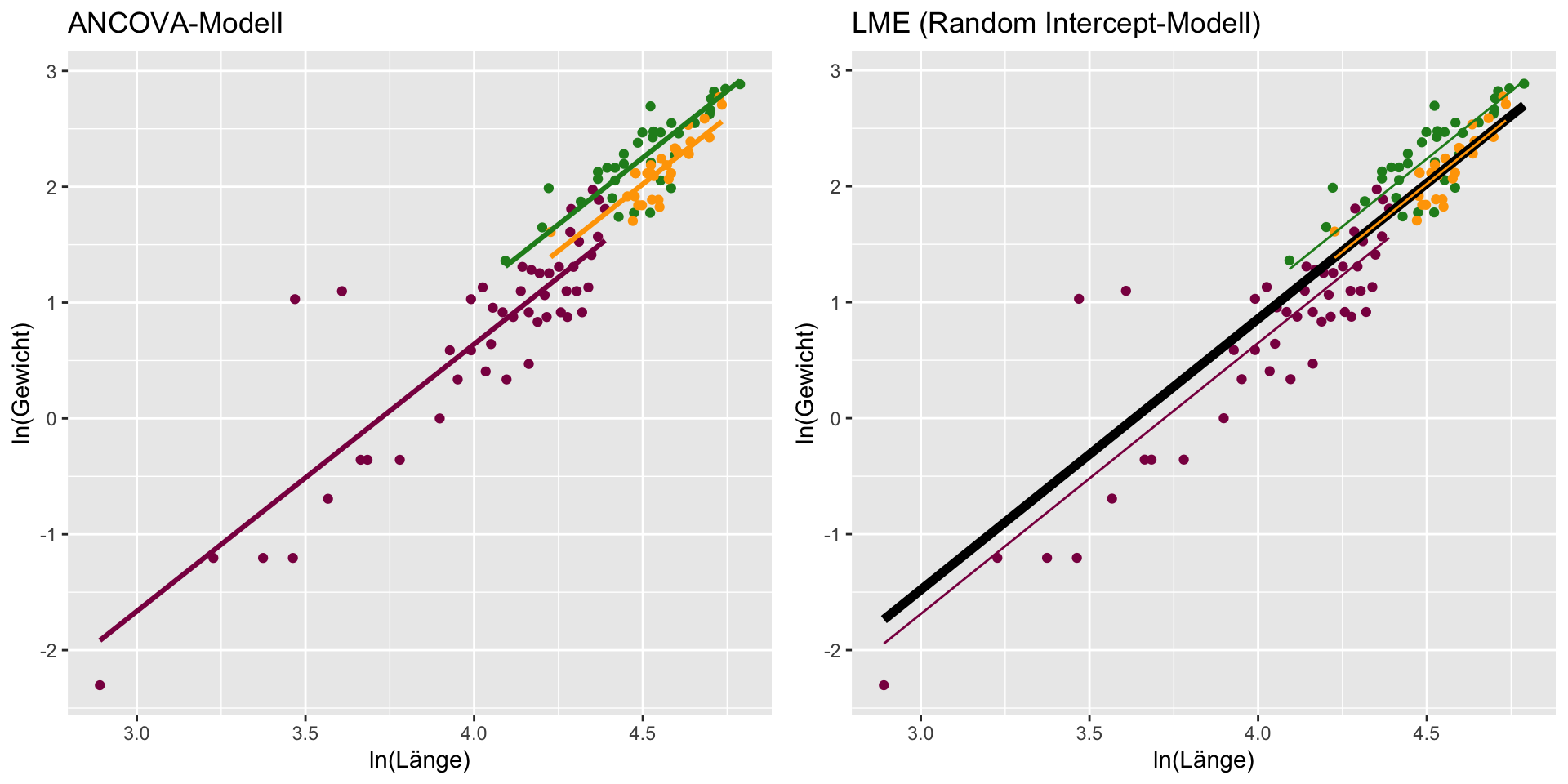
Modellvorhersage | ‘Random Intercept’ Modell

Modellvorhersage | ‘Random Intercept and Slope’ Modell

Your turn …
![]()
05:00
LME mit dem iris Datensatz
![]()
- In der ANCOVA-Vorlesung haben wir im Übungsquiz
Speciesals festen Faktor behandelt. - Nun wollen wir vergleichen, wie der Einfluss der Blattlänge ist, wenn
Speciesals zufälliger Effekt behandelt wird.
- Da die Interaktion mit Petal.Length nicht signifikant war, wollen wir ein Random Intercept-LME erstellen.
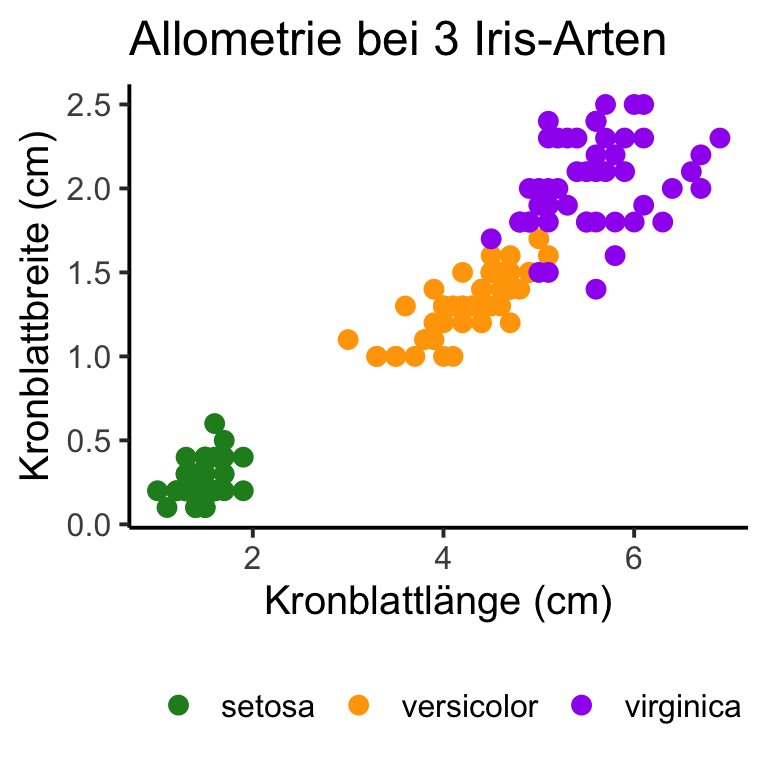
Analysis of Variance Table
Response: Petal.Width
Df Sum Sq Mean Sq F value Pr(>F)
Petal.Length 1 80.260 80.260 2487.017 < 2.2e-16 ***
Species 2 1.598 0.799 24.766 5.482e-10 ***
Residuals 146 4.712 0.032
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Quiz 1 | R Code Modellierung & Output
![]()
Quiz 2 | Interpretation: Feste Effekte
![]()
numDF denDF F-value p-value
(Intercept) 1 146 26.89443 <.0001
Petal.Length 1 146 52.72039 <.0001Linear mixed-effects model fit by REML
Data: iris
AIC BIC logLik
-60.69384 -48.70499 34.34692
Random effects:
Formula: ~1 | Species
(Intercept) Residual
StdDev: 0.3997549 0.1796796
Fixed effects: Petal.Width ~ Petal.Length
Value Std.Error DF t-value p-value
(Intercept) 0.2886165 0.26308813 146 1.097033 0.2744
Petal.Length 0.2423408 0.03337623 146 7.260881 0.0000
Correlation:
(Intr)
Petal.Length -0.477
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-3.53994212 -0.45102711 -0.06366546 0.52292901 2.69989100
Number of Observations: 150
Number of Groups: 3 Quiz 3 | Interpretation: Zufallseffekte
![]()
numDF denDF F-value p-value
(Intercept) 1 146 26.89443 <.0001
Petal.Length 1 146 52.72039 <.0001Linear mixed-effects model fit by REML
Data: iris
AIC BIC logLik
-60.69384 -48.70499 34.34692
Random effects:
Formula: ~1 | Species
(Intercept) Residual
StdDev: 0.3997549 0.1796796
Fixed effects: Petal.Width ~ Petal.Length
Value Std.Error DF t-value p-value
(Intercept) 0.2886165 0.26308813 146 1.097033 0.2744
Petal.Length 0.2423408 0.03337623 146 7.260881 0.0000
Correlation:
(Intr)
Petal.Length -0.477
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-3.53994212 -0.45102711 -0.06366546 0.52292901 2.69989100
Number of Observations: 150
Number of Groups: 3 Quiz 4 | Modellvorhersage
![]()
Schauen Sie sich die geschätzten Koeffizienten des LME an. Wie lautet die Regressionsgleichung für die Art I. versicolor?
Modellvergleich
![]()
Call:
lm(formula = Petal.Width ~ Petal.Length + Species, data = iris)
Residuals:
Min 1Q Median 3Q Max
-0.63706 -0.07779 -0.01218 0.09829 0.47814
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.09083 0.05639 -1.611 0.109
Petal.Length 0.23039 0.03443 6.691 4.41e-10 ***
Speciesversicolor 0.43537 0.10282 4.234 4.04e-05 ***
Speciesvirginica 0.83771 0.14533 5.764 4.71e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1796 on 146 degrees of freedom
Multiple R-squared: 0.9456, Adjusted R-squared: 0.9445
F-statistic: 845.5 on 3 and 146 DF, p-value: < 2.2e-16Linear mixed-effects model fit by REML
Data: iris
AIC BIC logLik
-60.69384 -48.70499 34.34692
Random effects:
Formula: ~1 | Species
(Intercept) Residual
StdDev: 0.3997549 0.1796796
Fixed effects: Petal.Width ~ Petal.Length
Value Std.Error DF t-value p-value
(Intercept) 0.2886165 0.26308813 146 1.097033 0.2744
Petal.Length 0.2423408 0.03337623 146 7.260881 0.0000
Correlation:
(Intr)
Petal.Length -0.477
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-3.53994212 -0.45102711 -0.06366546 0.52292901 2.69989100
Number of Observations: 150
Number of Groups: 3 Quiz 5 | Vergleich mit ANCOVA 1
![]()
Quiz 6 | Vergleich mit ANCOVA 2
![]()
Übungen
Übungswoche 4
![]()
Revision der DS2 Fallstudien-Analysen als LME
Vorbereitung @home
- Bevor Sie in der Übungsstunde die in der Vorlesung vorgestellten Lösungen zur Analyse einer ANOVA mit einem komplex verschachtelten Design anwenden, sollen Sie sich mit ChatGPT (z.B. über https://uhhgpt.uni-hamburg.de/) als unterstützendem Werkzeug zur Datenanalyse vertraut machen.
- Beantworten Sie vor der vierten Übungsstunde die Fragen zu linearen gemischten Modellen (LMEs) im Moodle-Quiz.
Fragen..??

Total konfus?

Buchkapitel zum Nachlesen
- The R Book von M.J. Crawley:
- Kapitel 11.3 Pseudoreplication: Nested designs and split plots
- Kapitel 19 Mixed-Effect Models
- Experimental Design and Data Analysis for Biologists von G.P. Quinn & M.J. Keough:
- Kapitel 9.1 Nested (hierarchical) designs
Total gelangweilt?

Dann testen Sie doch Ihr Wissen in folgendem Abschlussquiz…
Abschlussquiz
![]()

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de

Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.
Kurswebseite: Data Science 3