2-faktorielle Varianzanalyse: verschachteltes Design

DS3 - Explorative Datenanalyse & Data Mining

Saskia Otto

Universität Hamburg, IMF

Wintersemester 2023/2024

Lernziele

Am Ende dieser VL- und Übungseinheit werden Sie

  • wissen, wie pseudoreplizierte Daten und Daten von verschachtelten bzw. hierarchischen Designs mithilfe einer Varianzanalyse analysiert werden können.
  • eine alternative, bessere Variante zur Analyse der Fallstudiedaten (aus DS2) durchführen können..
  • wissen, wie feste und zufällige Faktoren in die Berechnung der F-Werte einfließen
  • 3 Varianten zur Berechnung einer mehrfaktoriellen, verschachtelten ANOVA kennen.

2-faktorielle Varianzanalyse mit verschachtelten Faktoren
-Theorie

Verschachtelte (hierarchische) Designs

  • In der Ökologie wird Pseudoreplikation oft verursacht durch fehlende Replikation auf der richtigen Ebene des experimentellen Designs.
  • Subsampling kann hier hilfreich sein.
  • Häufig: ‘nested ANOVA’ mit zwei Faktoren
    • Faktor A mit p Gruppen oder Stufen → fest oder zufällig, aber normalerweise fest
    • Faktor B mit q Gruppen oder Ebenen innerhalb jeder Ebene von A (die Unterprobe) → in der Regel zufällig

Einfluss der Seeigelbeweidung im Korallenriff

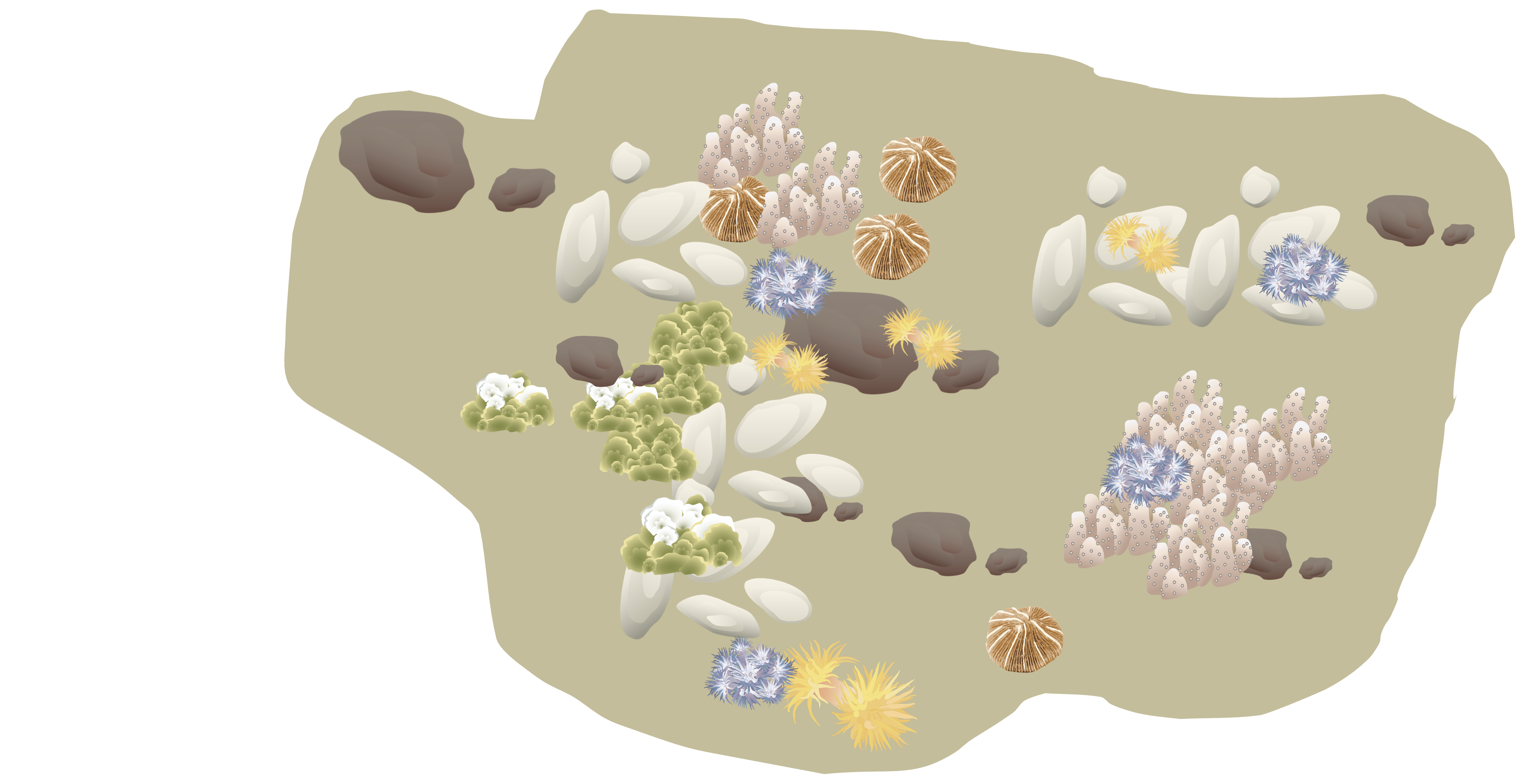
Beispiel ist aus Kapitel 9.1 in Quinn & Keough (2002): Experimental Design and Data Analysis for Biologists



  • Andrew & Underwood (1993) manipulierten die Dichte von Seeigeln in der flachen subtidalen Region eines Standorts in der Nähe von Sydney, um die Auswirkungen auf den prozentualen Bewuchs mit Fadenalgen zu testen.
  • Es gab vier Seeigelbehandlungen: keine Seeigel, 33% der ursprünglichen Dichte, 66% der ursprünglichen Dichte und 100% der ursprünglichen Dichte.
  • Die Behandlungen wurden an vier verschiedenen Stellen (3-4 m^2 Flächen) pro Behandlung wiederholt, und der prozentuale Bewuchs mit Fadenalgen (Antwortvariable) wurde in fünf zufälligen Quadraten pro Stelle gemessen.
  • Es handelt sich somit um ein verschachteltes Design mit Behandlung (fester Faktor), Stellen (im Engl. ‘patches’) innerhalb der Behandlung (zufälliger Faktor) und Quadraten als Replikate.

Seeigelbeweidung im Korallenriff

Das Design

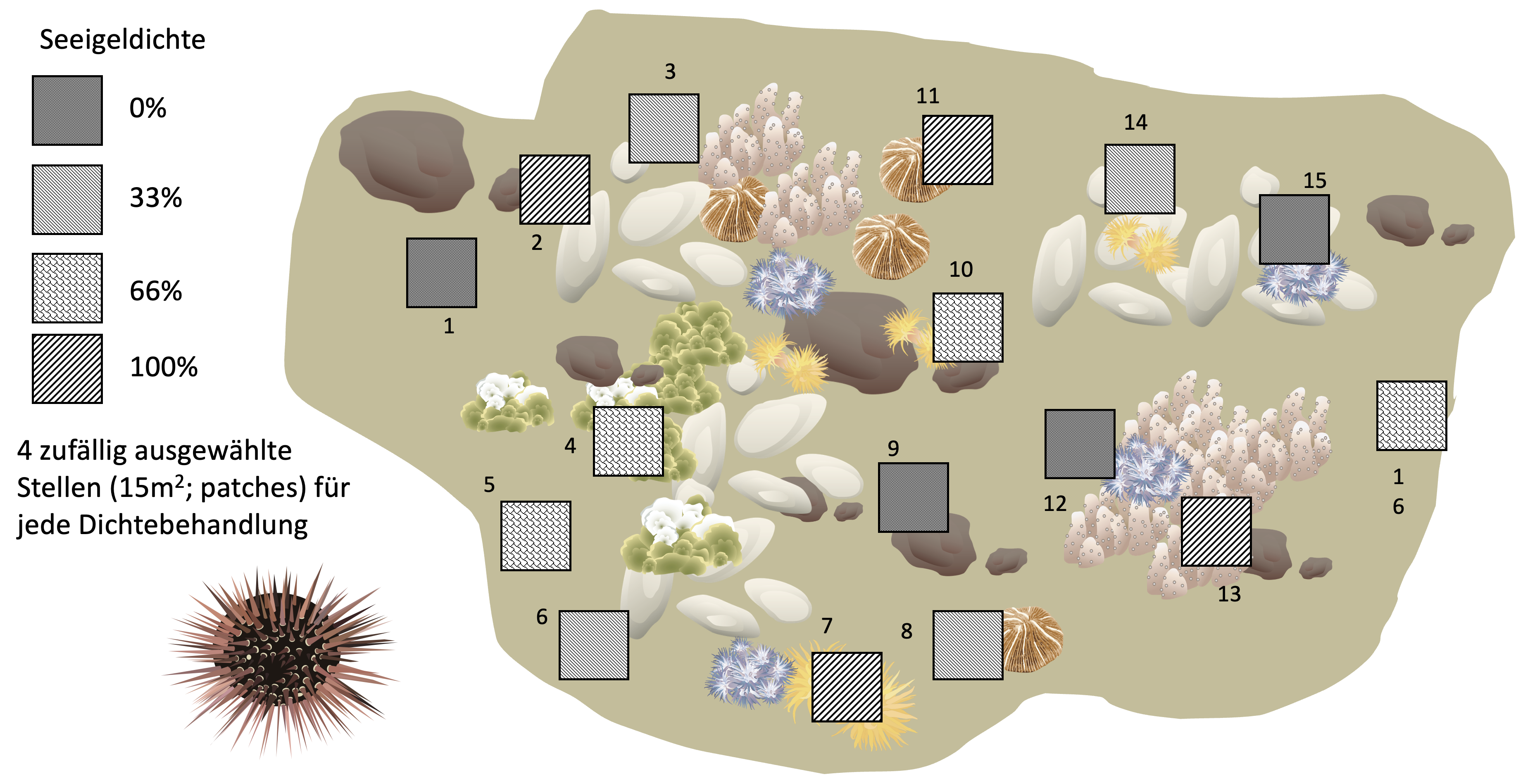
Antwortvariable Y: % Bewuchs mit Fadenalgen

  • Jeder Patch (15 m^2) ist zu groß, um ihn zu erfassen ➜ 5 Quadrate (3-4 m^2) als Unterprobe
  • Patches werden zu Faktor B innerhalb von Faktor A
  • Rest: 5 Wiederholungsquadrate in jedem Patch innerhalb jeder Dichtestufe

Lineares ANOVA Model

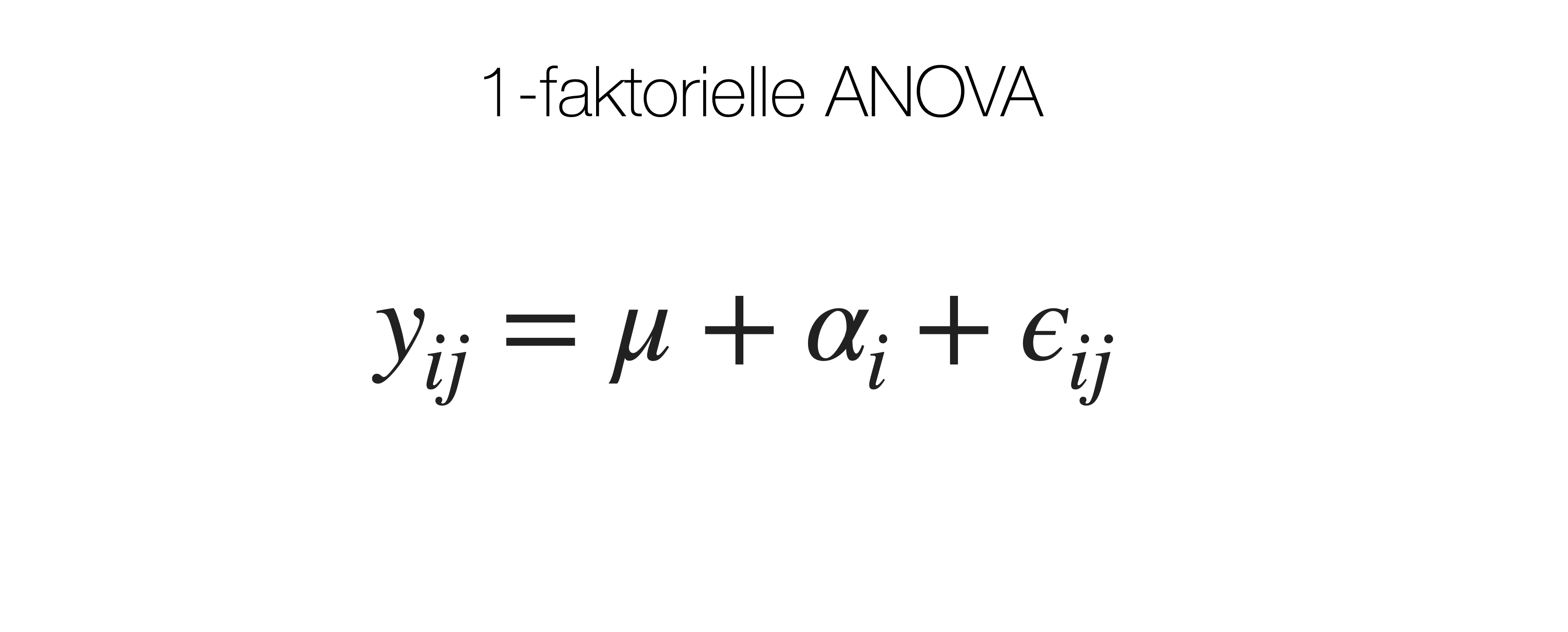
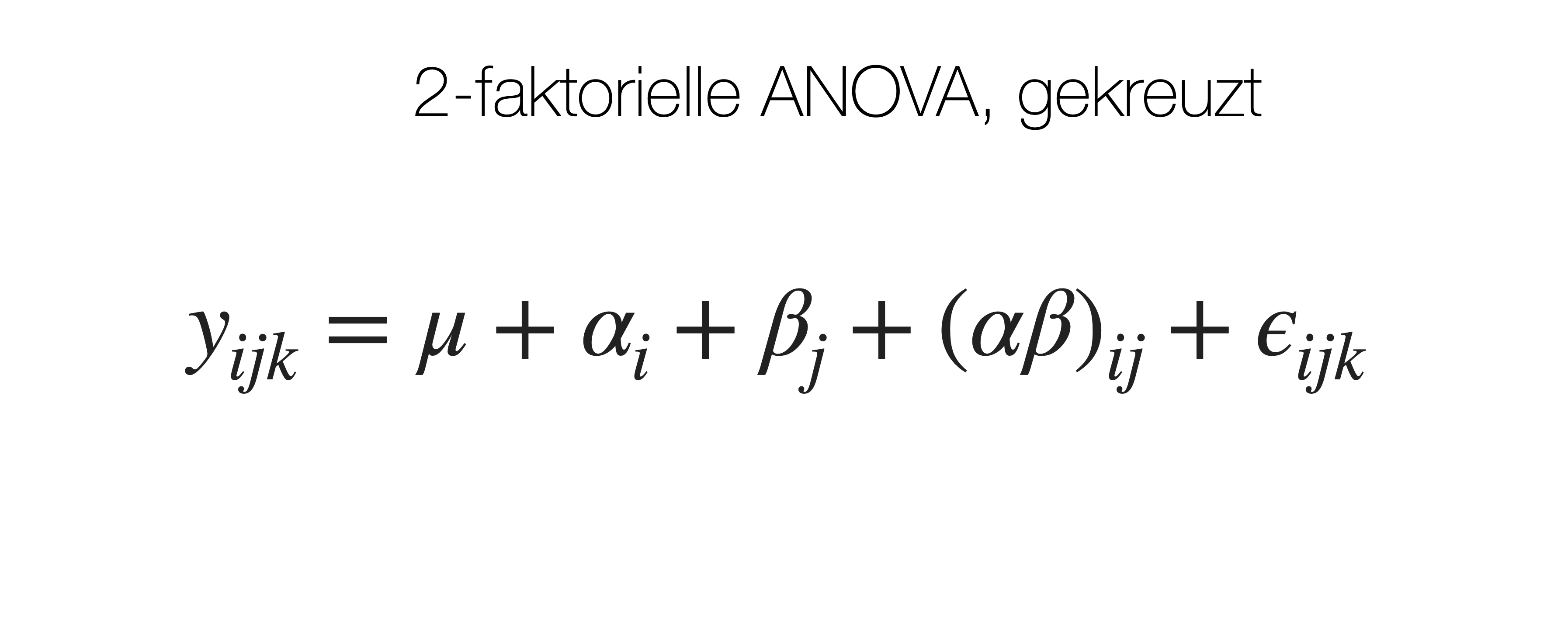
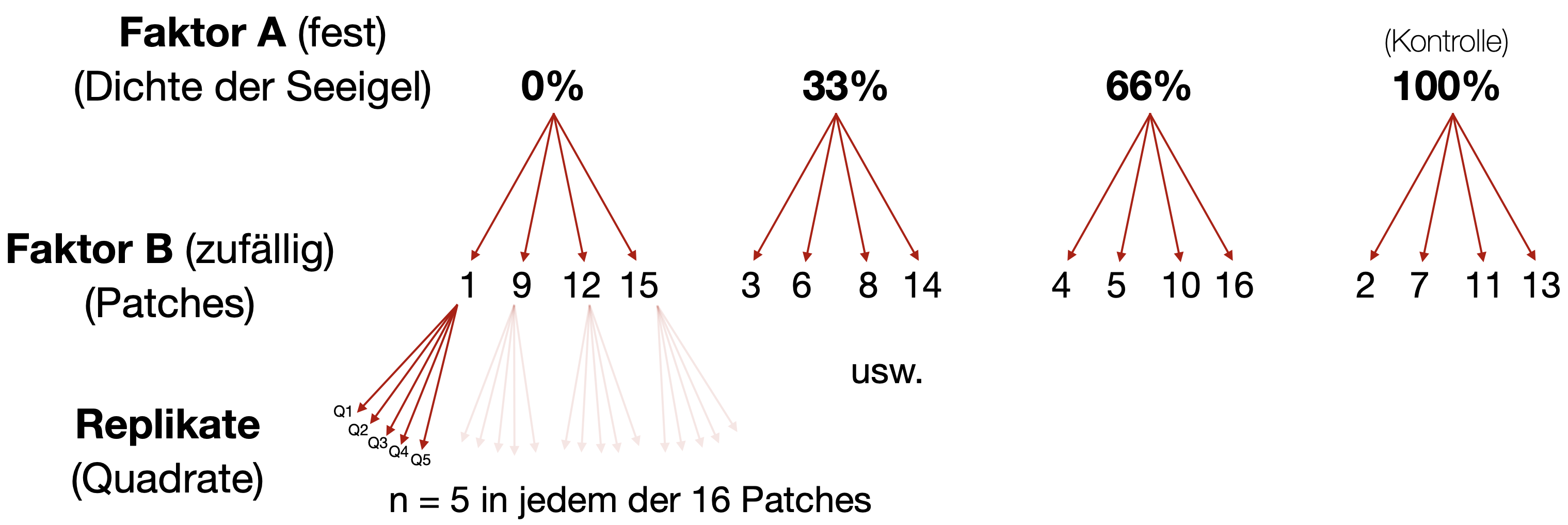
In unserem Beispiel ist

  • i = Dichtestufe 1,..,p (p=4 hier) (Faktor A)
  • j = Patches 1,..,q (q=4 hier) in jeder Gruppe von p (Faktor B)
  • k = Replikate 1,..,n (n=5 hier)

\text{(% Bewuchs Fadenalgen)} = \mu + \text{(Seeigeldichte)}_i + \text{(Patch innerhalb der Seeigeldichte)}_{j(i)} + \epsilon_{ijk}

Hypothesen

Wir wollen nun 2 Hypothesen testen

Faktor A - H0_A: \alpha_1 = \alpha_2 = .. \alpha_i = 0

  • → d.h. es gibt keinen Unterschied in der durchschnittlichen Menge an Fadenalgen zwischen den vier Seeigeldichte-Behandlungen

Faktor B - H0_B: \sigma_{\beta}^2 = 0

  • → d.h. es gibt keine signifikante Variabilität zwischen den Patches innerhalb jeder Dichtestufe

Varianzzerlegung

ANOVA Tabelle

Berechnung der F-Werte

Interpretation der Ergebnisse

\Rightarrow Die H0_A kann nicht abgelehnt werden: es gibt keine signifikanten Unterschiede in der Menge der Fadenalgen zwischen den verschiedenen Dichtestufen.

\Rightarrow Die H0_B kann abgelehnt werden: es gibt sign. Unterschiede zwischen den Patches innerhalb jeder Dichtestufe.

2-faktorielle Varianzanalyse mit verschachtelten Faktoren
-Durchführung in R

Datentyp

Beide Faktoren müssen in R auch als Faktor definiert sein.

Prüfung der Datentypen
str(sea_urchins)
'data.frame':   80 obs. of  4 variables:
 $ Treatment: int  100 100 100 100 100 100 100 100 100 100 ...
 $ Patch    : int  1 1 1 1 1 2 2 2 2 2 ...
 $ Quadrat  : int  1 2 3 4 5 1 2 3 4 5 ...
 $ Algae    : int  0 0 0 6 2 0 0 0 0 0 ...
Konvertierung
sea_urchins <- sea_urchins |>
  mutate(
    Treatment = as.factor(Treatment), 
    Patch = as.factor(Patch)
  )

Codierung

Der verschachtelte Faktor (hier ‘Patch’) muss für jede Stufe eine einzigartige ID haben!

Prüfung der Faktorstufen-IDs
sea_urchins |>
  group_by(Treatment, Patch) |>
  count()
# A tibble: 16 × 3
# Groups:   Treatment, Patch [16]
   Treatment Patch     n
   <fct>     <fct> <int>
 1 0         1         5
 2 0         2         5
 3 0         3         5
 4 0         4         5
 5 33        1         5
 6 33        2         5
 7 33        3         5
 8 33        4         5
 9 66        1         5
10 66        2         5
11 66        3         5
12 66        4         5
13 100       1         5
14 100       2         5
15 100       3         5
16 100       4         5
Neue Faktorstufen-IDs generieren
sea_urchins <- sea_urchins |>
  mutate(Patch_newIDs = as.factor(
    Treatment:Patch))
# A tibble: 16 × 3
# Groups:   Treatment, Patch_newIDs [16]
   Treatment Patch_newIDs     n
   <fct>     <fct>        <int>
 1 0         0:1              5
 2 0         0:2              5
 3 0         0:3              5
 4 0         0:4              5
 5 33        33:1             5
 6 33        33:2             5
 7 33        33:3             5
 8 33        33:4             5
 9 66        66:1             5
10 66        66:2             5
11 66        66:3             5
12 66        66:4             5
13 100       100:1            5
14 100       100:2            5
15 100       100:3            5
16 100       100:4            5

Exploration

Code 
p1 <- sea_urchins |>
  ggplot(aes(x = Treatment, y = Algae, fill = Treatment)) +
  geom_boxplot() +
  guides(fill = "none")
p2 <- sea_urchins |>
  ggplot(aes(x = Patch_newIDs, y = Algae, fill = Treatment)) +
  geom_boxplot() +
  guides(fill = "none")
gridExtra::grid.arrange(p1, p2, nrow = 2)

Durchführung der ANOVA in R

Verschiedene Möglichkeiten

Variante 1

aov() Funktion mit Angabe des verschachtelten (festen) Faktors in der Formel:

aov(y ~ A/B/C)

wobei A/B/C das gleiche ist wie

A + B %in% A + C %in% B %in% A
  • Antwortvariable y
  • Fester Faktor A
  • Der zweite Faktor B ist eingebettet (‘nested’) in A → für R fest
  • Der dritte Faktor C ist eingebettet (‘nested’) in Faktor B, eingebettet in A → für R fest

Variante 2

aov() Funktion mit Angabe des zufälligen (verschachtelten) Faktors in der Formel:

aov(y ~ A + Error(B))

  • fester Faktor A
  • Faktor B wird hier als zufälliger Faktor definiert → bei eindeutigen IDs erkennt R die Verschachtelung automatisch.

Variante 3

Als lineares gemischtes Effektmodell (LME) mit dem R Paket ‘nlme’ (oder ‘lme4’):

nlme:lme(fixed = y ~ a, random = ~1 | b)

fixed:

  • Hier werden die festen, unverschachtelten Faktoren als feste Komponente des Modells definiert. Die Formelschreibweise ist hier wie bekannt.

random:

  • Hier werden die zufälligen, verschachtelten Faktoren definiert.
  • Der Name der Antwortvariable wird in der Zufallskomponente vor dem Tildezeichen weggelassen.
  • Nach dem Achsenabschnitt folgt der vertikale Balken |, der als “bei folgender räumlicher Anordnung der Zufallsvariablen” zu lesen ist.
  • In diesem Beispiel ist Faktor C eingebettet in Faktor B und dieser wiederum in A.

Variante 1

mod_aov1 <- aov(Algae ~ Treatment/Patch_newIDs, sea_urchins)
summary(mod_aov1)
                       Df Sum Sq Mean Sq F value   Pr(>F)    
Treatment               3  14429    4810  16.108 6.58e-08 ***
Treatment:Patch_newIDs 12  21242    1770   5.928 8.32e-07 ***
Residuals              64  19110     299                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Vor- und Nachteile

  • Wir erhalten die vollständige Tabelle bei einem 2-faktoriellen, verschachtelte Design.
  • Aber: da der verschachtelte Faktor als fester Faktor in R interpretiert wird, ist die Berechnung des F-Werts inkorrekt (anstelle der MS_{B(A)} sind im Nenner die MS_{Residuen}) und muss manuell berechnet werden.
  • Wir können die typischen Diagnostikplots erstellen.

Variante 1 | Korrektur

Manuelle Berechnung des F- und p-Werts für Faktor A (Treatment = Seeigeldichte):

correction <- c(
  "F_A korrigiert" = 4810/1770,
  "p-Wert korrigiert" = pf(4810/1770, df1 = 3, df2 = 12, lower.tail = FALSE)
)
correction
   F_A korrigiert p-Wert korrigiert 
       2.71751412        0.09123141

Variante 1 | Modelldiagnostik

par(mfrow = c(2,2))
plot(mod_aov1, which = 1:4)

Hinweis

  • Es gibt klare Anzeichen, dass die Annahme der Varianzhomogenität nicht gegeben ist.
  • Eine Arcus-Sinus- und auch Log-Transformation auf die Prozentdaten haben keine Verbesserung gebracht.
  • Zur Vergleichbarkeit mit dem Originalartikel Andrew & Underwood (1993) und dem Buchkapitel 9.1 in Quinn & Keough (2002) wurde die Demonstration hier mit den untransformierten Daten durchgeführt.

Variante 2

mod_aov2 <- aov(Algae ~ Treatment + Error(Patch_newIDs), sea_urchins)
summary(mod_aov2)

Error: Patch_newIDs
          Df Sum Sq Mean Sq F value Pr(>F)  
Treatment  3  14429    4810   2.717 0.0913 .
Residuals 12  21242    1770                 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Error: Within
          Df Sum Sq Mean Sq F value Pr(>F)
Residuals 64  19110   298.6

Vor- und Nachteile

  • F- und p-Wert für Treatment (Seeigeldichte) sind nun richtig berechnet.
  • Wir erhalten aber keinen F- und p-Wert für unseren verschachtelten Faktor.
  • Wir können keine Modelldiagnostikplots mit plot erstellen oder Residuen mit residuals() direkt ausgeben.

Variante 3 | anova() Output

library(nlme)
mod_lme <- lme(fixed = Algae ~ Treatment, 
  random = ~ 1|Patch_newIDs, data = sea_urchins)

anova(mod_lme)
            numDF denDF   F-value p-value
(Intercept)     1    64 18.555081  0.0001
Treatment       3    12  2.717102  0.0913

Vor- und Nachteile

  • F- und p-Wert für Treatment (Seeigeldichte) sind richtig berechnet.
  • Aber: wir erhalten keine typische ANOVA-Tabelle mit Angabe der Freiheitsgrade und MS sowie der p-Werte der verschachtelten Faktoren.
  • Dafür können wir einige andere Informationen extrahieren …

Variante 3 | summary() Output

summary(mod_lme)
Linear mixed-effects model fit by REML
  Data: sea_urchins 
       AIC      BIC    logLik
  694.1502 708.1346 -341.0751

Random effects:
 Formula: ~1 | Patch_newIDs
        (Intercept) Residual
StdDev:    17.15554 17.28005

Fixed effects:  Algae ~ Treatment 
              Value Std.Error DF   t-value p-value
(Intercept)   39.20  9.407876 64  4.166721  0.0001
Treatment33  -20.20 13.304746 12 -1.518255  0.1548
Treatment66  -17.65 13.304746 12 -1.326594  0.2093
Treatment100 -37.90 13.304746 12 -2.848607  0.0147
 Correlation: 
             (Intr) Trtm33 Trtm66
Treatment33  -0.707              
Treatment66  -0.707  0.500       
Treatment100 -0.707  0.500  0.500

Standardized Within-Group Residuals:
       Min         Q1        Med         Q3        Max 
-1.9807559 -0.3105567 -0.1092864  0.2831185  2.5909912 

Number of Observations: 80
Number of Groups: 16

Variante 3 | Anzeige der Effektgrößen

fixed.effects(mod_lme) # Treatment 0% ist in der intercept versteckt
 (Intercept)  Treatment33  Treatment66 Treatment100 
       39.20       -20.20       -17.65       -37.90 
random.effects(mod_lme)
      (Intercept)
0:1    -4.1565747
0:2    18.9539808
0:3   -30.7586531
0:4    15.9612470
33:1  -13.6335652
33:2  -15.7949840
33:3   15.4624581
33:4   13.9660911
66:1    5.6945074
66:2   12.6775530
66:3  -17.0835222
66:4   -1.2885382
100:1   0.2493945
100:2  -1.0807094
100:3  -0.2493945
100:4   1.0807094

Variante 3 | Varianzkomponenten

Berechnung der prozentualen Varianzkomponenten in der zufälligen Komponente:

VarCorr(mod_lme)
Patch_newIDs = pdLogChol(1) 
            Variance StdDev  
(Intercept) 294.3125 17.15554
Residual    298.6000 17.28005

In der intercept ist der Faktor Patch_newIDs versteckt.

vc <- c(294.3125, 298.6000)
100*vc/sum(vc)
[1] 49.63844 50.36156
  • → Von den zufälligen Effekten entfällt 49.7% der Varianz der Fadenalgenbedeckung auf die unterschiedlichen Patches innerhalb der Dichtestufen.

Variante 3 | Modelldiagnostik

# Zum Nachlesen
?nlme::plot.lme
# Standardisierte Residuen vs. gefittete Werte
plot(mod_lme, resid(., type = "p") ~ fitted(.), abline = 0)

# Box-plots der Residuen vs. Treatment
plot(mod_lme, Treatment ~ resid(.))

# Beobachtete vs. gefittete Werte versus pro Treatment
plot(mod_lme, Algae ~ fitted(.) | Treatment, abline = c(0,1))

Variante 4 - Die ‘Summary Measure
Analysis’

Zum Vergleich
sea_sum <- sea_urchins |> 
  group_by(Treatment, Patch_newIDs) |> 
  summarise(Algae_mean = mean(Algae), n = n())

aov(Algae_mean ~ Treatment, data = sea_sum) |> summary()
            Df Sum Sq Mean Sq F value Pr(>F)  
Treatment    3   2886   961.9   2.717 0.0913 .
Residuals   12   4248   354.0                 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

2-faktorielle Varianzanalyse mit verschachtelten Faktoren
-Beispiel DS2 Fallstudie

Datenaufbereitung

demo <- read.csv("data/Demo_Iris_DatensatzFuerAufgabe2und3.csv", sep =";")
str(demo)
'data.frame':   450 obs. of  15 variables:
 $ Gruppenname : chr  "A-Team" "A-Team" "A-Team" "A-Team" ...
 $ Datum       : chr  "17.4.2023" "17.4.2023" "17.4.2023" "17.4.2023" ...
 $ Uhrzeit     : chr  "14:00" "14:00" "14:00" "14:00" ...
 $ Breitengrad : num  53.6 53.6 53.6 53.6 53.6 ...
 $ Laengengrad : num  9.97 9.97 9.97 9.97 9.97 ...
 $ Standorttyp : chr  "sonnig" "sonnig" "sonnig" "sonnig" ...
 $ Art         : chr  "Iris virginica" "Iris virginica" "Iris virginica" "Iris virginica" ...
 $ Gattung     : chr  "Iris" "Iris" "Iris" "Iris" ...
 $ Familie     : chr  "Iridaceae" "Iridaceae" "Iridaceae" "Iridaceae" ...
 $ Ordnung     : chr  "Asparagales" "Asparagales" "Asparagales" "Asparagales" ...
 $ Pflanzen_ID : int  1 1 1 1 1 1 1 1 1 1 ...
 $ Blueten_ID  : int  1 1 1 2 2 2 3 3 3 4 ...
 $ Kronblatt_ID: int  1 2 3 4 5 6 7 8 9 10 ...
 $ Blattbreite : num  2.15 2.15 2.03 1.77 2 ...
 $ Blattlaenge : num  5.6 5.7 5.6 5.4 5.5 5.5 6 5.8 6 5.6 ...
# ID-Spalten als Faktor definieren
demo$Pflanzen_ID_f <- factor(demo$Pflanzen_ID)
demo$Blueten_ID_f <- factor(demo$Blueten_ID)
demo$Kronblatt_ID_f <- factor(demo$Kronblatt_ID)

# Gruppenname auch als Faktor abspeichern (fuer Modelle)
demo$Gruppenname_f <- factor(demo$Gruppenname,
  levels = c("A-Team", "B Group", "CClub"),
  labels = c("A", "B", "C"))

# Erstellen von einzigartigen IDs und Speicherung der Faktoren als Einzelvektoren
gruppe <- demo$Gruppenname_f
pflanze <- demo$Gruppenname_f:demo$Pflanzen_ID_f
bluete <- demo$Gruppenname_f:demo$Pflanzen_ID_f:demo$Blueten_ID_f

# Eine Datenexploration hat gezeigt, dass die Blattlaenge 
# log-transformiert werden muss
y <- log(demo$Blattlaenge)

Variante 1: aov()

Bei diesem Datensatz dauert Variante 1 sehr (!!!) lange.

mod_aov1_cs <- aov(y ~ gruppe/pflanze/bluete)

# # Das gleiche wie:
# aov(y ~ gruppe + gruppe/pflanze + gruppe/pflanze/bluete)
# aov(y ~ gruppe + gruppe:pflanze + gruppe:pflanze:bluete)
summary(mod_aov1_cs)
                       Df Sum Sq Mean Sq   F value Pr(>F)    
gruppe                  2 141.07   70.53 47018.119 <2e-16 ***
gruppe:pflanze         27   3.45    0.13    85.058 <2e-16 ***
gruppe:pflanze:bluete 120   1.06    0.01     5.881 <2e-16 ***
Residuals             300   0.45    0.00                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Variante 1: aov() | Korrektur

Manuelle Berechnung des F- und p-Werts für Faktor A (gruppe):

correction <- c(
  "F_A korrigiert" = 70.53/0.13,
  "p-Wert korrigiert" = pf(70.53/0.13, df1 = 2, df2 = 27, lower.tail = FALSE)
)
correction
   F_A korrigiert p-Wert korrigiert 
     5.425385e+02      1.587050e-22

Variante 3: nlme::lme()

mod_lme_cs <- nlme::lme(fixed = y ~ gruppe, random = ~ 1 | pflanze/bluete)
anova(mod_lme_cs)
            numDF denDF  F-value p-value
(Intercept)     1   300 4871.267  <.0001
gruppe          2    27  552.779  <.0001

Variante 3: nlme::lme() | Effektgrößen

fixed.effects(mod_lme_cs) # Gruppe A ist in der intercept versteckt
(Intercept)     gruppeB     gruppeC 
  1.6839400  -1.2885207  -0.2374901 
random.effects(mod_lme_cs)
Level: pflanze 
      (Intercept)
A:1   0.026049304
A:2   0.104378797
A:3   0.089879458
A:4  -0.020456987
A:5   0.134588902
A:6  -0.065285951
A:7  -0.040002404
A:8  -0.043275682
A:9  -0.085227928
A:10 -0.100647508
B:1   0.180113993
B:2  -0.085323417
B:3  -0.083100345
B:4  -0.025494836
B:5  -0.057011711
B:6   0.035337550
B:7   0.106376960
B:8   0.024575963
B:9  -0.025535840
B:10 -0.069938317
C:1  -0.116483168
C:2   0.045447014
C:3   0.086482600
C:4  -0.147459911
C:5  -0.058896042
C:6  -0.036848622
C:7   0.055178502
C:8   0.009277929
C:9   0.094217799
C:10  0.069083899

Level: bluete %in% pflanze 
              (Intercept)
A:1/A:1:1    0.0155010746
A:1/A:1:2   -0.0094261918
A:1/A:1:3    0.0584861363
A:1/A:1:4    0.0002688297
A:1/A:1:5   -0.0568013465
A:2/A:2:1   -0.0498614009
A:2/A:2:2    0.0071208528
A:2/A:2:3    0.0341449838
A:2/A:2:4    0.0473656393
A:2/A:2:5   -0.0066001027
A:3/A:3:1    0.0855442808
A:3/A:3:2    0.0280941420
A:3/A:3:3   -0.0683333312
A:3/A:3:4   -0.0277666270
A:3/A:3:5    0.0101627522
A:4/A:4:1   -0.0291775359
A:4/A:4:2   -0.0341148930
A:4/A:4:3    0.0491140579
A:4/A:4:4    0.0589954379
A:4/A:4:5   -0.0511219939
A:5/A:5:1    0.0137078987
A:5/A:5:2    0.0355680547
A:5/A:5:3    0.0004261852
A:5/A:5:4    0.0094231064
A:5/A:5:5   -0.0176443947
A:6/A:6:1    0.0249022444
A:6/A:6:2   -0.0956396202
A:6/A:6:3   -0.0301203959
A:6/A:6:4    0.0456890206
A:6/A:6:5    0.0350473537
A:7/A:7:1   -0.0126235506
A:7/A:7:2    0.0247049991
A:7/A:7:3    0.0401306374
A:7/A:7:4   -0.0572894385
A:7/A:7:5   -0.0072515521
A:8/A:8:1   -0.0315053310
A:8/A:8:2   -0.0260269494
A:8/A:8:3    0.0326913173
A:8/A:8:4    0.0010541610
A:8/A:8:5    0.0104490596
A:9/A:9:1    0.0252306637
A:9/A:9:2   -0.0250983175
A:9/A:9:3    0.0307090453
A:9/A:9:4   -0.0378350797
A:9/A:9:5   -0.0192739080
A:10/A:10:1 -0.0014787929
A:10/A:10:2  0.0430807119
A:10/A:10:3  0.0378110435
A:10/A:10:4 -0.0430931473
A:10/A:10:5 -0.0673397891
B:1/B:1:1    0.0093144799
B:1/B:1:2    0.0692328716
B:1/B:1:3   -0.0214560063
B:1/B:1:4    0.0692328716
B:1/B:1:5   -0.0708123473
B:2/B:2:1   -0.1079738859
B:2/B:2:2    0.0013890781
B:2/B:2:3    0.0218909914
B:2/B:2:4    0.0791514656
B:2/B:2:5   -0.0207546753
B:3/B:3:1   -0.0209578685
B:3/B:3:2    0.0186308696
B:3/B:3:3   -0.0209578685
B:3/B:3:4    0.0186308696
B:3/B:3:5   -0.0209578685
B:4/B:4:1   -0.0482655143
B:4/B:4:2   -0.0086767762
B:4/B:4:3    0.0104100486
B:4/B:4:4    0.0091777560
B:4/B:4:5    0.0294968733
B:5/B:5:1   -0.0426100696
B:5/B:5:2   -0.0016062428
B:5/B:5:3    0.0913632956
B:5/B:5:4   -0.0426100696
B:5/B:5:5   -0.0221081562
B:6/B:6:1   -0.0782512985
B:6/B:6:2   -0.0222231169
B:6/B:6:3   -0.0031362922
B:6/B:6:4    0.0325727721
B:6/B:6:5    0.0819291130
B:7/B:7:1   -0.0096144671
B:7/B:7:2    0.0397418739
B:7/B:7:3    0.0071572878
B:7/B:7:4   -0.0442407541
B:7/B:7:5    0.0397418739
B:8/B:8:1   -0.0502329202
B:8/B:8:2    0.0582760806
B:8/B:8:3    0.0057952614
B:8/B:8:4   -0.0120592707
B:8/B:8:5    0.0057952614
B:9/B:9:1    0.0104440802
B:9/B:9:2    0.0295309049
B:9/B:9:3   -0.0496465713
B:9/B:9:4   -0.0277295692
B:9/B:9:5    0.0295309049
B:10/B:10:1 -0.0523835763
B:10/B:10:2 -0.0318816629
B:10/B:10:3 -0.0318816629
B:10/B:10:4  0.0472958133
B:10/B:10:5  0.0472958133
C:1/C:1:1   -0.0413476957
C:1/C:1:2    0.0660640078
C:1/C:1:3   -0.0181571146
C:1/C:1:4    0.0390524005
C:1/C:1:5   -0.0815121869
C:2/C:2:1    0.0099725693
C:2/C:2:2   -0.0149021073
C:2/C:2:3   -0.0608058907
C:2/C:2:4    0.0517786323
C:2/C:2:5    0.0279637521
C:3/C:3:1   -0.0244951776
C:3/C:3:2   -0.0244951776
C:3/C:3:3    0.0235456522
C:3/C:3:4    0.0518561457
C:3/C:3:5    0.0002428484
C:4/C:4:1    0.0001742116
C:4/C:4:2   -0.0156386196
C:4/C:4:3   -0.0633830158
C:4/C:4:4    0.0717656287
C:4/C:4:5   -0.0383659528
C:5/C:5:1   -0.0364299132
C:5/C:5:2   -0.0364299132
C:5/C:5:3    0.0523177500
C:5/C:5:4    0.0388199887
C:5/C:5:5   -0.0364299132
C:6/C:6:1   -0.0125122732
C:6/C:6:2   -0.0198540083
C:6/C:6:3   -0.0403559217
C:6/C:6:4    0.0275026373
C:6/C:6:5    0.0338626698
C:7/C:7:1   -0.0104016029
C:7/C:7:2    0.0497717806
C:7/C:7:3    0.0139260657
C:7/C:7:4    0.0190947525
C:7/C:7:5   -0.0553847557
C:8/C:8:1    0.0872453527
C:8/C:8:2    0.0022466149
C:8/C:8:3   -0.0307874420
C:8/C:8:4   -0.0372971359
C:8/C:8:5   -0.0185478942
C:9/C:9:1   -0.0368646633
C:9/C:9:2    0.0230755167
C:9/C:9:3    0.0625541178
C:9/C:9:4    0.0230755167
C:9/C:9:5   -0.0428021767
C:10/C:10:1 -0.0285949830
C:10/C:10:2  0.0324066193
C:10/C:10:3  0.0496396485
C:10/C:10:4 -0.0034277107
C:10/C:10:5 -0.0287316337

Variante 3: nlme::lme() | Varianzkomp.

Berechnung der prozentualen Varianzkomponenten in der zufälligen Komponente:

VarCorr(mod_lme_cs)
            Variance     StdDev    
pflanze =   pdLogChol(1)           
(Intercept) 0.007918459  0.08898572
bluete =    pdLogChol(1)           
(Intercept) 0.002440501  0.04940143
Residual    0.001500141  0.03873166
vc <- c( 0.007918460, 0.002440502, 0.001500141) # pflanze, bluete, residuen
100*vc/sum(vc)
[1] 66.77115 20.57914 12.64970
  • → Von den zufälligen Effekten entfällt 67% der Varianz der Blattlängen auf die unterschiedlichen Pflanzen (innerhalb der Gruppen), 20% auf die Blüten (innerhalb der Pflanzen) und 13% auf die einzelnen Kronblätter innerhalb einer Blüte.

Zusammenfassung

  • Bei verschachtelten (hierarchischen) Designs und Pseudoreplikation sind die verschachtelten Faktoren meist zufällige Faktoren.
  • Als Denominator beim F-Quotient des Hauptterms (die Behandlungsstufe meist) gehen die MS des verschachtelten Faktors ein, wenn dieser zufällig ist!
  • Daher ist es wichtig in R, den verschachtelten Faktor eindeutig als zufällig zu definieren.
  • Alle 3 vorgestellten Varianten haben ihre Vor- und Nachteile.
  • Variante 1:
    • ⨁ Wir erhalten die vollständige Tabelle bei einem 2-faktoriellen, verschachtelte Design und können die typischen Diagnostikplots erstellen.
    • ⊖ F- und p-Wert vom Hauptfaktor müssen manuell berechnet werden.
  • Variante 2:
    • ⨁ F- und p-Wert für den Hauptfaktor werden richtig berechnet.
    • ⊖ Wir erhalten keinen F- und p-Wert für unseren verschachtelten Faktor und können keine Modelldiagnostikplots mit plot() erstellen oder Residuen mit residuals() direkt ausgeben.
  • Variante 3:
    • ⨁ F- und p-Wert für den Hauptfaktor werden richtig berechnet und wir können einige Informationen extrahieren wie Effektgrößen und Anteile der Varianzkomponenten.
    • ⊖ Aber: wir erhalten keine typische ANOVA-Tabelle mit Angabe der Freiheitsgrade und MS sowie der p-Werte der verschachtelten Faktoren.

Fragen..??


Total konfus?


Buchkapitel zum Nachlesen

  • The R Book von M.J. Crawley:
    • Kapitel 11.3 Pseudoreplication: Nested designs and split plots
    • Kapitel 19.5 Hierarchical sampling and variance components analysis
  • Experimental Design and Data Analysis for Biologists von G.P. Quinn & M.J. Keough:
    • Kapitel 9.1 Nested (hierarchical) designs

Übungsaufgabe

Übung

  1. Zuhause (VOR der Übung):
    • Durchführung einer 2-faktoriellen, verschachtelten ANOVA für eine Umweltverträglichkeitsstudie (curdies.csv Datensatz).
  2. WÄHREND der Übungsstunde:
    • Durchführung einer 3-faktoriellen, verschachtelten ANOVA auf die Fallstudiendaten aus DS2 (siehe Frage 2 der Fallstudie).

Das R Notebook und der Datensatz für 1. sind im Moodlekurs (Woche 2) zu finden. Das Skript dieser VL ist auch auf Moodle.

Für Aufgabe 2 die Fallstudiendaten aus DS2 mitbringen!

Total gelangweilt?

Dann testen Sie doch Ihr Wissen in folgendem Abschlussquiz…

Abschlussquiz

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de

Creative Commons License
Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.

Kurswebseite: Data Science 3