2-faktorielle Varianzanalyse (gekreuztes Design)

DS3 - Vom experimentellen Design zur
explorativen Datenanalyse & Data Mining

Saskia Otto & Monika Eberhard

Universität Hamburg, IMF

Wintersemester 2025/2026

Lernziele

Am Ende dieser VL- und Übungseinheit werden Sie

das Konzept der gekreuzten 2-faktoriellen Varianzanalyse mit zwei festen unabhängigen Faktoren verstehen und diese auf reale Daten anwenden können.
Haupt- und Wechselwirkungen zwischen den Faktoren identifizieren, interpretieren, und deren Einfluss auf die abhängige Variable beurteilen können.
die Voraussetzung der ANOVA mithilfe von Residuendiagnostiken und auf mögliche Abweichungen hin überprüfen können.
die Ergebnisse der ANOVA, einschließlich der p-Werte und Effektgrößen, korrekt interpretieren und deren Bedeutung für die untersuchte Fragestellung erklären können.
die Ergebnisse durch Effekt- und Interaktionsplots veranschaulichen können.

Theorie

Lineares ANOVA Model

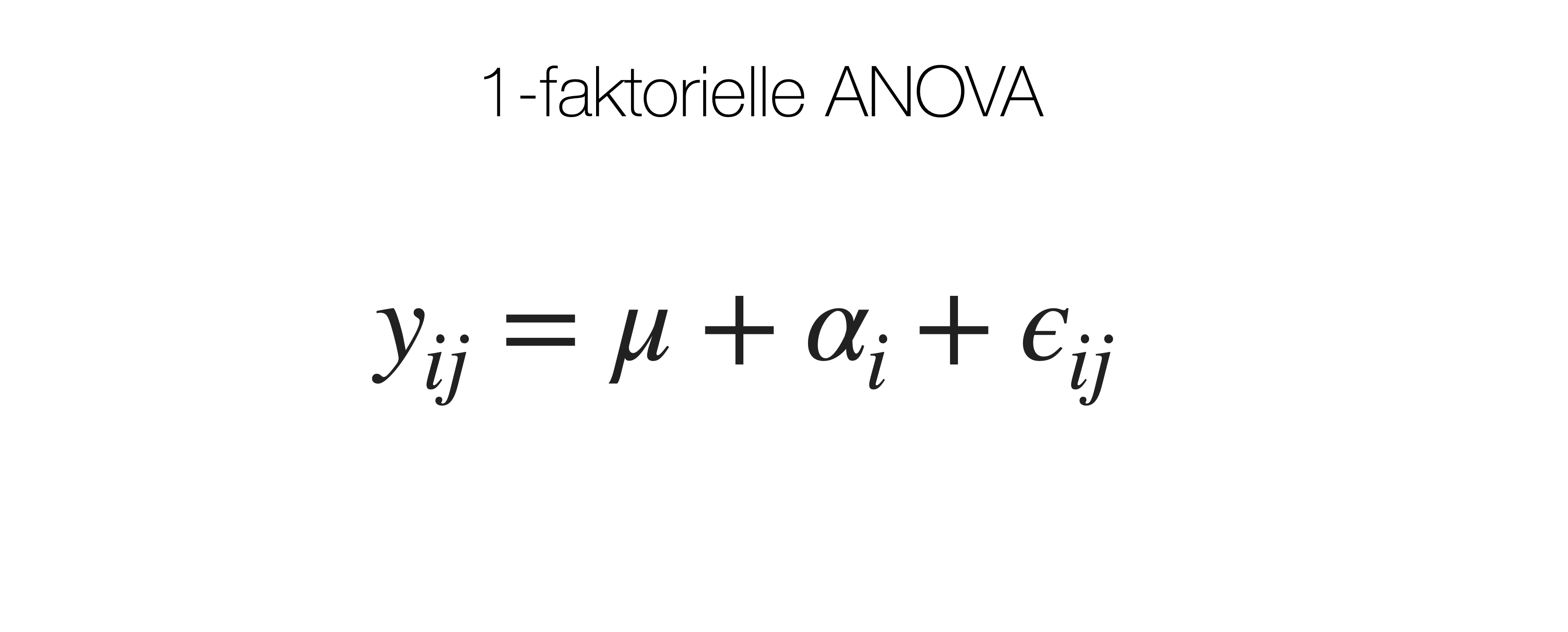
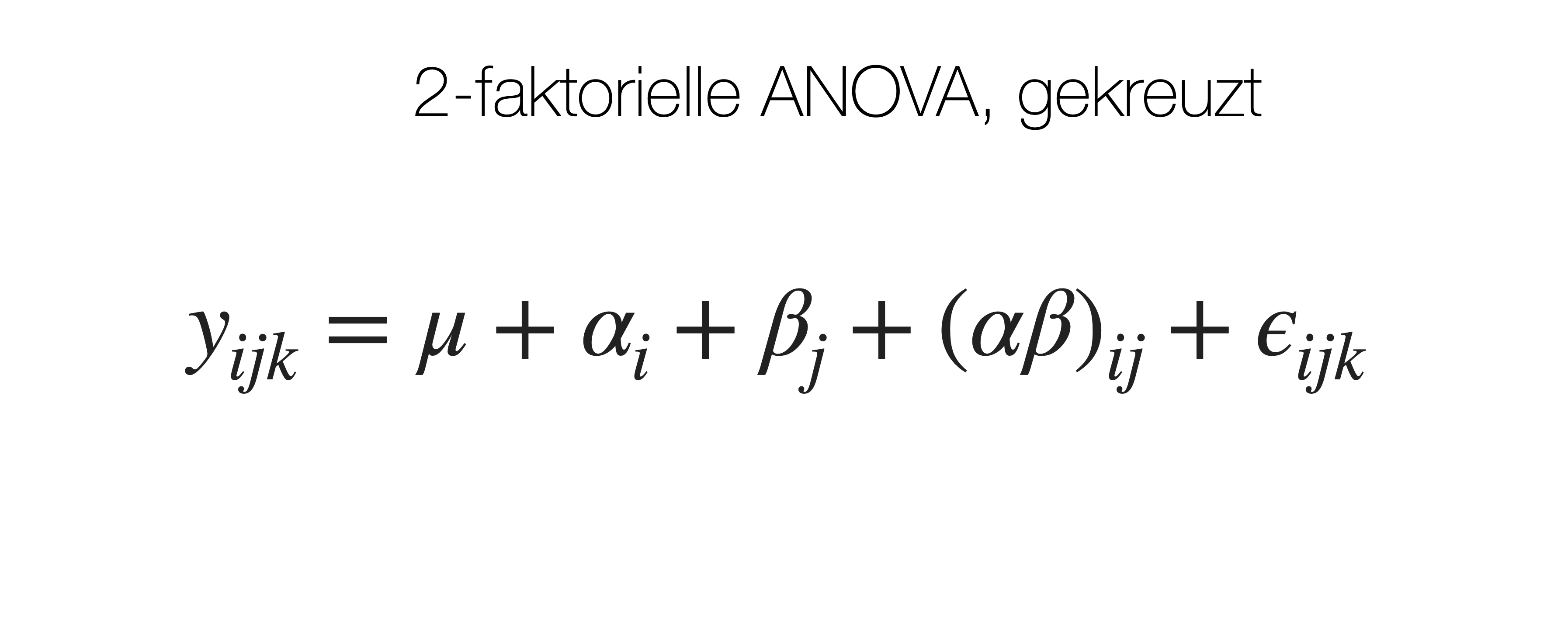
Varianzzerlegung

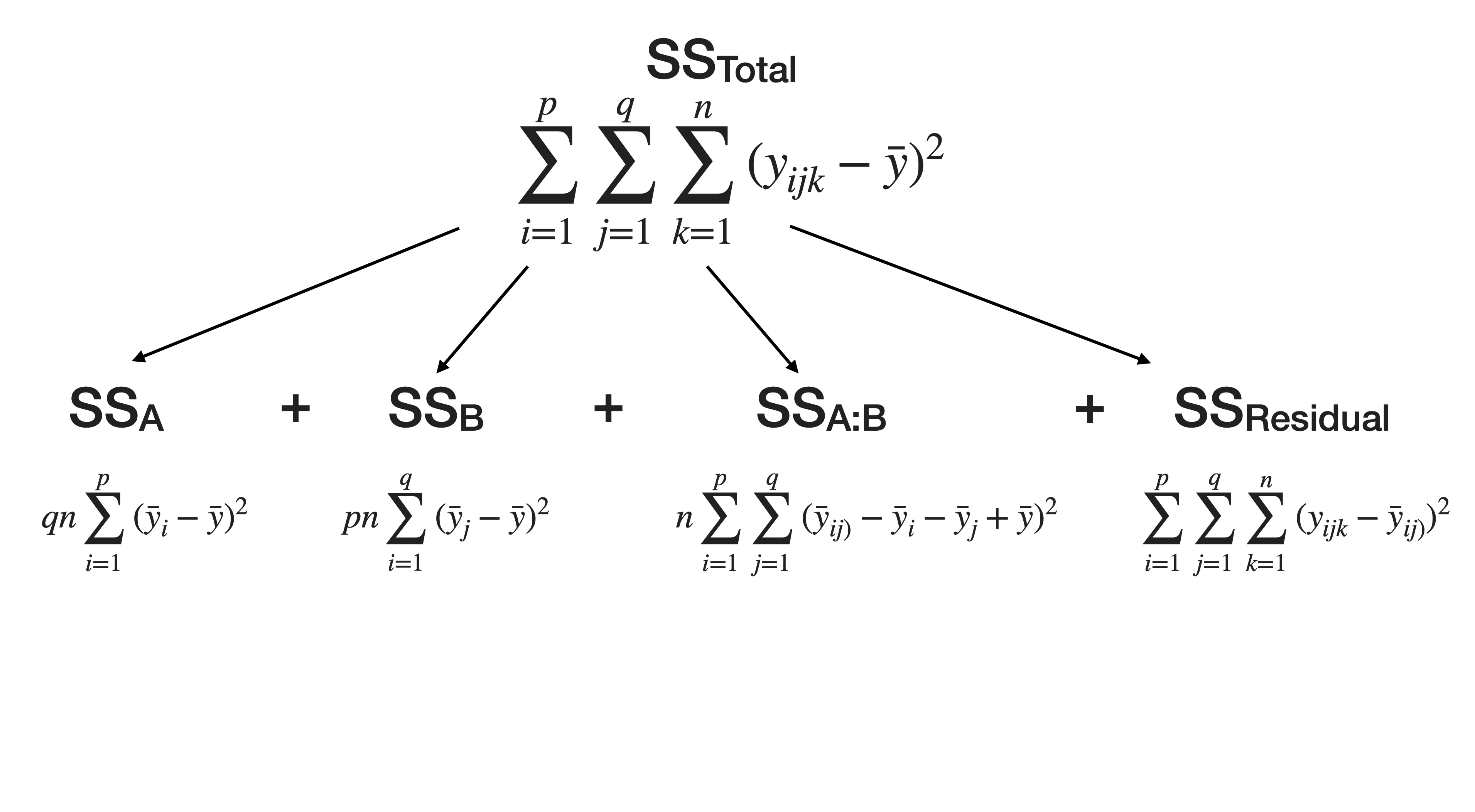
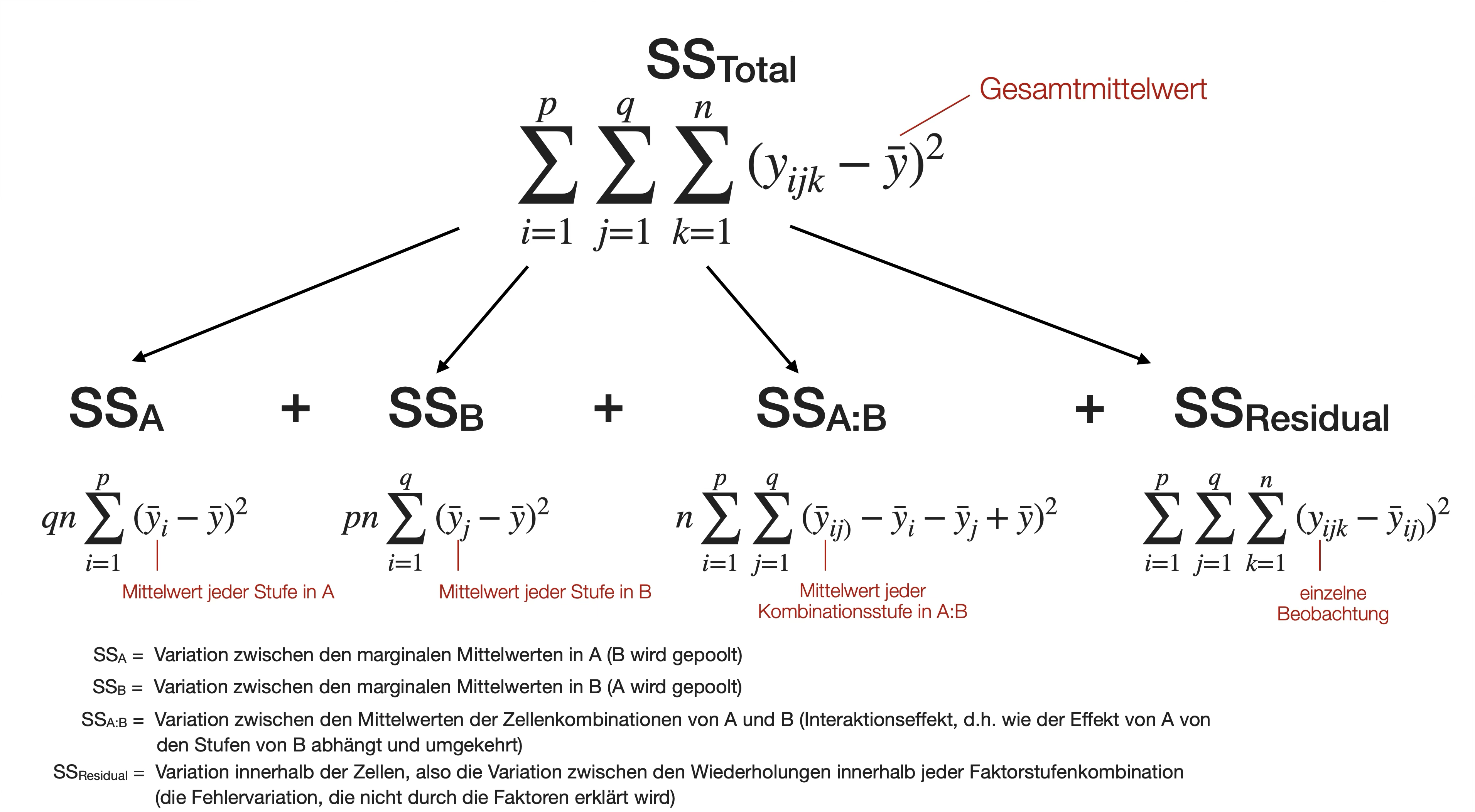
Hypothesen der beiden Haupteffekte

Interaktionen | 1

Wenn die Wirkung eines Faktors von der Höhe eines anderen Faktors abhängt, liegt eine Wechselwirkung vor.
H0 einer 2-Wege-Interaktion: keine Wechselwirkung zwischen Faktor A und Faktor B
- Die Auswirkungen von Faktor A und Faktor B sind unabhängig voneinander.
- Keine gemeinsame Wirkung von A und B.
- \(\alpha\beta_{ij}= 0\) bzw. \(\mu_{ij}-\mu_i-\mu_j+\mu=0\)

Interaktionen | 2

Wenn eine Wechselwirkung vorliegt,

ist es schwierig, den Haupteffekt und die marginalen Mittelwerte zu prüfen.

\(\Rightarrow\) Zuerst H0 der Interaktion testen:

Wenn nicht signifikant, Haupteffekte testen!
Falls signifikant, untersuchen Sie jeden Faktor separat innerhalb der Stufen des anderen Faktors (paarweise Vergleiche!)

Wenn Sie Interaktionsterme einbeziehen wollen,

müssen auch die Hauptterme und alle untergeordneten Terme einbezogen werden!!

Y = A + B + C + AB vs. ~~Y = A + C + AB~~

Interaktionen | Mögliche Effekte

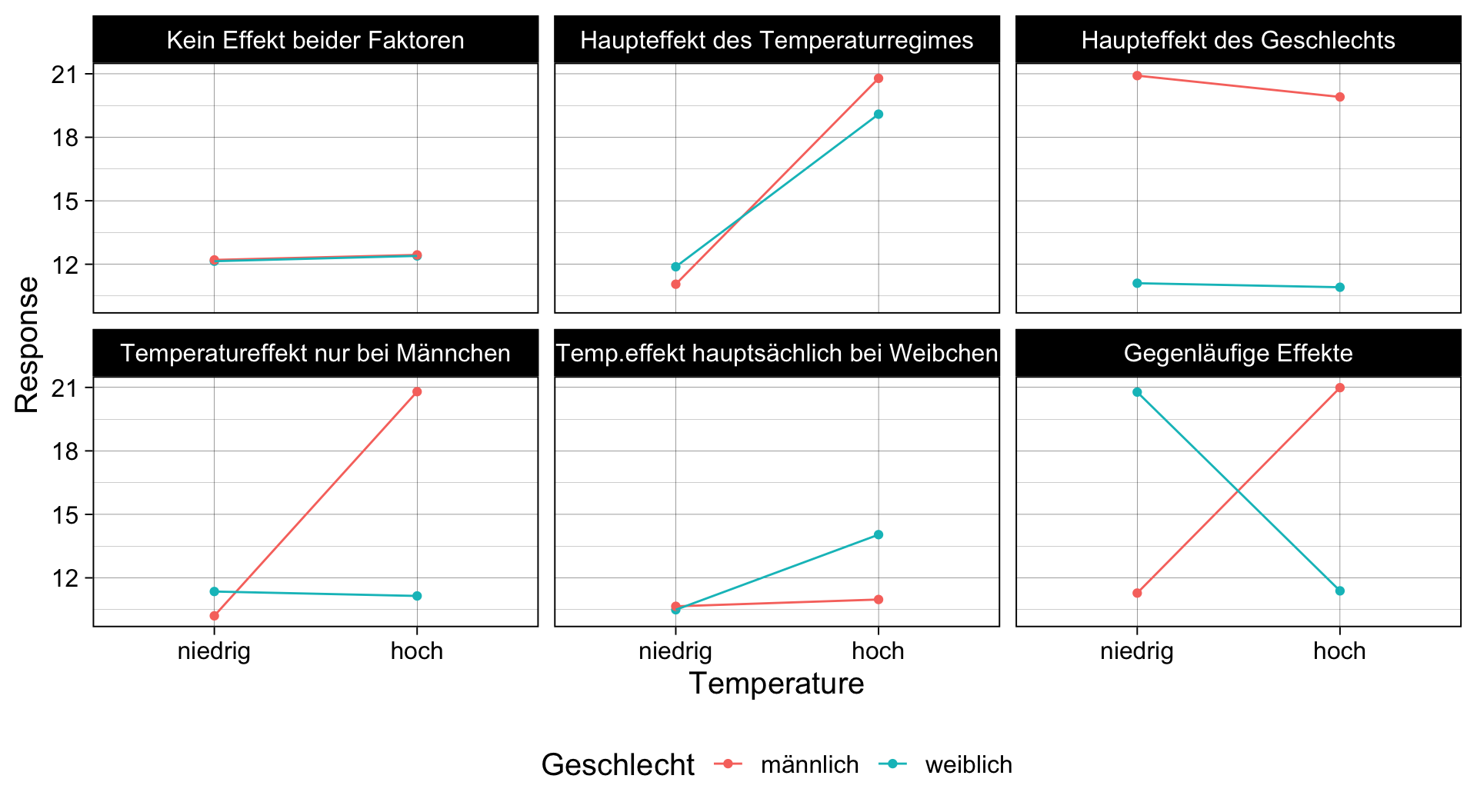
Praxisbeispiel

Napfschnecken Versuch

Quinn (1988) untersuchte die Auswirkungen der Jahreszeit und der Dichte der adulten Tiere auf die Fruchtbarkeit von Napfschnecken (Siphonaria diemenensis).

Antwortvariable Y: mittlere Anzahl der gelegten Eimassen pro Napfschnecke

Beispiel ist aus Kapitel 9.2 in Quinn & Keough (2002): Experimental Design and Data Analysis for Biologists

Die Napfschnecken (ca. 10 mm Schalenlänge) waren in 225 cm2 großen Edelstahlnetzen eingeschlossen, die an der felsigen Plattform befestigt waren. Es gab acht Behandlungskombinationen (vier Dichten zu jeder der beiden Jahreszeiten) und drei Wiederholungen pro Behandlungskombination.
Gekreuztes Design da alle vier Dichten in beiden Jahreszeiten verwendet wurden.
Eine der wichtigsten Fragen, die bei diesem Versuch gestellt wurden, war, ob die Auswirkung der Dichte auf die Anzahl der Eimassen pro Napfschnecke von der Jahreszeit abhängt. Quinn (1988) sagte voraus, dass die Auswirkung der Dichte im Sommer/Herbst, wenn die Algennahrung knapp ist, größer sein würde als im Winter/Frühling, wenn die Algennahrung reichhaltiger ist.

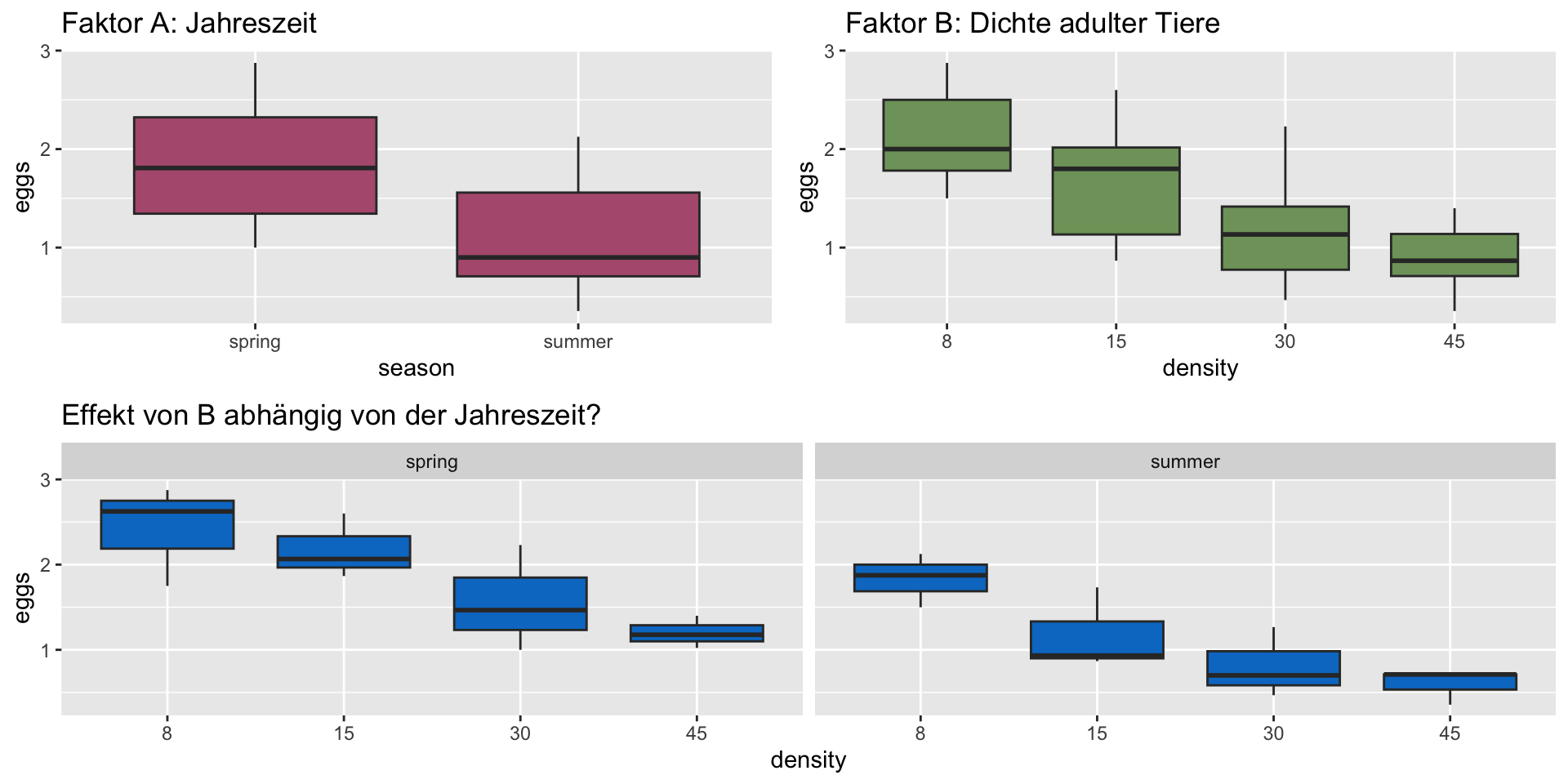
Napfschnecken Versuch | Zellmittelwerte

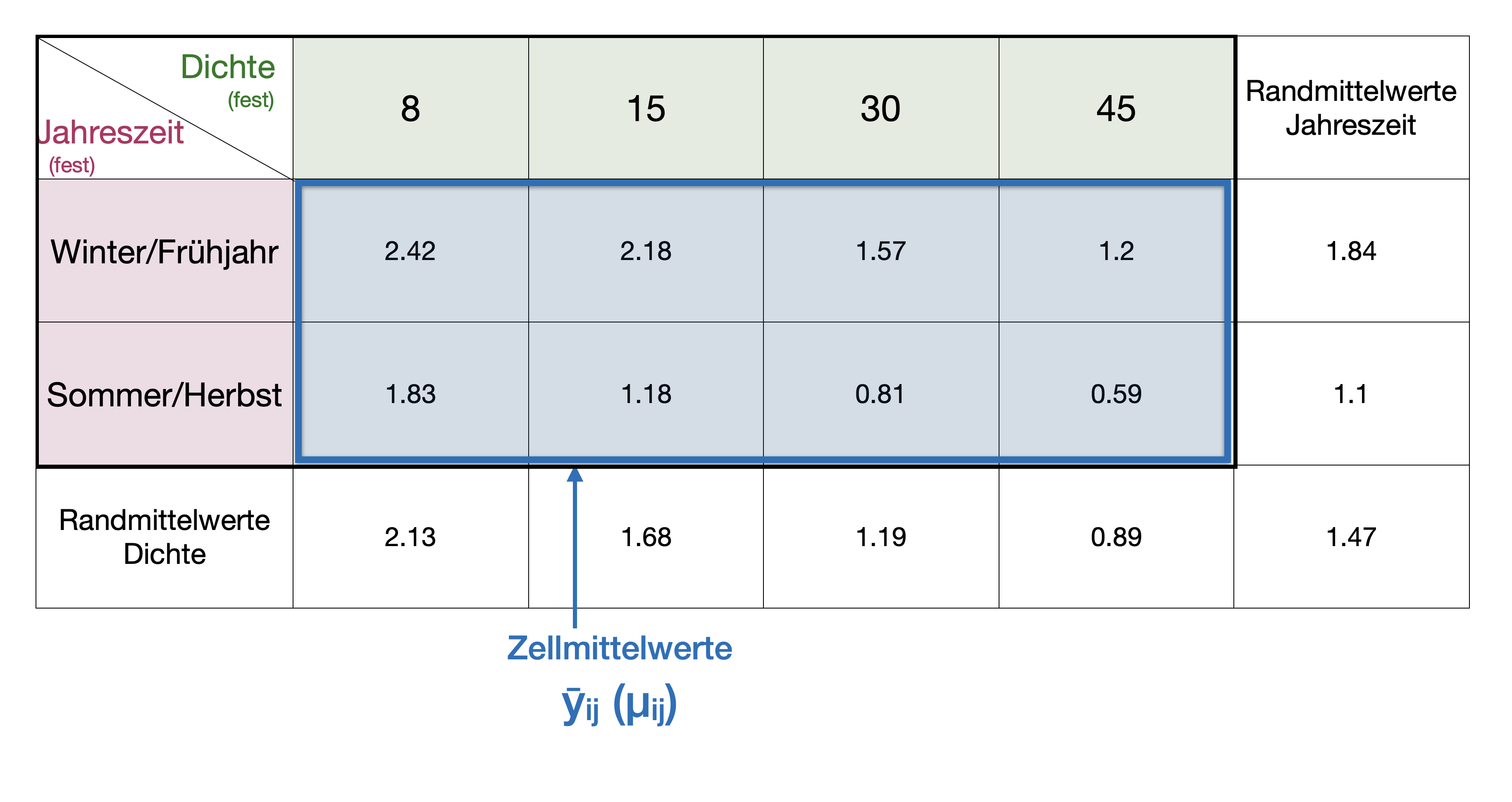
Napfschnecken Versuch | Gesamtmittelwert

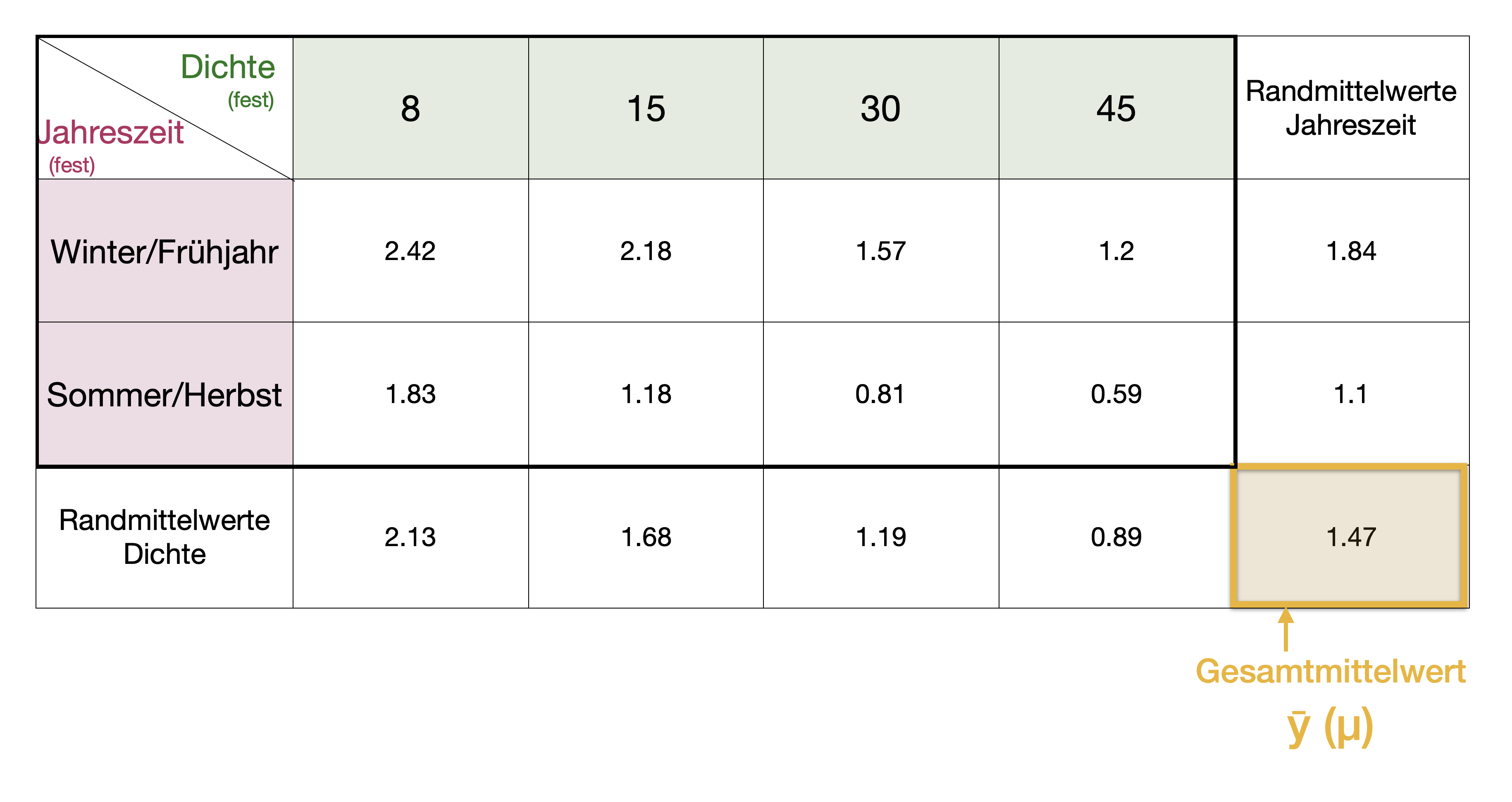
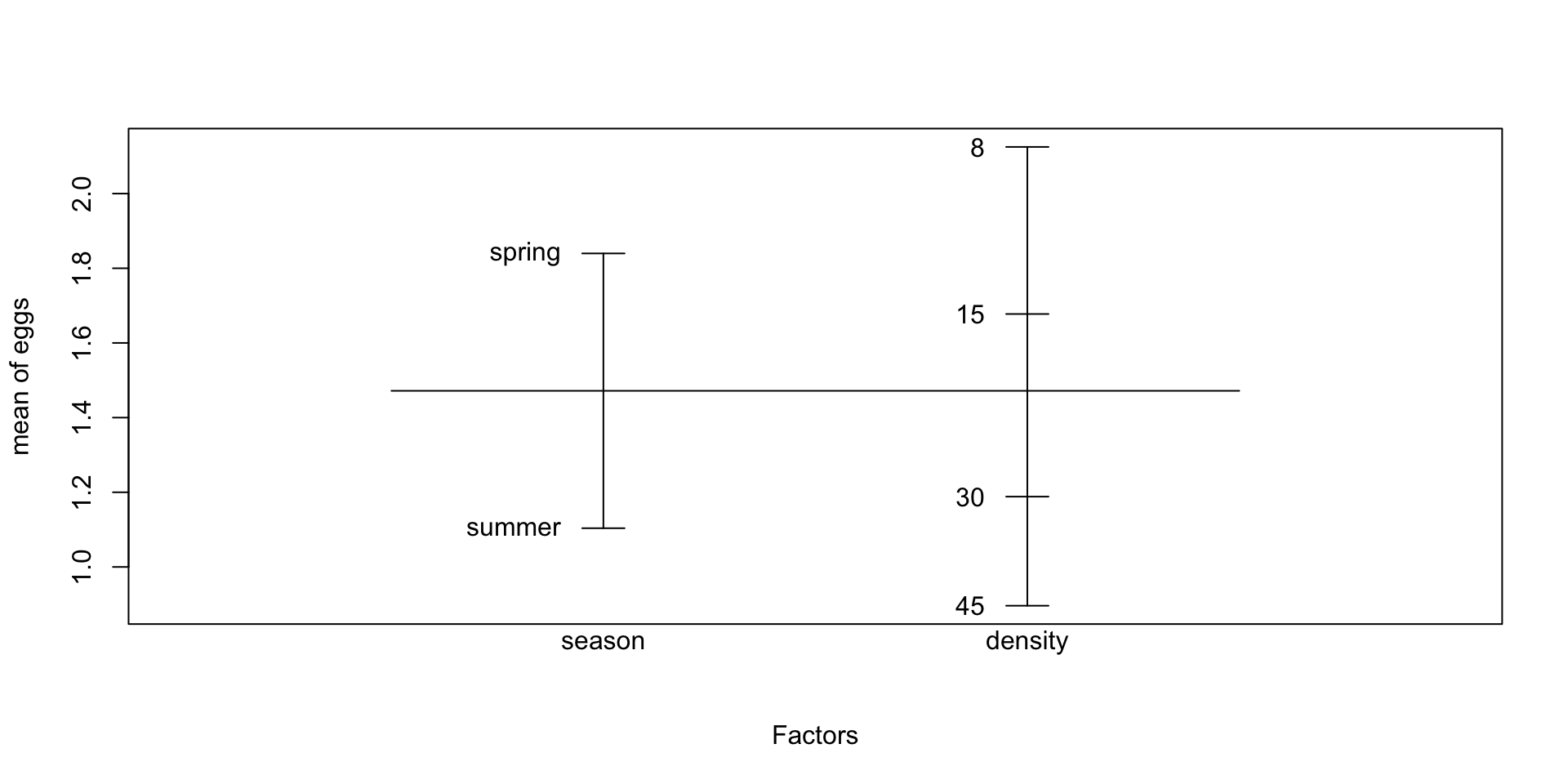
Napfschnecken Versuch | Randmittelwerte

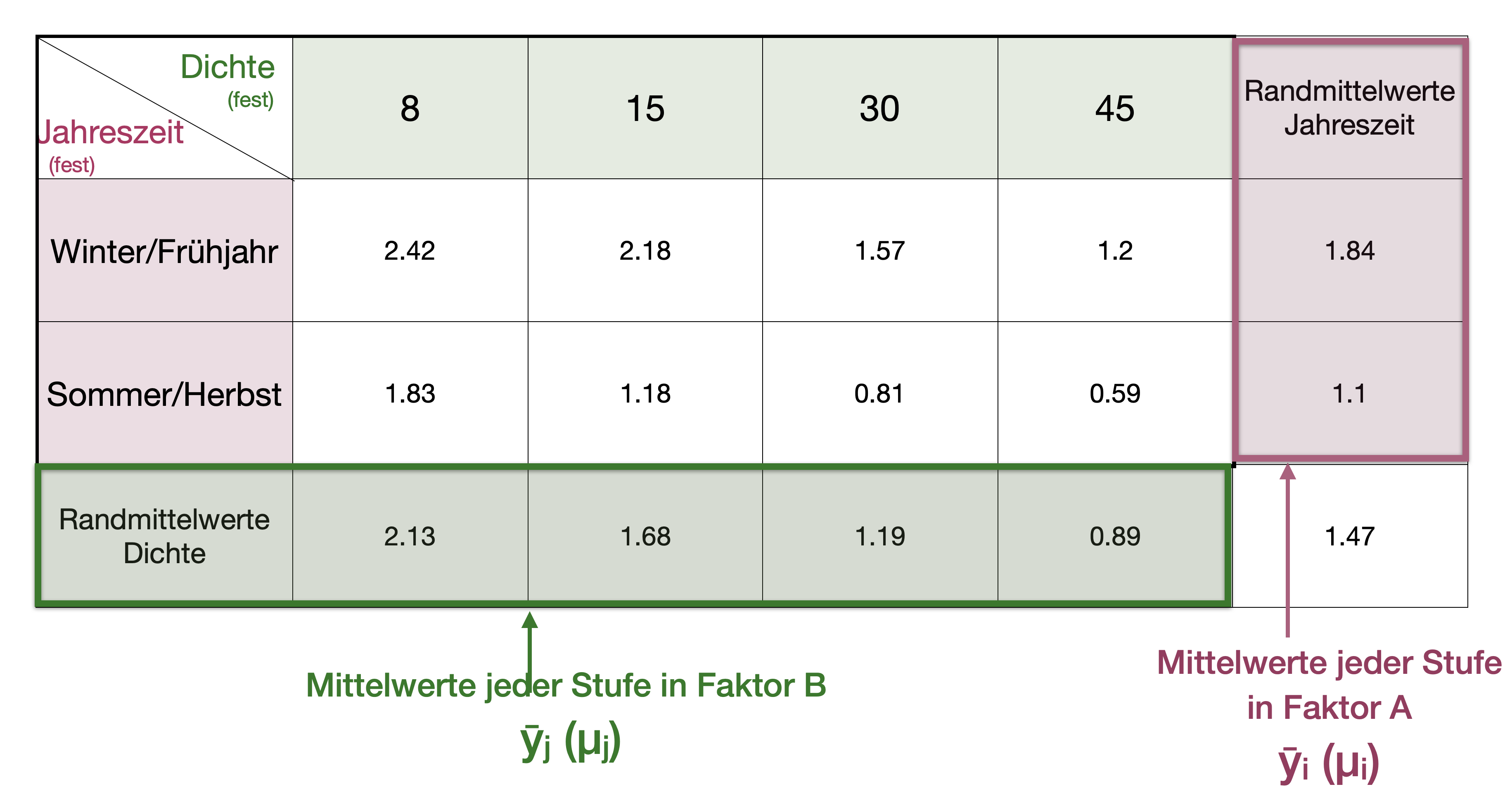
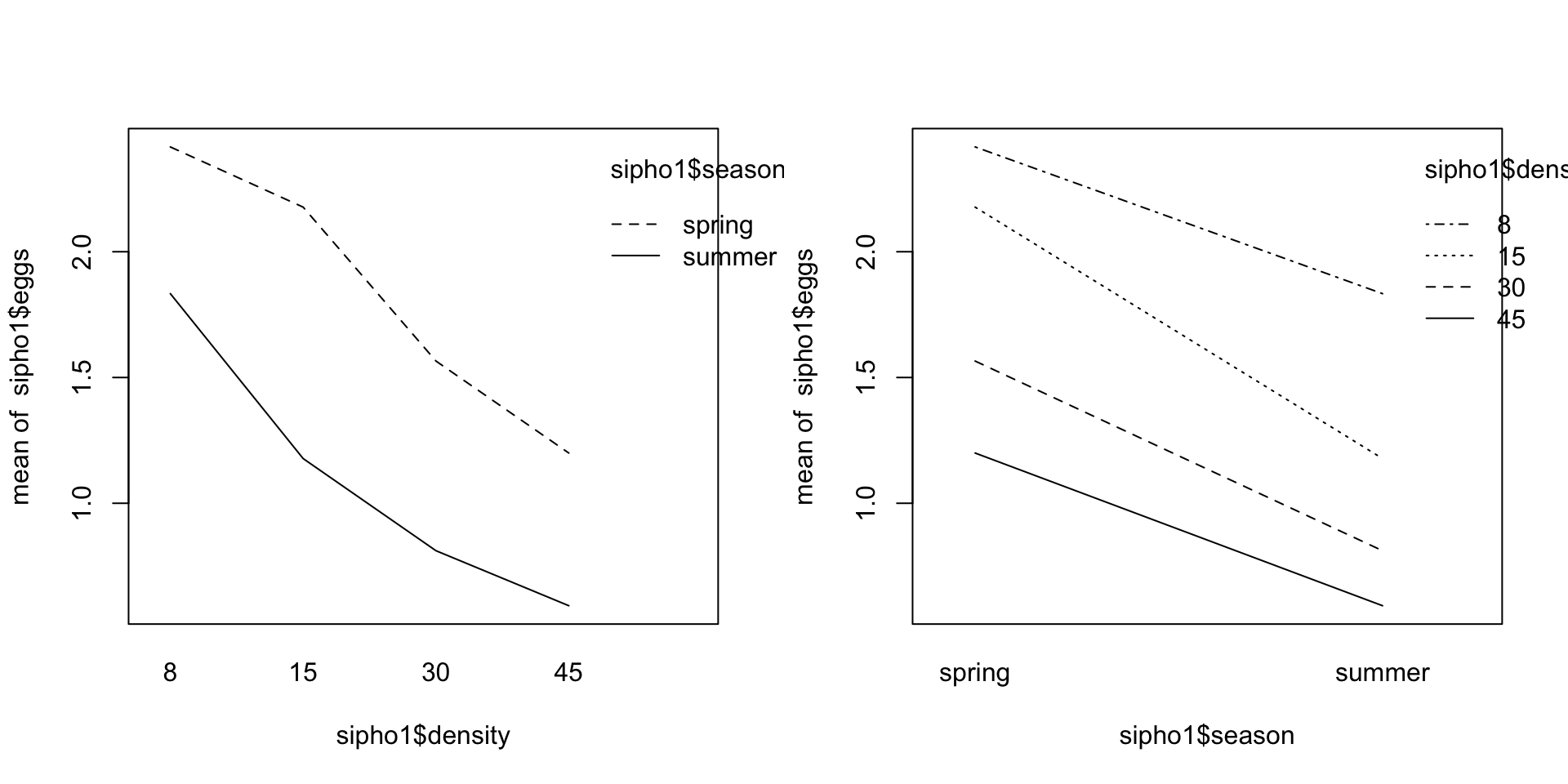
Interaktionen | Grafisch explorieren

Hier ein Beispiel mit einfachen Boxplots:

ANOVA Tabelle bei 2 gekreuzten Faktoren

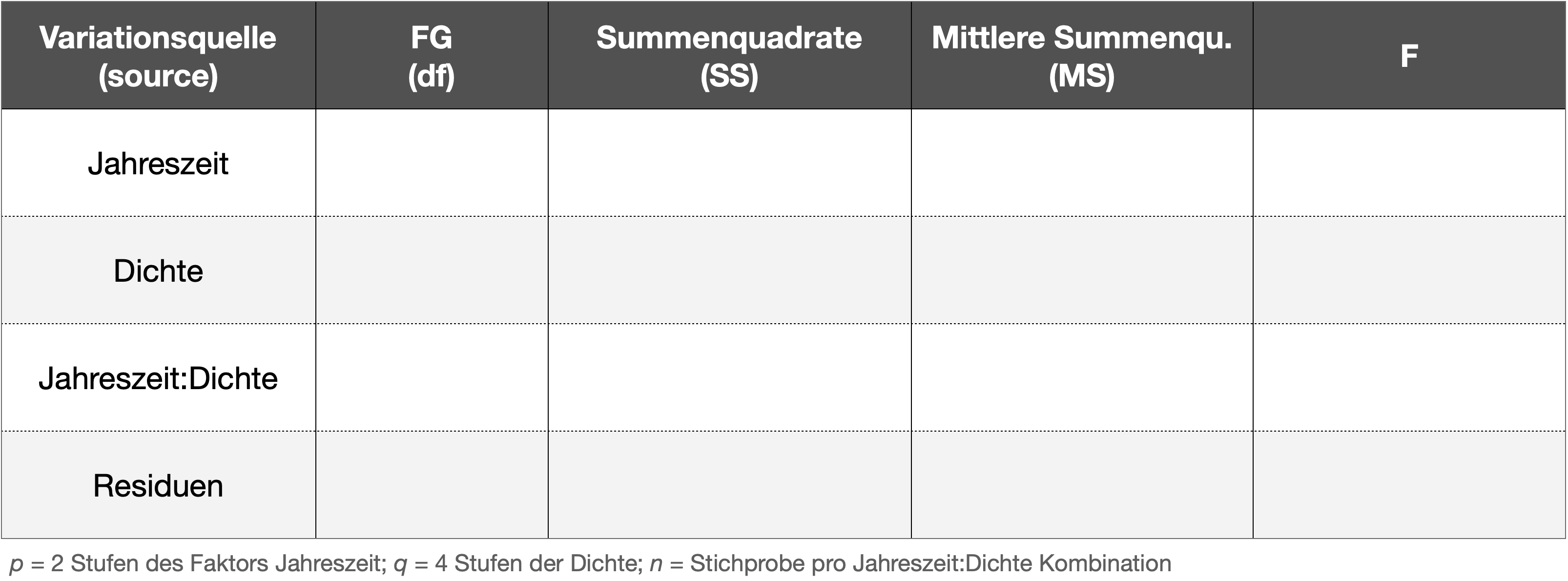
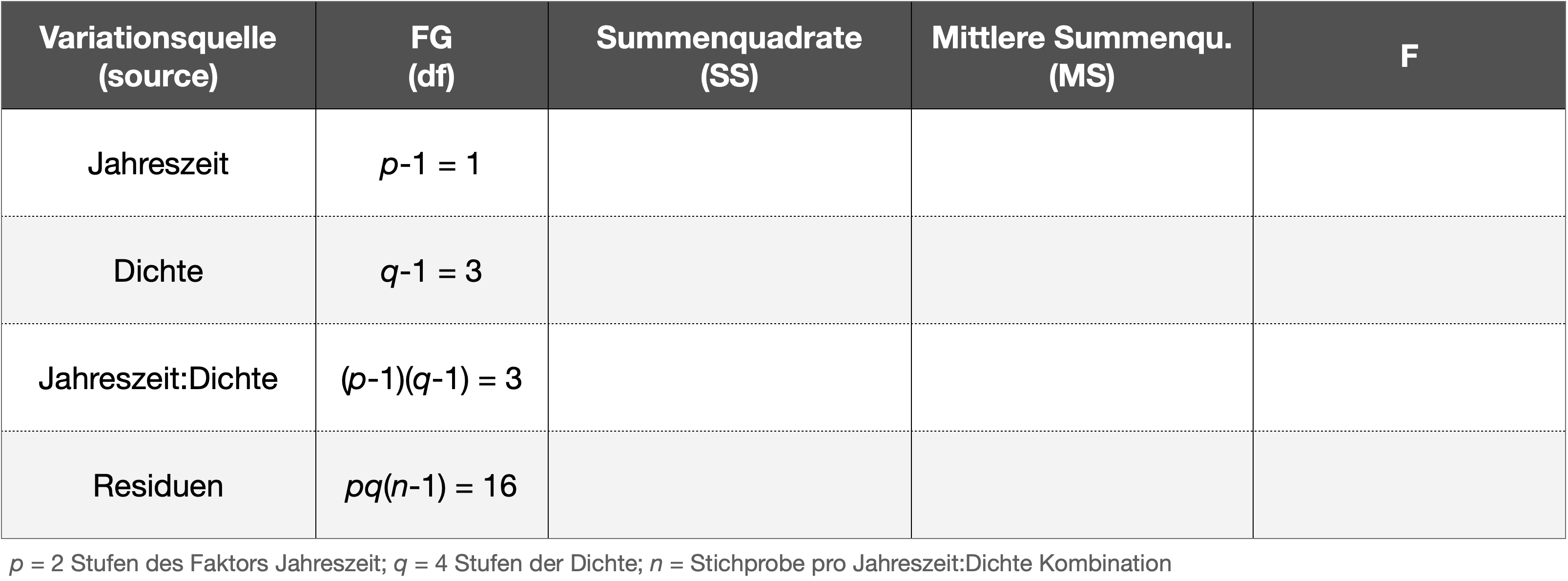
Berechnung der F-Werte

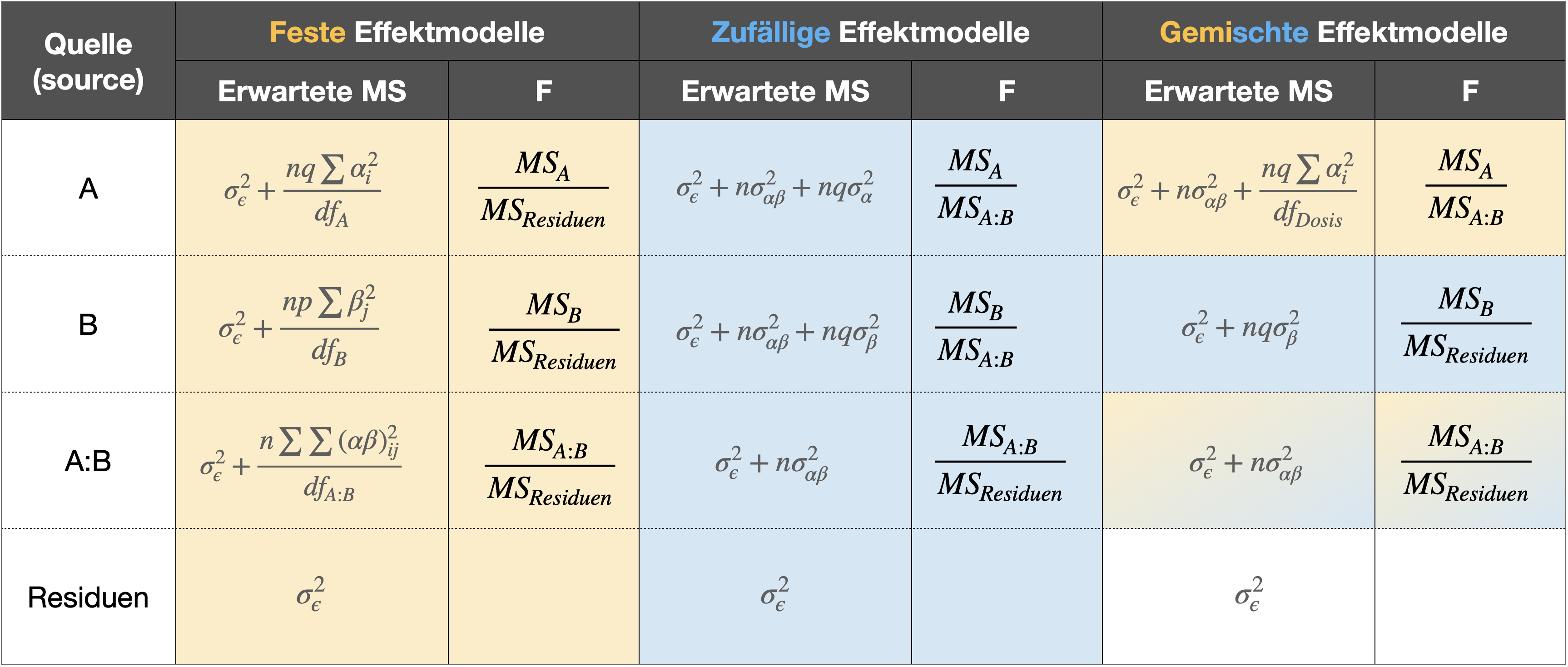
Interpretation der Ergebnisse

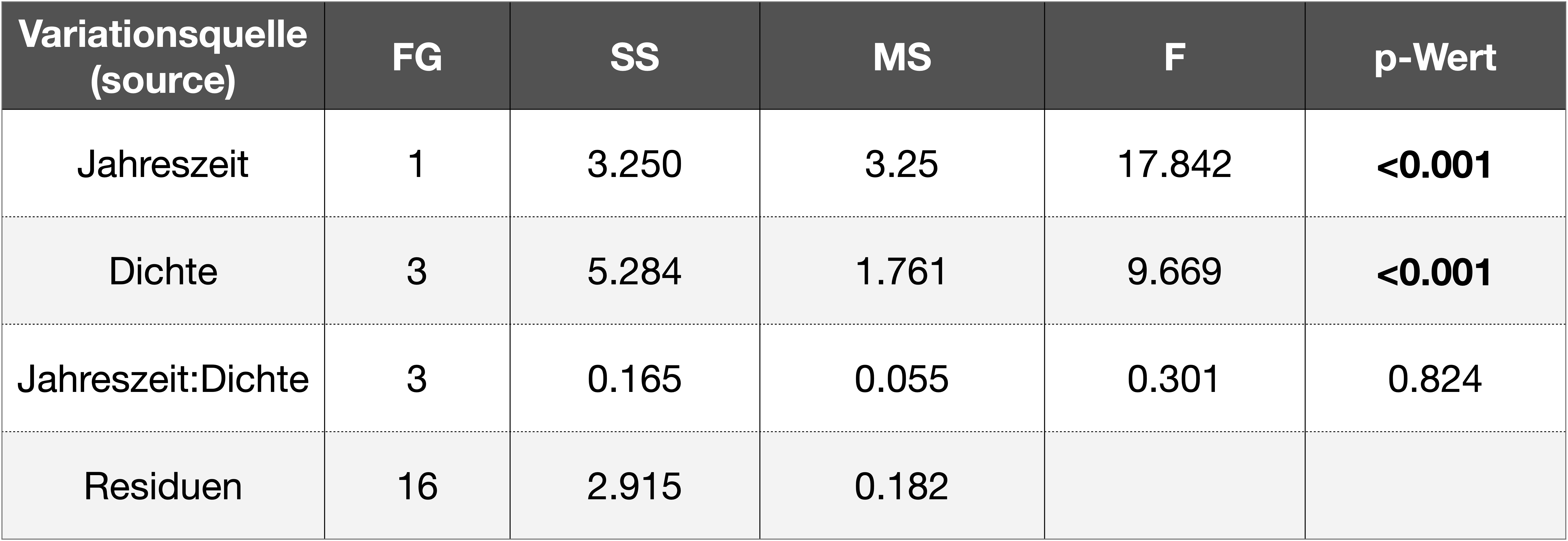
\(\Rightarrow\) Es gibt keine signifikante Interaktion.

\(\Rightarrow\) Es gibt einen sign. Effekt der Jahreszeit und der Dichte auf die Fruchtbarkeit von Napfschnecken (Siphonaria diemenensis).

Durchführung in R

Durchführung in R | 1

ANOVA mit Interaktion

mod1 <- aov(eggs ~ season + density + season:density, data = sipho1)
summary(mod1)

               Df Sum Sq Mean Sq F value   Pr(>F)    
season          1  3.250   3.250  17.842 0.000645 ***
density         3  5.284   1.761   9.669 0.000704 ***
season:density  3  0.165   0.055   0.301 0.823955    
Residuals      16  2.915   0.182                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Kurznotation für Interaktionen

aov(eggs ~ season * density, data = sipho1)

Durchführung in R | 2

ANOVA ohne Interaktion

mod2 <- aov(eggs ~ season + density, data = sipho1)
summary(mod2)

            Df Sum Sq Mean Sq F value   Pr(>F)    
season       1  3.250   3.250   20.05 0.000258 ***
density      3  5.284   1.761   10.87 0.000223 ***
Residuals   19  3.079   0.162                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

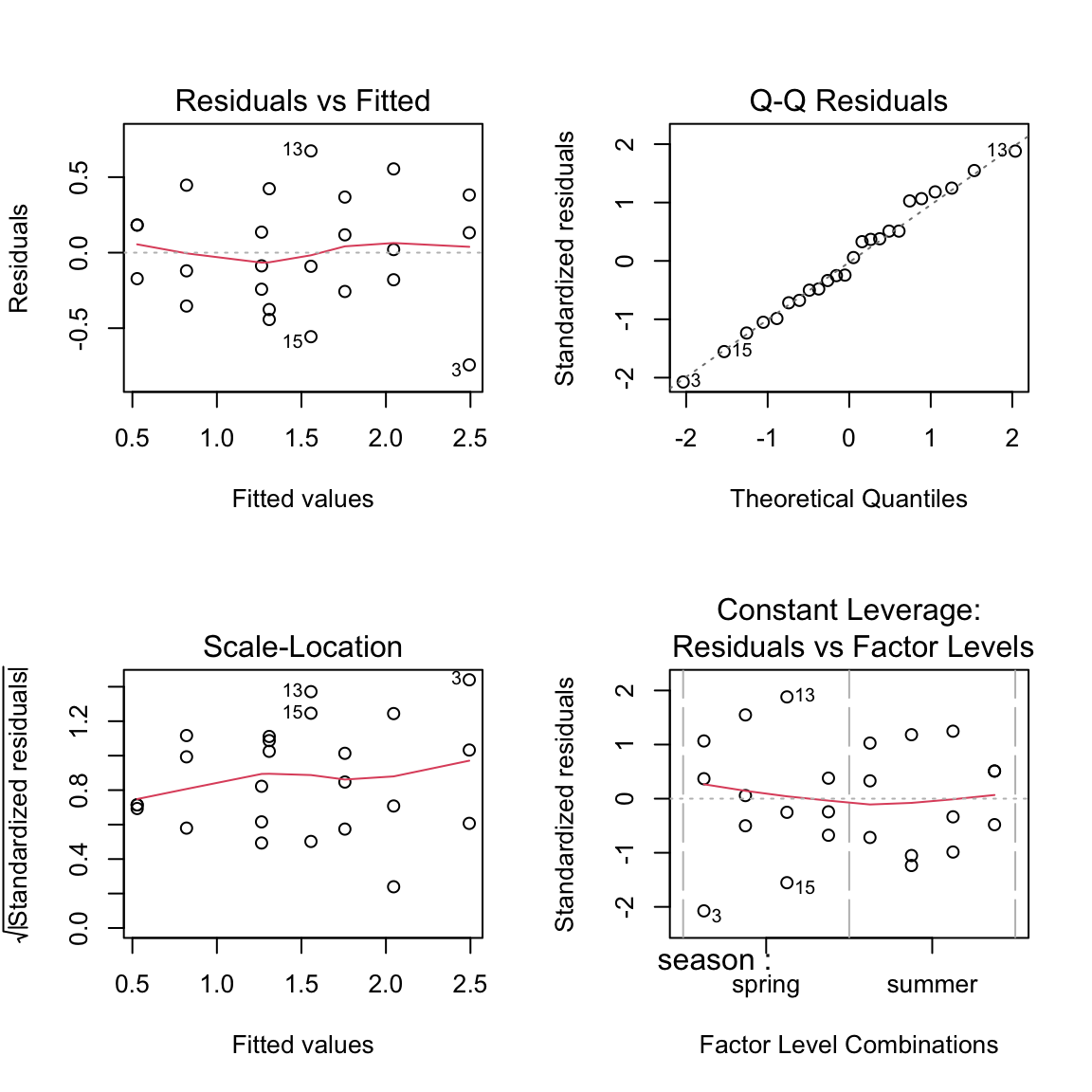
Modelldiagnostik

par(mfrow = c(2,2))
plot(mod2)

Interaktion visualisieren

par(mfrow=c(1,2))
interaction.plot(sipho1$density, sipho1$season, sipho1$eggs)
interaction.plot(sipho1$season, sipho1$density, sipho1$eggs)

Effektgröße

Ein Wert, mit dem Sie feststellen können, wie stark sich Ihre unabhängige Variable (X) auf die abhängige Variable (Y) in einer experimentellen Studie ausgewirkt hat.
Mit anderen Worten, es wird untersucht, wie viel Varianz in Y auf X zurückzuführen ist.
Sie können eine Effektgröße nur berechnen, nachdem Sie einen geeigneten statistischen Test auf Signifikanz durchgeführt haben.

Effektgröße | numerisch

model.tables(mod2, se = T)

Tables of effects

 season 
season
spring summer 
 0.368 -0.368 

 density 
density
      8      15      30      45 
 0.6532  0.2058 -0.2834 -0.5756 

Standard errors of effects
        season density
        0.1162  0.1644
replic.     12       6

Effektgröße | grafisch

plot.design(eggs ~ season + density, data = sipho1)

Your turn …

05:00

Quiz 1 | Formelsyntax

Quiz 2 | R Code

Quiz 3 | Interpretation ANOVA-Tabelle 1

mod <- aov(eggs ~ season * density, data = sipho1)
summary(mod)

                 Df   Sum Sq  Mean Sq  F value    Pr(>F)
season            1     0.25    0.250     0.072    0.792
density           3   247.55   82.517    23.603   <0.001 ***
season:density    3    11.36    3.787     1.083    0.384
Residuals        16    55.94    3.496
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Quiz 4 | Interpretation ANOVA-Tabelle 2

mod <- aov(eggs ~ season * density, data = sipho1)
summary(mod)

                 Df   Sum Sq  Mean Sq  F value    Pr(>F)
season            1   213.47   213.47   103.13   <0.001 ***
density           3   157.96    52.65    25.43   <0.001 ***
season:density    3    45.38    15.13     7.31    0.003 **
Residuals        16    33.07     2.07
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Quiz 5 | Interaktionsplots 1

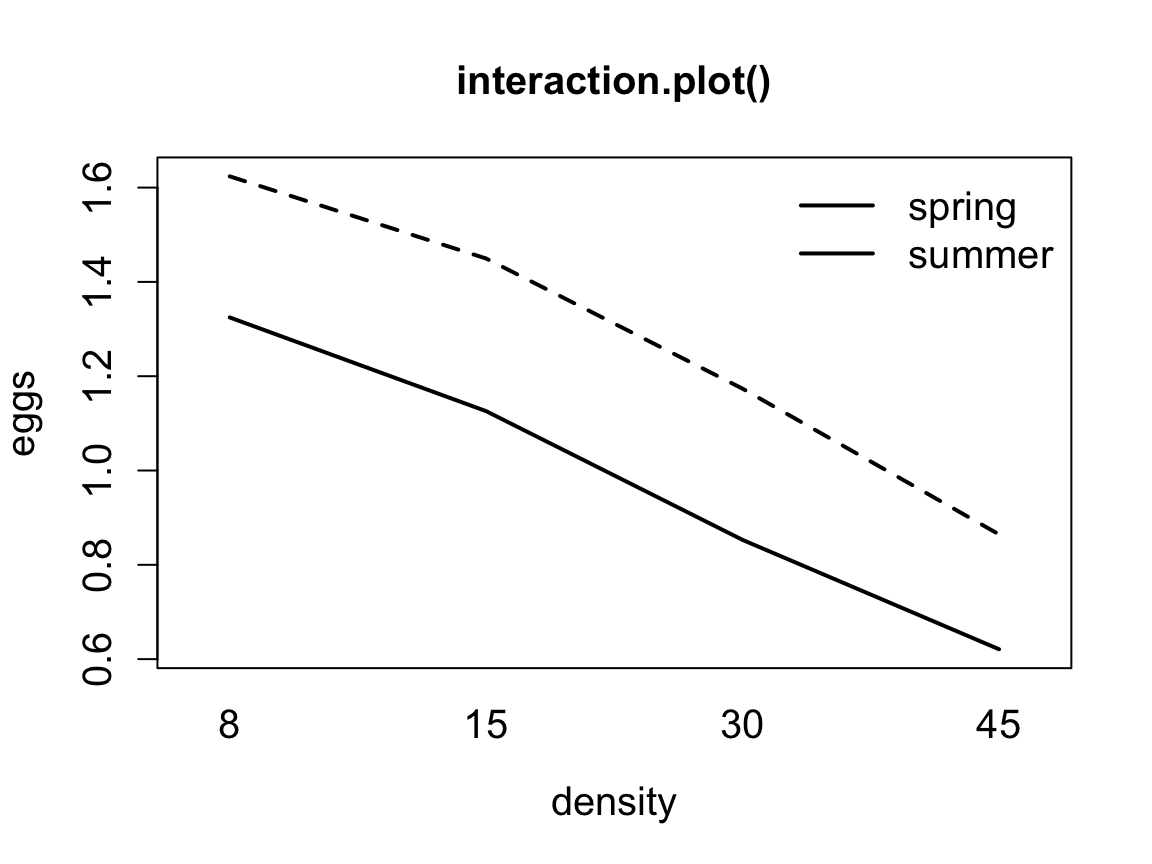
In folgendem Interaktionsplot verlaufen die Linien für spring und summer nahezu parallel.

Gibt es eine Interaktion zwischen den Faktoren season und density?
Was bedeutet das ökologisch?

Quiz 6 | Interaktionsplots 2

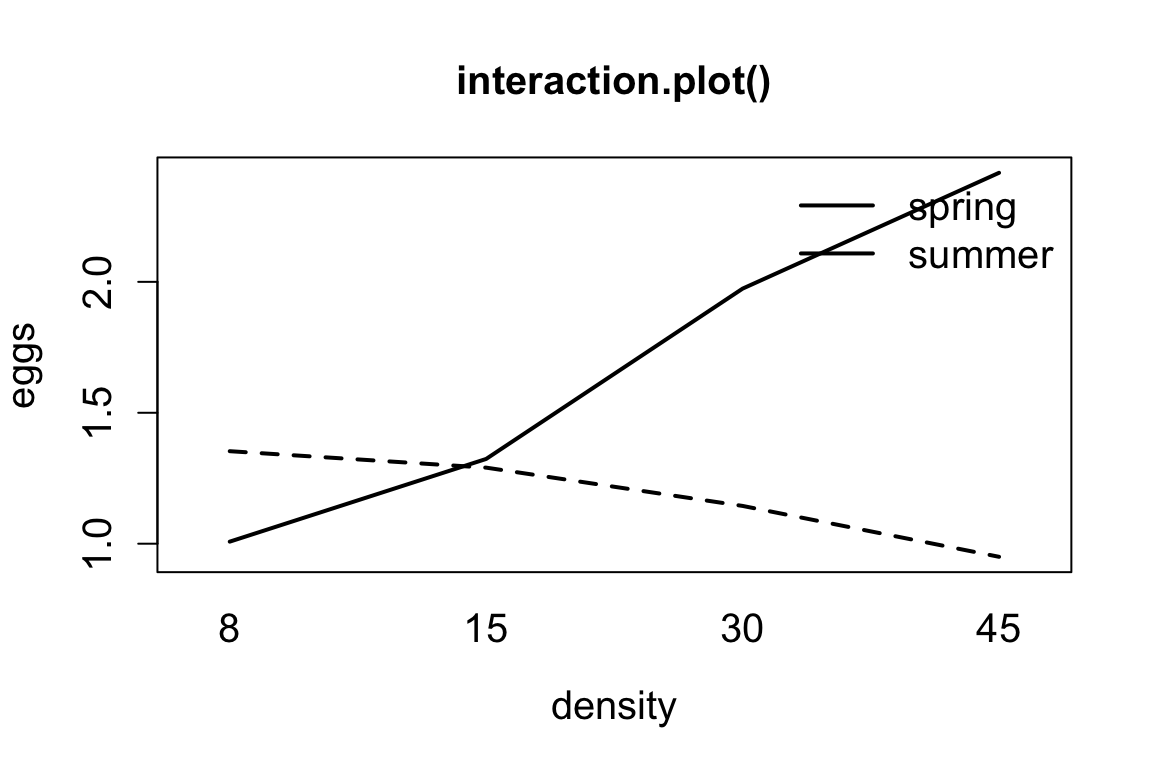
In diesem Interaktionsplot verlaufen die Linien für spring und summer nicht parallel und kreuzen sich sogar.

Gibt es eine Interaktion zwischen den Faktoren season und density?
Was bedeutet das ökologisch?

Übungen

Übungswoche 2

Analyse des Einflusses von Futtermitteln und Zusatzstoffen auf die Gewichtszunahme mittels 2-faktorieller gekreuzter Varianzanalyse

Vorbereitung @home

Datenexploration
Beantworten Sie vor der zweiten Übungsstunde die Fragen zur Datenexploration im Moodle-Quiz.

Fragen..??

Total konfus?

Hilfreiche Buchkapitel zum Nachlesen

Kapitel 11.2 - Factorial experiments in The R Book von M.J. Crawley.
Kapitel 9.2 - Factorial designs in Experimental Design and Data Analysis for Biologists von G.P. Quinn & M.J. Keough

Total gelangweilt?

Dann testen Sie doch Ihr Wissen in folgendem Abschlussquiz…

Abschlussquiz

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de

Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.