Moduleinführung: was ist EDA, DM, ML und SL?

DS3 - Vom experimentellen Design zur
explorativen Datenanalyse & Data Mining

Saskia Otto & Monika Eberhard

Universität Hamburg, IMF

Wintersemester 2025/2026

Modulübersicht

Lernziele des Moduls

Am Ende des Semesters werden Sie …

• grundlegende Kenntnisse zu verschiedenen Methoden des Lernens aus Daten erworben haben,
• ein Verständnis für statistische Modelle entwickelt haben und Methoden wie die Kovarianzanalyse, multiple Regression, lineare gemischte Modelle sowie Resampling-Techniken auf Daten anwenden können,
• die Prinzipien des überwachten und unüberwachten Lernens kennen und bei letzterem zwei grundlegende Methoden der multivariaten Analyse anwenden und interpretieren können.
• die Grundlagen von Open Science und die Anwendung von R Markdown bzw. Quarto zur Dokumentation und Kommunikation wissenschaftlicher Arbeiten beherrschen,
• in der Lage sein, die erlernten Modellierungsverfahren und Analysetechniken auf die Fallstudie aus dem vorherigen Data Science Modul 2 anzuwenden.

Modulstruktur: Theorie & Praxis

Vorlesung

• Wöchentliche VL (75min)
• keine Anwesenheitspflicht
• VL-Aufzeichnungen auf Moodle

Abschließende Klausur (Note)

• 90min, inkl. praktischem Übungsteil
• 1. Termin am 4.2.2026, 10 Uhr (IZS)
• 2. Termin am 16.3.2026, 10 Uhr (IZS)
• ansonsten in jedem folgenden Wintersemester

Übungen

• 7 Übungstage (90min)
• Anwesenheitspflicht!
  • Fehlzeiten max. 15% (1 Übungstag)
• Leistungsnachweis: Moodle-Quizze zu den
  • Vorbereitungsaufgaben (@home)
  • Übungsaufgaben

Das Modul wird als vollständig abgeschlossen betrachtet, sobald beide Komponenten erfolgreich absolviert wurden.

Vorlesungsthemen

VL	Datum	Thema	Übung
1	14.11.2025	Moduleinführung und Wiederholung DS2	→ Übung 1
2	21.11.2025	2-faktorielle, gekreuzte Varianzanalyse (ANOVA)	→ Übung 2
3	28.11.2025	Kovarianzanalyse (ANCOVA)	→ Übung 3
4	05.12.2025	Lineare Gemischte Modelle und verschachtelte ANOVA	→ Übung 4
5	12.12.2025	Multiple lineare Regression
6	19.12.2025	VIDEO: Open Science und R Markdown
-		Weihnachtsferien
7	09.01.2026	Resampling-Techniken	→ Übung 5
8	16.01.2026	Unsupervised Learning 1: Clusteranalyse	→ Übung 6
9	24.01.2026	Unsupervised Learning 2: PCA	→ Übung 7
10	30.01.2026	Wiederholung

Übungsgruppen

Gruppe	Tag & Zeit	Raum	Dozent*in	Termine
A	Mo, 13:30–15:00	IZS, 115	Dr. Kim Rohlfing	17.11./24.11./1.12./8.12./12.1./19.1./26.1.
B	Mo, 13:00–14:30	IPM, E.004	Dr. Dragan Matevski	17.11./24.11./1.12./8.12./12.1./19.1./26.1.
C	Mi, 10:30–12:00	IPM, gr. HS	Dr. Dragan Matevski	19.11./26.11./3.12./10.12./14.1./21.1./28.1.
D	Mi, 10:30–12:00	IZS, 115	Prof. Dr. Kathrin Otte	19.11./26.11./3.12./10.12./14.1./21.1./28.1.
E	Fr, 13:15–14:45	IZS, Kosswig-Saal	Dr. Monika Eberhard	21.11./28.11./5.12./12.12./16.1./23.1./30.1.
F	Fr, 13:15–14:45	IZS, 116	Dr. Kim Rohlfing	21.11./28.11./5.12./12.12./16.1./23.1./30.1.
BMARSYS	Mo, 14:00–15:30	IMF, GES, 107	Dr. Saskia Otto	17.11./24.11./1.12./8.12./12.1./19.1./26.1.

Materialien & Tools

• VL-Folien im HTML-Format
  • https://uham-bio.github.io/bsc-data-science-3/
• Handbuch
  • Allgemeine Modulinformationen
  • Aufgabenstellung Übungen
• R Studio-Projektordner → ZIP-Datei zum Download
  • R Notebooks
  • Daten
• Moodle:
  • VL: PDF-Folien, Aufzeichnungen
  • Quizze begleitend zu den Übungen mit Lösungen
  • Klausur, Klausurvorbereitendes Quiz
  • Kommunikationsplattform
• RStudio Server

Literatur

Deutsch

• Biostatistik - Praktische Einführung in Konzepte und Methoden von F. Bärlocher, 1999, Thieme Verlag, 206 S.
• Parametrische Statistik - Verteilungen, maximum likelihood und GLM in R von C. Dormann, 2017, Springer Spektrum, 363 S.

Englisch

• Experimental Design and Data Analysis for Biologists von G.P. Quinn & M.J. Keough, 2002, Cambridge, UK, 553 S.
• The R Book von M.J. Crawley, 2013, Wiley, 945 S. \rightarrow sehr umfangreiches Buch (fast 1000 Seiten!)
• Mixed Effects Models and Extensions in Ecology with R von A.F. Zuur, E.N. Ieno, N.J. Walker, A.S. Saveliev und G.M. Smith, 2009, Springer Science+Business Media, LLC, NewYork, U.S.A., 574 S. (https://highstat.com)
• An Introduction to Statistical Learning with Applications in R von G. James, D. Witten, T. Hastie und R. Tibshirani, 2013, Springer Science+Business Media, 426 S.
• Numerical Ecology with R von D. Borcard, F. Gillet & P. Legendre, 2011, Springer, 306 S. → für multivariate Statistik

Kommunikationswege

• Stellen Sie so weit wie möglich alle Fragen während der Übungsstunden und nach der Vorlesung.
• Außerhalb dessen läuft die Kommunikation über Moodle:
  • Spezifische Nachrichten bitte direkt an die Übungsgruppenleiter*innen senden (in Moodle).
  • Allgemeine Fragen können im Moodle FAQ Forum gestellt werden, die wir oder auch Sie alle beantworten können.

Sonstiges

• Bitte um Fehlerhinweise und Verbesserungsvorschläge
• Kritischer Umgang mit dem Themengebiet
• Kritik, Fragen, Anmerkungen

Weitere Fragen?

Lernen von Daten

Image by starline on Freepik

Entwicklung der Statistik | 1

• Die Entwicklung der Statistik ist eng gekoppelt an Fragestellungen und Herausforderungen in der Wissenschaft und Industrie.
• In den Anfängen stammten diese Probleme häufig aus landwirtschaftlichen und industriellen Experimenten, waren von relativ geringem Umfang und meist Hypothesen-getrieben
  • → Student’s t-Verteilung und -Test von William Sealey Gosset bei seiner Forschung für die Guinness Brauerei entwickelt.
• In den 1960ern wurde die “Explorative Datenanalyse (EDA)” maßgeblich von dem Statistiker John W. Tukey entwickelt.
• Mit dem Aufkommen von Computern und dem Informationszeitalter sind die statistischen Probleme sowohl vom Umfang als auch von der Komplexität her explodiert.

Entwicklung der Statistik | 2

• Herausforderungen in den Bereichen Datenspeicherung, -organisation und -suche haben zum neuen Gebiet des “Data Mining” geführt.
• Statistische und rechnerische Probleme in Biologie und Medizin haben die “Bioinformatik” hervorgebracht.
• In vielen Bereichen werden riesige Datenmengen generiert, und die Aufgabe des Statistikers besteht darin, aus all diesen Daten einen Sinn zu machen: wichtige Muster und Trends zu extrahieren und zu verstehen, “was die Daten sagen” → Lernen aus Daten.

EDA vs. Data Mining | 1

Die Explorative Datenanalyse (EDA) und Data Mining sind zwei verschiedene, jedoch miteinander verbundene Konzepte im Bereich der Datenanalyse:

Explorative Datenanalyse (EDA)

• ZWECK:
  • Daten erkunden, Muster identifizieren, Hypothesen generieren und einen ersten Einblick in die Daten erhalten.
• METHODEN UND TECHNIKEN:
  • Umfasst die deskriptive Statistik, Datenvisualisierung und einfache statistische Tests.
• STADIUM IM ANALYSEPROZESS:
  • Oft der erste Schritt in der Datenanalyse, um die Daten besser zu verstehen und Hypothesen für weitere Analysen zu generieren.
• ZIELVARIABLEN:
  • Weniger darauf ausgerichtet, vorherzusagen oder spezifische Zielvariablen zu modellieren.

EDA vs. Data Mining | 2

Die Explorative Datenanalyse (EDA) und Data Mining sind zwei verschiedene, jedoch miteinander verbundene Konzepte im Bereich der Datenanalyse:

Data Mining

• ZWECK:
  • Verborgene Muster und Zusammenhänge in großen Datenmengen entdecken, um Vorhersagen zu treffen und Muster zu klassifizieren.
• METHODEN UND TECHNIKEN:
  • Fortgeschrittenere statistische und maschinelle Lernmethoden wie Clusteranalyse, Klassifikation, Regression, Assoziationsregeln.
• STADIUM IM ANALYSEPROZESS:
  • Tritt oft in späteren Stadien der Analyse auf, nachdem die EDA durchgeführt wurde.
• ZIELVARIABLEN:
  • Fokus auf der Modellierung von Zielvariablen.

EDA Demonstration

• Ansatz zur systematischen Erkundung von Daten, um Muster, Trends und Anomalien zu identifizieren.
• Fokus auf Visualisierung: Tukey betonte die Bedeutung von Grafiken und visuellen Darstellungen bei der Datenexploration. Er erkannte, dass Diagramme und Grafiken oft mehr Einblick in die Daten liefern können als rein numerische Analysen.
• Tukey legte Wert darauf, dass die EDA den oft “unordentlichen” Charakter von realen Daten berücksichtigen sollte. Anstatt sich auf formale Modelle zu verlassen, betonte er flexible und anpassungsfähige Ansätze.
• Integration mit anderen Disziplinen: Die EDA hat sich zu einem interdisziplinären Ansatz entwickelt, der nicht nur in der Statistik, sondern auch in Bereichen wie Maschinelles Lernen, Data Science und Datenanalyse weit verbreitet ist.

Lernen aus den Daten

→ Die Wissenschaft des Lernens spielt eine Schlüsselrolle in den Bereichen Statistik, Data Mining und künstliche Intelligenz und überschneidet sich mit Bereichen der Ingenieurwissenschaften und anderen Disziplinen.

Zwei wichtige Ziele bei der Untersuchung biologischer Systeme sind Schlussfolgerungen und Vorhersagen. Bei der Inferenz wird ein mathematisches Modell des Datenerzeugungsprozesses erstellt, um das Verständnis zu formalisieren oder eine Hypothese über das Verhalten des Systems zu testen. Die Vorhersage zielt darauf ab, unbeobachtete Ergebnisse oder zukünftiges Verhalten vorherzusagen, z. B. ob eine Maus mit einem bestimmten Genexpressionsmuster eine Krankheit hat. Die Vorhersage ermöglicht es, die besten Vorgehensweisen zu ermitteln (z. B. die Wahl der Behandlung), ohne dass ein Verständnis der zugrunde liegenden Mechanismen erforderlich ist. In einem typischen Forschungsprojekt können sowohl Schlussfolgerungen als auch Vorhersagen von Nutzen sein - wir wollen wissen, wie biologische Prozesse funktionieren und was als Nächstes passieren wird. Wir möchten zum Beispiel herausfinden, welche biologischen Prozesse mit der Fehlregulierung eines Gens bei einer Krankheit verbunden sind, und feststellen, ob eine Person erkrankt ist, und die beste Therapie vorhersagen.

Viele Methoden der Statistik und des maschinellen Lernens (ML) können im Prinzip sowohl für Vorhersagen als auch für Schlussfolgerungen verwendet werden. Bei den statistischen Methoden liegt der Schwerpunkt jedoch seit langem auf der Inferenz, die durch die Erstellung und Anpassung eines projektspezifischen Wahrscheinlichkeitsmodells erreicht wird. Anhand des Modells lässt sich ein quantitatives Maß für das Vertrauen darauf berechnen, dass eine entdeckte Beziehung einen “wahren” Effekt beschreibt, der mit hoher Wahrscheinlichkeit nicht auf Rauschen zurückzuführen ist. Wenn genügend Daten zur Verfügung stehen, können wir außerdem die Annahmen (z. B. gleiche Varianz) explizit überprüfen und das angegebene Modell bei Bedarf verfeinern.

Im Gegensatz dazu konzentriert sich die ML-Methode auf die Vorhersage, indem sie allgemeine Lernalgorithmen einsetzt, um Muster in den oft umfangreichen und unhandlichen Daten zu finden1,2. ML-Methoden sind besonders hilfreich, wenn man es mit “breiten Daten” zu tun hat, bei denen die Zahl der Eingabevariablen die Zahl der Probanden übersteigt, im Gegensatz zu “langen Daten”, bei denen die Zahl der Probanden größer ist als die der Eingabevariablen. ML macht nur minimale Annahmen über die datenerzeugenden Systeme; sie können selbst dann wirksam sein, wenn die Daten ohne sorgfältig kontrollierten Versuchsplan und in Gegenwart komplizierter nichtlinearer Wechselwirkungen erhoben werden. Trotz überzeugender Vorhersageergebnisse kann das Fehlen eines expliziten Modells jedoch dazu führen, dass ML-Lösungen nur schwer direkt mit dem vorhandenen biologischen Wissen in Verbindung gebracht werden können.

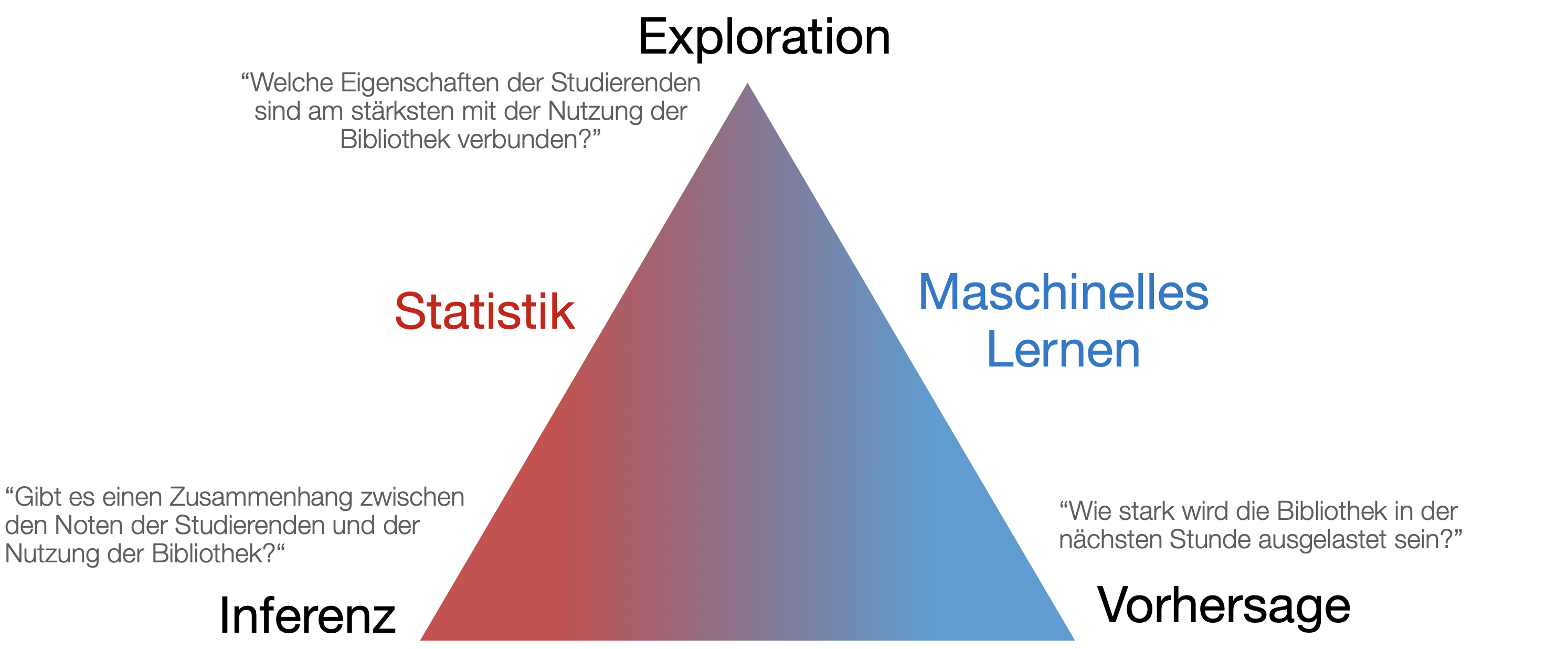
Was macht ML aus?

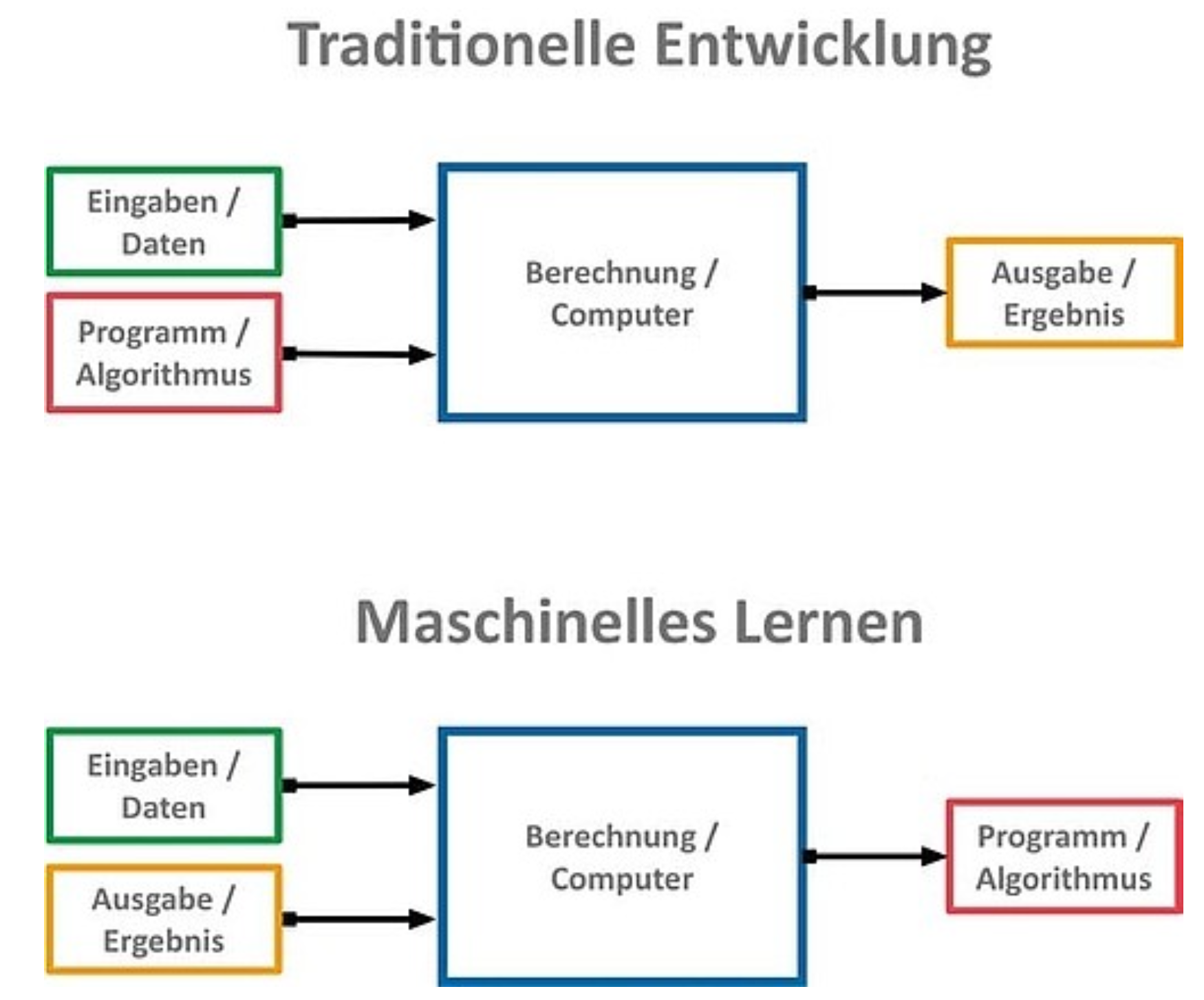
ML | Typisches Anwendungsbeispiel

Bilderkennung

ML | Weitere Anwendungen

• Ermittlung der Risikofaktoren für Prostatakrebs auf der Grundlage klinischer und demografischer Variablen.
• Identifizierung von Mustern in Genexpressionsdaten, um Gene zu identifizieren, die in verschiedenen biologischen Zuständen unterschiedlich reguliert sind → Früherkennung von Krebserkrankungen oder anderen genetisch bedingten Krankheiten.
• Analyse von DNA-Sequenzen, um phylogenetische Beziehungen zwischen verschiedenen Arten zu rekonstruieren.
• Analyse komplexe Metagenomik-Daten zur Erforschung der Rolle von Mikroorganismen in verschiedenen Umgebungen, vom Darm bis zu aquatischen Ökosystemen.
• Analyse von ökologische Daten und Entwicklung von Modellen, die uns helfen, die Verbreitung von Arten vorherzusagen, Ökosysteme zu schützen oder invasive Arten zu kontrollieren.

Was ist statistisches Lernen?

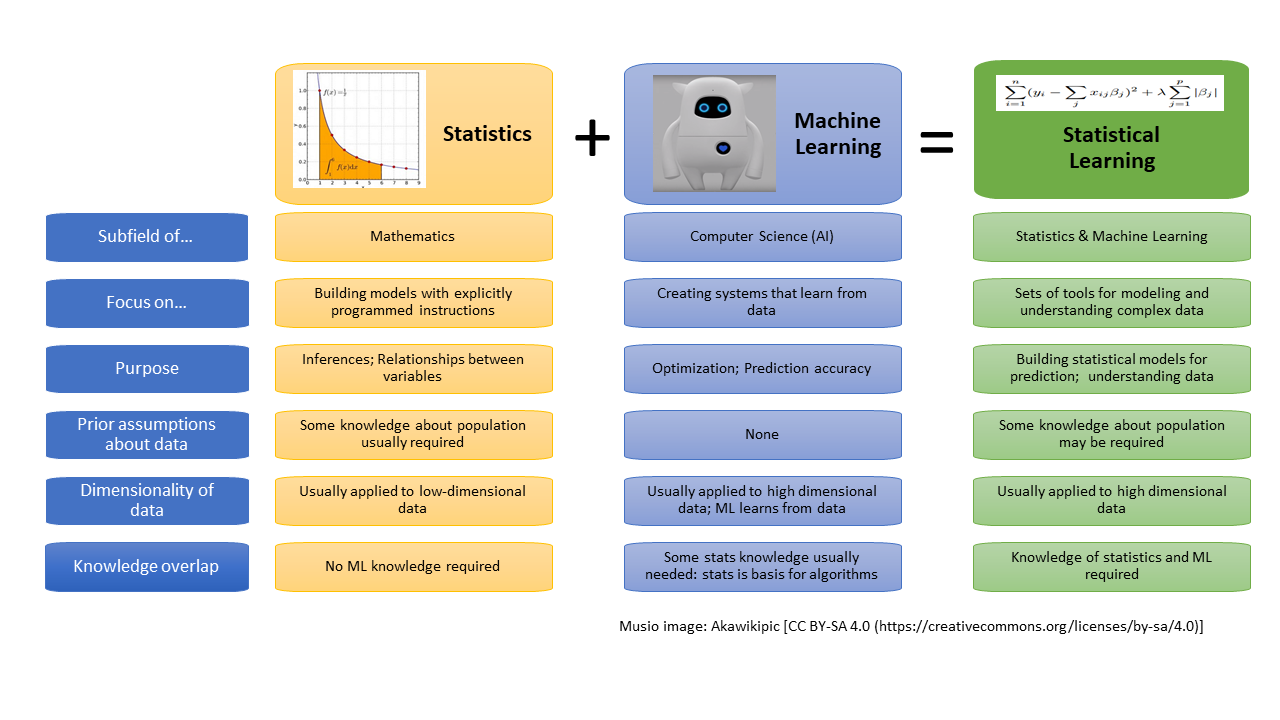
• Maschinelles Lernen ist ein Teilgebiet der Künstlichen Intelligenz.
• Statistisches Lernen entstand als Teilgebiet der Statistik.
• Es gibt viele Überschneidungen - beide Bereiche konzentrieren sich auf überwachte und nicht überwachte Probleme:
  • Beim ML liegt der Schwerpunkt stärker auf groß angelegten Anwendungen und der Vorhersagegenauigkeit.
  • Beim SL liegt der Schwerpunkt auf Modellen und deren Interpretierbarkeit sowie auf Präzision und Unsicherheit.
• Unterscheidung verschwimmt immer mehr.

Beide Methoden (ML und SL) sind datenabhängig. Statistisches Lernen beruht jedoch auf regelbasierter Programmierung; es ist in Form von Beziehungen zwischen Variablen formalisiert, während maschinelles Lernen aus Daten ohne explizit programmierte Anweisungen lernt. Statistisches Lernen basiert auf einem kleineren Datensatz mit wenigen Attributen, im Gegensatz zum maschinellen Lernen, das aus Milliarden von Beobachtungen und Attributen lernen kann. Statistisches Lernen basiert auf Annahmen wie Normalität, keine Multikollinearität, Homoskedastizität usw., während maschinelles Lernen nicht so sehr von Annahmen abhängig ist und diese in den meisten Fällen ignoriert. Beim statistischen Lernen geht es vor allem um Schlussfolgerungen, die meisten Ideen werden aus der Stichprobe, der Grundgesamtheit und der Hypothese abgeleitet, im Gegensatz zum maschinellen Lernen, bei dem Vorhersagen, überwachtes Lernen, unüberwachtes Lernen und halbüberwachtes Lernen im Vordergrund stehen. Statistisches Lernen ist rechenintensiv, basiert auf dem Koeffizientenschätzer und erfordert ein gutes Verständnis Ihrer Daten. Beim maschinellen Lernen hingegen werden durch Iterationen Muster in Ihrem Datensatz identifiziert, was einen weitaus geringeren menschlichen Aufwand erfordert. Auch wenn die meisten argumentieren werden, dass maschinelles Lernen besser ist, stimme ich ihnen bis zu einem gewissen Grad zu. Im Gegenteil, mit der Anwendung des statistischen Lernens machen Sie sich besser mit Ihren Daten vertraut, was Ihnen hilft, das nötige Vertrauen in Ihre Modellierung aufzubauen.

‘Supervised’ vs. ‘Unsupervised’ Learning

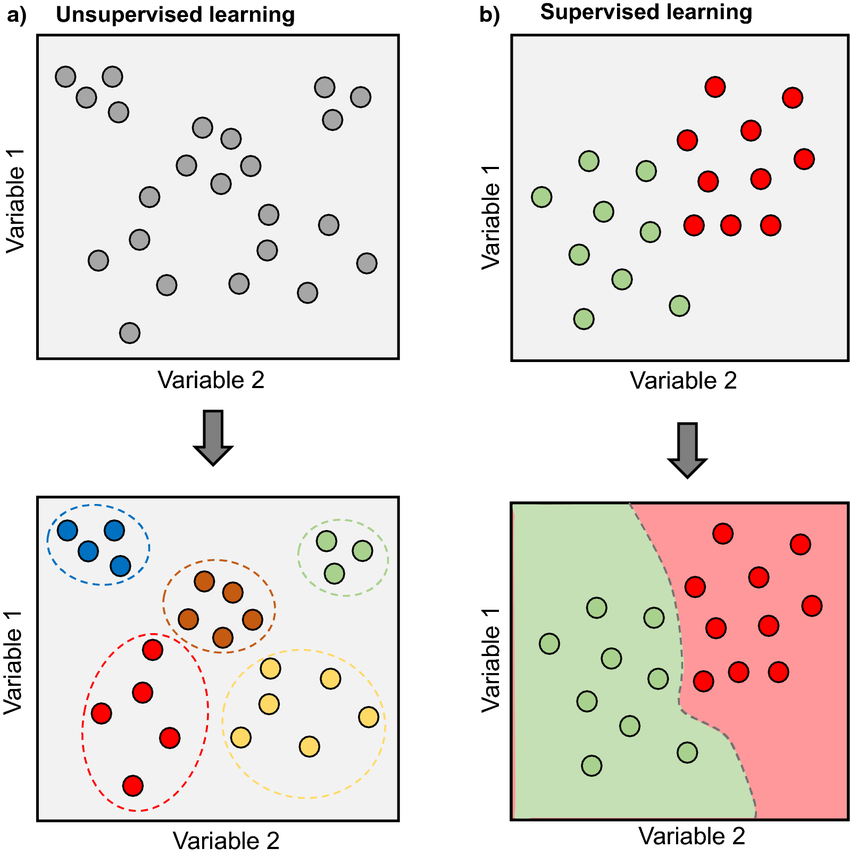
Bildquelle: Morimoto & Ponton (2021): Virtual reality in biology: could we become virtual naturalists?

Im überwachten Lernen (supervised learning) werden Modelle auf Grundlage von Input-Output-Paaren trainiert, während im unüberwachten Lernen (unsupervised learning) Modelle Muster in den Eingabedaten ohne explizite Ausgabeinformationen entdecken.

Supervised Learning

• Ein statistisches Modell wird zur Vorhersage oder Schätzung einer Antwortvariable (Zielvariable, Output) auf der Grundlage einer oder mehrerer unabhängiger Variablen (Inputs) erstellt.
• Dabei ‘lernt’ der Algorithmus aus einem Trainingsdatensatz, indem er iterativ Vorhersagen zu den Daten macht und die vorhergesagte mit der richtigen Antwort vergleicht.
• Ziel ist es, dass der Algorithmus eine Zuordnung von Eingangsvariablen zu Ausgangsvariablen erlernt, die es ihm ermöglicht, Vorhersagen oder Klassifizierungen für neue, nicht gekennzeichnete Daten zu treffen → Optimierung ist das Ziel

Supervised Learning | Häufige Verwendung

• Klassifizierung verschiedener Dateitypen wie Bilder, Dokumente oder geschriebene Wörter.
• Vorhersage zukünftiger Trends und Ergebnisse durch Lernen von Mustern in Trainingsdaten mittels Regression

Supervised Learning | Vorgehensweise

• Die Daten erhalten (viele!!!)
• Daten aufbereiten
• Daten in Trainings- und Validierungs-/Testdaten aufteilen
• Einen Modelltyp auswählen
• Sich für eine Verlustfunktion entscheiden
• Optimierungsalgorithmus (und Lernrate) festlegen [ML]
• Anpassen (“Trainieren”) des Modells
• Bewertung der Modellleistung anhand von Validierungs-/Testdaten (und anderen unabhängigen Datensätzen)

Was ist Optimimierung?

• Wir versuchen, die Parameter eines Modells zu bestimmen (z. B. lineare/logistische Regression).
• Wir berechnen die Verlustfunktion für die Parameter unseres Modells zur Bewertung wie gut das Modell die Zielgröße der Trainingsdaten vorhersagt.
• Der Verlust ist die Abweichung zwischen Vorhersage und Beobachtung
• Typische Verlustfunktion, die für die Modellgenauigkeit herangezogen wird: mittlerer quadratischer Vorhersagefehler bzw. ‘Mean Squared Error’. MSE = \frac{1}{n}\sum_{i=1}^{n}(Y_i - \hat{Y}_i)^2

Ein paar Kompromisse…

• Vorhersagegenauigkeit versus Interpretierbarkeit.
  • Lineare Modelle sind leicht interpretierbar, andere wie ‘thin-plate splines’ sind es nicht.
• Gute Anpassung versus Überanpassung oder Unteranpassung.
  • Wie wissen wir, wann die Anpassung genau richtig ist?
• Sparsamkeit versus Blackbox.
  • Oft bevorzugen wir ein einfacheres Modell mit weniger Variablen gegenüber einem Blackbox-Prädiktor, der alle einschließt.

Flexibilität vs. Interpretierbarkeit

Im Allgemeinen sinkt die Interpretierbarkeit je flexibler eine Methode ist.

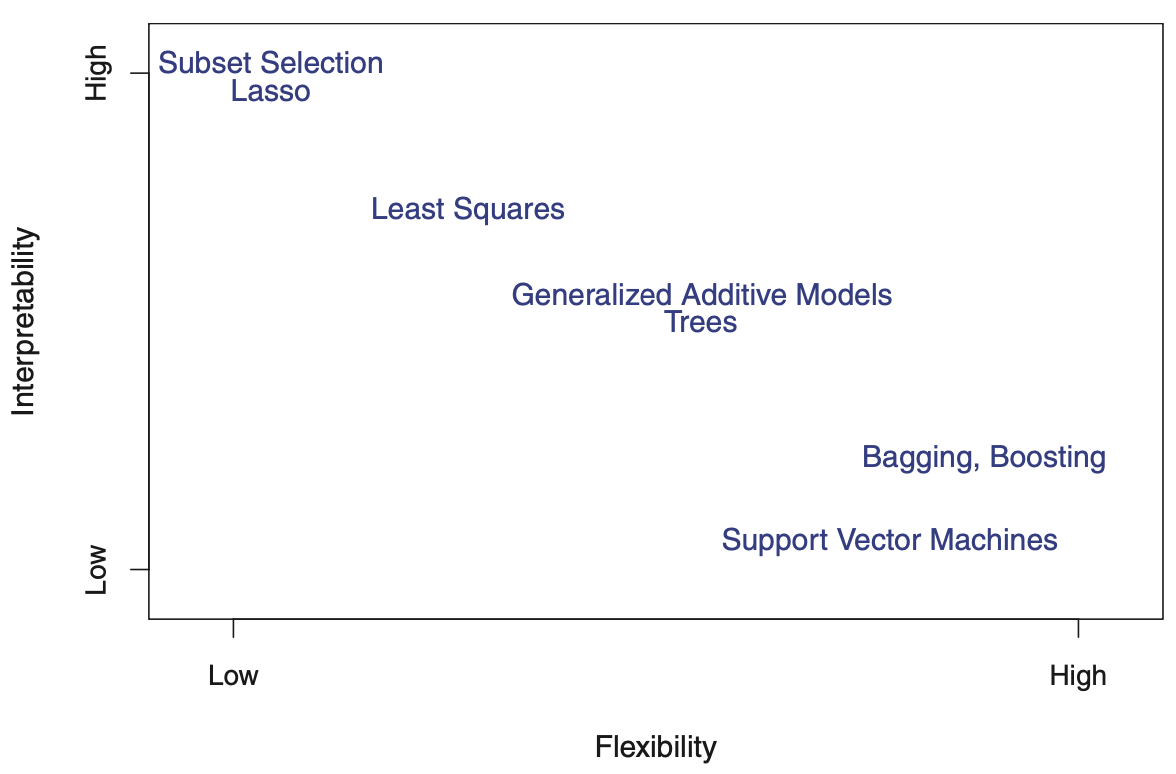
Bildquelle: James et al. (2013): Introduction to Statistical Learning

Performance von Trainings- vs. Testdaten

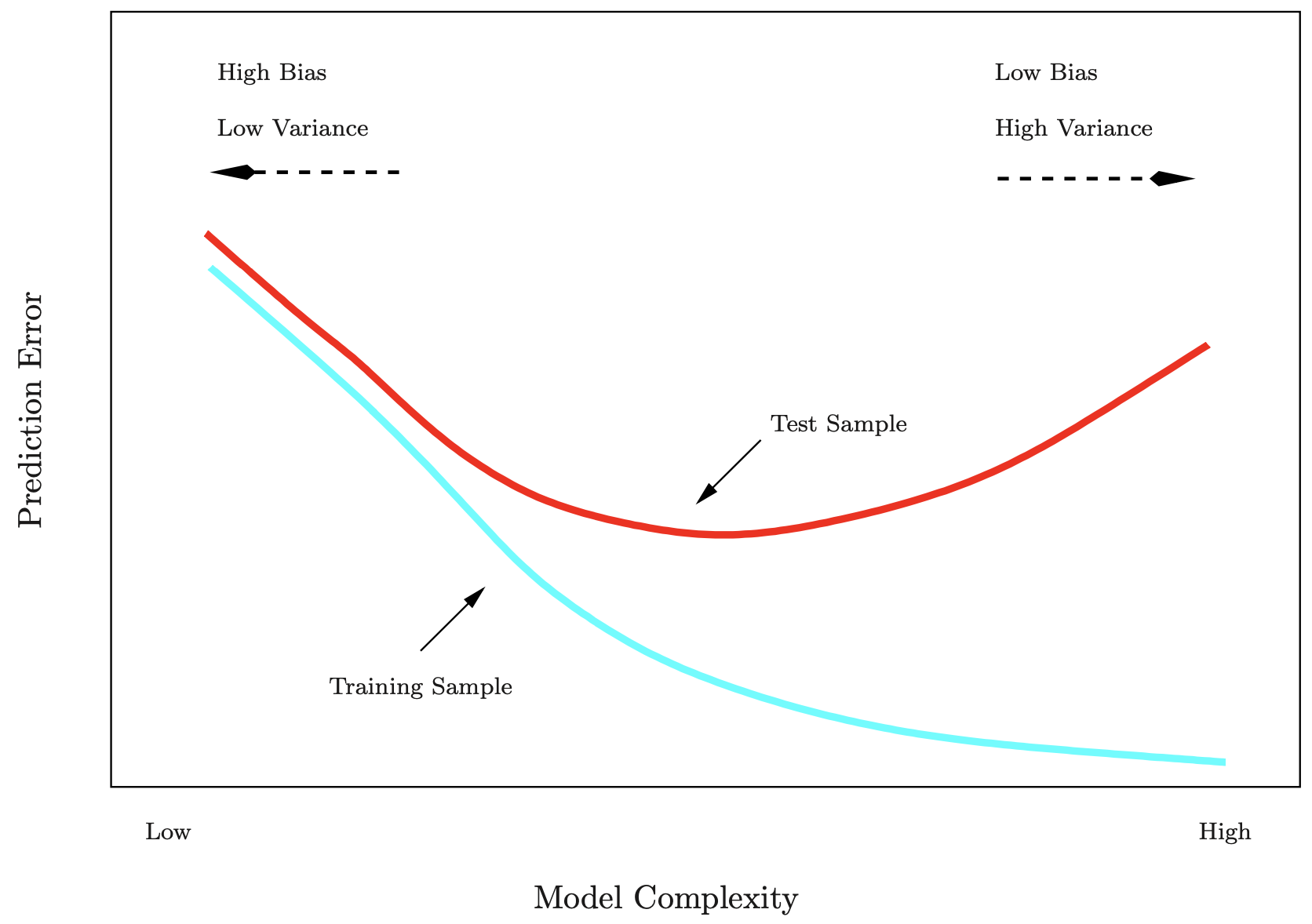
Die Trainingsfehlerrate (MSE_{train}) unterscheidet sich oft erheblich von der Testfehlerrate (MSE_{test}). Insbesondere bei sehr flexiblen Modellen kann die Trainingsfehlerrate die Testfehlerrate drastisch unterschätzen.

Bildquelle: James et al. (2013): Introduction to Statistical Learning

Supervised Learning | Beliebte Methoden

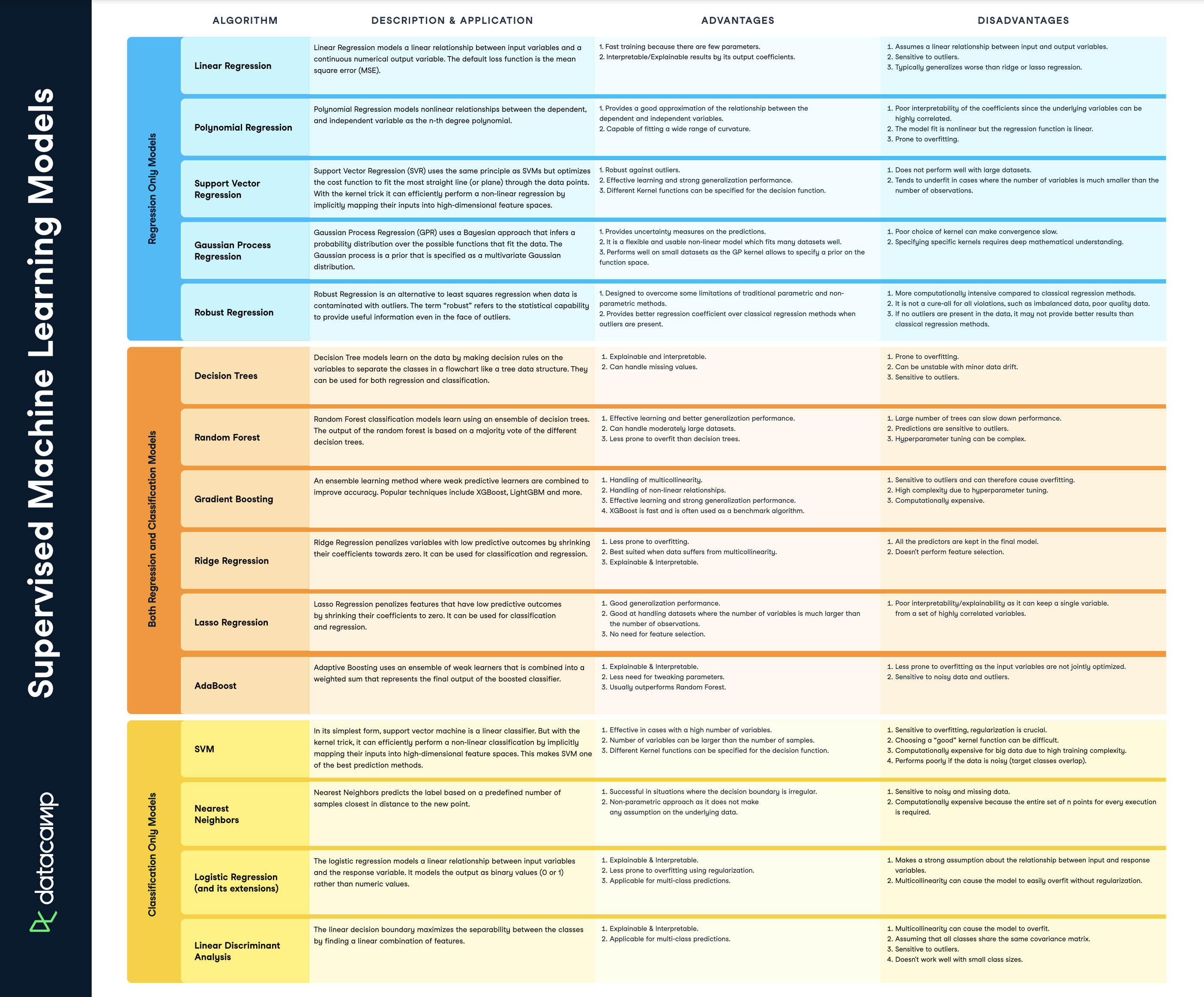
Download-link dieses Cheatsheets: [datacamp.com](https://www.datacamp.com/cheat-sheet/)

Polynomiale Regression: Eine Erweiterung der linearen Regression, bei der nichtlineare Zusammenhänge durch die Einführung von polynomialen Funktionen der unabhängigen Variablen modelliert werden. Dies ermöglicht die Anpassung von Kurven an die Daten.

Ridge Regression (L2 Regularisierung): Eine Regressionsmethode, die eine L2-Regularisierung (ridge penalty) verwendet, um Überanpassung zu verhindern. Sie ist besonders nützlich, wenn es Multikollinearität zwischen den unabhängigen Variablen gibt.

Lasso Regression (L1 Regularisierung): Ähnlich wie Ridge Regression, aber verwendet L1-Regularisierung, um einige Koeffizienten auf genau null zu schrumpfen. Dies ermöglicht automatische Feature-Auswahl.

Elastische Netz Regression: Kombiniert die Ridge- und Lasso-Regression durch Hinzufügen von beiden Regularisierungstermen zur Zielfunktion. Es bietet einen Kompromiss zwischen den beiden Ansätzen.

Support Vector Regression (SVR): Eine Regressionsmethode, die auf den Prinzipien der Support Vector Machines basiert. SVR zielt darauf ab, eine Hyperplane so zu platzieren, dass der größtmögliche Abstand zwischen den Datenpunkten und der Hyperplane erreicht wird.

Entscheidungsbaumregression: Verwendet Entscheidungsbäume, um nichtlineare Zusammenhänge in den Daten zu erfassen. Der Baum wird in einem Top-Down-Ansatz erstellt, indem die Daten in Partitionen aufgeteilt werden.

Random Forest Regression: Eine Ensemble-Methode, die mehrere Entscheidungsbäume kombiniert, um die Vorhersagegenauigkeit zu verbessern und Überanpassung zu reduzieren.

Gradient Boosting Regression: Eine Ensemble-Methode, bei der schwache Modelle schrittweise hinzugefügt werden, wobei jeder neue Baum auf den Fehlern der vorherigen Modelle basiert. XGBoost und LightGBM sind Beispiele für Gradient-Boosting-Methoden.

Live-Demo in R

Zurück zu Primärdaten

Aber fangen wir erstmal wieder mit kleineren Datensätzen aus (eigenen) Datenerhebungen an …

Quelle: chatGPT

Zur Erinnerung…

Häufiger Designtyp: CRD

und entsprechende (parametrische) Analysen

Vollständig randomisiertes Design - Completely Randomised Design (CRD)

• Alle Versuchseinheiten sind unabhängig und werden den Kombinationen an Behandlungsstufen zufällig zugeordnet.
• Unterscheidet in
  • 1 (fester) Faktor, 2 Gruppen → t-Test (oder 1-way ANOVA)
  • 1 (fester) Faktor, mehrere Gruppen → 1-way ANOVA (oder Regression)
  • 2 (feste) Faktoren, gekreuzt → 2-way crossed ANOVA
  • 1 (fester) Faktor mit Unterproben (Pseudoreplikation) → 2-way nested ANOVA / LME
  • 1 (fester) Faktor, 1 Kovariate → ANCOVA
  • 1 (zufälliger) Faktor, 1 Kovariate → LME

Feste vs. zufällige Effekte

Feste Effekte → Behandlungseffekte

• Die meisten Standardtests gehen von festen Faktoren aus.
• Die einzelnen Faktorstufen beziehen sich auf den Mittelwert von Y.

Zufällige Effekte → biologische/technische Eff.

• Die einzelnen Faktorstufen beziehen sich auf die Varianz von Y.
• Zufällige Effekte sind meist weniger interessant.
• Haben meist viele Faktorstufen

Auswahl des Effekttypen

Fragen, die Sie sich stellen sollten	Fest	Zufällig
Interessiert an den Unterschieden zwischen den Faktorstufen?	☑️︎
Ist der Faktor ein Behandlungseffekt?	☑️
Sind die Faktorstufen informativ?	☑️
Repräsentieren die Faktorstufen experimentelle Interventionen?	☑️
Sind die Faktorstufen speziell ausgewählt?	☑️
Kommen alle Stufen des Faktors im Experiment vor?	☑️
Kommen die Faktorstufen von der gleichen Population?		☑️
Gibt es viele Faktorstufen?		☑️
Soll auf andere Faktorstufen, die nicht im Experiment vorkommen, verallgemeinert werden?		☑️
Gibt es ein verschachteltes (nested) oder hierarchisches (Sub)sampling?		☑️

Quelle: Lazic (2016) Experimental Design for Laboratory Biologists

Completely Randomised Design (CRD)

Alle experimentellen Einheiten sind unabhängig und können zufällig allen Kombinationen von Behandlungsstufen zugeteilt werden.

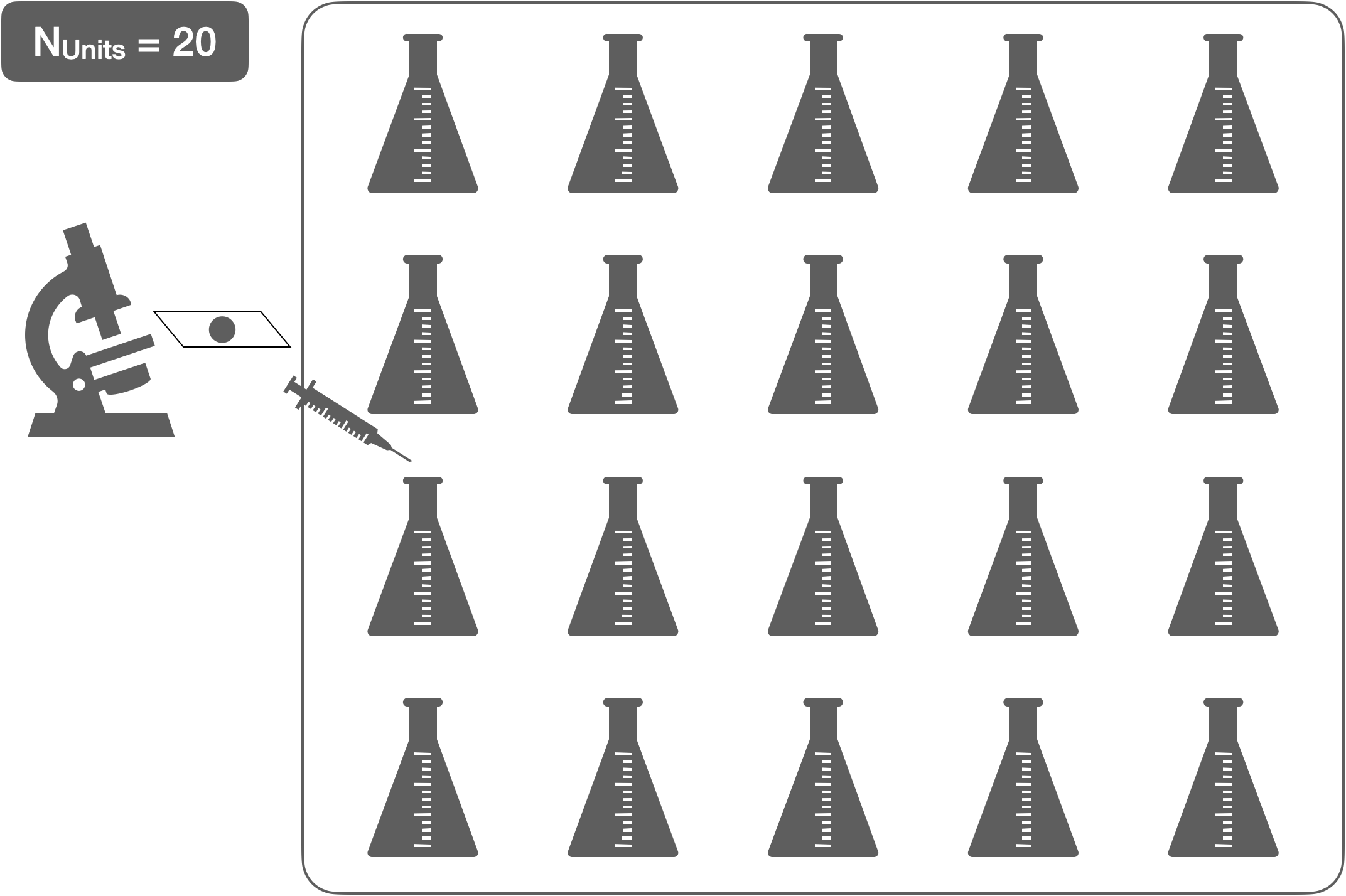
CRD - 2 gekreuzte Faktoren (je 2 Gruppen)

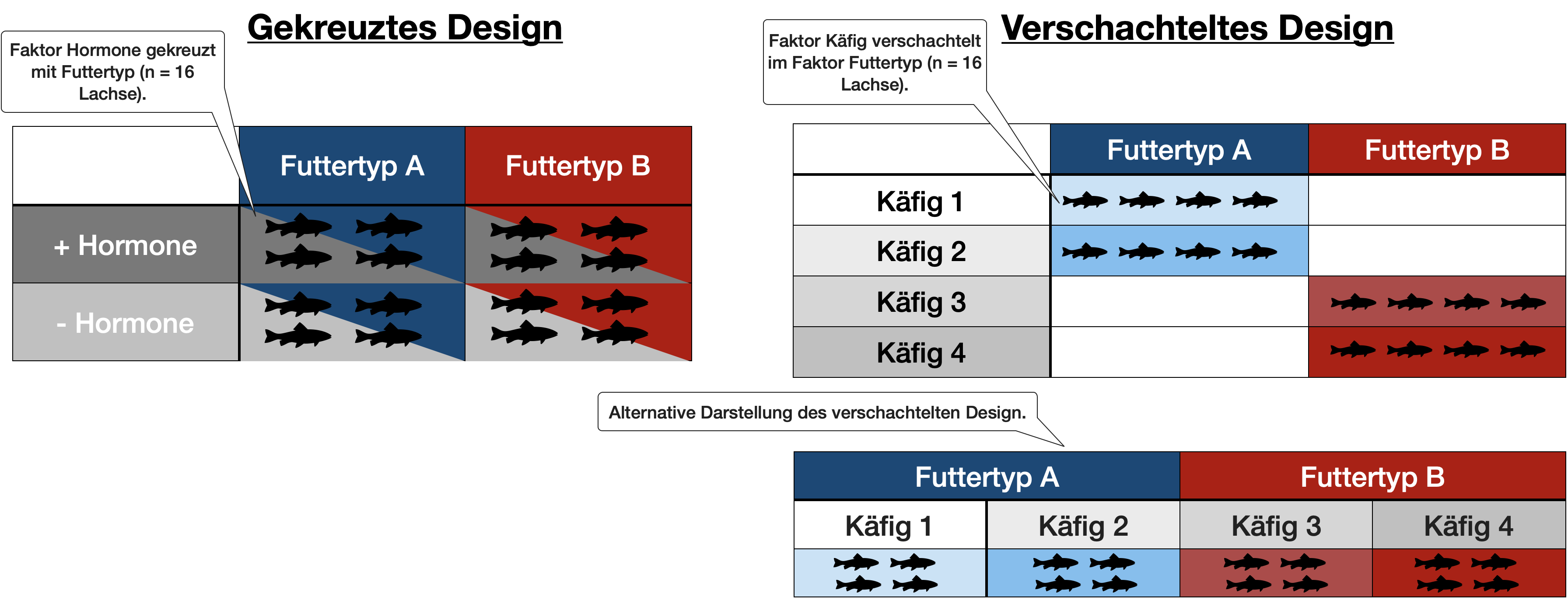
Gekreuztes Design

• N: 20 (Erlenmeyerkolben)
• n: 5 (EK pro Dosis/Typ)
• Ergebnis: Zellzahl
• Behandlungseffekte:
  • Dosis (fest) = {0, 100}
    
  • Typ (fest) = {1, 2}
• Analyse: 2-way crossed/factorial ANOVA

CRD - 1 Faktor (2 Gruppen) mit Unterprobe

Verschachteltes Design

• N: 8 (Exp. Units: Erlenmeyerkolben)
• n: 3 (Objektträger als Unterproben pro EK)
• Ergebnis: Zellzahl
• Effekte:
  • Behandlungseff.: Dosis (fest) = {0, 100}
  • Technischer Eff.: EK (zufällig) = {1,2,3,..,8}
• Analyse: 2-way nested ANOVA (oder ‘summary measure’ analysis)
• Freiheitsgrade:

\begin{align*} \text{Ergebnis} &= \text{Dosis} + \text{Fehler}\\ \text{(N - 1)} &= \text{(p - 1)} + \text{(N - p)}\\ \text{(7)} &= \text{(1)} + \text{(6)} \end{align*}

Vergleich beider Designs

CRD - 1 Faktor mit Unterprobe | Ansätze

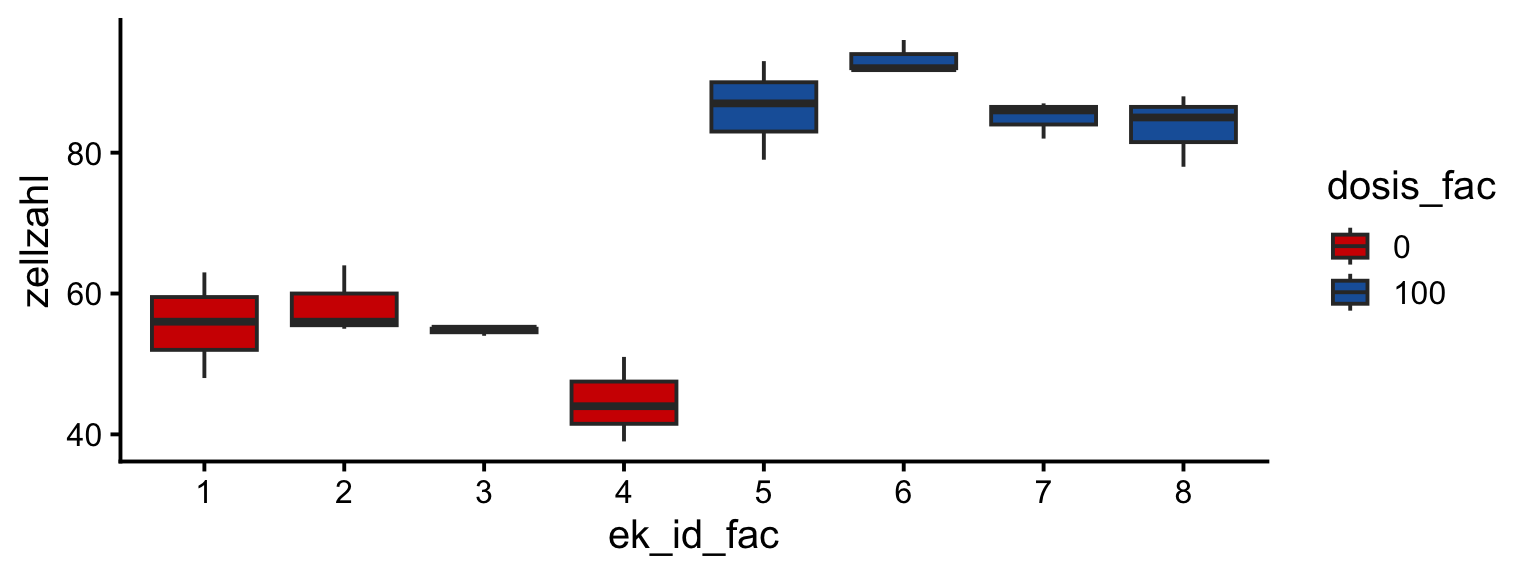
• Falscher Ansatz:
  • 1-faktorielle ANOVA, ohne Berücksichtigung der Pseudoreplikation
• Richtige Ansätze:
  • 1-faktorielle ANOVA mit gemittelten Unterprobewerte (‘summary measure’ analysis).
  • Lineares Gemischtes Modell (LME) mit dem R Paket nlme (oder lme4).

CRD - 1 Faktor mit Unterprobe | Falscher Ansatz

1-faktorielle ANOVA

aov(zellzahl ~ dosis_fac, df) |> summary()

            Df Sum Sq Mean Sq F value   Pr(>F)    
dosis_fac    1   6834    6834   167.1 9.38e-12 ***
Residuals   22    900      41                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• Die Freiheitsgerade der Residuen betragen hier 22!
• Die FG zur Berechnung des F- und p-Werts der Behandlungsvariable (Dosis) dürfen nicht höher sein als die experimentellen Einheiten selbst (hier 8).
• Dadurch ist der F-Wert viel höher und der p-Wert viel niedriger als korrekt wäre.

CRD - 1 Faktor mit Unterprobe | Ansatz 1

1-faktorielle ANOVA mit gemittelten Unterprobewerten

df_sm <- df |>
  group_by(ek_id_fac, dosis_fac) |>
  summarise(zellzahl_means = mean(zellzahl))

aov(zellzahl_means ~ dosis_fac, df_sm) |> summary()

            Df Sum Sq Mean Sq F value   Pr(>F)    
dosis_fac    1   2278  2278.1   83.87 9.54e-05 ***
Residuals    6    163    27.2                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• Hier wird das Problem der Pseudoreplikation durch die Mittelwertbildung gelöst.

Übungen

Übungswoche 1

Summary Measure Analysis’ der DS2 Fallstudie

Vorbereitung @home (s. Handbuch)

• Auffrischungsquiz (siehe Moodle)
• Fallstudiendaten zu Aufgabe 2.2 (Mehrstichprobentest) vorbereiten:
  • Neues Skript bzw. Notebook erstellen.
  • Benötigte Daten in R laden und aufbereiten.
  • Mittelwertbildung der Kronblattbreite für jede Pflanze.

Fragen..??

Total gelangweilt?

Dann testen Sie doch Ihr Wissen in folgendem Abschlussquiz…

Abschlussquiz

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de


Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.