Kurseinführung und 2-faktorielle Varianzanalyse (Teil 1)

DS3 - Vom experimentellen Design zur
explorativen Datenanalyse & Data Mining

Saskia Otto

Universität Hamburg, IMF

Wintersemester 2023/2024

Durchführung wissenschaftlicher Studien

Von den Primärdaten (experimentelles Design) zu den Sekundärdaten (Data Mining)

‘LEARNING’ vs. ‘Confirming Experiments’

Lernende (explorative) Experimente

• Hat das Medikament toxische Nebenwirkungen (in welcher Dosis, über welchen Zeitraum, in welchem Gewebe)?
• Das Ziel ist etwas Neues zu lernen.
• Hypothese ist allgemeiner und ein statistischer Test ist weniger wichtig
• Typisches Beispiel in der Biologie: ‘High-throughput screening’ in den Omics Wissenschaften.

Emutlu et al. (2012): ¹⁸O-assisted dynamic metabolomics
for individualized diagnostics and treatment of human
diseases, Croat Med J 53(6): 529–534

Themenübersicht des Moduls

1. Gekreuzte 2-faktorielle Varianzanalyse
2. Verschachtelte 2-faktorielle Varianzanalyse
3. Kovarianzanalyse, multiple lineare Regression & Modellselektion
4. Entscheidungsbäume für Regressions- und Klassifikationsverfahren
5. EDA und Resampling Techniken
6. Open Science und RMarkdown bzw. Quarto
7. Logistische Regression
8. Multivariate Verfahren: Clusteranalyse und Ordination
9. Datenbanken und Abgreifen von Sekundärdaten aus R

Statistik in Zeiten der Computer-Ära

Klassische Inferenzstatistik

• Frequentistische Inferenz
• Bayes’sche Inferenz
• Fisher’sche Inferenz und die Maximum-Likelihood-Schätzung
• Parametrische Modelle (Regression, ANOVA, ANCOVA)

Frühe Methoden des Computerzeitalters

• Empirische Bayes Methode
• James-Stein-Schätzung und Ridge-Regression
• Generalisierte Lineare und Additive Modelle (GLM, GAM)
• Entscheidungsbäume CART (Classification und Regression Trees)
• Überlebensanalyse (survival analysis) und Erwartungs-Maximierungs-Algorithmus
• Jackknife und Bootstrap Methoden
• Markov Chain Monte Carlo
• ARIMA Modelle

Methoden des 21. Jahrhunderts

• Großskalige Hypothesentests und Falscherkennungsraten
• Sparse Modeling und Lasso Regression
• Random Forests und Boosting
• Neuronale Netzwerke und Deep Learning
• Support-Vector Machines und Kernel Methoden
• Empirische Bayes Schätzstrategien

Aus Efron & Hastie (2016)
Computer Age Statistical
Inference: Algorithms,
Evidence, and Data Science
Link zum Buch: hier

Empfohlene Literatur

• Bärlocher, F. (1999): Biostatistik - Praktische Einführung in Konzepte und Methoden. Thieme Verlag, 206 S.
• Quinn, G.P., Keough, M.J. (2002): Experimental Design and Data Analysis for Biologists, Cambridge, UK, 553 S.
• Michael J. Crawley (2013). The R Book, Wiley, 945 S. Eine PDF Version ist Online hier
  • Sehr umfangreiches Buch (fast 1000 Seiten!). Deckt sowohl grundlegende Statistiken als auch viele verschiedene statistische Modellierungsansätze ab (die den Rahmen dieses Kurses sprengen würden).
• Alain F. Zuur, Elena N. Ieno, Neil J. Walker, Anatoly A. Saveliev, Graham M. Smith (2009): Mixed Effects Models and Extensions in Ecology with R, Springer Science+Business Media, LLC, NewYork, U.S.A., 574 S. → https://highstat.com
  • Dieses Buch befasst sich mit einfachen linearen Regressionsmodellen und ihren Grenzen und beschreibt alternative Ansätze (Anhang A ist ein guter Anfang!). Es enthält verschiedene ökologische Fallstudien, in denen der EDA-Zyklus (Exploratory Data Analayis) gut beschrieben ist.
• Gareth James, Daniela Witten, Trevor Hastie Robert Tibshirani (2013): An Introduction to Statistical Learning with Applications in R, Springer Science+Business Media, 426 S.

Zur Erinnerung…

Klassischer Weg in der
inferenziellen
Statistik

Schritt 1 | Wahl der Statistik

Beispiel einer Forschungshypothese

Die intraspezifische Streuung des Zugverhaltens ist bei Buchfinken kleiner als bei der Mönchsgrasmücke.

Buchfink

Mönchsgrasmücke

Zu vergleichender Parameter bzw. Kennwert

Die Varianz \(\sigma^2\) bzw. \(s^2\)

Bildquellen: Wikipedia (Buchfink unter CC BY-SA 2.5 Lizenz) und Mönchsgrasmücke unter CC0 Lizenz)

Schritt 2 | Formulierung der Hypothesen

Beispiel Zugverhalten

Die intraspezifische Streuung des Zugverhaltens ist bei Buchfinken kleiner als bei der Mönchsgrasmücke.

Buchfink

Mönchsgrasmücke

Hypothesen (einseitig)

• \(H_A: \sigma_{Buchfink}^2 < \sigma_{Mönchsgrasmücke}^2\)
• \(H_0: \sigma_{Buchfink}^2 \geq \sigma_{Mönchsgrasmücke}^2\)

Bildquellen: Wikipedia (Buchfink unter CC BY-SA 2.5 Lizenz) und Mönchsgrasmücke unter CC0 Lizenz)

Schritt 3 | Datenerhebung und -exploration

Beispiel Zugverhalten

Kenngröße	Buchfink	Mönchsgrasmücke
Mittelwert x̅	1800 km	3000 km
Standardabweichung s	±900 km	±1000 km
Stichprobengröße n	20	30

Buchfink

Mönchsgrasmücke

Wahl des statistischen Test | Schritt 4

Folgende grundlegende Fragen müssen beantwortet werden:

1. Welches Skalenniveau liegt vor (nominal, ordinal, metrisch)?
2. Wie viele Stichproben sollen verglichen werden (1, 2, ≥2)?
3. Was soll getestet werden (Abweichungen von einer Verteilung, einer erwarteten Häufigkeitsverteilung, einem Erwartungswert)?
4. Ermöglicht die Stichprobenverteilung die Anwendung parametrischer Verfahren, d.h. sind die Daten normal verteilt (und Varianzhomogen) (Schritt 3)?

Wahl des statistischen Test | Übersicht

Klassische Tests

Signifikanzniveau | Schritt 5

oder auch Irrtumswahrscheinlichkeit \(\alpha\)

• Wahrscheinlichkeit für die Ablehnung der \(H_0\), obwohl diese zutrifft (’bedingte Wahrscheinlichkeit, Fehler 1. Art).
• In der Statistik ist ein Ergebnis dann signifikant, wenn es unwahrscheinlich ist, dass es zufällig aufgetreten ist, vorausgesetzt, eine angenommene \(H_0\) ist wahr.
• Wenn das beobachtete Signifikanzniveau klein genug ist, wird die \(H_0\) verworfen.

Übliche Signifikanzwerte

• Signifikant: p ≤ 0.05
• Hoch signifikant: p ≤ 0.01
• Höchst signifikant: p ≤ 0.001
• Schwach signifikant: 0.05 ≤ p < 0.01
• Schwach nicht signifikant: 0.1 ≤ p < 0.05

Statistische Fehler 1. und 2. Art

Entscheidung	\(H_0\) trifft zu	\(H_0\) trifft nicht zu
\(H_0\) wird nicht abgelehnt	Richtige Entscheidung; kein Effekt nachgewiesen	\(\beta\)-Fehler; vorhandenen Effekt nicht nachgewiesen
\(H_0\) wird abgelehnt	\(\alpha\)-Fehler; Effekt nachgewiesen, den es nicht gibt	Richtige Entscheidung; vorhandenen Effekt nachgewiesen

Häufige Designtypen

und entsprechende (parametrische) Analysen

Vollständig randomisiertes Design - Completely Randomised Design (CRD*)

• Alle Versuchseinheiten sind unabhängig und werden den Kombinationen an Behandlungsstufen zufällig zugeordnet.
• Unterscheidet in
  • 1 Faktor, 2 Gruppen → t-Test (oder 1-way ANOVA)
  • 1 Faktor, mehrere Gruppen → 1-way ANOVA (oder Regression)
  • 2 Faktoren, gekreuzt → 2-way crossed ANOVA
  • 1 Faktor mit Unterproben (Pseudoreplikation) → 2-way nested ANOVA
  • 1 Faktor, 1 Kovariate → ANCOVA

Weitere Designs

• Randomisiertes Blockdesign (RBD)
• Design mit Messwiederholung (Repeated measures design - RM)
• Split-Plot-Design

Completely Randomised Design (CRD)

Alle experimentellen Einheiten sind unabhängig und können zufällig allen Kombinationen von Behandlungsstufen zugeteilt werden.

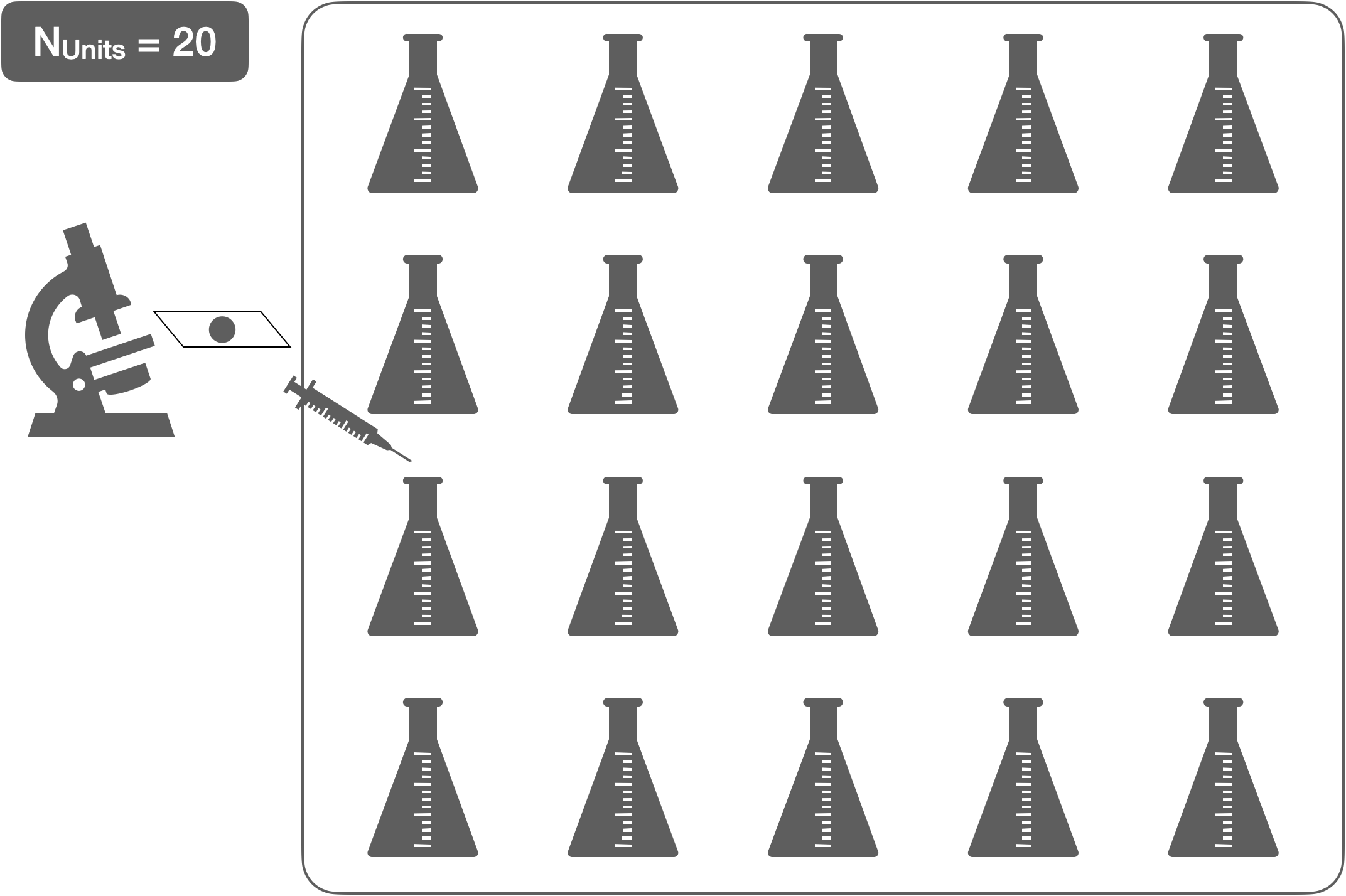
CRD - 1 Faktor (2 Gruppen)

Design

• N: 20 (Exp. Units: Erlenmeyerkolben)
• n: 10 (EK pro Dosis)
• Ergebnis: Zellzahl
• Behandlungseffekt: Dosis (fest) = {0, 100}
• Analyse: t-Test (oder 1-way ANOVA)
• Freiheitsgrade:

\[\begin{align*} \text{Ergebnis} &= \text{Dosis} + \text{Fehler}\\ \text{(N - 1)} &= \text{(p - 1)} + \text{(N - p)}\\ \text{(19)} &= \text{(1)} + \text{(18)} \end{align*}\]

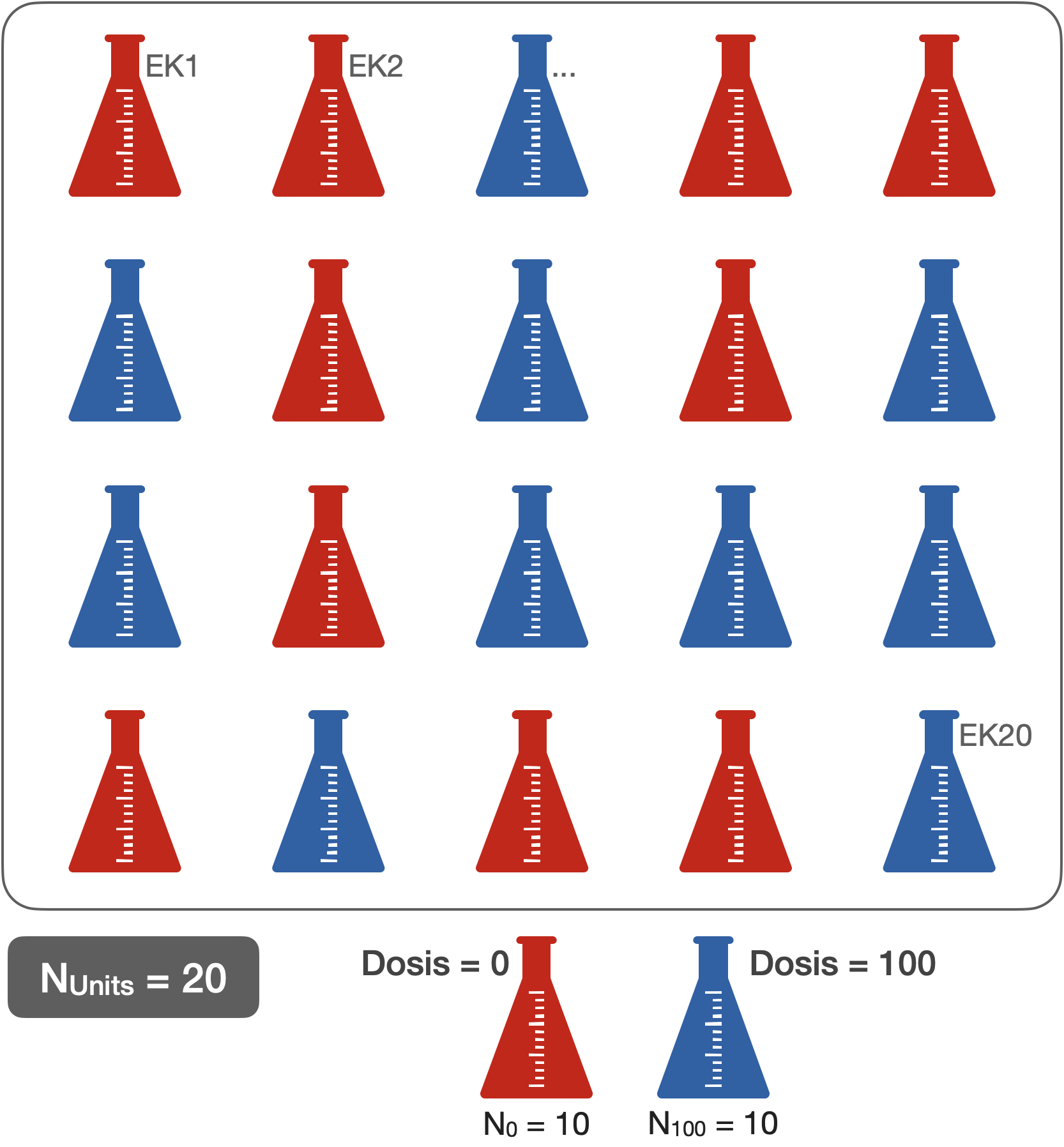
CRD - 1 Faktor (4 Gruppen)

Design

• N: 20 (Exp. Units: Erlenmeyerkolben)
• n: 5 (EK pro Dosis)
• Ergebnis: Zellzahl
• Behandlungseffekt: Dosis (fest) = {0,50,100,150}
• Analyse: 1-way ANOVA (oder Regression)
• Freiheitsgrade:

Dosis ist kategorial (ANOVA): \[\begin{align*} \text{Ergebnis} &= \text{Dosis} + \text{Fehler}\\ \text{(N - 1)} &= \text{(p - 1)} + (\text{N - p})\\ \text{(19)} &= \text{(3)} + (\text{16}) \end{align*}\]

Dosis ist kontinuierlich (Regression): \[\begin{align*} \text{Ergebnis} &= \text{Dosis} + \text{Fehler}\\ \text{(19)} &= \text{(1)} + (\text{18}) \end{align*}\]

CRD - 1 Faktor (4 Gruppen) | ANOVA Tabelle

Typische Tabelle einer 1-faktoriellen Varianzanalyse

CRD - 1 Faktor (4 Gruppen) | 1-way ANOVA

Ergebnis, wenn Dosis richtig als Faktor kodiert ist

aov(zellzahl ~ dosis_fac, df) |> summary()

            Df Sum Sq Mean Sq F value  Pr(>F)   
dosis_fac    3   9713    3238   7.424 0.00247 **
Residuals   16   6978     436                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Ergebnis, wenn Dosis fälschlicherweise numerisch kodiert ist

aov(zellzahl ~ dosis_num, df) |> summary()

            Df Sum Sq Mean Sq F value   Pr(>F)    
dosis_num    1   8817    8817   20.16 0.000283 ***
Residuals   18   7874     437                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

CRD - 2 gekreuzte Faktoren (je 2 Gruppen)

Gekreuztes Design

• N: 20 (Erlenmeyerkolben)
• n: 5 (EK pro Dosis/Typ)
• Ergebnis: Zellzahl
• Behandlungseffekte:
  • Dosis (fest) = {0, 100}
    
  • Typ (fest) = {1, 2}
• Analyse: 2-way crossed/factorial ANOVA

CRD - 1 Faktor (2 Gruppen) mit Unterprobe

Verschachteltes Design

• N: 8 (Exp. Units: Erlenmeyerkolben)
• n: 3 (Objektträger als Unterproben pro EK)
• Ergebnis: Zellzahl
• Effekte:
  • Behandlungseff.: Dosis (fest) = {0, 100}
  • Technischer Eff.: EK (zufällig) = {1,2,3,..,8}
• Analyse: 2-way nested ANOVA (oder ‘summary measure’ analysis)
• Freiheitsgrade:

\[\begin{align*} \text{Ergebnis} &= \text{Dosis} + \text{Fehler}\\ \text{(N - 1)} &= \text{(p - 1)} + \text{(N - p)}\\ \text{(7)} &= \text{(1)} + \text{(6)} \end{align*}\]

CRD - Komplexe verschachtelte Designs

Beispiel: Räumliche Variabilität von Blattlausdichten

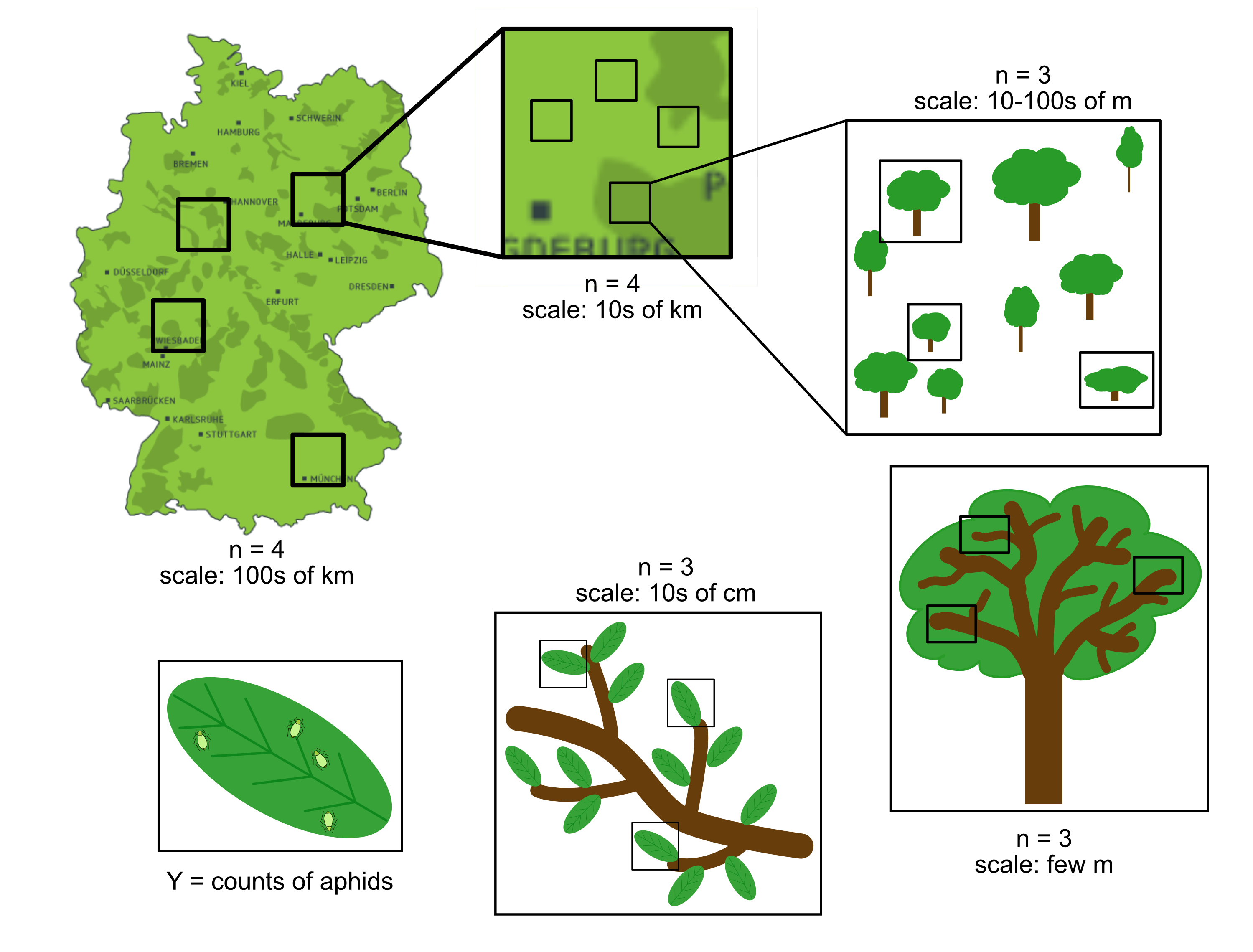
• Gerade bei räumlichen und zeitlichen Feldstudien ist das Beprobungsdesign oft stark verschachtelt.
• → Der größte Beprobungsaufwand sollte auf der Skala mit der höchsten Varianz erfolgen (viele Wiederholungen)!

Vergleich beider Designs

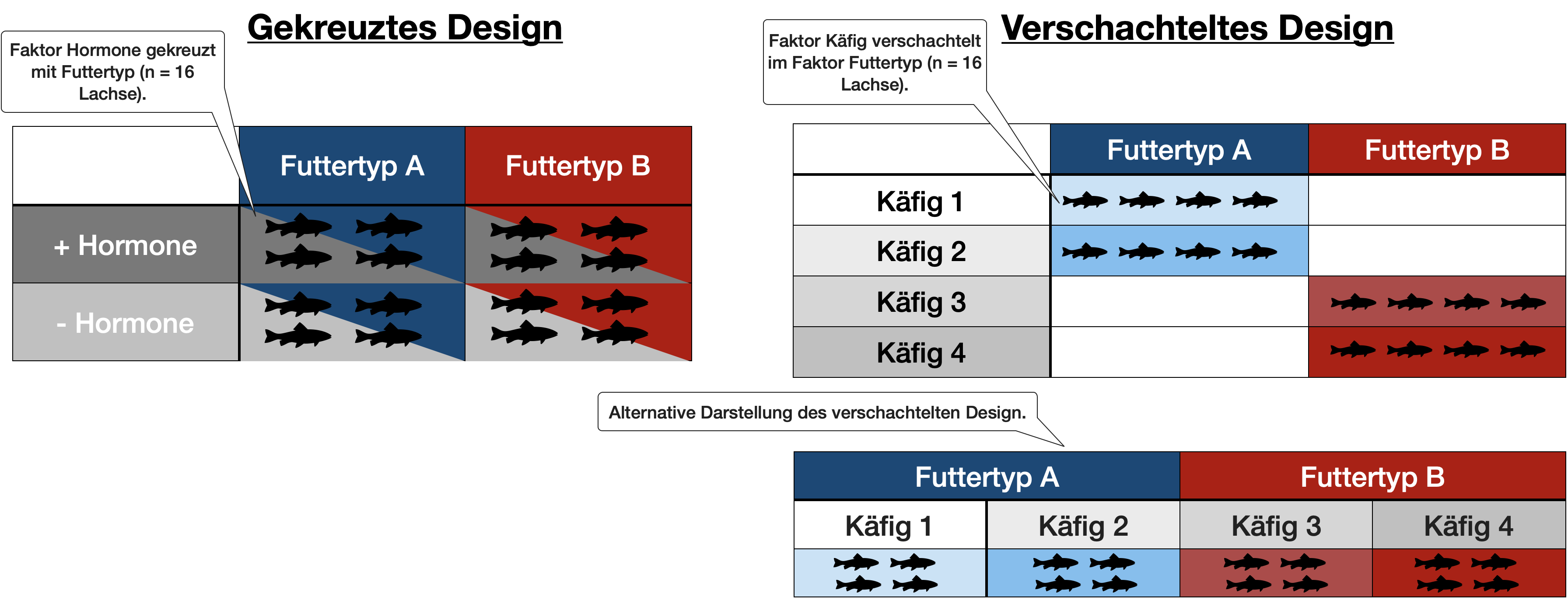
Falsche Anwendung

Aber wie berechnen wir ein solches gekreuztes Design mit 2 Faktoren?

2-faktorielle Varianzanalyse mit gekreuzten Faktoren

Napfschnecken Versuch

Qinn (1988) untersuchte die Auswirkungen der Jahreszeit und der Dichte der adulten Tiere auf die Fruchtbarkeit von Napfschnecken (Siphonaria diemenensis).

Antwortvariable Y: mittlere Anzahl der gelegten Eimassen pro Napfschnecke

Beispiel ist aus Kapitel 9.2 in Quinn & Keough (2002): Experimental Design and Data Analysis for Biologists

---

• Die Napfschnecken (ca. 10 mm Schalenlänge) waren in 225 cm2 großen Edelstahlnetzen eingeschlossen, die an der felsigen Plattform befestigt waren. Es gab acht Behandlungskombinationen (vier Dichten zu jeder der beiden Jahreszeiten) und drei Wiederholungen pro Behandlungskombination.
• Gekreuztes Design da alle vier Dichten in beiden Jahreszeiten verwendet wurden.
• Eine der wichtigsten Fragen, die bei diesem Versuch gestellt wurden, war, ob die Auswirkung der Dichte auf die Anzahl der Eimassen pro Napfschnecke von der Jahreszeit abhängt. Quinn (1988) sagte voraus, dass die Auswirkung der Dichte im Sommer/Herbst, wenn die Algennahrung knapp ist, größer sein würde als im Winter/Frühling, wenn die Algennahrung reichhaltiger ist.

Lineares ANOVA Model

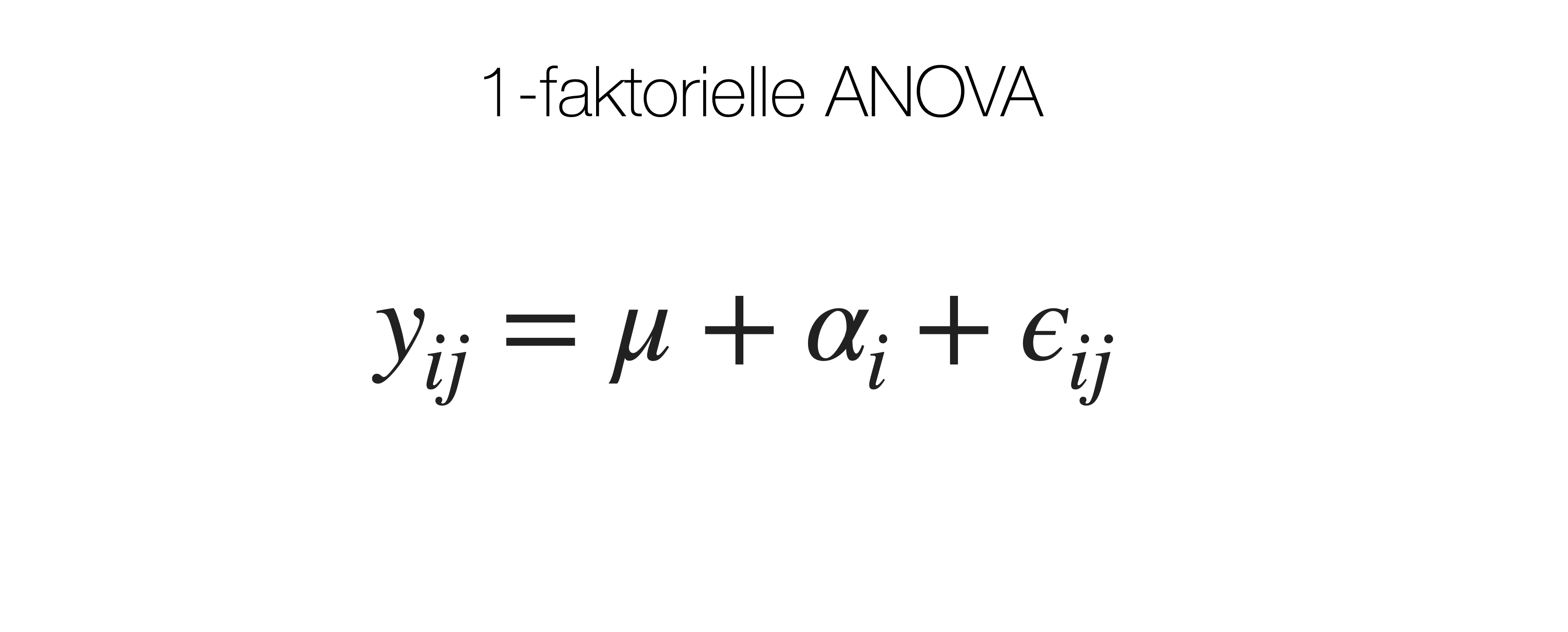
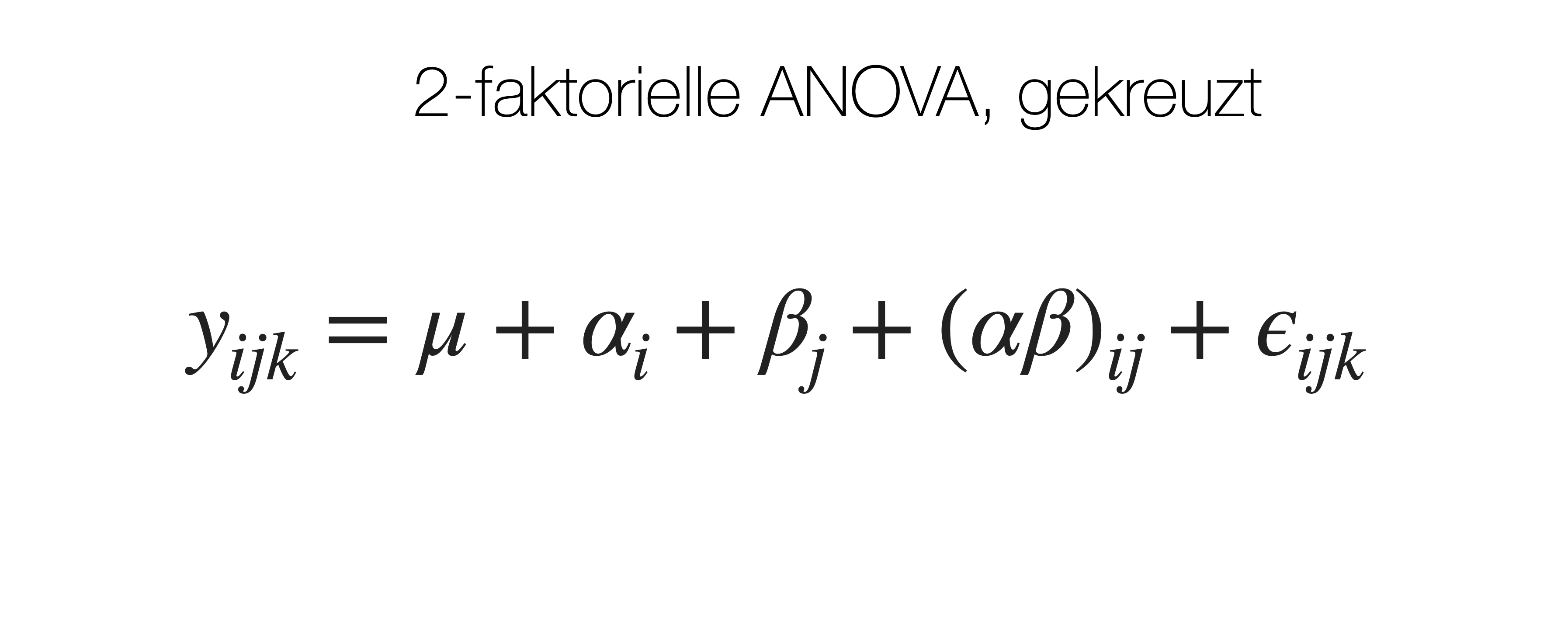
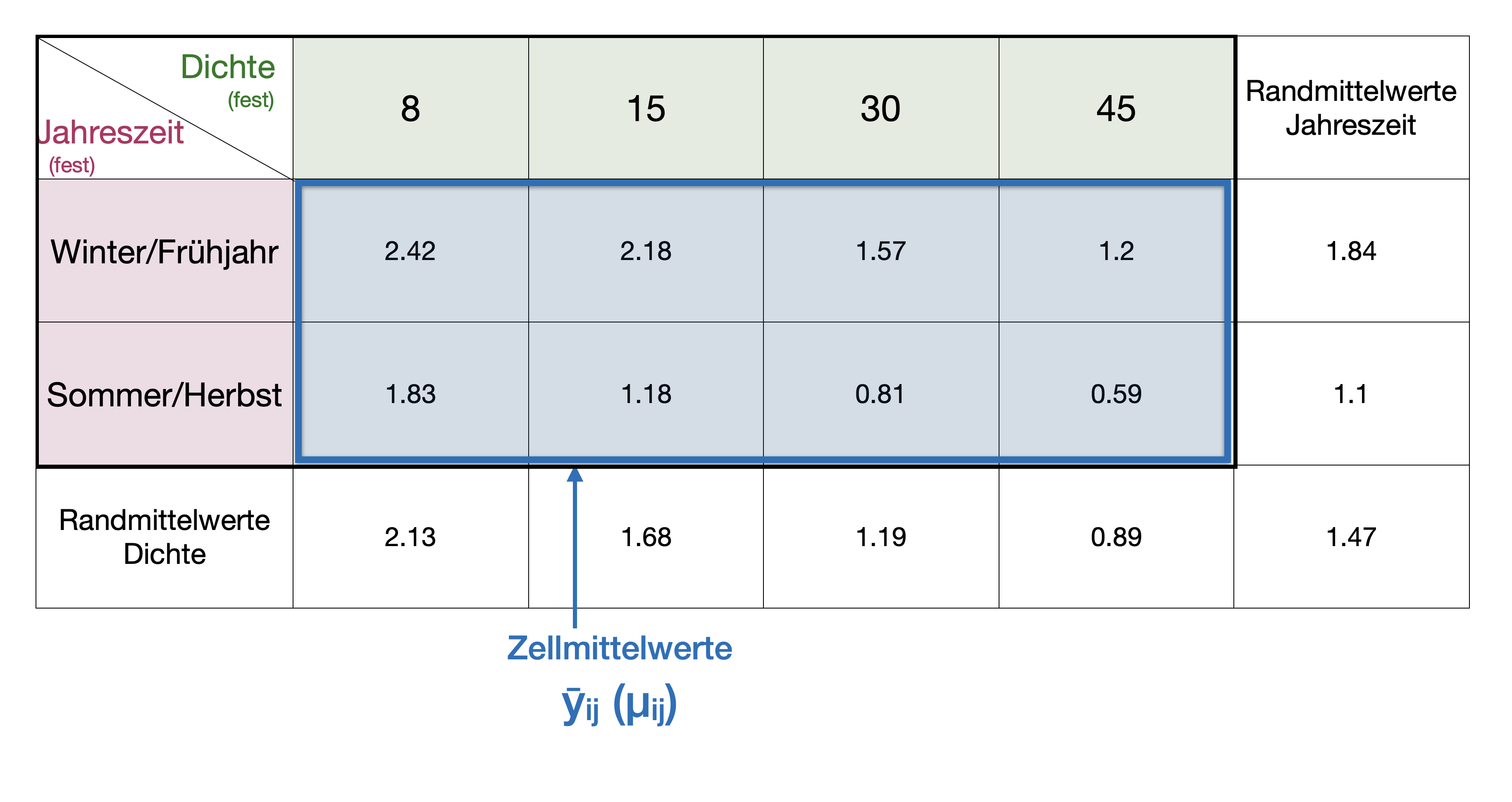
Napfschnecken Versuch | Zellmittelwerte

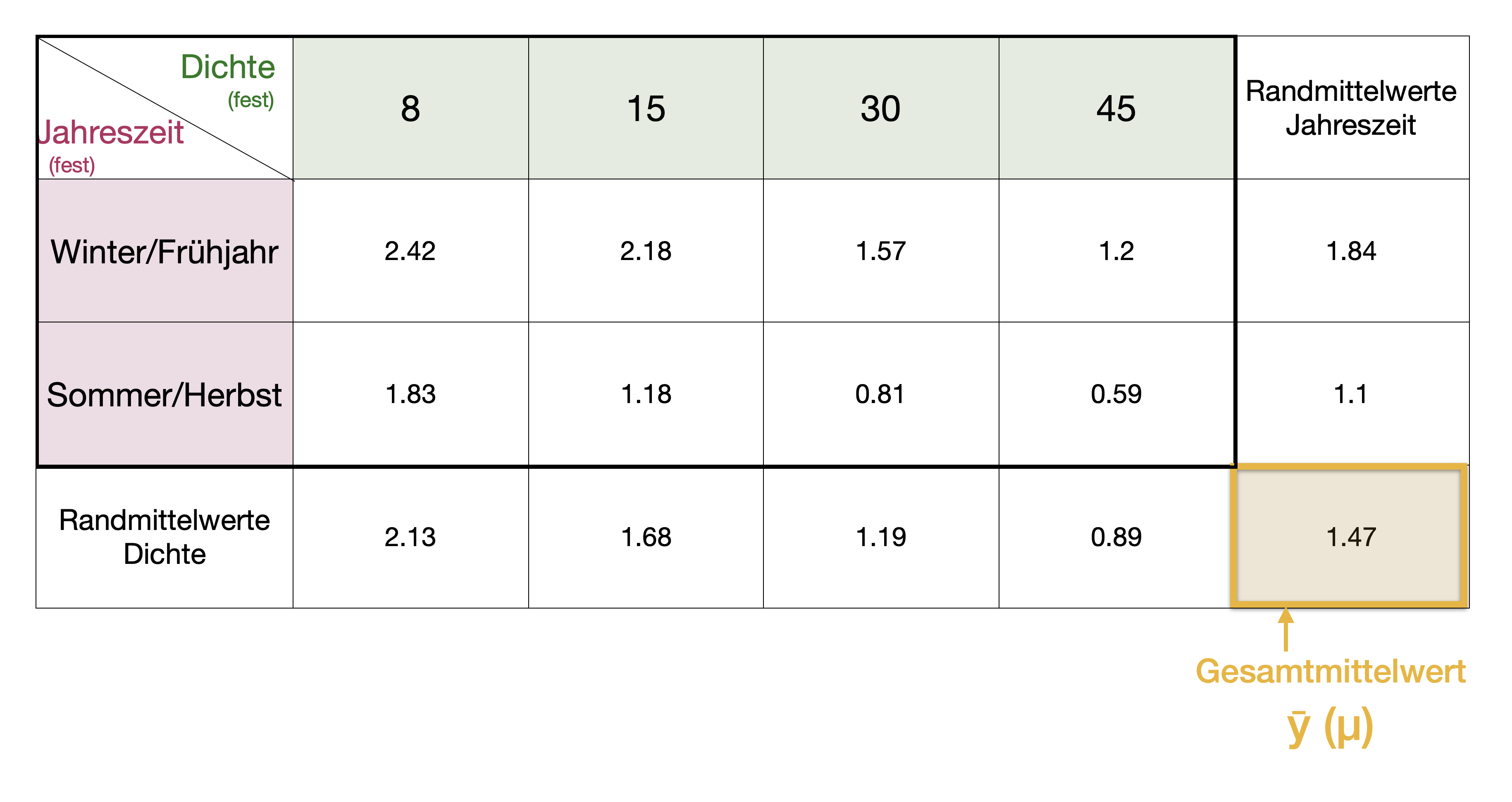
Napfschnecken Versuch | Gesamtmittelwert

Napfschnecken Versuch | Randmittelwerte

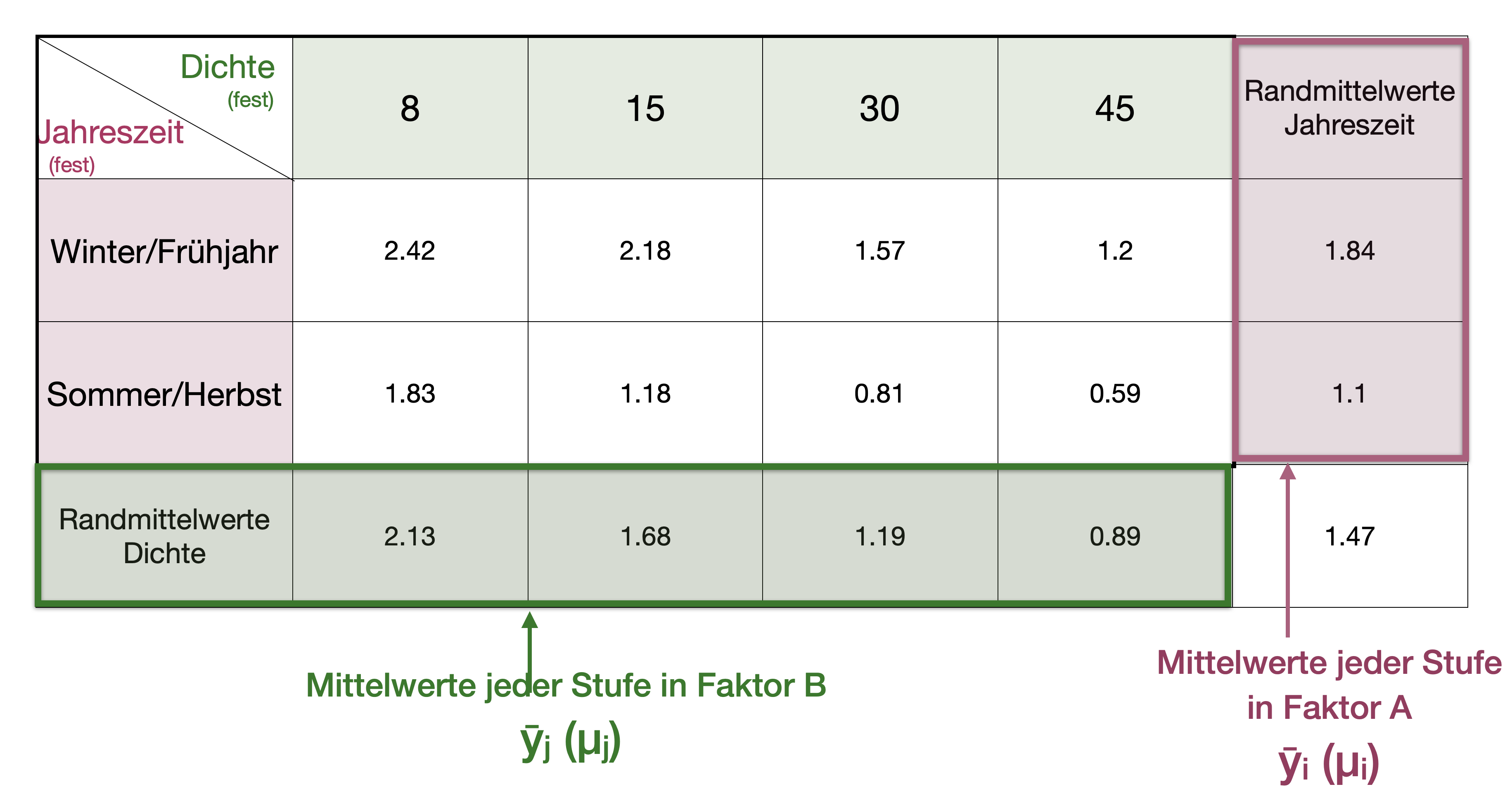
Hypothesen der beiden Haupteffekte

Interaktionen | 1

• Wenn die Wirkung eines Faktors von der Höhe eines anderen Faktors abhängt, liegt eine Wechselwirkung vor.
• H0 einer 2-Wege-Interaktion: keine Wechselwirkung zwischen Faktor A und Faktor B
  • Die Auswirkungen von Faktor A und Faktor B sind unabhängig voneinander.
  • Keine gemeinsame Wirkung von A & B.
  • \(\alpha\beta_{ij}= 0\) bzw. \(\mu_{ij}-\mu_i-\mu_j-\mu=0\)

Interaktionen

Wenn eine Wechselwirkung vorliegt,

ist es schwierig, den Haupteffekt und die marginalen Mittelwerte zu prüfen.

\(\Rightarrow\) Zuerst H0 auf keine Interaktion testen: Wenn nicht signifikant, Haupteffekte testen!

\(\Rightarrow\) Falls signifikant, untersuchen Sie jeden Faktor separat innerhalb der Stufen des anderen Faktors (paarweise Vergleiche!)

Wenn Sie Interaktionsterme einbeziehen wollen,

müssen auch die Hauptterme und alle untergeordneten Terme einbezogen werden!!

Y = A + B + C + AB vs. Y = A + C + AB

Interaktionen | Mögliche Effekte

Interaktionen | Grafisch explorieren

Hier ein Beispiel mit einfachen Boxplots:

ANOVA Tabelle bei 2 gekreuzten Faktoren

Zur Erinnerung | Feste vs. zufällige Effekte

Feste Effekte → Behandlungseffekte

• Die meisten Standardtests gehen von festen Faktoren aus.
• Die einzelnen Faktorstufen beziehen sich auf den Mittelwert von Y.

Zufällige Effekte → biologische/technische Eff.

• Die einzelnen Faktorstufen beziehen sich auf die Varianz von Y.
• Zufällige Effekte sind meist weniger interessant.
• Haben meist viele Faktorstufen

Berechnung der F-Werte

Interpretation der Ergebnisse

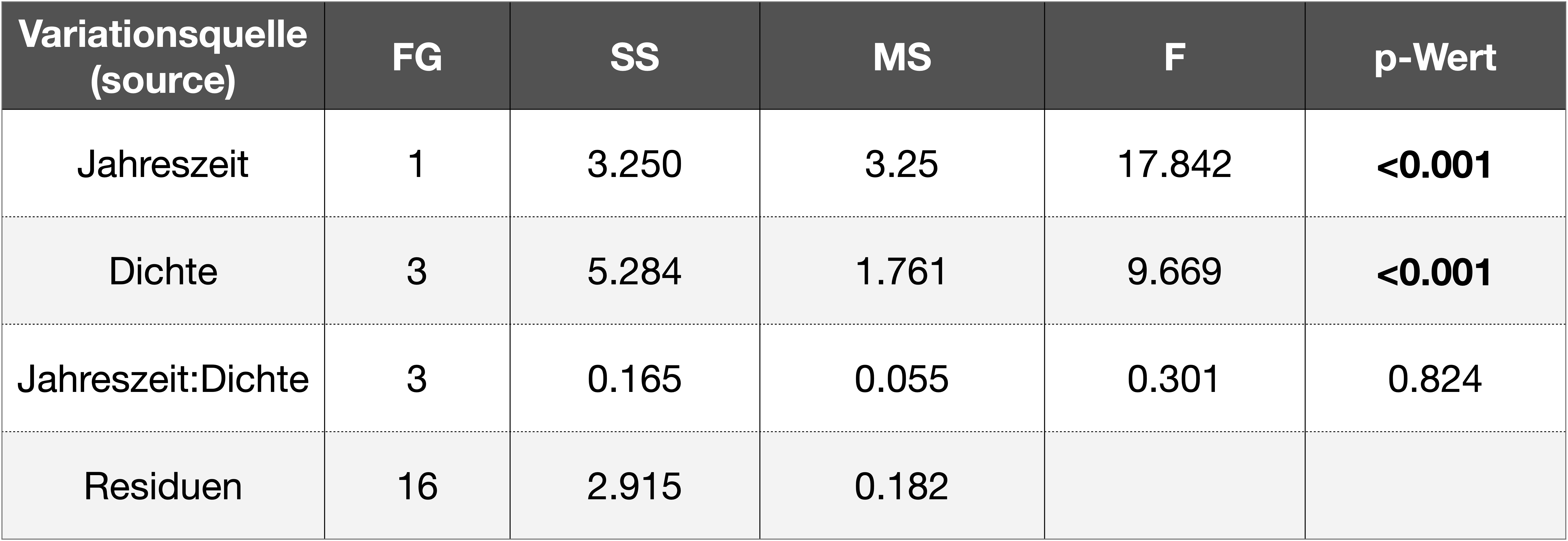
\(\Rightarrow\) Es gibt keine signifikante Interaktion.

\(\Rightarrow\) Es gibt einen sign. Effekt der Jahreszeit und der Dichte auf die Fruchtbarkeit von Napfschnecken (Siphonaria diemenensis).

Durchführung in R | 1

ANOVA mit Interaktion

mod1 <- aov(eggs ~ season + density + season:density, data = sipho1)
summary(mod1)

               Df Sum Sq Mean Sq F value   Pr(>F)    
season          1  3.250   3.250  17.842 0.000645 ***
density         3  5.284   1.761   9.669 0.000704 ***
season:density  3  0.165   0.055   0.301 0.823955    
Residuals      16  2.915   0.182                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Kurznotation für Interaktionen

aov(eggs ~ season * density, data = sipho1)

Durchführung in R | 2

ANOVA ohne Interaktion

mod2 <- aov(eggs ~ season + density, data = sipho1)
summary(mod2)

            Df Sum Sq Mean Sq F value   Pr(>F)    
season       1  3.250   3.250   20.05 0.000258 ***
density      3  5.284   1.761   10.87 0.000223 ***
Residuals   19  3.079   0.162                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Modelldiagnostik

par(mfrow = c(2,2))
plot(mod2)

Interaktion visualisieren

par(mfrow=c(1,2))
interaction.plot(sipho1$season, sipho1$density, sipho1$eggs)
interaction.plot(sipho1$density, sipho1$season, sipho1$eggs)

Effektgröße

• Ein Wert, mit dem Sie feststellen können, wie stark sich Ihre unabhängige Variable (X) auf die abhängige Variable (Y) in einer experimentellen Studie ausgewirkt hat.
• Mit anderen Worten, es wird untersucht, wie viel Varianz in Y auf X zurückzuführen ist.
• Sie können eine Effektgröße nur berechnen, nachdem Sie einen geeigneten statistischen Test auf Signifikanz durchgeführt haben.

Effektgröße | numerisch

model.tables(mod2, se = T)

Tables of effects

 season 
season
spring summer 
 0.368 -0.368 

 density 
density
      8      15      30      45 
 0.6532  0.2058 -0.2834 -0.5756 

Standard errors of effects
        season density
        0.1162  0.1644
replic.     12       6

Effektgröße | grafisch

plot.design(eggs ~ season, 
  data = sipho1)

plot.design(eggs ~ density, 
  data = sipho1)

Fragen..??

Total konfus?

Hilfreiche Buchkapitel zum Nachlesen

• Kapitel 11.2 - Factorial experiments in The R Book von M.J. Crawley.
• Kapitel 9.2 - Factorial designs in Experimental Design and Data Analysis for Biologists von G.P. Quinn & M.J. Keough

Übungsaufgabe

Übung

• Durchführung einer 2-faktoriellen ANOVA zu einem Fütterungsexperiment.
• Das R Notebook und der Datensatz sind im Moodlekurs (Woche 1) zu finden.

Total gelangweilt?

Dann testen Sie doch Ihr Wissen in folgendem Abschlussquiz…

Abschlussquiz

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de


Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.