# A tibble: 20 × 4
ek_id dosis_num dosis_fac zellzahl
<int> <dbl> <fct> <dbl>
1 1 0 0 39
2 2 0 0 45
3 3 0 0 81
4 4 0 0 51
5 5 0 0 53
6 6 0 0 84
7 7 0 0 59
8 8 0 0 25
9 9 0 0 36
10 10 0 0 41
11 11 100 100 104
12 12 100 100 87
13 13 100 100 88
14 14 100 100 82
15 15 100 100 69
16 16 100 100 116
17 17 100 100 90
18 18 100 100 41
19 19 100 100 94
20 20 100 100 71
12-Grundlagen des experimentellen Designs (Teil 2)
Data Science 2
Saskia Otto & Monika Eberhard
Universität Hamburg, IMF & IZS
Sommersemester 2025
Lernziele
Nach Abschluss dieser VL und Übung..
- haben Sie einen Eindruck, was das ideale Experiment ausmacht.
- kennen Sie die vier Hauptkomponenten, welche die Variabilität der Messgröße Y beeinflussen, und haben einen Eindruck, wie man diese besser kontrollieren kann.
- haben Sie einen Überblick über die gebräuchlichsten Designtypen in der Biologie.
- können Sie die die geeignete statistische Analyse beim sog. Completely Randomised Design (CRD) auswählen und in R durchführen.
Grundzüge des experimentellen Designs

Im Idealfall gilt,…
- Effekte können eindeutig und ohne Verzerrung geschätzt werden.
- die Schätzungen sind präzise.
- die Schätzungen sind vor möglichen einmaligen Ereignissen geschützt, die die Ergebnisse beeinträchtigen könnten.
- das Experiment ist leicht durchführbar.
- die Daten sind einfach zu analysieren und zu interpretieren.
- bei festem Zeit-, Ressourcen- und Stichprobenaufwand wird ein Maximum an Informationen gewonnen.
- die Ergebnisse sind auf eine Vielzahl von Personen, Bedingungen und Situationen anwendbar.
→ Dies kann nur durch eine sorgfältige Planung vorweg erreicht werden, nicht nachdem die Daten erhoben wurden.
Die grundlegende Gleichung der Versuchsplanung

Komponente 1 der Gleichung
Behandlungseffekte (‘treatment effect’)
- Werden durch die Manipulation und Eingriffe des Experimentators verursacht.
- Schlussfolgerungen über die Behandlungsstufen machen zu können, ist das Hauptziel des Experiments.
- Das Hauptaugenmerk bei der Versuchsplanung sollte hierauf liegen.
- Werden oft auch ‘Faktoren’ genannt und die einzelnen Kategorien die Faktorstufen
- Beispiele
- Präparat: ‘Zugabe’ vs. ‘keine Zugabe’
- Umwelt: ‘Standard’ vs. ‘Angereichert’
Komponente 2 der Gleichung
Biologische Effekte
- Unterschiede, die durch intrinsische Eigenschaften des Probenmaterials zustande kommen und nicht durch aktive Manipulation.
- Dies muss in der Versuchsplanung berücksichtigt werden: sollen Effekte explizit mit modelliert werden oder nicht?
- Beispiel Geschlecht → die Männchen vieler Arten sind schwerer als die Weibchen. Ist Y nun das Gewicht, wird ein Teil der Variabilität durch das Geschlecht verursacht. Mögliche Lösungen:
- Nur ein Geschlecht untersuchen, um diesen Effekt konstant zu halten.
- → Nachteil: Interpolation gefährlich
- Beide Geschlechter untersuchen, damit die Schlussfolgerungen über die Behandlung für beide gültig ist.
- → Vorteil: testbar, ob sich der Behandlungseffekt zwischen den Geschlechtern unterscheidet (sog. Interaktionseffekte).
- → Nachteil: Design meist komplexer und es werden noch mehr Parameter geschätzt bei einem fixen Stichprobenumfang, was zu ein Herabsenkung der Teststärke führt.
- Nur ein Geschlecht untersuchen, um diesen Effekt konstant zu halten.
Komponente 3 der Gleichung
Technische Effekte
- Beziehen sich auf die Eigenschaften der Versuchsanlage.
- Alle möglichen Effekte sollten im Vorfeld identifiziert werden und dann konstant gehalten werden.
- Beispiel DNA-Mikroarray Studien → Proben werden über mehrere Tage hybridisiert und gescannt, was einen Tageseffekt einführt. Mögliche Lösungen:
- Alle Proben an einem Tag analysieren.
- Unterproben (gleiches N) aus allen Faktorstufen am gleichen Tag analysieren
Komponente 4 der Gleichung
4 Typen von Fehlern
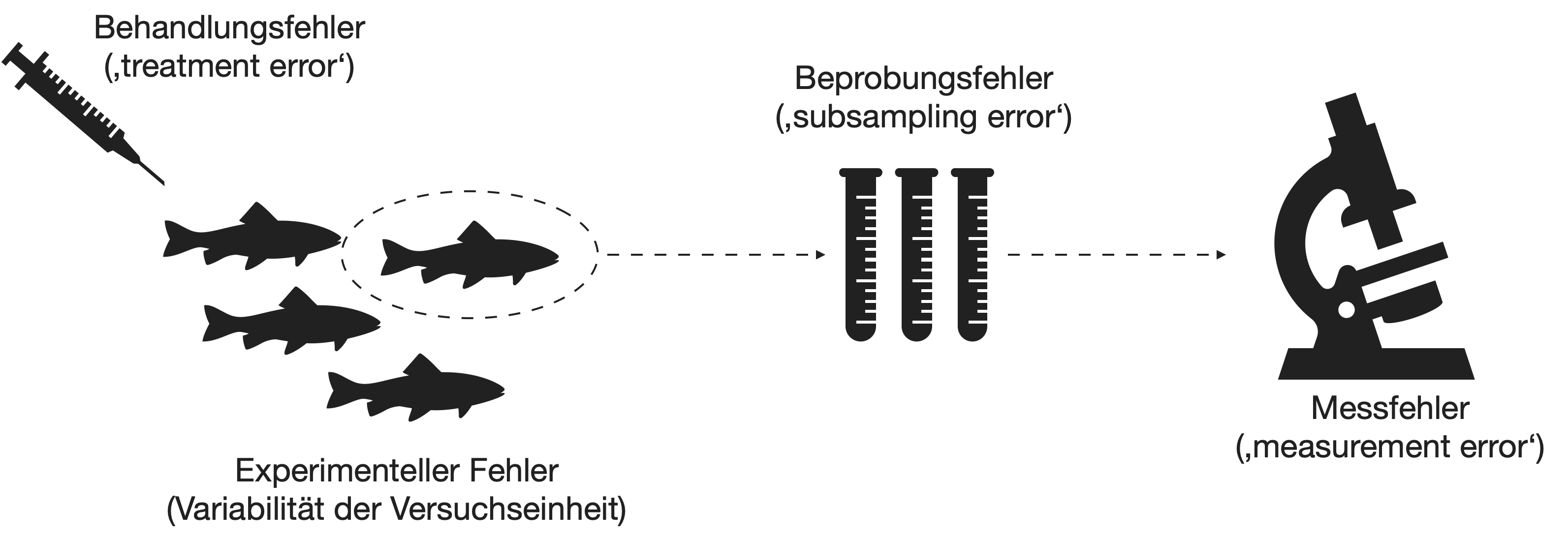
Komponente 4 der Gleichung | 4 Typen
Behandlungsfehler (‘treatment error’)
- Exakte Replikation der Behandlung nicht möglich.
- Beispiel: Es wird jedes Mal eine unterschiedliche Menge eines Präparats injiziert oder in unterschiedliche Körperstellen.
- Vermeidbar durch Standardisierung; verbessert sich mit der Erfahrung der/des WissenschaftlerIn.
Experimenteller Fehler (‘experimental error’)
- Die natürliche Streuung der experimentellen Einheiten (z.B. der Fische).
- Schwer vom Behandlungsfehler zu unterscheiden.
- Oft sehr groß bei Menschen, kleiner bei kleinen Tieren und noch kleiner bei in vitro Studien.
Beprobungsfehler (‘sampling error’)
- Stichprobe und Unterproben nicht repräsentativ.
- In der experimentellen Biologie gibt es häufig Probenteilungen und somit auch die Gefahr der ungenauen Teilung bzw. Unterprobenahme.
- → Fehlerrate reduzierbar durch Erhöhung der Unterprobenzahl.
Messfehler (‘measurement error’)
- Unpräzise Messgeräte.
- Schwierigkeit im Handling
- Unklare Definition, was genau gemessen werden soll.
- Können allerdings leicht quantifiziert werden, indem wiederholte Messungen an der gleichen Probe genommen werden.
Häufige Designtypen
und entsprechende (parametrische) Analysen
Vollständig randomisiertes Design - Completely Randomised Design (CRD)
- Alle Versuchseinheiten sind unabhängig und werden den Kombinationen an Behandlungsstufen zufällig zugeordnet.
- Unterscheidet in
- 1 Faktor, 2 Gruppen → t-Test (oder 1-way ANOVA)
- 1 Faktor, mehrere Gruppen → 1-way ANOVA (oder Regression )
- 2 Faktoren, gekreuzt → 2-way crossed ANOVA
- 1 Faktor mit Unterproben (Pseudoreplikation) → 2-way nested ANOVA
- 1 Faktor, 1 Kovariate → ANCOVA
Weitere Designs
- Randomisiertes Blockdesign (RBD)
- Design mit Messwiederholung (Repeated measures design - RM)
- Split-Plot-Design
Completely Randomised Design (CRD)
Completely Randomised Design (CRD)
Alle experimentellen Einheiten sind unabhängig und können zufällig allen Kombinationen von Behandlungsstufen zugeteilt werden.
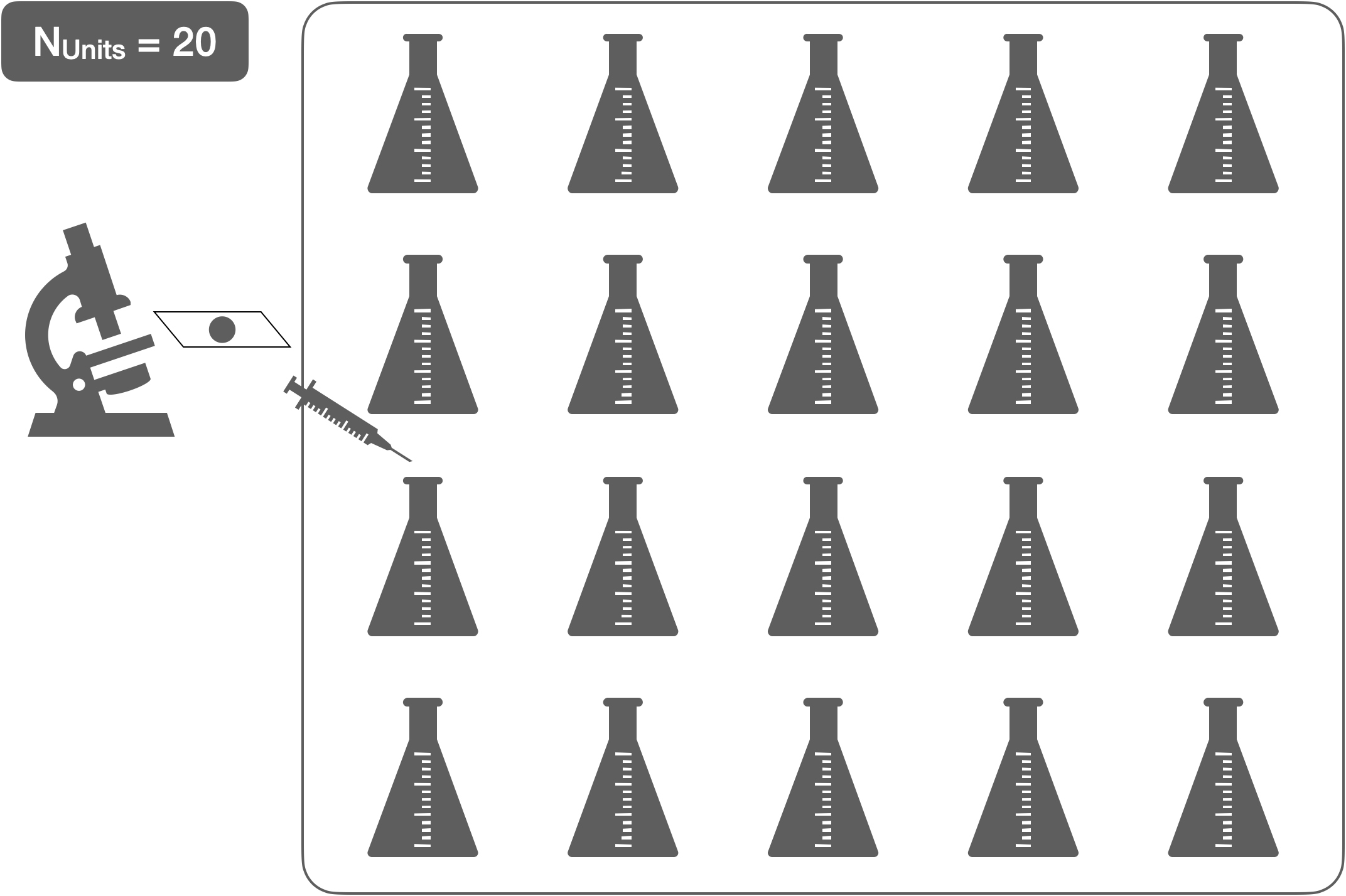
CRD - 1 Faktor (2 Gruppen)
Design
- N: 20 (Exp. Units: Erlenmeyerkolben)
- n: 10 (EK pro Dosis)
- Ergebnis: Zellzahl
- Behandlungseffekt: Dosis (fest) = {0, 100}
- Analyse: t-Test (oder 1-way ANOVA)
- Freiheitsgrade:
\begin{align*} \text{Ergebnis} &= \text{Dosis} + \text{Fehler}\\ \text{(N - 1)} &= \text{(p - 1)} + \text{(N - p)}\\ \text{(19)} &= \text{(1)} + \text{(18)} \end{align*}
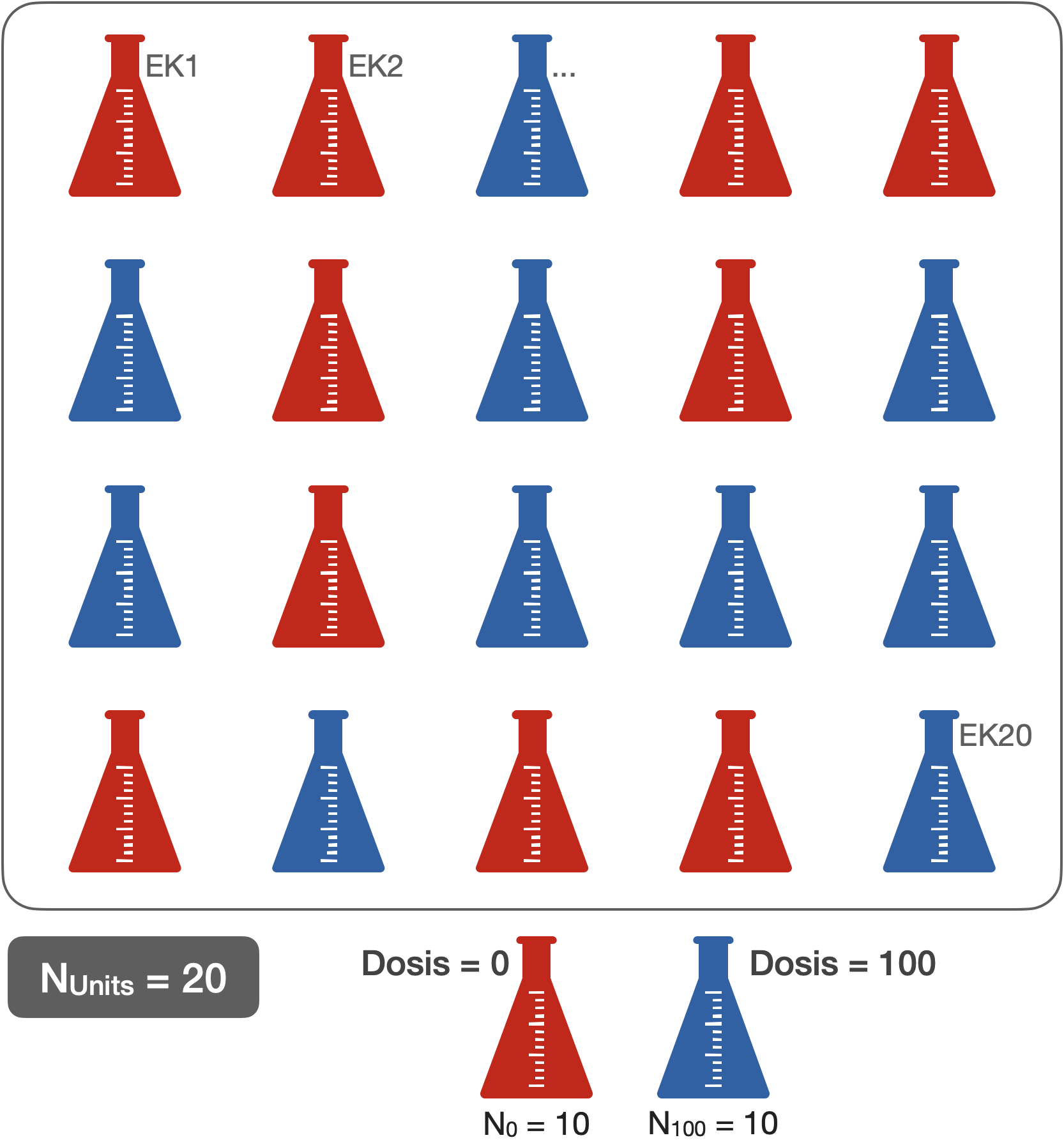
CRD - 1 Faktor (2 Gruppen) | Beispieldaten
CRD - 1 Faktor (2 Gruppen) | Beispielcode 1
![]()
Two Sample t-test
data: zellzahl by dosis_fac
t = -4, df = 18, p-value = 0.002
alternative hypothesis: true difference in means between group 0 and group 100 is not equal to 0
95 percent confidence interval:
-51.4 -14.2
sample estimates:
mean in group 0 mean in group 100
51.4 84.2 Df Sum Sq Mean Sq F value Pr(>F)
dosis_fac 1 5379 5379 13.7 0.0016 **
Residuals 18 7068 393
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1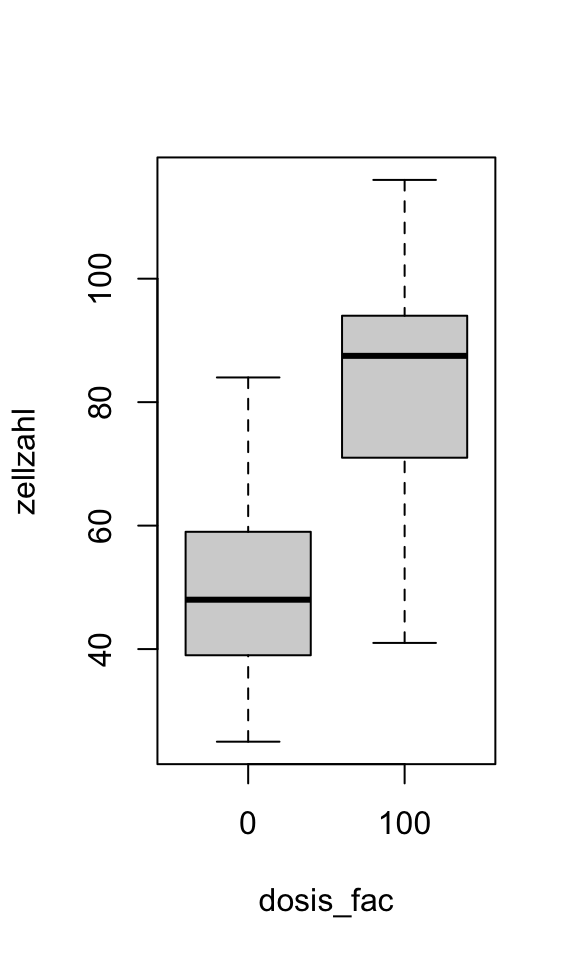
CRD - 1 Faktor (2 Gruppen) | Beispielcode 2
![]()
Richtiges Ergebnis trotz falschem Datentyp
Two Sample t-test
data: zellzahl by dosis_num
t = -4, df = 18, p-value = 0.002
alternative hypothesis: true difference in means between group 0 and group 100 is not equal to 0
95 percent confidence interval:
-51.4 -14.2
sample estimates:
mean in group 0 mean in group 100
51.4 84.2 Df Sum Sq Mean Sq F value Pr(>F)
dosis_num 1 5379 5379 13.7 0.0016 **
Residuals 18 7068 393
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1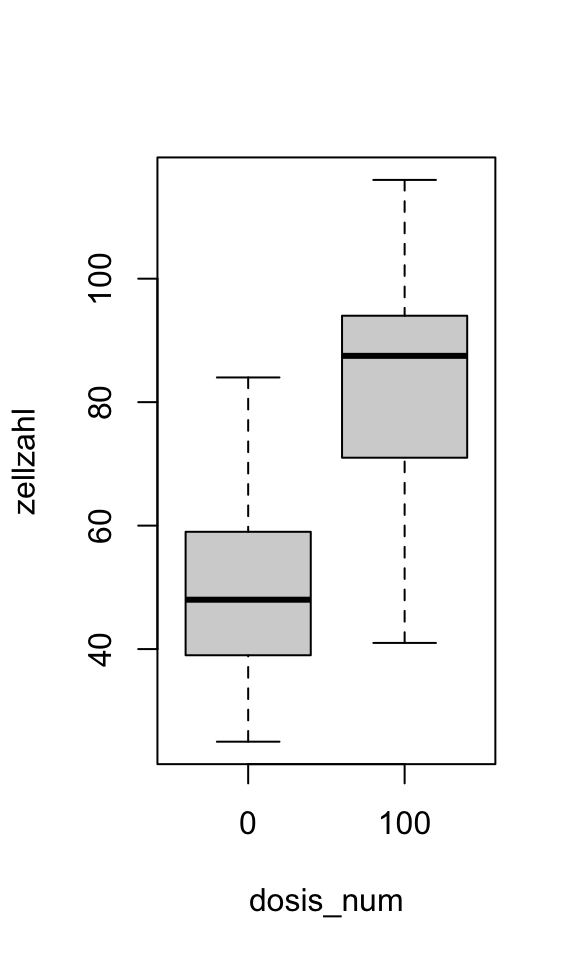
CRD - 1 Faktor (4 Gruppen)
Design
- N: 20 (Exp. Units: Erlenmeyerkolben)
- n: 5 (EK pro Dosis)
- Ergebnis: Zellzahl
- Behandlungseffekt: Dosis (fest) = {0,50,100,150}
- Analyse: 1-way ANOVA (oder Regression)
- Freiheitsgrade:
Dosis ist kategorial (ANOVA): \begin{align*} \text{Ergebnis} &= \text{Dosis} + \text{Fehler}\\ \text{(N - 1)} &= \text{(p - 1)} + (\text{N - p})\\ \text{(19)} &= \text{(3)} + (\text{16}) \end{align*}
Dosis ist kontinuierlich (Regression): \begin{align*} \text{Ergebnis} &= \text{Dosis} + \text{Fehler}\\ \text{(19)} &= \text{(1)} + (\text{18}) \end{align*}

CRD - 1 Faktor (4 Gruppen) | ANOVA Tabelle
Typische Tabelle einer 1-faktoriellen Varianzanalyse

CRD - 1 Faktor (4 Gruppen) | Beispieldaten
# A tibble: 20 × 4
ek_id dosis_num dosis_fac zellzahl
<int> <dbl> <fct> <dbl>
1 1 0 0 39
2 2 0 0 45
3 3 0 0 81
4 4 0 0 51
5 5 0 0 53
6 6 50 50 114
7 7 50 50 89
8 8 50 50 55
9 9 50 50 66
10 10 50 50 71
11 11 100 100 124
12 12 100 100 107
13 13 100 100 108
14 14 100 100 102
15 15 100 100 89
16 16 150 150 141
17 17 150 150 115
18 18 150 150 66
19 19 150 150 119
20 20 150 150 96CRD - 1 Faktor (4 Gruppen) | 1-way ANOVA
Df Sum Sq Mean Sq F value Pr(>F)
dosis_fac 3 9713 3238 7.42 0.0025 **
Residuals 16 6978 436
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1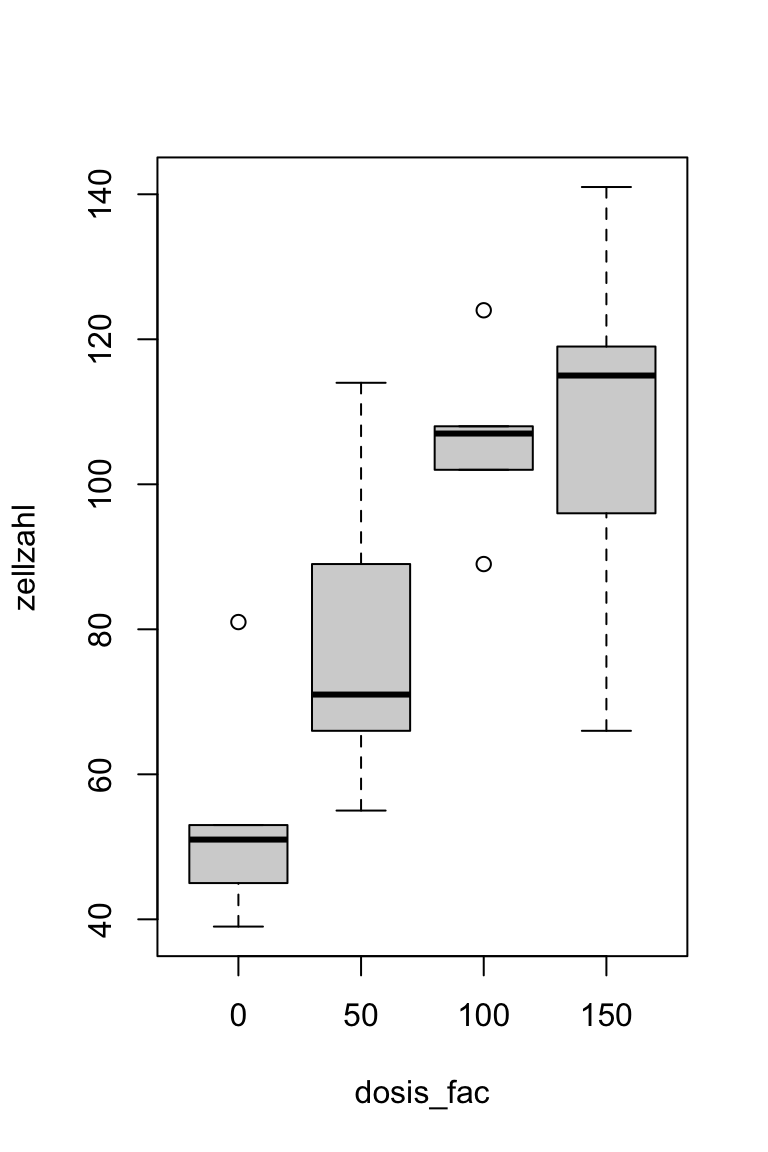
![]()
![]()
CRD - 1 Faktor (4 Gruppen) | Regression 1
![]()
Call:
lm(formula = zellzahl ~ dosis_num, data = df)
Residuals:
Min 1Q Median 3Q Max
-48.72 -11.71 -2.55 11.90 36.84
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 58.3800 7.8256 7.46 6.5e-07 ***
dosis_num 0.3756 0.0837 4.49 0.00028 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 20.9 on 18 degrees of freedom
Multiple R-squared: 0.528, Adjusted R-squared: 0.502
F-statistic: 20.2 on 1 and 18 DF, p-value: 0.000283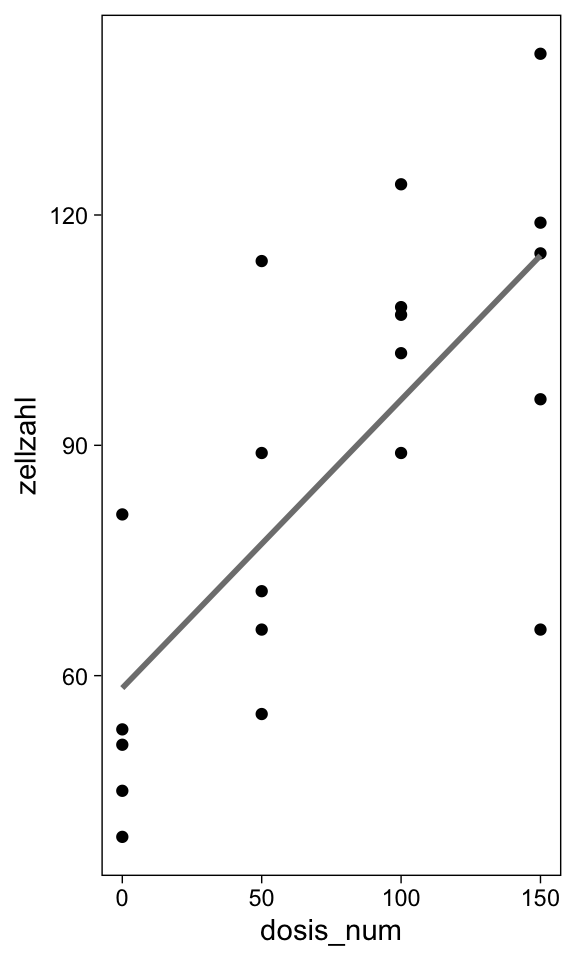
CRD - 1 Faktor (4 Gruppen) | Regression 2
![]()
Call:
lm(formula = zellzahl ~ dosis_fac, data = df)
Residuals:
Min 1Q Median 3Q Max
-41.4 -11.8 -1.8 10.4 35.0
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 53.80 9.34 5.76 0.000029 ***
dosis_fac50 25.20 13.21 1.91 0.07451 .
dosis_fac100 52.20 13.21 3.95 0.00114 **
dosis_fac150 53.60 13.21 4.06 0.00091 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 20.9 on 16 degrees of freedom
Multiple R-squared: 0.582, Adjusted R-squared: 0.504
F-statistic: 7.42 on 3 and 16 DF, p-value: 0.00247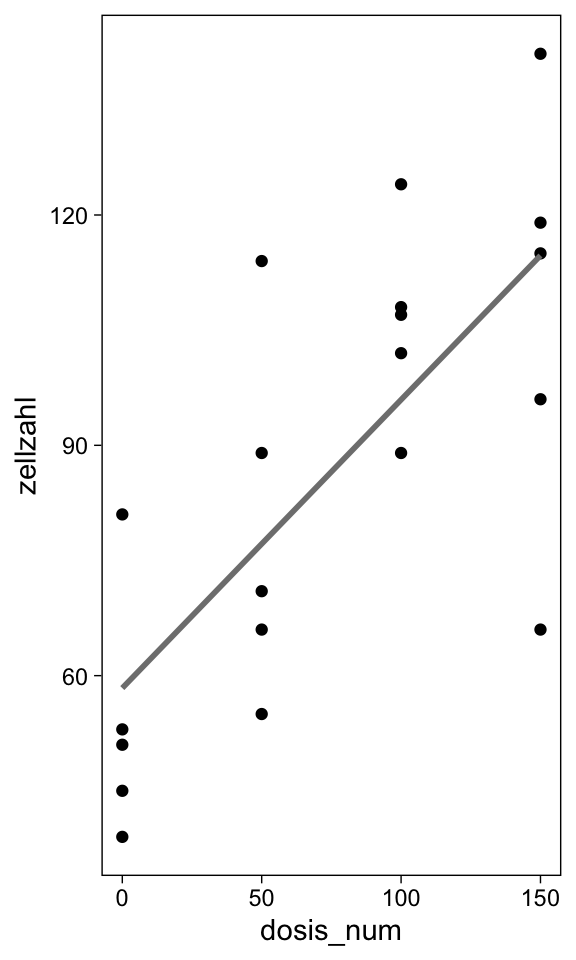
Passende Analyse zum Design
ANOVA oder besser Regression?
- Wenn der Behandungseffekt (Faktor) eigentlich eine stetige Variable mit nur wenigen Werten repräsentiert, sollte dann eine ANOVA oder eine Regression durchgeführt werden?
Beispiel: Effekte eines Anti-Depressivums bei Nagetieren
- 20 Ratten wird eine von 4 verschiedenen Dosen des Anti-Depressivums Fluoxetine gegeben (0, 60, 160 und 240 mg/l).
- Die gemessene Antwortvariable ist die totale Immobilitätszeit im Schwimmtest.
- Depressive Phänotypen weisen eine grundlegend höhere Zeit auf. Das Anti-Depressivum reduziert hingegen die totale Immobilitätszeit.
ANOVA oder besser Regression? | Design
Zusammenfassung des Designs
- Daten:
fluoxetineim labstats Paket - N: 20
- Ergebnis Y: totale Immobilitätszeit im Schwimmtest (
time.immob) - Behandlungseffekte: Dosis (fest) = {0, 80, 160, 240}
- Dosis kann als kategoriale und stetige Variable behandelt werden:

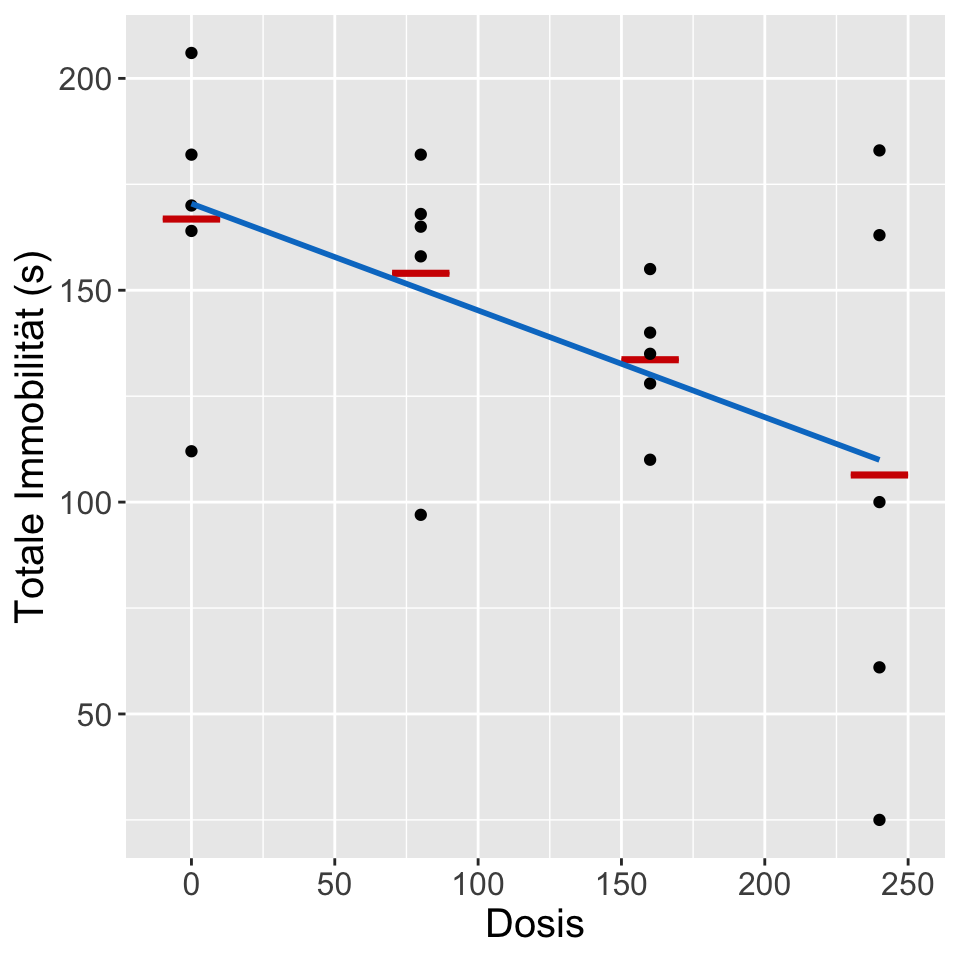
ANOVA oder besser Regression? | Analyse 1
Vergleich FG und p
![]()
![]()
![]()
ANOVA oder besser Regression? | Analyse 2
Vergleich FG und p
Call:
lm(formula = time.immob ~ dose, data = fluoxetine)
Residuals:
Min 1Q Median 3Q Max
-85.0 -12.5 6.3 19.5 73.0
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 170.4400 14.8368 11.49 1e-09 ***
dose -0.2520 0.0991 -2.54 0.02 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 39.7 on 18 degrees of freedom
Multiple R-squared: 0.264, Adjusted R-squared: 0.223
F-statistic: 6.46 on 1 and 18 DF, p-value: 0.0204![]()
![]()
ANOVA oder besser Regression? | Erklärung 1
Warum Differenzen im p-Wert?
- Der große Unterschied sind die Freiheitsgrade:
- Eine einfache Regression schätzt nur 2 Parameter (Achsenabschnitt und Steigung, df = 2-1), während die ANOVA hier 4 schätzen muss (die Gruppenmittelwerte, df = 4-1)
- Grundsätzlich passt sich ein Modell mit mehr Parametern besser an die Daten an. Aber es ist auch komplexer und kann damit an Teststärke verlieren.
ANOVA oder besser Regression? | Erklärung 2
Weitere Vorteile der Regression
- Das ANOVA Modell betrachtet nur die Unterschiede in Gruppenmittelwerten, also ob es eine Abweichung von Null geht. R weiß nicht, dass die 4 Kategorien eine Reihenfolge haben und kann daher diese Information nicht nutzen.
- Wenn es aber um ein bestimmtes Muster geht, wie um eine Dosis-Wirkungs-Beziehungen, ist ein fokussierter Hypothesentest für diese spezifische Beziehung oft teststärker als eine allgemeine ANOVA, die auf alle möglichen Beziehungen testet.
- Die Regression kann biologisch verwendbarere Ergebnisse produzieren als die ANOVA und ist daher tendenziell vorzuziehen.
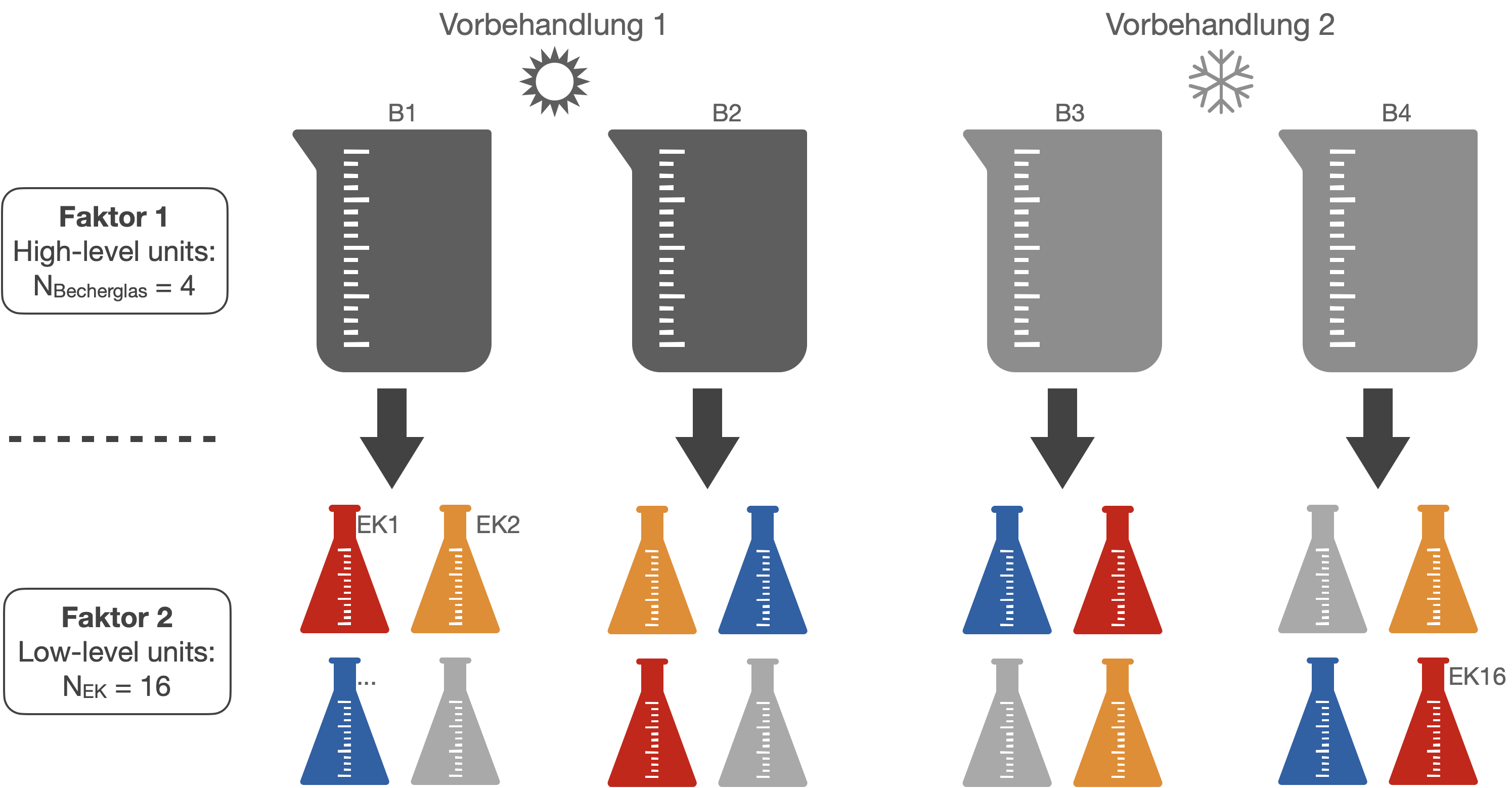
CRD - 2 gekreuzte Faktoren (je 2 Gruppen)
Gekreuztes Design
- N: 20 (Erlenmeyerkolben)
- n: 5 (EK pro Dosis/Typ)
- Ergebnis: Zellzahl
- Behandlungseffekte:
- Dosis (fest) = {0, 100}
- Typ (fest) = {1, 2}
- Dosis (fest) = {0, 100}
- Analyse: 2-way crossed/factorial ANOVA

CRD - 1 Faktor (2 Gruppen) mit Unterprobe
Verschachteltes Design
- N: 8 (Exp. Units: Erlenmeyerkolben)
- n: 3 (Objektträger als Unterproben pro EK)
- Ergebnis: Zellzahl
- Effekte:
- Behandlungseff.: Dosis (fest) = {0, 100}
- Technischer Eff.: EK (zufällig) = {1,2,3,..,8}
- Analyse: 2-way nested ANOVA (oder ‘summary measure’ analysis)
- Freiheitsgrade:
\begin{align*} \text{Ergebnis} &= \text{Dosis} + \text{Fehler}\\ \text{(N - 1)} &= \text{(p - 1)} + \text{(N - p)}\\ \text{(7)} &= \text{(1)} + \text{(6)} \end{align*}
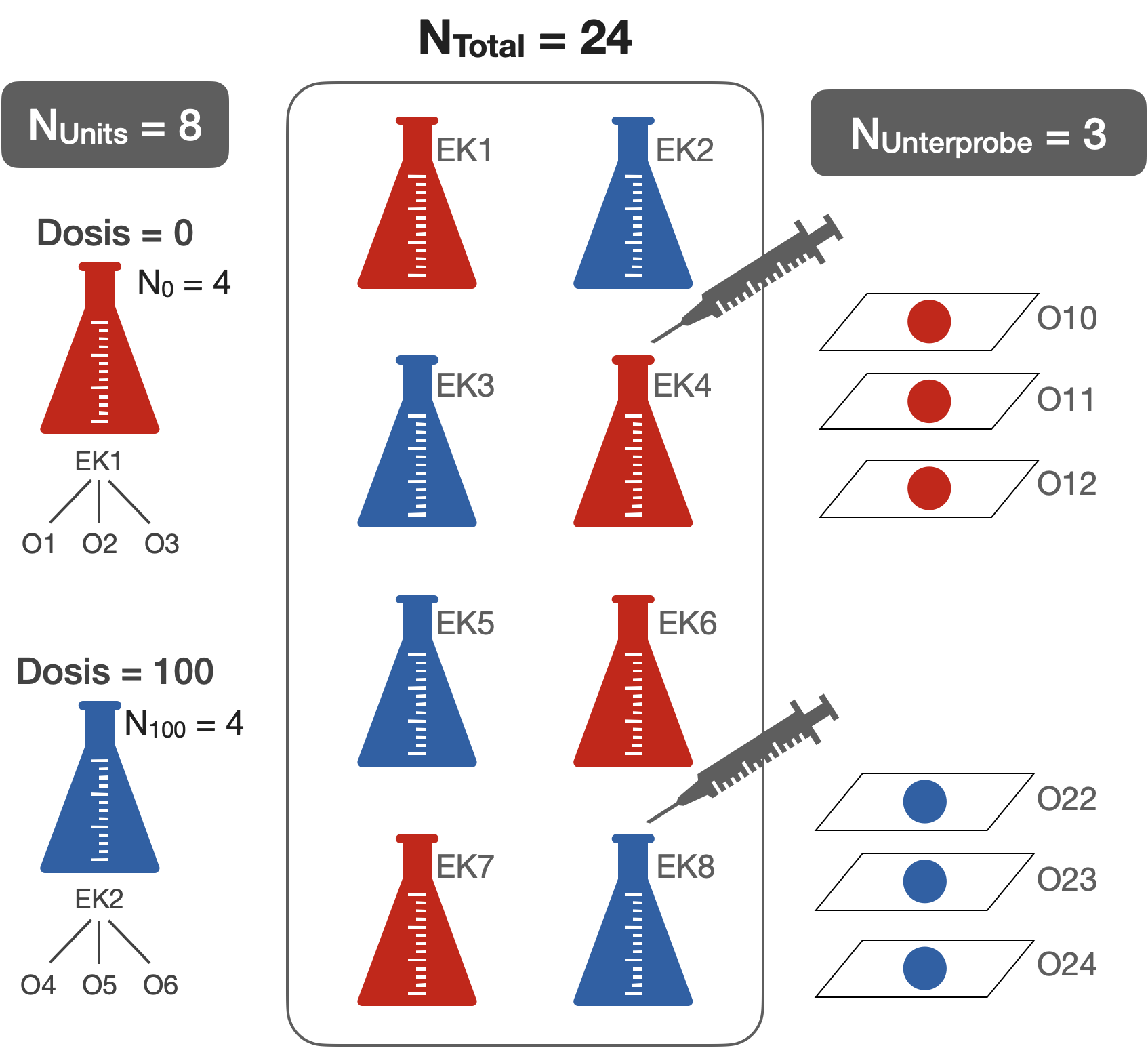
CRD - 1 Faktor mit Unterprobe | Beispieldaten
# A tibble: 24 × 5
obj_id ek_id_fac dosis_fac ef_falsch_codiert zellzahl
<int> <fct> <fct> <fct> <dbl>
1 1 1 0 1 63
2 2 1 0 1 56
3 3 1 0 1 48
4 4 2 0 2 55
5 5 2 0 2 56
6 6 2 0 2 64
7 7 3 0 3 55
8 8 3 0 3 55
9 9 3 0 3 54
10 10 4 0 4 39
11 11 4 0 4 51
12 12 4 0 4 44
13 13 5 100 1 79
14 14 5 100 1 93
15 15 5 100 1 87
16 16 6 100 2 92
17 17 6 100 2 96
18 18 6 100 2 92
# ℹ 6 more rowsCRD - 1 Faktor mit Unterprobe | Ansätze
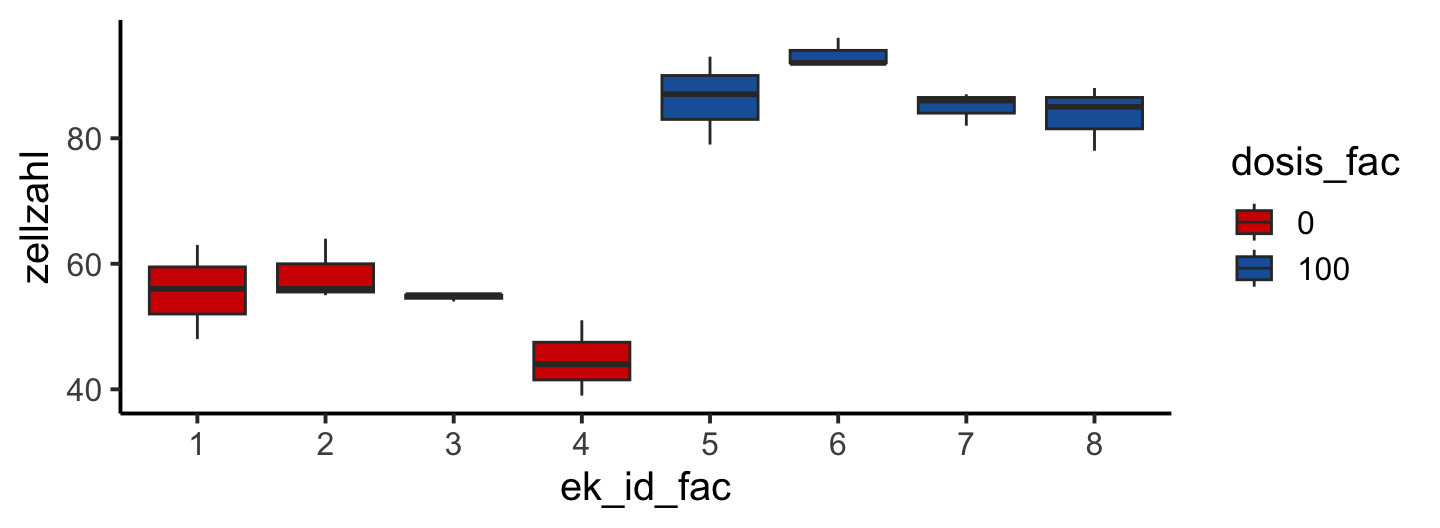
- Falscher Ansatz:
- 1-faktorielle ANOVA, ohne Berücksichtigung der Pseudoreplikation
- Richtige Ansätze:
- 1-faktorielle ANOVA mit gemittelten Unterprobewerte (‘summary measure’ analysis).
- 2-faktorielle ANOVA, genestetes Design: mit der
Error()Funktion innerhalb deraov()Formel. - Lineares gemischtes Modell (LME) mit dem R Paket nlme oder lme4.
CRD - 1 Faktor mit Unterprobe | Falscher Ansatz
![]()
Df Sum Sq Mean Sq F value Pr(>F)
dosis_fac 1 6834 6834 167 9.4e-12 ***
Residuals 22 900 41
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- Die Freiheitsgerade der Residuen betragen hier 22!
- Die FG zur Berechnung des F- und p-Werts der Behandlungsvariable (Dosis) dürfen nicht höher sein als die experimentellen Einheiten selbst (hier 8).
- Dadurch ist der F-Wert viel höher und der p-Wert viel niedriger als korrekt wäre.
CRD - 1 Faktor mit Unterprobe | Ansatz 1
![]()
1-faktorielle ANOVA mit gemittelten Unterprobewerten
Df Sum Sq Mean Sq F value Pr(>F)
dosis_fac 1 2278 2278 83.9 0.000095 ***
Residuals 6 163 27
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- Hier wird das Problem der Pseudoreplikation durch die Mittelwertbildung gelöst.
CRD - 1 Faktor mit Unterprobe | Ansatz 2
![]()
2-faktorielle ANOVA, genestetes Design: Error() in aov()
Error: ek_id_fac
Df Sum Sq Mean Sq F value Pr(>F)
dosis_fac 1 6834 6834 83.9 0.000095 ***
Residuals 6 489 81
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Error: Within
Df Sum Sq Mean Sq F value Pr(>F)
Residuals 16 411 25.7 - Wenn das Design ausbalanciert ist, dann entspricht das Ergebnis der oberen ANOVA Tabelle dem der ‘summary measure’ ANOVA.
CRD - 1 Faktor mit Unterprobe | Ansatz 2
![]()
Wenn die ID der Erlenmeyerkolben nicht einmalig ist
Error: ef_falsch_codiert
Df Sum Sq Mean Sq F value Pr(>F)
Residuals 3 413 138
Error: Within
Df Sum Sq Mean Sq F value Pr(>F)
dosis_fac 1 6834 6834 267 1.2e-12 ***
Residuals 19 486 26
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Konsequenzen falscher Kodierung
- Hier denkt R, dass das Design für Dosis und Proben gekreuzt und nicht genestet ist.
- Der Behandlungseffekt ist jetzt in die untere
Error: WithinANOVA Tabelle gerutscht und hier sind auch wieder die Freiheitsgrade zu hoch, was zu einem verfälschten F- und p-Wert führt!
CRD - 1 Faktor mit Unterprobe | Ansatz 3 mit dem nlme Paket
![]()
2-faktorielle ANOVA, genestetes Design: random Argument in lme()
numDF denDF F-value p-value
(Intercept) 1 16 1452 <.0001
dosis_fac 1 6 84 0.0001- Sogenannte ‘mixed-effects models’ (gemischte, hierarchische oder multi-level Modelle genannt) sind komplexer und haben mehr Annahmen, z.B. dass die Verteilung des zufälligen Faktors normal ist.
- Standardwerk für diese Modelle ist Mixed-Effects Models in S and S-Plus von Pinheiro und Bates.
- Eine gute und kurze Einführung gibt es auch in The R Book von Micheal J. Crawley
- Nützliche R Pakete sind nlme and lme4.
CRD - Komplexe verschachtelte Designs
Beispiel: Räumliche Variabilität von Blattlausdichten
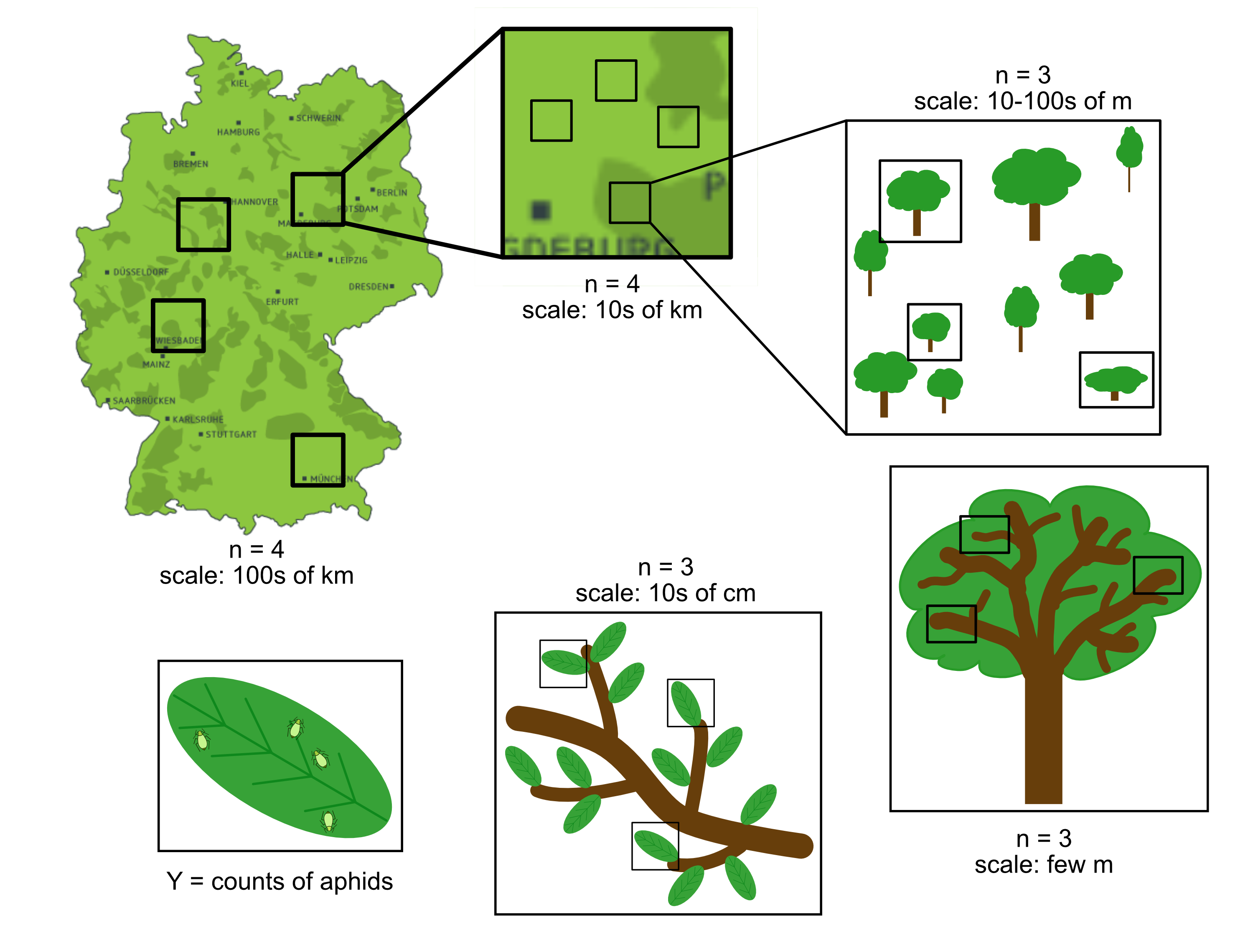
- Gerade bei räumlichen und zeitlichen Feldstudien ist das Beprobungsdesign oft stark verschachtelt.
- → Der größte Beprobungsaufwand sollte auf der Skala mit der höchsten Varianz erfolgen (viele Wiederholungen)!
Designtypen und geeignete Analysen - BRD, RM, Split-Plot Design

Randomised Block Design (RBD) | 1
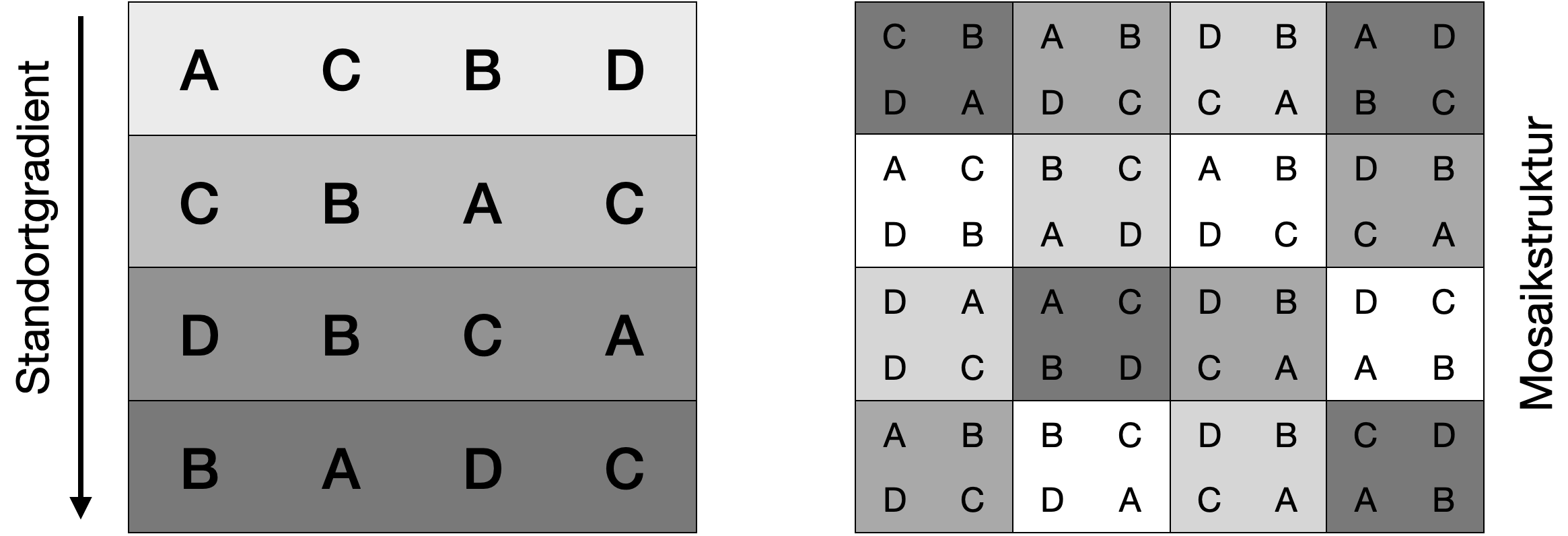
- Versuchseinheiten, die ähnliche Hintergrundbedingungen aufweisen, werden in ‘Blöcken’ gruppiert.
- Dadurch kann ein Teil der Gesamtvariation in der Antwortvariablen durch Unterschiede zwischen den Blöcken erklärt und somit die (unerklärte) Restvariabilität verringert werden.
Randomised Block Design (RBD) | 2

- Experimentelle Einheiten werden den Behandlungsstufen innerhalb eines Blocks zufällig zugeordnet.
- Anzahl an Kombinationsmöglichkeiten eingeschränkt.
- Im Idealfall sind alle Behandlungsstufen in allen Blöcken zu gleichen Anteilen vertreten.
Repeated Measures (RM) Design | 1
- Auch Längsschnittstudie oder Longitudinalstudie genannt.
- Hier werden mehrere Messungen mit der gleichen experimentellen Einheit über die Zeit gemacht → diese sind daher zeitlich voneinander abhängig!

Repeated Measures (RM) Design | 2
Mögliche Fragestellungen
- Veränderungen über die Zeit?
- Gesamtunterschied zwischen den Behandlungsgruppen?
- Gruppenunterschiede in der zeitlichen Entwicklung (sozusagen die Gruppe x Zeit Interaktion)?
Allgemeine Analyseansätze
- ‘Summary measure’ analysis → dafür braucht es aber Replikate!
- RM-ANOVA
- Lineare gemischte Modelle (Linear Mixed Effects Models - LME)
Split-Plot Design | 1
- Split-Unit- oder Split-Plot-Versuche wurden ursprünglich in der Landwirtschaft durchgeführt.
- Sie stellen ein randomisiertes Blockdesign (RBD) dar:
- Ein Faktor (oder eine Reihe von Faktoren) wird auf ganze Blöcke angewendet, mit Wiederholungsblöcken für jede Stufe dieses Faktors.
- Ein oder mehrere Faktoren werden dann auf die Versuchseinheiten innerhalb jedes Blocks angewendet werden.
- Ein Faktor (oder eine Reihe von Faktoren) wird auf ganze Blöcke angewendet, mit Wiederholungsblöcken für jede Stufe dieses Faktors.
- Das hierarchische Design führt zu experimentellen Einheiten auf verschiedenen Ebenen.
Split-Plot Design | 2
Übungsaufgaben
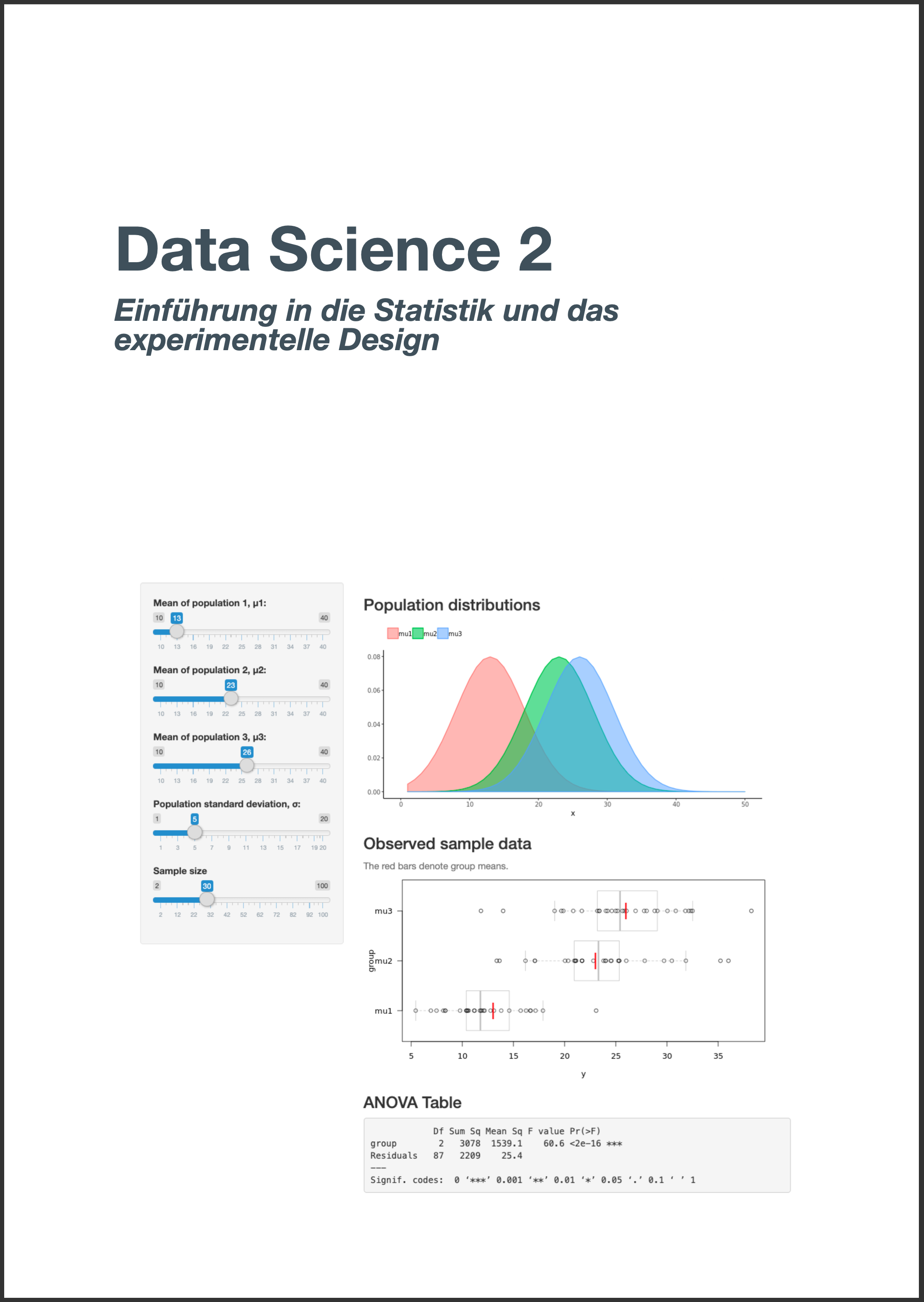
![]()
Übungstag 6
Poweranalyse und experimentelles Design
![]()
- Aufgaben:
- 6.1 Poweranalyse und Bestimmung des Stichprobenumfangs
- 6.2 Nachbereitung Fallstudie: Frage 4 und 5 - Bestimmung des Stichprobenumfang und Evaluation des experimentellen Designs und der Analyse
- R Notebook-Skript:
- DS2_06_UebungenPoweranalyse_expDesign_Fallstudie.Rmd
Fragen?
Abschlussquiz
![]()

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de

Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.
Kurswebseite: Data Science 2