11-Grundlagen des experimentellen Designs (Teil 1)

Data Science 2

Saskia Otto

Universität Hamburg, IMF

Sommersemester 2024

Lernziele

Nach Abschluss dieser VL und Übung..

  • kennen Sie einige der wichtigsten Kriterien die in die Versuchsplanung mit einfließen.
  • wissen Sie, was die Power, Teststärke oder Trennschärfe eines Tests ist und welche Faktoren eine Rolle spielen.
  • können Sie anhand der Poweranalyse die Teststärke, den optimalen Stichprobenumfang sowie den minimalen nachweisbaren Effekt beim Zwei- oder Mehr-Stichprobentest in R durchführen.
  • haben Sie einen Überblick über nützliche R Funktionen und Pakete für weitere statistische Verfahren

Wichtige Kriterien der Versuchsplanung

Einige Kriterien im einzelnen

Repräsentativität der Stichprobe


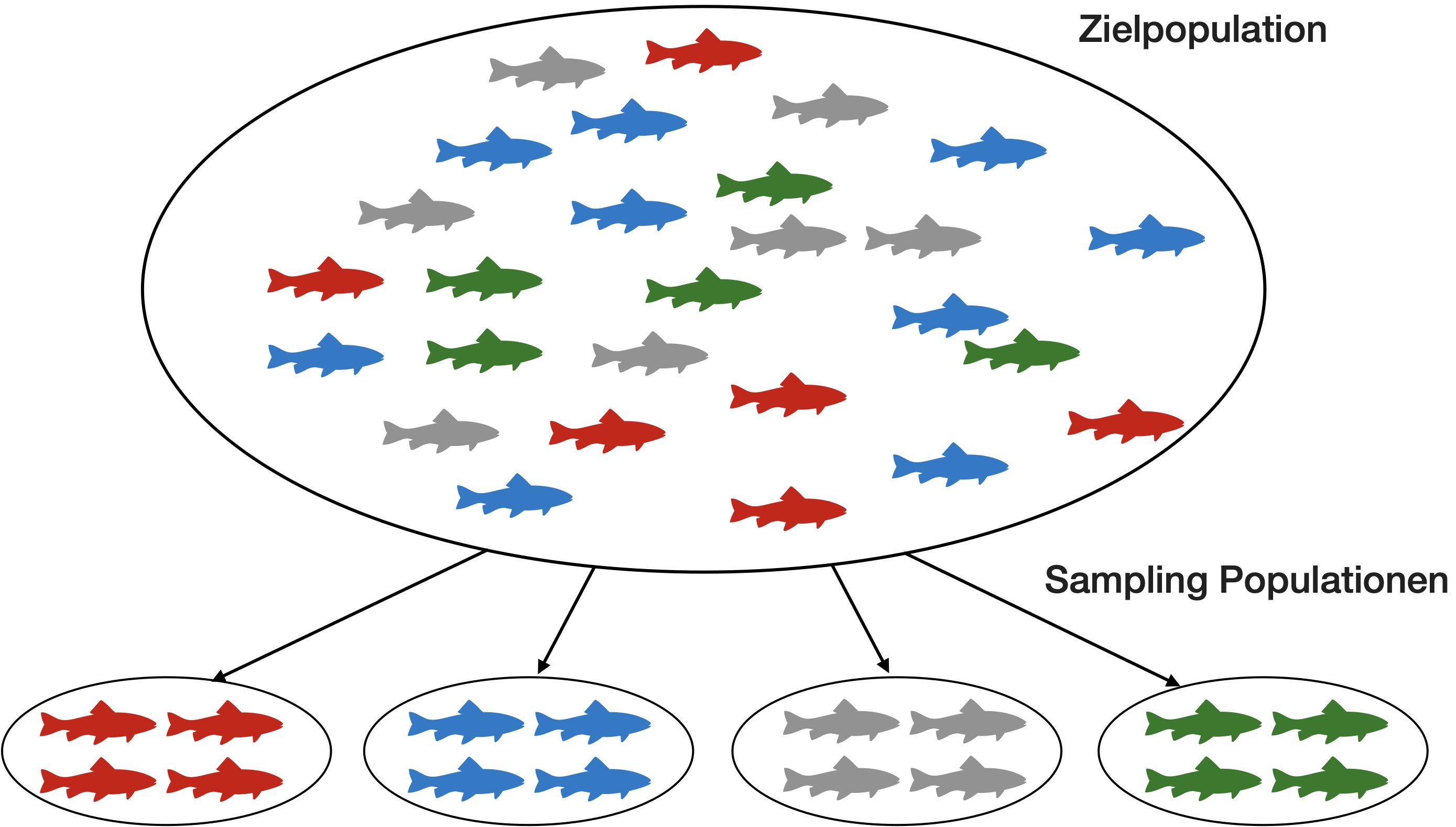
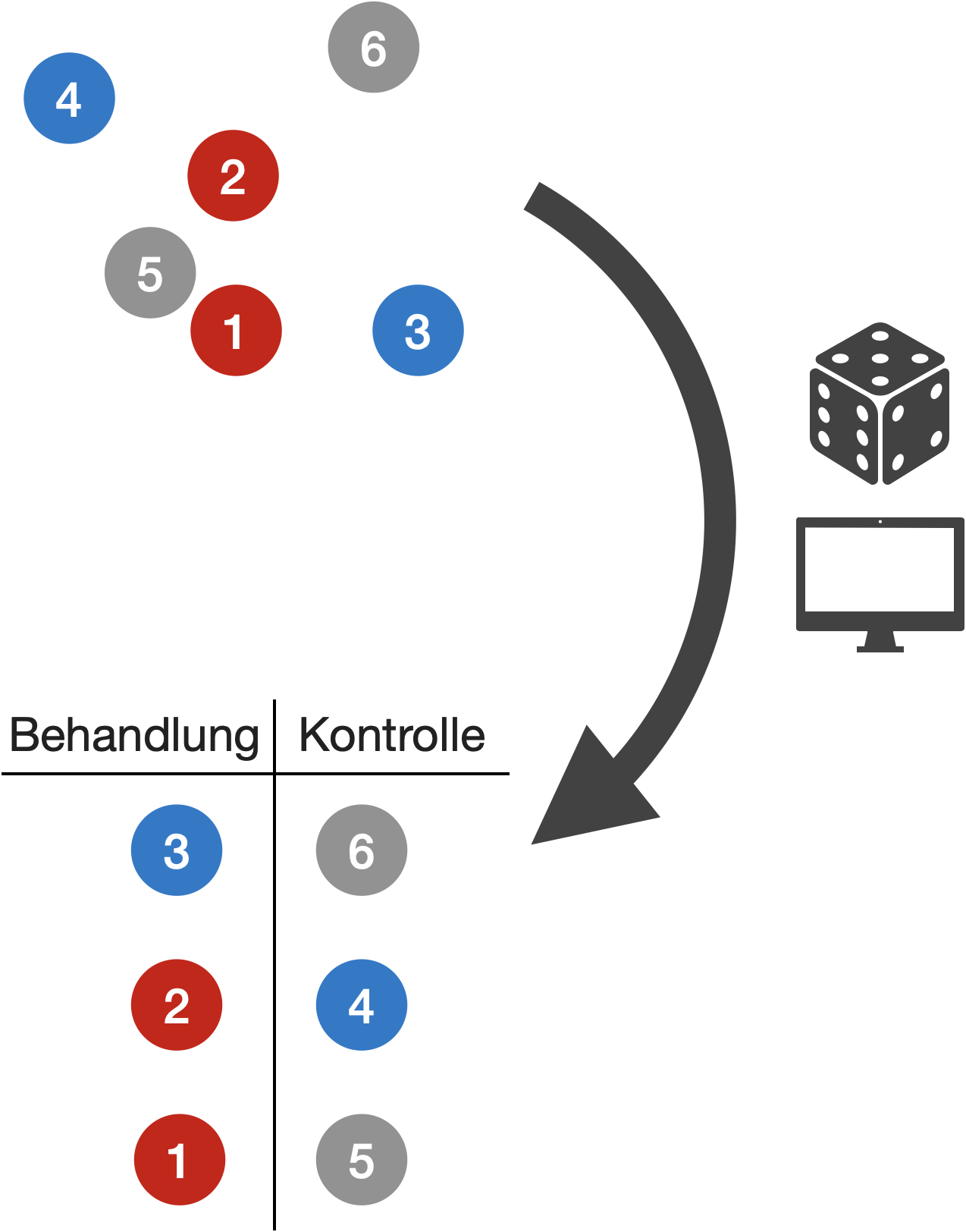
Randomisierung - der goldene Standard

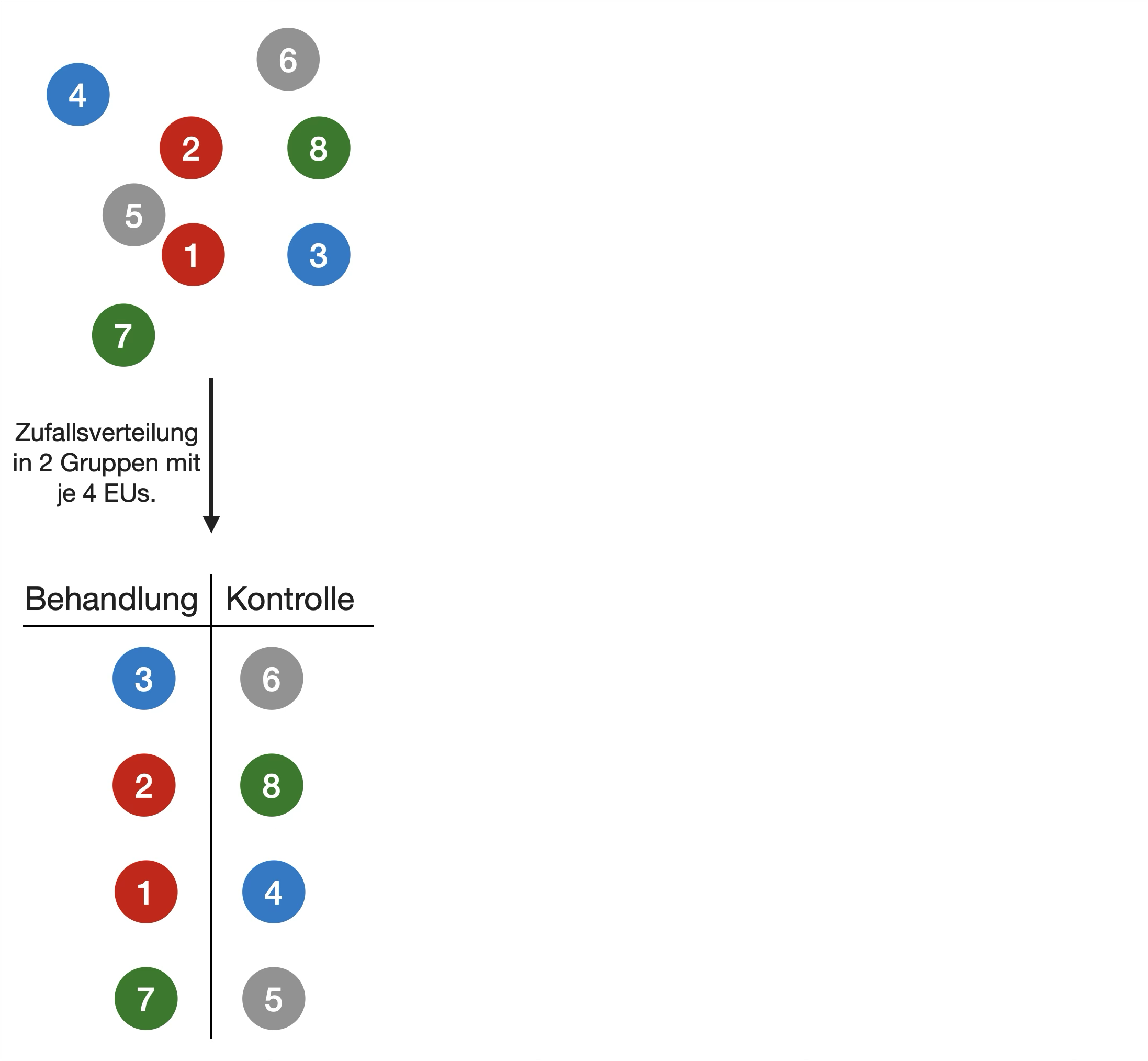
Blocking

  • Wenn Variation zwischen den EUs (experimentelle Fehler ) groß ist → Behandlungsfehler schwer zu erkennen
  • Ursachen für Variabilität:
    • EUs sind heterogen
    • EU bilden erkennbare Untergruppen (z. B. Männchen und Weibchen)
    • EUs werden in Chargen gruppiert, um das Experimentverfahren zu vereinfachen → diese technischen Artefakte beeinflussen das Ergebnis

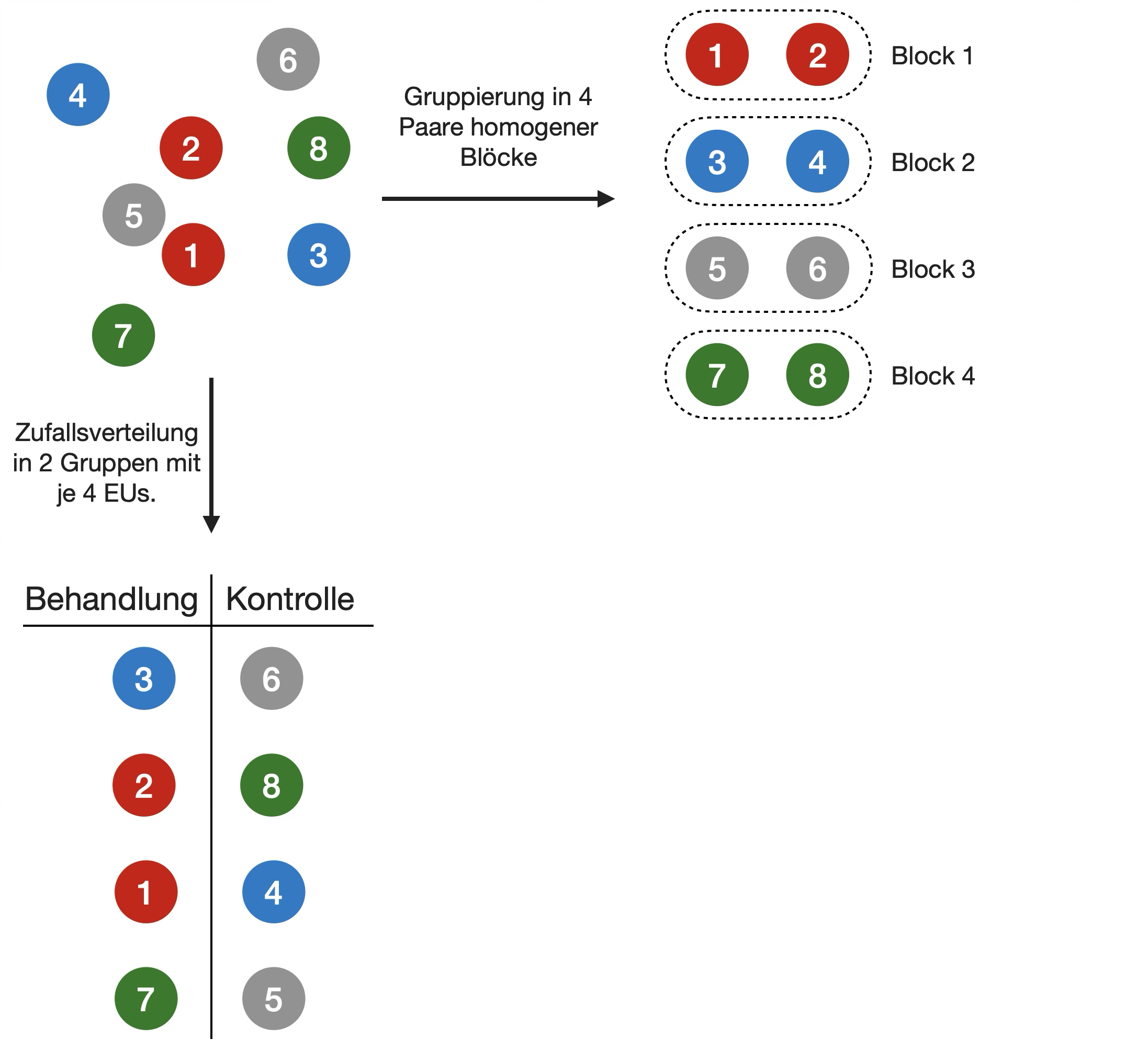
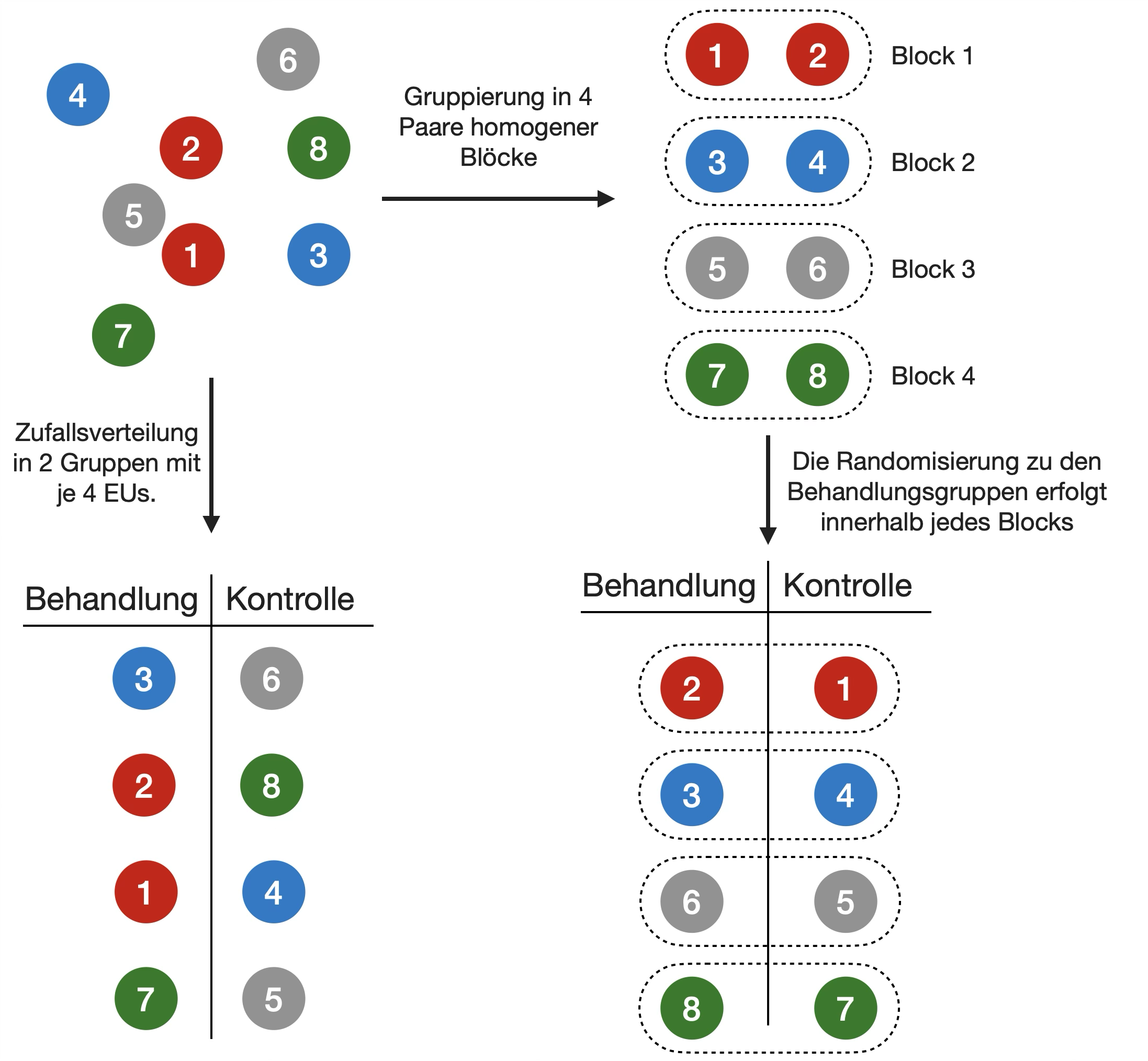
Übernommen aus:

Lazic (2016) Experimental Design for Laboratory Biologists

Feste vs. zufällige Effekte

  • Die Behandlungseffekte, biologischen und technischen Effekte lassen sich in 2 Typen unterscheiden: fest (fixed) und zufällig (random).
  • Die Unterscheidung ist wichtig, weil sie zu unterschiedlichen Analysen und Interpretationen der Ergebnisse führen.
  • Ob ein kategorialer Prädikator fest oder zufällig ist, hängt nur davon ab, wie wir es definieren wollen!

Feste Effekte → Behandlungseffekte

  • Die meisten Standardtests gehen von festen Faktoren aus.
  • Die einzelnen Faktorstufen beziehen sich auf den Mittelwert von Y.

Zufällige Effekte → biologische/technische Eff.

  • Die einzelnen Faktorstufen beziehen sich auf die Varianz von Y.
  • Zufällige Effekte sind meist weniger interessant.
  • Haben meist viele Faktorstufen

Kontrollen

Negative Kontrollen

  • 2 Typen:
    • Verfahrenskontrolle (‘Placebo’): Ähnliches Verfahren außer für die eigentliche Behandlung, z.B. Injektion von Kochsalzlösung anstelle von Medikamenten,.
    • Naive Kontrolle: nützlich, wenn die Handhabung der Behandlung (z.B. die Injektion selbst) eine Wirkung hat.
  • Wenn kein Unterschied zwischen beiden Kontrollen besteht, können sie zusammengelegt werden, um die Probengröße zu erhöhen.

Positive Kontrollen

  • Zusätzliche Behandlung, von der bekannt ist, dass sie eine Wirkung hat → Baseline
  • Nützlich, um zu prüfen, ob die EU überhaupt reagiert → Test ob Versuchsaufbau geeignet ist.
  • Bei großer Wirkungsstärke der Behandlung keine Positivkontrolle erforderlich.

Blindproben

Blindproben und Doppel-Blindproben

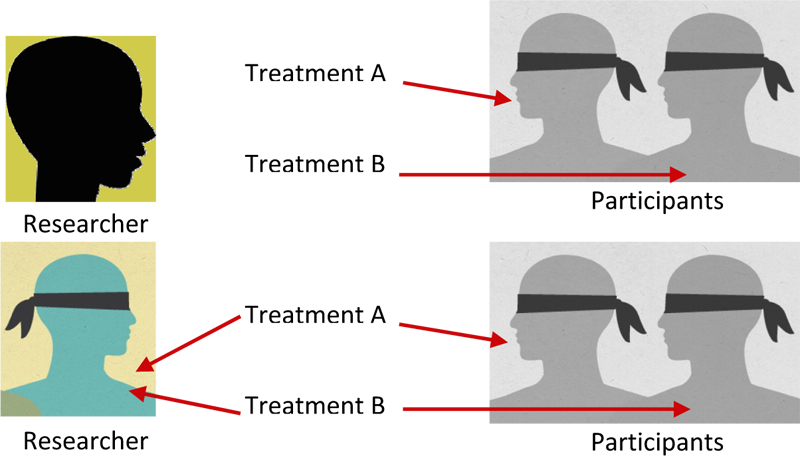
Front- (FA) vs. end-alignment (EA)

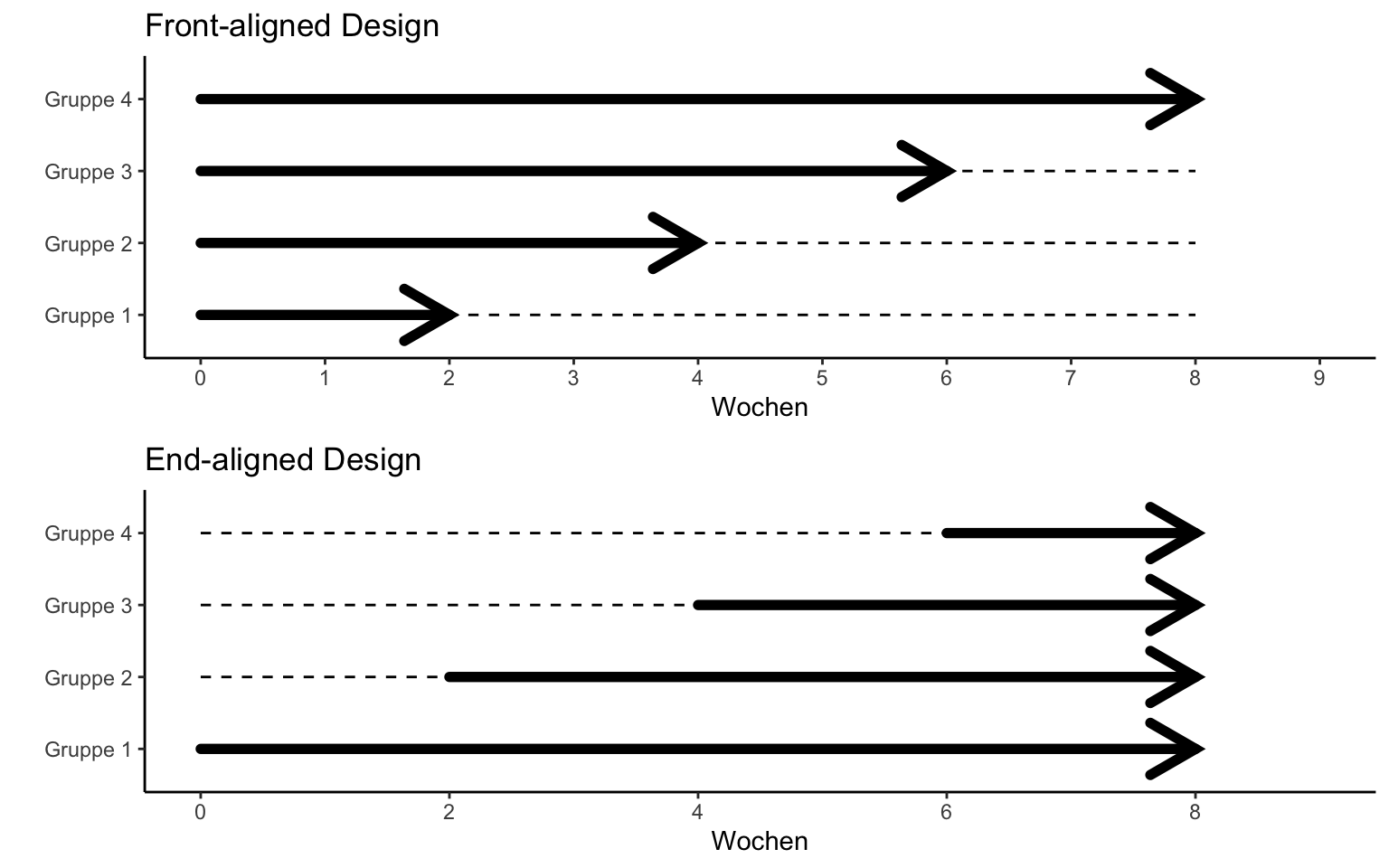
→ Je länger die Dauer, desto besser ein EA-Design!

Störeffekte | 1

Störeffekte | 2

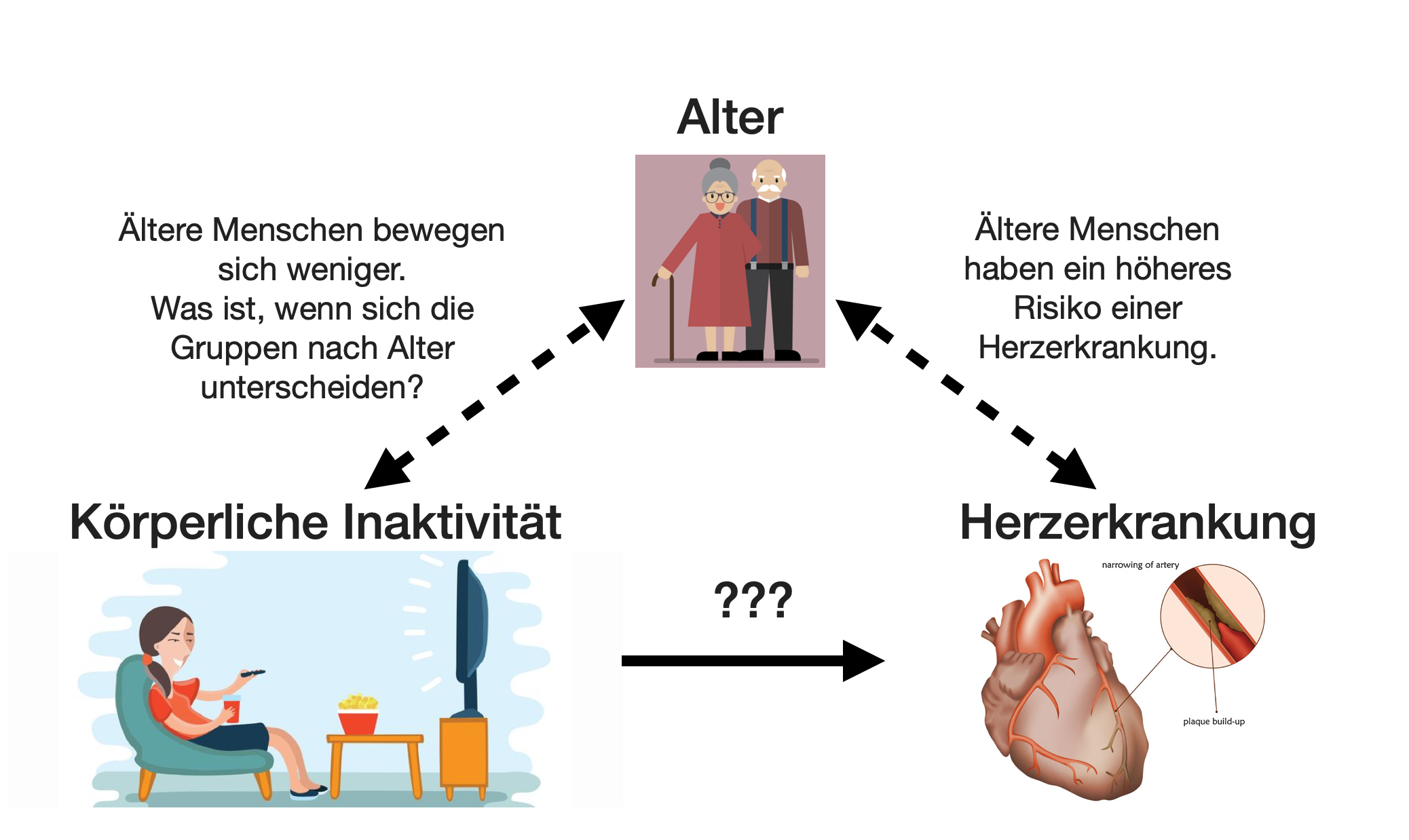
Störeffekte | 3

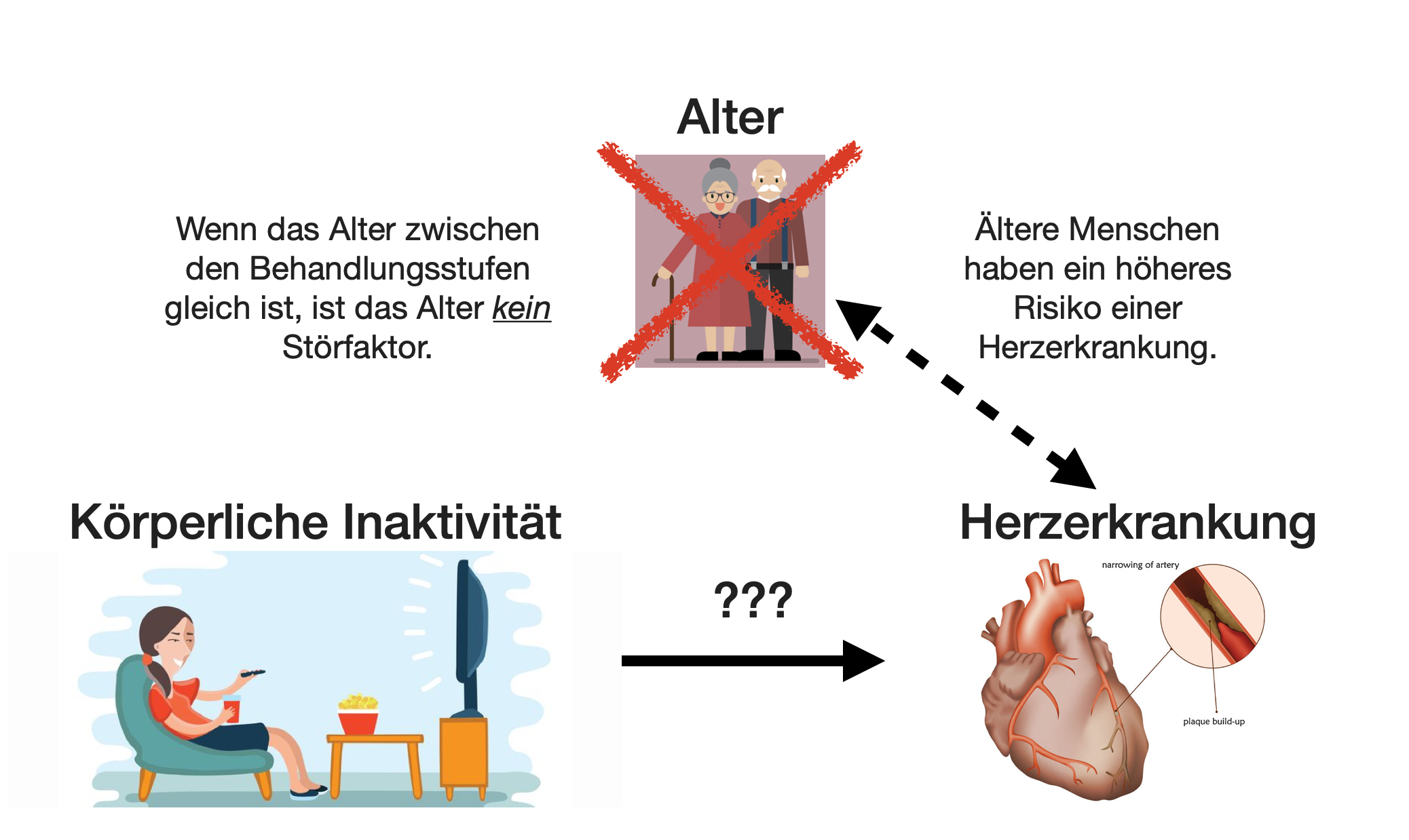
Störeffekte | 4

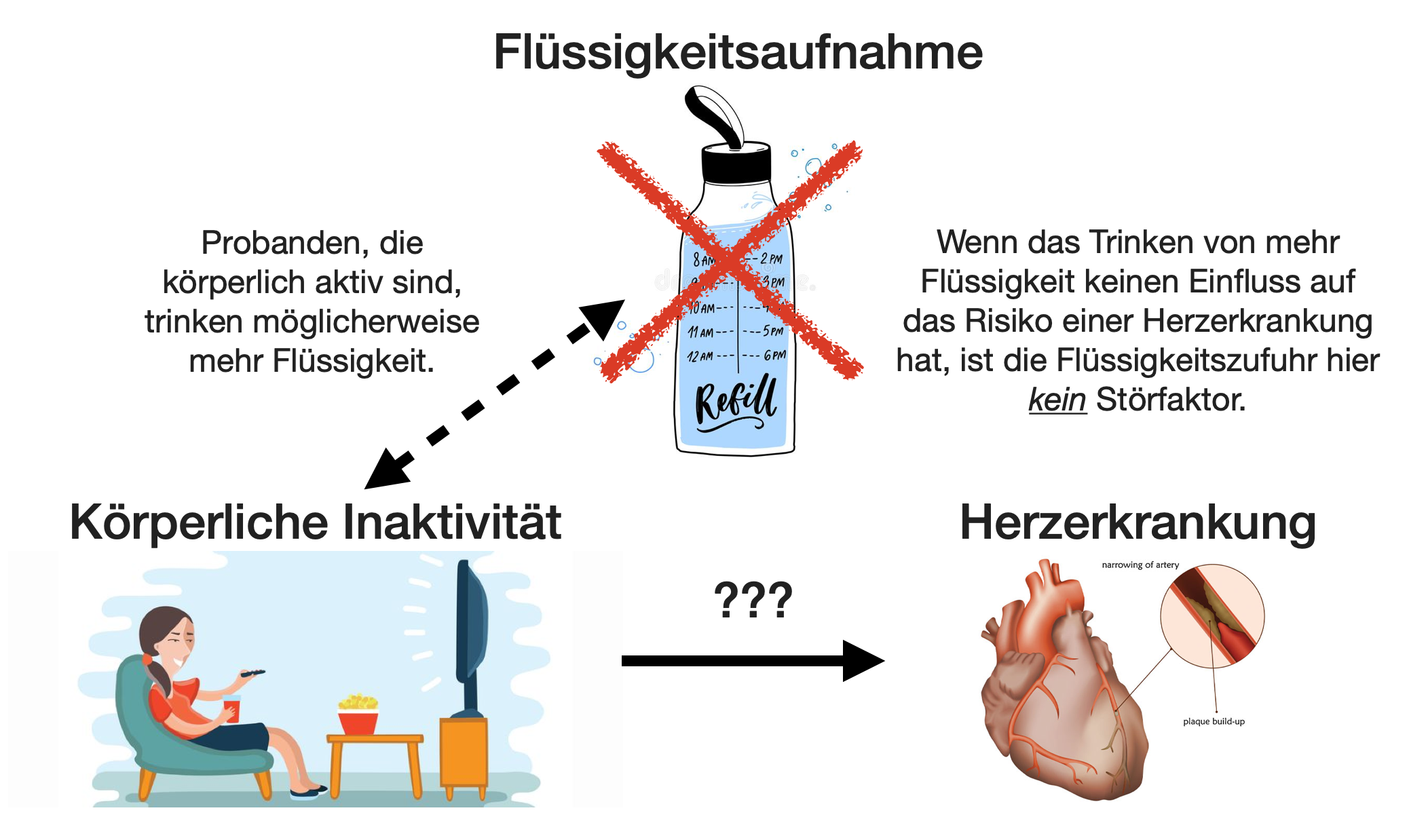
Störeffekte | 5

  • Der interessierende Faktor sollte isoliert werden.
  • Eine oder besser zwei Kontrollen im Experiment verwenden.
  • Wenn Störfaktoren unvermeidbar sind sollte das Experiment so gestaltet werden, dass die Auswirkungen getestet werden können.
    • → Abwägen, welcher biologische/technische Effekt am meisten stört.

Replikation

  • Jede Einheit mit der gleichen Behandlung wird als Replikat bezeichnet.
  • Liefert uns ein Maß für die natürliche Variabilität (“Fehler”-Variation).
  • Muss auf der korrekten Stufe liegen, um präzise Schlüsse ziehen zu können.
  • Replikate müssen unabhängig sein, um Beeinträchtigungen zu vermeiden!

Pseudoeplikation

  • Statistisch abhängige Replikate
  • Oft durch zeitliche oder räumliche Abhängigkeiten (Zeitserien, geografische Daten)

Quelle: Hurlbert (1984) Pseudoreplication and the Design of Ecological Field Experiments

Planungsoptimierung - Accuracy und Precision

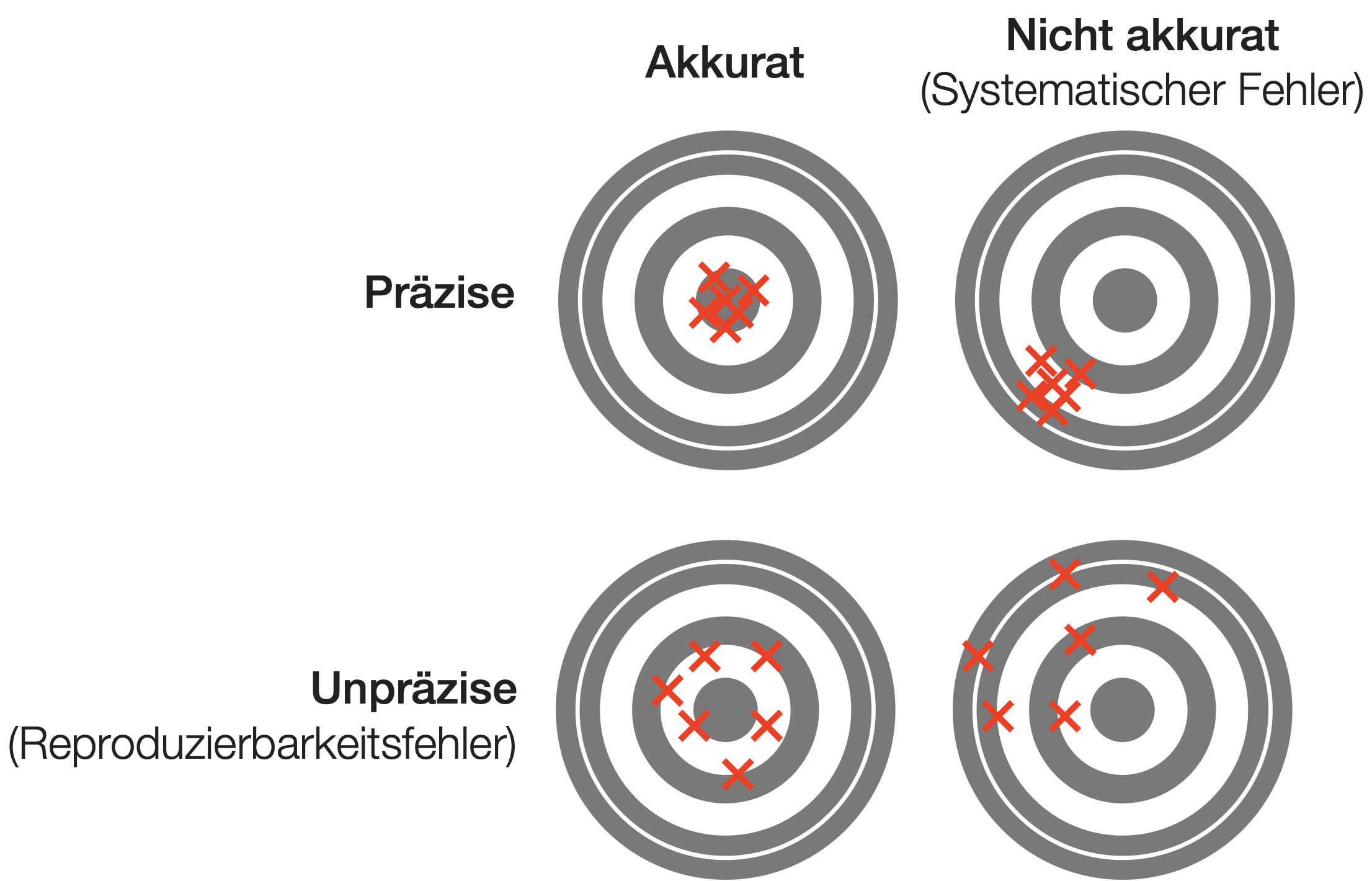
Accuracy (~Treffgenauigkeit) = Nähe einer Schätzung zum wahren Wert des zu schätzenden Parameters.

Precision (~Exaktheit) = Grad der Übereinstimmung zwischen wiederholten Schätzungen.

Poweranalyse und Berechnung des Stichprobenumfangs

Übliche Experimentfragen

Nachdem das Design des Experiments und die statistische Analyse bestimmt wurden, ergeben sich oft folgende 3 Fragen:

  1. Welcher Stichprobenumfang ist nötig?
  2. Wie hoch ist die Power oder Teststärke des Experiments?
  3. Was ist der kleinste Effekt, der mit dem Experiment nachgewiesen werden kann?

Power, Teststärke oder Trennschärfe eines Tests

  • Die Fähigkeit eines Tests, Unterschiede (Effekte) zu erkennen, wenn sie in Wirklichkeit vorhanden sind.
  • Definiert als 1-\beta → repräsentiert die Wahrscheinlichkeit, dass der Test eine falsche Nullhypothese ablehnt bzw. dass er keinen Fehler 2. Art macht.
  • Je höher die Teststärke, desto größer ist die Chance, ein statistisch signifikantes Ergebnis zu erhalten, wenn die Nullhypothese falsch ist.
  • Die sog. Power-Analyse kann ein nützliches Werkzeug für die Planung eines Experiments und die Schätzung der Stichproben- und Effektgröße sein.

Die universale Power-Gleichung

Zusammenhang

Power \propto \frac{ES~\alpha~\sqrt{n}}{\sigma^2}

Die Teststärke steigt proportional* mit

  • steigender Effektgröße ES
  • steigendem \alpha (wenn das Signifikanzniveau weniger strikt wird)
  • zunehmendem Stichprobenumfang n
  • abnehmender Varianz \sigma^2

→ Durch Umstellung der Gleichung kann jede dieser 5 Größen berechnet werden, wenn die anderen 4 gegeben sind.

*Wie genau die Teststärke sich ändert, hängt von der Analyse ab.

Berechnung der Effektgrößen Cohen (1992)

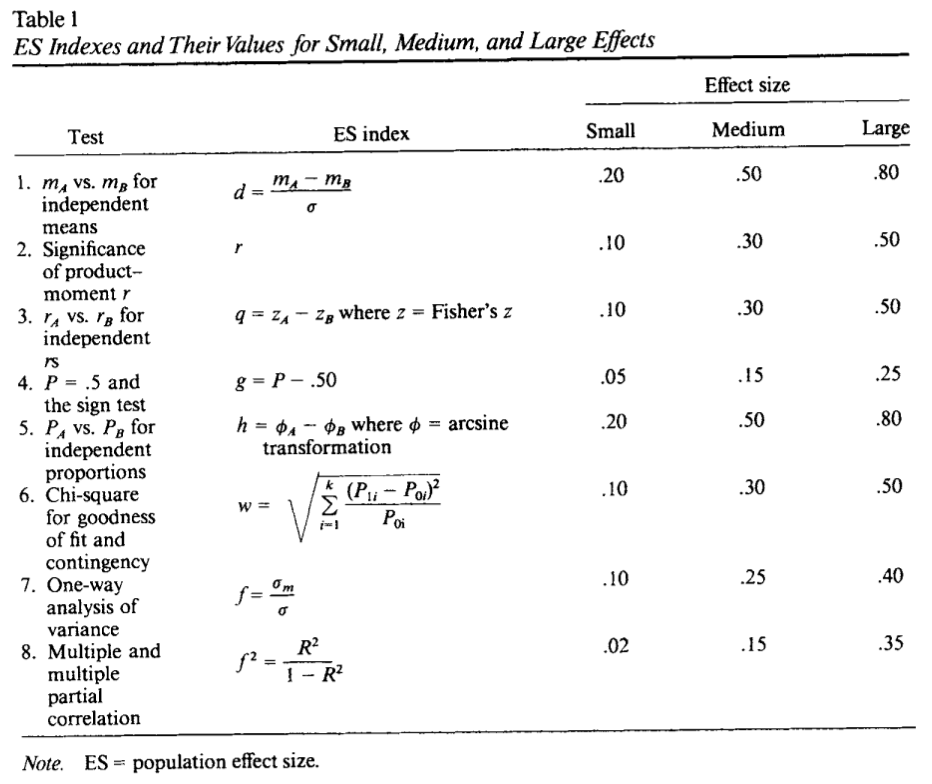
Cohen, J. (1992): A Power Primer, Psychological Bulletin 112(1): 155-159

t-Test | Berechnung des Stichprobenumfangs

n beim unabhängigen t-Test

Um die Stichprobengröße für einen unabhängigen t-Test zu ermitteln, brauchen wir einfach nur die Formel der Teststatistik nach n umwandeln. Es gilt für gleiche Varianzen und Stichprobengrößen:

t=\frac{(\bar{X}_1-\bar{X}_2)}{\sqrt{2\frac{s_p^2}{n}}}=\frac{d}{\sqrt{2\frac{s_p^2}{n}}}~~\Rightarrow~~\sqrt{2\frac{s_p^2}{n}}=\frac{d}{t}~~\Rightarrow~~2\frac{s_p^2}{n}=\frac{d^2}{t^2}~~\Rightarrow~~n = \frac{2t^2s_p^2}{d^2}

  • s_p ist die gepoolte Standardabweichung bei gleicher Stichprobengröße: \sqrt{\frac{s_1^2+s_2^2}{2}}
  • t hängt von der Wahl der Power und des Signifikanzniveaus ab.
  • Werden diese auf 1-\beta = 0.8 und \alpha = 0.05 gesetzt, so beträgt t = 2.8 und t^2 = 7.84 \approx 8 (die Quantilen einer Normalverteilung bei 0.05/2 und 0.8 werden addiert).
  • Somit gilt: n = \frac{2*8*s_p^2}{d^2}

Zum Glück gibt es auch R Funktionen

  • Basisfunktionen:
    • t-Test: power.t.test()
    • Zweistichprobentest für Proportionen: power.prop.test()
    • 1-faktorielle ANOVA: power.anova.test()
Beispiel t-Test
power.t.test(n = NULL, delta = NULL, sd = 1, sig.level = 0.05,
             power = NULL,
             type = c("two.sample", "one.sample", "paired"),
             alternative = c("two.sided", "one.sided"),
             strict = FALSE, tol = .Machine$double.eps^0.25)

t-Test | Beispiel Zugverhalten

Wie groß muss die Stichprobe sein, damit der von uns beobachtete Unterschied von 1200 km statistisch nachweisbar ist?

Kenngröße Buchfink Mönchsgrasmücke
Mittelwert x̅ 1800 km 3000 km
Standardabweichung s ±900 km ±1000 km
Stichprobengröße n 20 30

Buchfink

Mönchsgrasmücke

Bildquellen: Wikipedia (Buchfink unter (CC BY-SA 2.5 Lizenz) und Mönchsgrasmücke unter CC0 Lizenz)

t-Test | Berechnung von n

Wie groß muss die Stichprobe sein, damit der von uns beobachtete Unterschied von 1200 km statistisch nachweisbar ist?

d <- abs(1800-3000)
s_p <- sqrt((900^2 + 1000^2) / 2)
n <- (16*s_p^2) / d^2
n
[1] 10.056
power.t.test(power=0.8, sd=s_p, delta=d)

     Two-sample t test power calculation 

              n = 10.915
          delta = 1200
             sd = 951.31
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

NOTE: n is number in *each* group
  • → Es braucht mindestens 10 Replikate pro Gruppe.

t-Test | Berechnung von n

Und wie groß müsste die Stichprobe sein, wenn wir bereits einen Unterschied von 600 km bzw. 300 km statistisch nachweisen wollen?

delta von 600 km
power.t.test(power = 0.8, sd = s_p, 
  delta = 600)

     Two-sample t test power calculation 

              n = 40.446
          delta = 600
             sd = 951.31
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

NOTE: n is number in *each* group
delta von 300 km
power.t.test(power = 0.8, sd = s_p, 
  delta = 300)

     Two-sample t test power calculation 

              n = 158.82
          delta = 300
             sd = 951.31
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

NOTE: n is number in *each* group

t-Test | Poweranalyse

Im vorliegenden Experiment betrug der Stichprobenumfang 20 und 30. Wie hoch wäre die Teststärke bei 20 oder bei 5 Vogelmessungen (in beiden Gruppen) gewesen, um einen Unterschied von 1200 km statistisch nachweisen zu können?

N = 20
power.t.test(n = 20, sd = s_p, delta = d)

     Two-sample t test power calculation 

              n = 20
          delta = 1200
             sd = 951.31
      sig.level = 0.05
          power = 0.97297
    alternative = two.sided

NOTE: n is number in *each* group
N = 5
power.t.test(n = 5, sd = s_p, delta = d)

     Two-sample t test power calculation 

              n = 5
          delta = 1200
             sd = 951.31
      sig.level = 0.05
          power = 0.41908
    alternative = two.sided

NOTE: n is number in *each* group

t-Test | Berechnung des minimal
nachweisbaren Effektes

Angenommen es soll die Untersuchung des Zugverhaltens wiederholt werden, es können aber nur 8 Vögel jeweils untersucht werden. Welche Differenz könnte dann überhaupt statistisch nachgewiesen werden?

N = 5
power.t.test(power = 0.8, n = 8, sd = s_p)

     Two-sample t test power calculation 

              n = 8
          delta = 1433.3
             sd = 951.31
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

NOTE: n is number in *each* group



→ Die Differenz müsste mindestens 1433.3 km betragen, um überhaupt einen signifikanten Unterschied zwischen den beiden Arten nachweisen zu können.

t-Test | Sog. ‘Power Curves’ 1

Anstatt immer nur einzelne Szenarios durchzuspielen, ist es hilfreich, die Teststärke für mehrere Kombinationen an Parametern als Kurve zu visualisieren:

# Erstellen eines df mit versch. Kombinationen
df <- expand.grid(
  n = seq(5, 40, 2), 
  sd = c(500,750,1000, 1250), 
  delta = c(500,1000), 
  power = NA
)
dim(df)
[1] 144   4
# Powerberechnung für jede der 144 Kombinationen
for (i in 1:nrow(df)) {
  df$power[i] <- power.t.test(n = df$n[i], sd = df$sd[i], 
    delta = df$delta[i])$power
}
head(df)
   n  sd delta   power
1  5 500   500 0.28593
2  7 500   500 0.40570
3  9 500   500 0.51333
4 11 500   500 0.60708
5 13 500   500 0.68671
6 15 500   500 0.75292

t-Test | Sog. ‘Power Curves’ 2

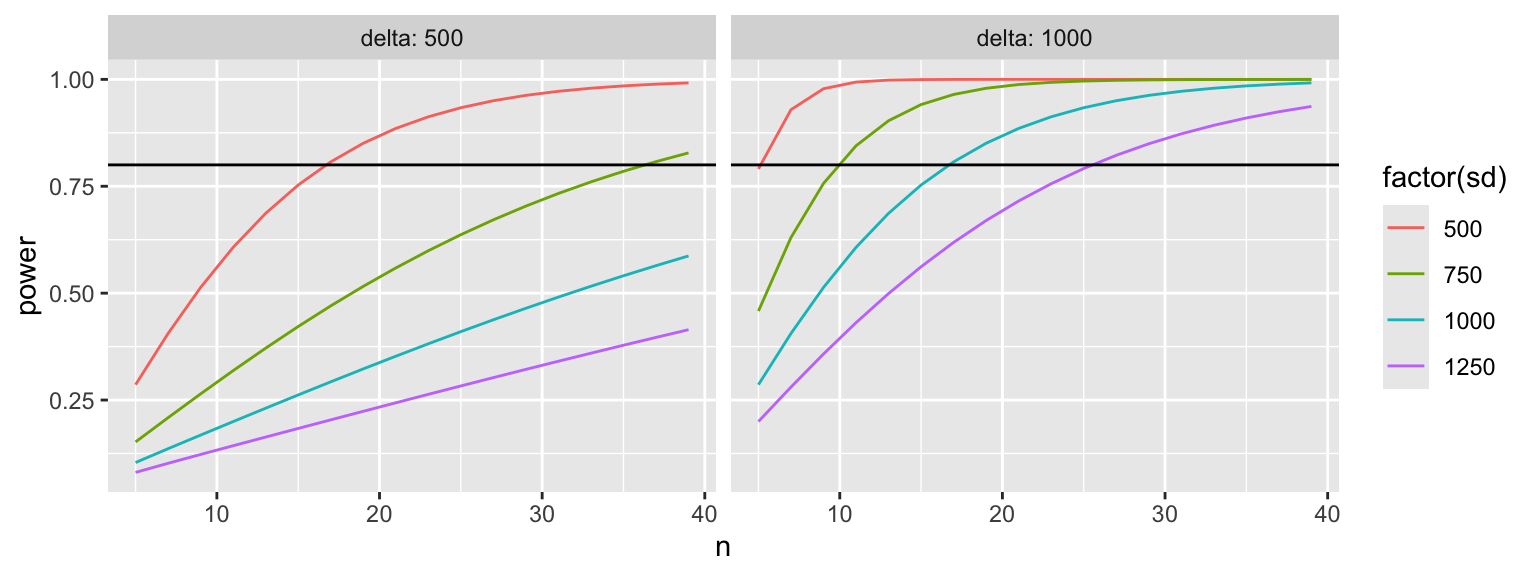
df |> ggplot(aes(n, power, group = sd, color = factor(sd))) + geom_line() + 
  geom_hline(yintercept = 0.8) + facet_grid(~delta, labeller = label_both)
  • Bei hoher Effektgröße und geringer Variabilität wird die nicht-lineare Beziehung zwischen der Stichprobengröße und der Power sichtbar.
    • → Kleine Erhöhungen des Stichprobenumfangs führen hier bereits zu großen Erhöhungen der Teststärke.
  • Die Kurve macht schnell deutlich, dass ein n von 40 nicht ausreicht um eine Power von 0.8 zu erzielen, wenn die Standardabweichung >750 ist und die Differenz bei nur 500 km liegt.

ANOVA | Berechnung des Stichprobenumfangs

Die Funktion
power.anova.test(groups = NULL, n = NULL,
                 between.var = NULL, within.var = NULL,
                 sig.level = 0.05, power = NULL)


Input-Paramater

  • groups: Anzahl der Gruppen
  • n: Stichprobenumfang pro Gruppe (Annahme balanciertes Design)
  • between.var: Varianz zwischen den Gruppen
  • within.var: Varianz innerhalb der Gruppen
  • sig.level: Signifikanzniveau
  • power: Teststärke

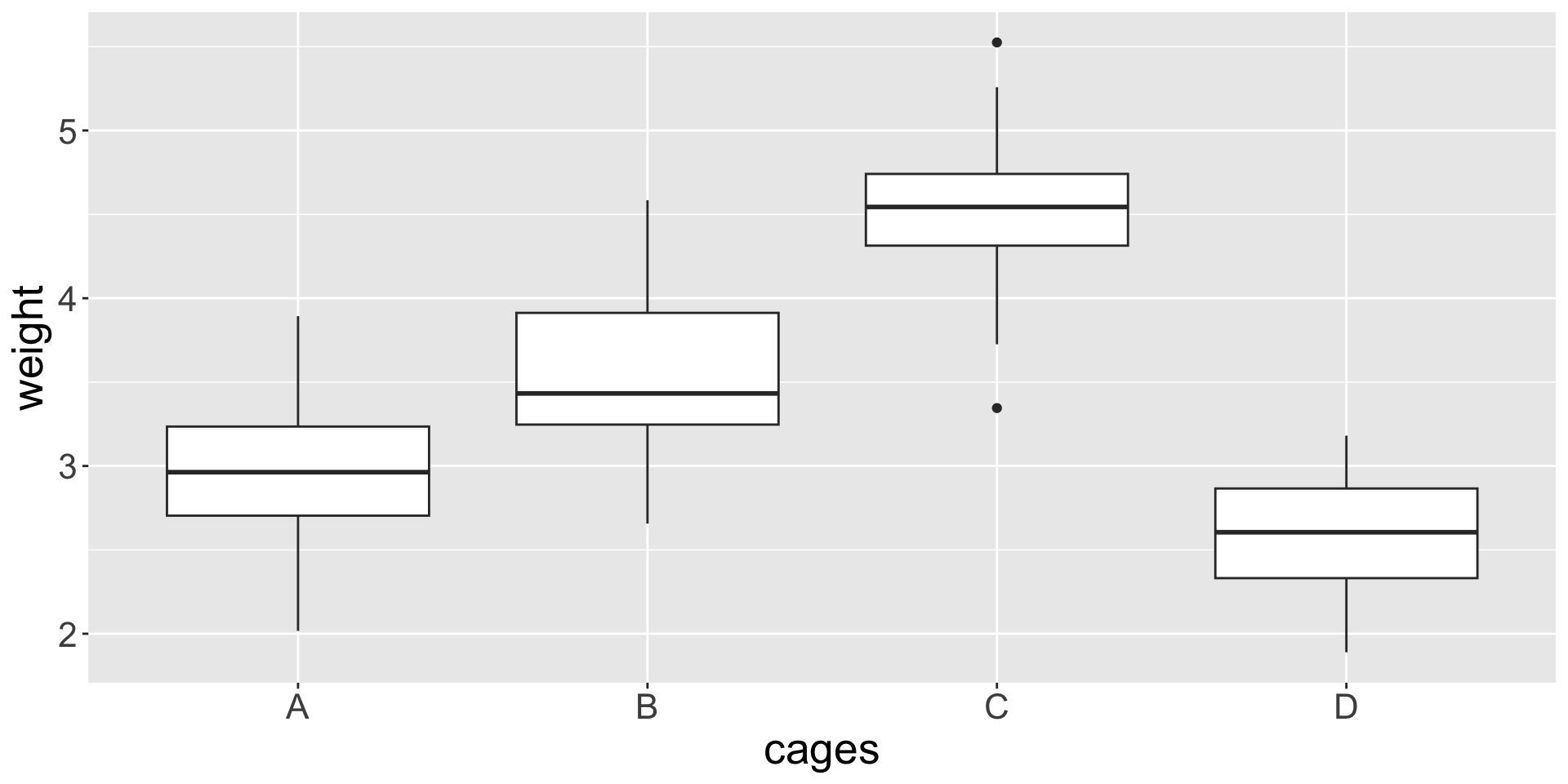
ANOVA | Berechnung von n - Lachs-Beispiel

Gewichtsunterschiede von Atlantischem Lachs, der in 4 verschiedenen Typen von Netzkäfigen gezüchtet wurde (n = 24).

df <- salmon |>  group_by(cages) |> 
  summarise(mean = mean(weight), 
    var = var(weight))
power.anova.test(groups = 4, 
  between.var = var(df$mean), 
  within.var = mean(df$var), 
  power = 0.8)

     Balanced one-way analysis of variance power calculation 

         groups = 4
              n = 2.2858
    between.var = 0.70366
     within.var = 0.20159
      sig.level = 0.05
          power = 0.8

NOTE: n is number in each group

Berücksichtigungen

Es gelten die gleichen Annamen

  • Die Poweranalyse und Stichprobenkalkulation basieren auf den gleichen Annahmen wie die zugrunde liegenden Tests:
    • Für eine zuverlässige Poweranalyse und Stichprobenkalkulation beim t-Test muss die Normalitätsannahme für jede Gruppe erfüllt sein.
    • Bei der Poweranalyse für eine ANOVA müssen alle Gruppen dazu die gleiche Varianz haben, damit dem Ergebnis vertraut werden kann.

Hilfreiche Pakete

  • pwr: Funktionen für weitere Tests und Design gibt es in diesem R Paket von Stéphane Champely, welches sich an Cohen (1988) orientiert (siehe auch die Vignette)
  • MKpower: Power-Analyse und Berechnung der Stichprobengröße für Welch und Hsu t-Test.
  • WMWssp: Berechnet den minimalen Stichprobenumfang für den Mann-Whitney U-Test.
  • MultNonParam: Sammlung multivariater nichtparametrischer Methoden, inkl. Funktionen zur Power-Analyse und Stichprobenberechnung für den Kruskal-Wallis-Test.
  • WebPower: Sammlung von Funktionen für simple Tests (z.B. einfache lineare Regression) bis komplexe lineare Modelle, SEMs, etc.
  • Superpower: Poweranalysen für komplexere ANOVA Designs
  • simglm: Spezialpaket für Poweranalysen mittels Simulationen
  • SIMR: Poweranalyse für Generalized Linear Mixed Effects Models

Weitere hilfreiche Funktionen

Funktion Poweranalyse für
pwr::pwr.t.test() t-Tests (1-2-Stichproben, unabhängig, gepaart)
pwr::pwr.t2n.test() t-Test (2-Stichproben, ungleiches n)
MKpower::power.welch.t.test() Welch t-Test
WMWssp::WMWssp() Mann-Whitney U-Test (nur Berechnung n)
pwr::pwr.chisq.test() Chi-Quadrat-Test
pwr::pwr.anova.test() Balanced one-way ANOVA (gleiches n)
MultNonParam::kwpower() und MultNonParam::kwsamplesize() Kruskal-Wallis-Test
pwr::pwr.r.test() Korrelation
WebPower::wp.regression() lineare Regression

(siehe auch begleitendes VL-Skript)

G*Power

Nützliche Open Source Software für Windows und Mac

Weblink zum Download:

https://www.psychologie.hhu.de/arbeitsgruppen/allgemeine-psychologie-und-arbeitspsychologie/gpower

G*Power | ANOVA-Demonstration

Lachs-Beispiel

df <- salmon |>  
  group_by(cages) |> 
  summarise(
    mean = mean(weight), 
    sd = sd(weight)
)
df
# A tibble: 4 × 3
  cages  mean    sd
  <fct> <dbl> <dbl>
1 A      3.00 0.479
2 B      3.53 0.469
3 C      4.53 0.481
4 D      2.59 0.354
mean(df$sd)
[1] 0.44584

Zusammenfassung

Vor Beginn der quantitativen Studie..

  • sollte das Modell und die Hypothese gut durchdacht, klar und spezifisch sein.
  • sollten folgende Punkte betrachtet werden:
    • untersuchte Grundgesamtheit
    • Designtyp und statistischer Test
    • Randomisierung, Repräsentativität, Replikation, Unabhängigkeit
    • Stichprobenumfang
    • möglichen Störeinflüsse
    • Quellen der Streuung
    • mögliche Pilotstudien

Literatur

Literaturempfehlungen

Bücher

Artikel

Fragen?

Abschlussquiz

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de

Creative Commons License
Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.

Kurswebseite: Data Science 2