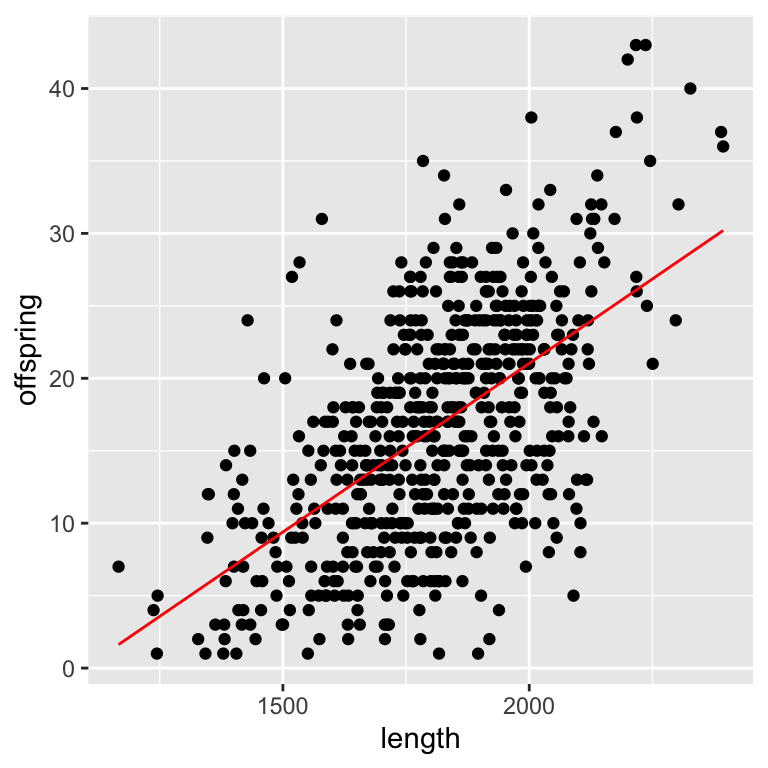
Call:
lm(formula = offspring ~ length, data = daphnia)
Coefficients:
(Intercept) length
-25.5385 0.0233 
10-Regression
Data Science 2
Saskia Otto & Monika Eberhard
Universität Hamburg, IMF & IZS
Sommersemester 2025
Lernziele

Nach Abschluss dieser VL und Übung..
- kennen Sie den Unterschied zwischen der Stichproben- und der Populationsgleichung.
- können Sie eine komplette lineare Regressionsanalyse in R durchführen und wissen Sie, wie der numerische Output zu interpretieren ist.
- wissen Sie, wie die Modellannahmen a priori und posteriori geprüft werden und wie die Diagramme zu interpretieren sind.
Frage des Tages
Hat die Größe der Weibchen bei Wasserflöhen der Art Daphnia galeata einen signifikanten Einfluss auf die Nachkommenzahl (pro Weibchen)? Und wenn ja, wie groß ist der Einfluss bzw. wie sehr kann die Größe die Variabilität der Nachkommenzahl erklären?
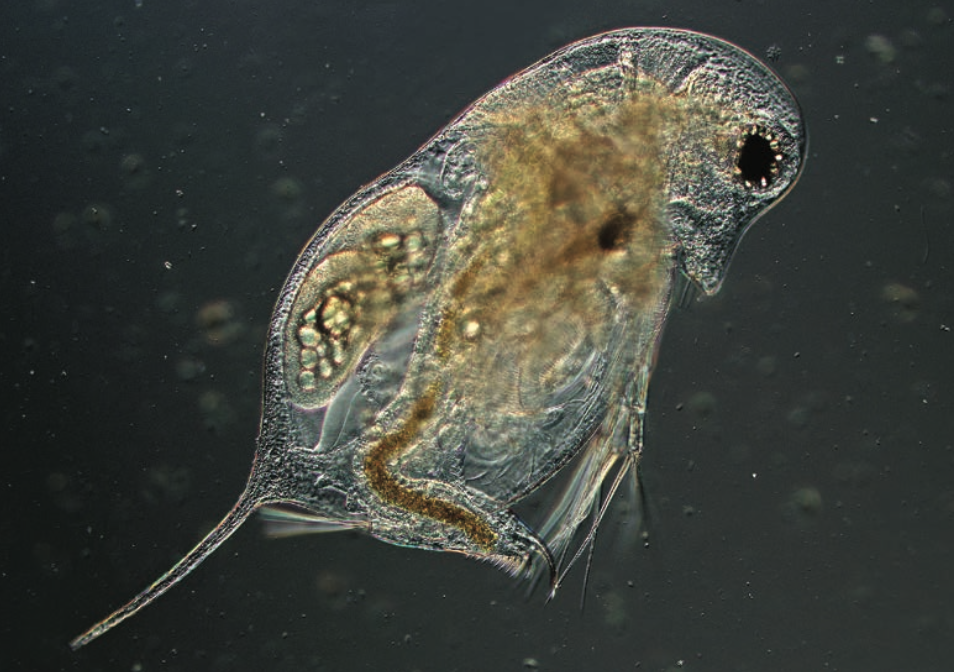
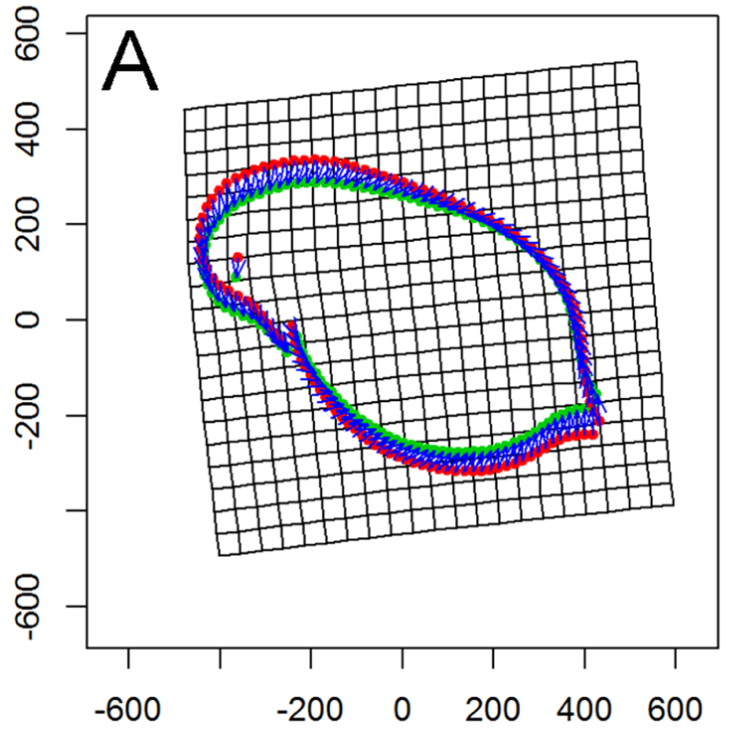
Bildquellen links: Znachor et al. (2016): Brief history of long-term ecological research into aquatic ecosystems and their catchments in the Czech Republic. Part I: Manmade reservoirs, Biology Centre CAS, Institute of Hydrobiology, České Budějovice; rechts: Tams et al. (2018): Intraspecific phenotypic variation in life history traits of Daphnia galeata populations in response to fish kairomones. PeerJ 6:e5746; DOI 10.7717/peerj.5746
Einführung

Lineares Regressionsmodelle in R | lm()

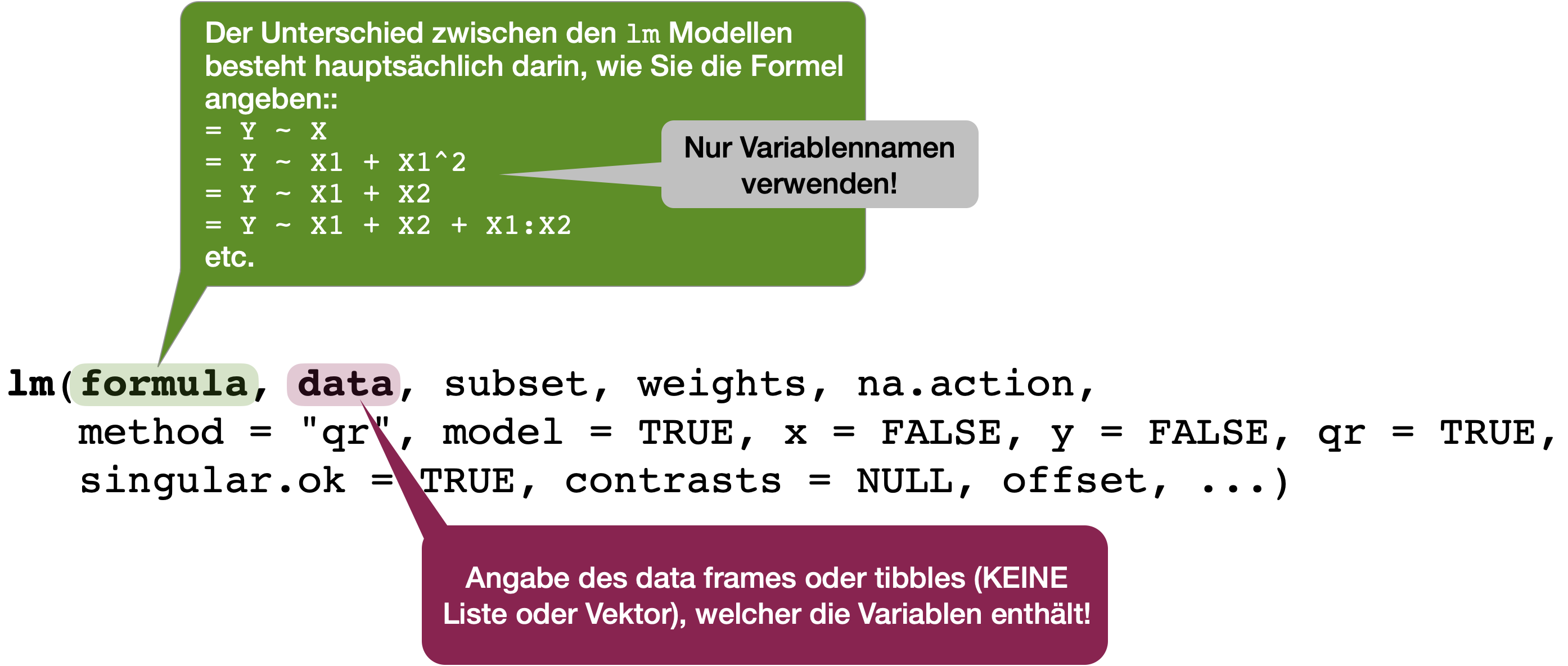
Anwendungsbeispiel daphnia

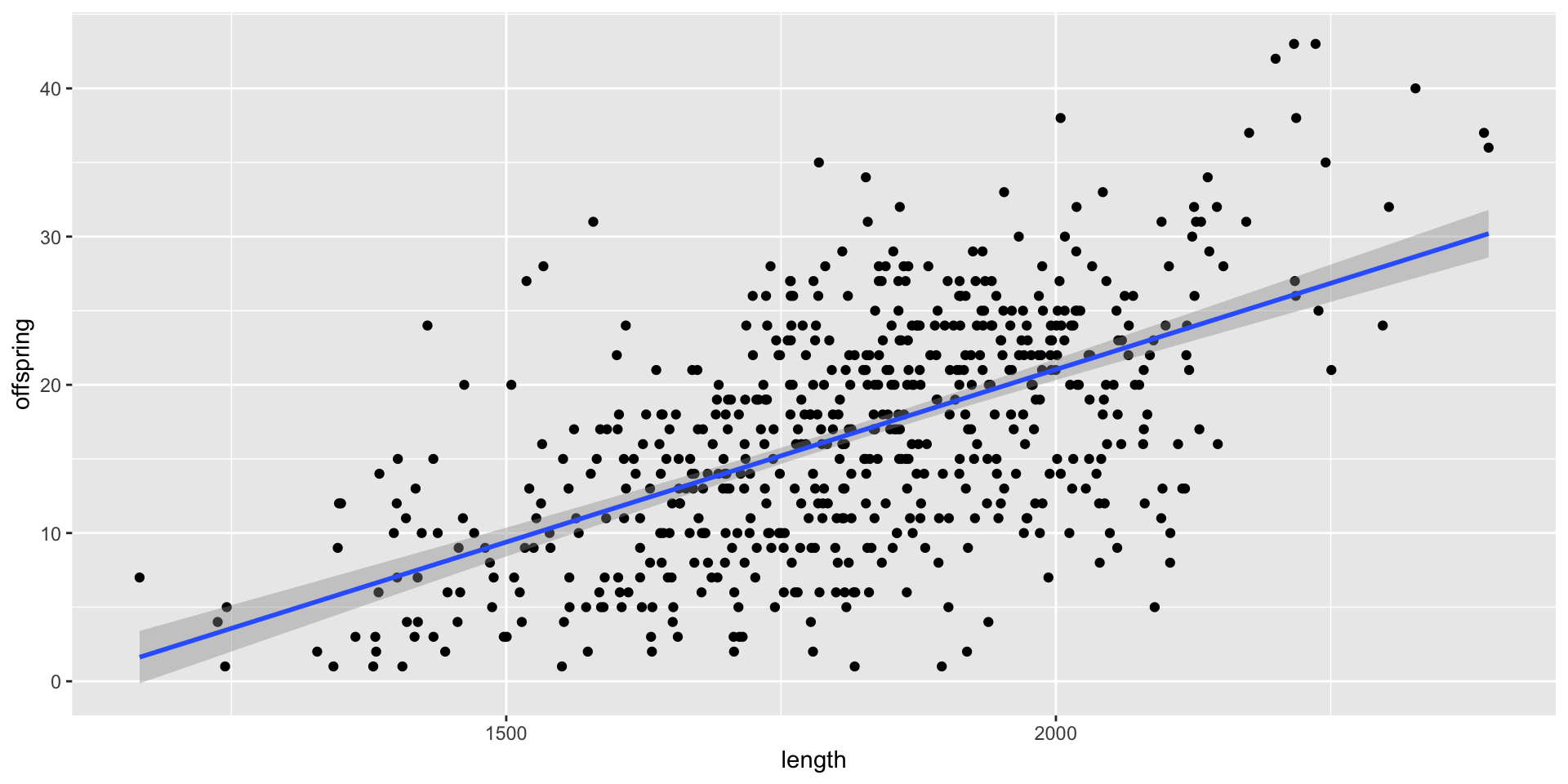
Wir modellieren die Anzahl an Nachkommen als Funktion der Größe der Wasserflohweibchen:
Beispiel aus Lektion 6 im Swirl-Kurs DSB-04-Datenvisualsierung mit ggplot2.
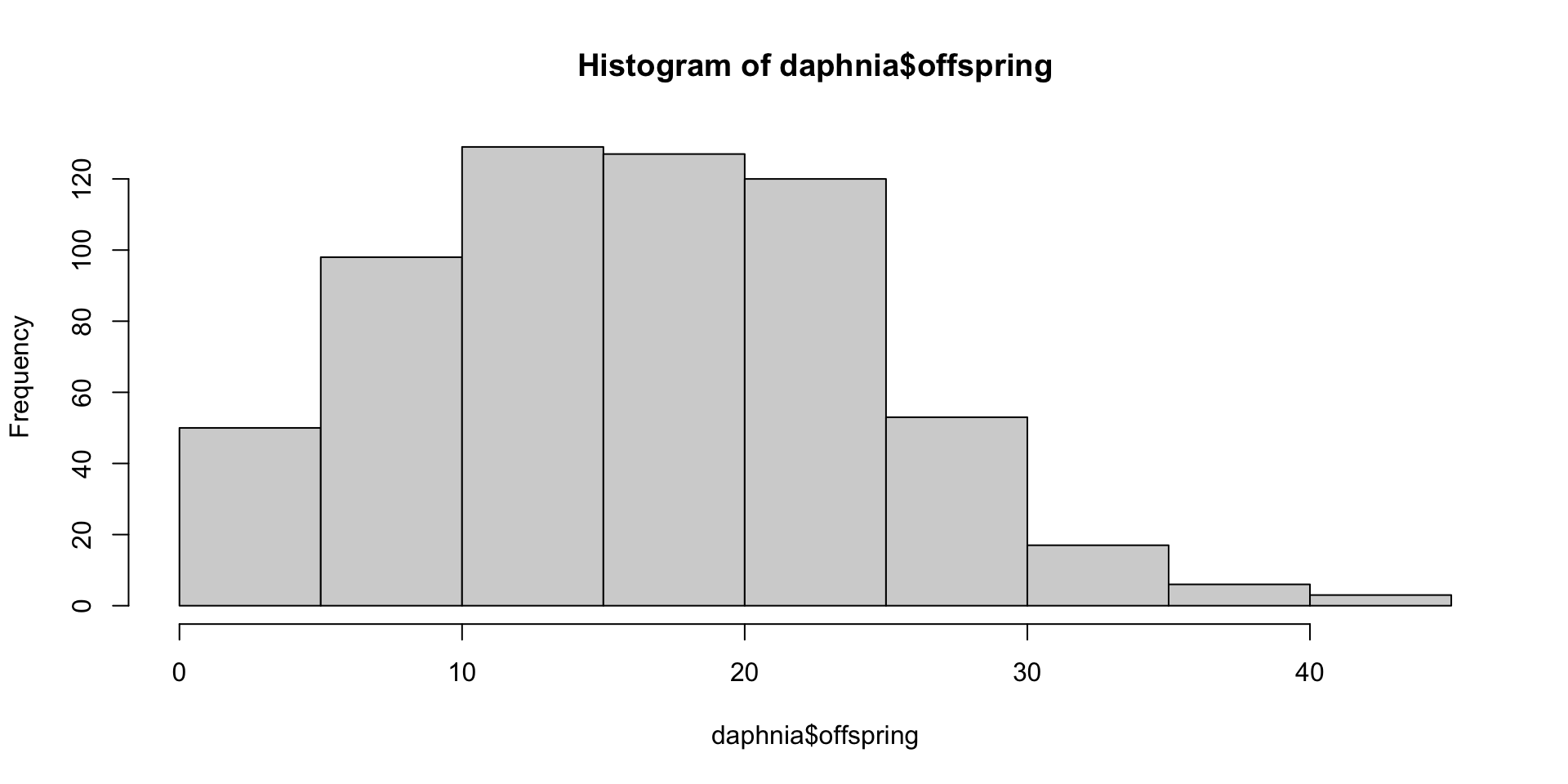
Shapiro-Wilk normality test
data: daphnia$offspring
W = 1, p-value = 4e-05→ Die Annahme der Normalverteilung der Antwortvariable ist erstmal nicht gegeben. Entscheidend ist aber letztendlich die Verteilung der Modellresiduen, die wir nach der Modellierung prüfen!
'data.frame': 603 obs. of 9 variables:
$ round : int 1 1 1 1 1 1 1 1 1 1 ...
$ exp_id : chr "FK274" "FK327" "FK328" "FK329" ...
$ pop : chr "G" "G" "G" "G" ...
$ treatment: chr "control" "control" "control" "control" ...
$ length : num 1817 1864 1779 1852 1902 ...
$ afr : int 8 9 11 10 10 10 10 10 9 8 ...
$ broods : int 1 3 1 2 2 2 2 2 2 3 ...
$ offspring: int 1 15 2 9 5 7 3 7 13 27 ...
$ repro : num 1 5 2 4.5 2.5 3.5 1.5 3.5 6.5 9 ...Wie lautet die vollständige lineare Regressionsgleichung?
Stichproben- vs. Populationsgleichung
Stichprobengleichung
- für beobachtete y-Werte1:\qquad y_{i} = a + b*x_{i} + \epsilon_{i}
- für vorhergesagte y-Werte: \qquad \hat{y}_i = a + b*x_{i}
Populationsgleichung
- für beobachtete y-Werte: \qquad y_{i} = \alpha + \beta*x_{i} + \epsilon_{i}
- für vorhergesagte y-Werte: \qquad \mu(y_{i}) = \alpha + \beta*x_{i}
- Die Stichprobenkennwerte a und b repräsentieren die Punktschätzer der Regressionsparameter \alpha und \beta!
Stichprobengleichung | Beispiel daphnia

Für die beobachteten Stichprobenwerte gilt:
offspring_i = -25.5 + 0.023*length_i + \epsilon_{i} ~~\text{wobei}~~\epsilon_i \sim N(\mu, \sigma^2)
R rechnet noch viel mehr aus

Call:
lm(formula = offspring ~ length, data = daphnia)
Residuals:
Min 1Q Median 3Q Max
-18.12 -4.77 0.26 4.37 19.77
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -25.53847 2.43119 -10.5 <2e-16 ***
length 0.02329 0.00133 17.5 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.51 on 601 degrees of freedom
Multiple R-squared: 0.337, Adjusted R-squared: 0.336
F-statistic: 305 on 1 and 601 DF, p-value: <2e-16Wo sind a und b? Und was bedeuten die anderen Zahlen…?

Die Genauigkeit der Schätzung

Von der Stichprobe auf die Grundgesamtheit verallgemeinern
- Wie wären die geschätzten Koeffizienten, wenn wir das Experiment wiederholen würden?
- Wo liegen die geschätzten Koeffizienten für die gesamte Population?
- → Hier braucht es die Berechnung der Standardfehler und Hypothesentests
Zur Erinnerung
Die Genauigkeit der Punktschätzung sollte immer durch den Standardfehler des Schätzers angegeben werden
→ je kleiner der Standardschätzfehler, desto größer ist die Effizienz des Schätzers.
Reproduzierbarkeit geschätzter Koeffizienten
Stellen Sie sich vor, jeder Datenpunkt repräsentiert einen individuellen Fisch und alle Datenpunkte zusammen repräsentieren eine Population.
Starke Streuung
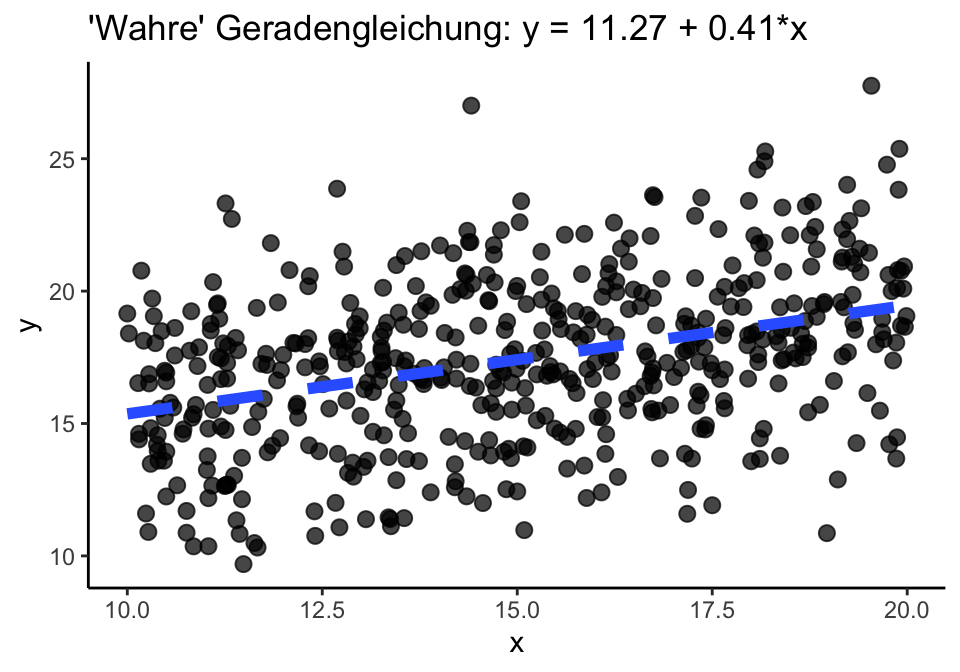
Schwache Streuung
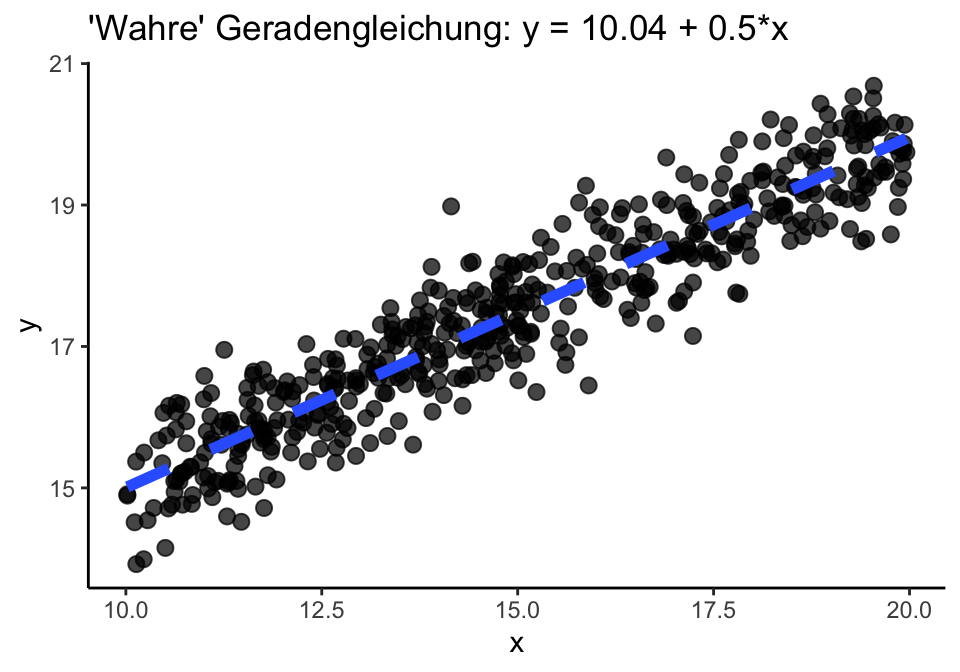
Wenn jetzt mehrere Zufallsproben von N Fischen genommen werden, wie ähnlich wären sich dann die geschätzten Koeffizienten?
Starke Streuung & N = 10 | 1
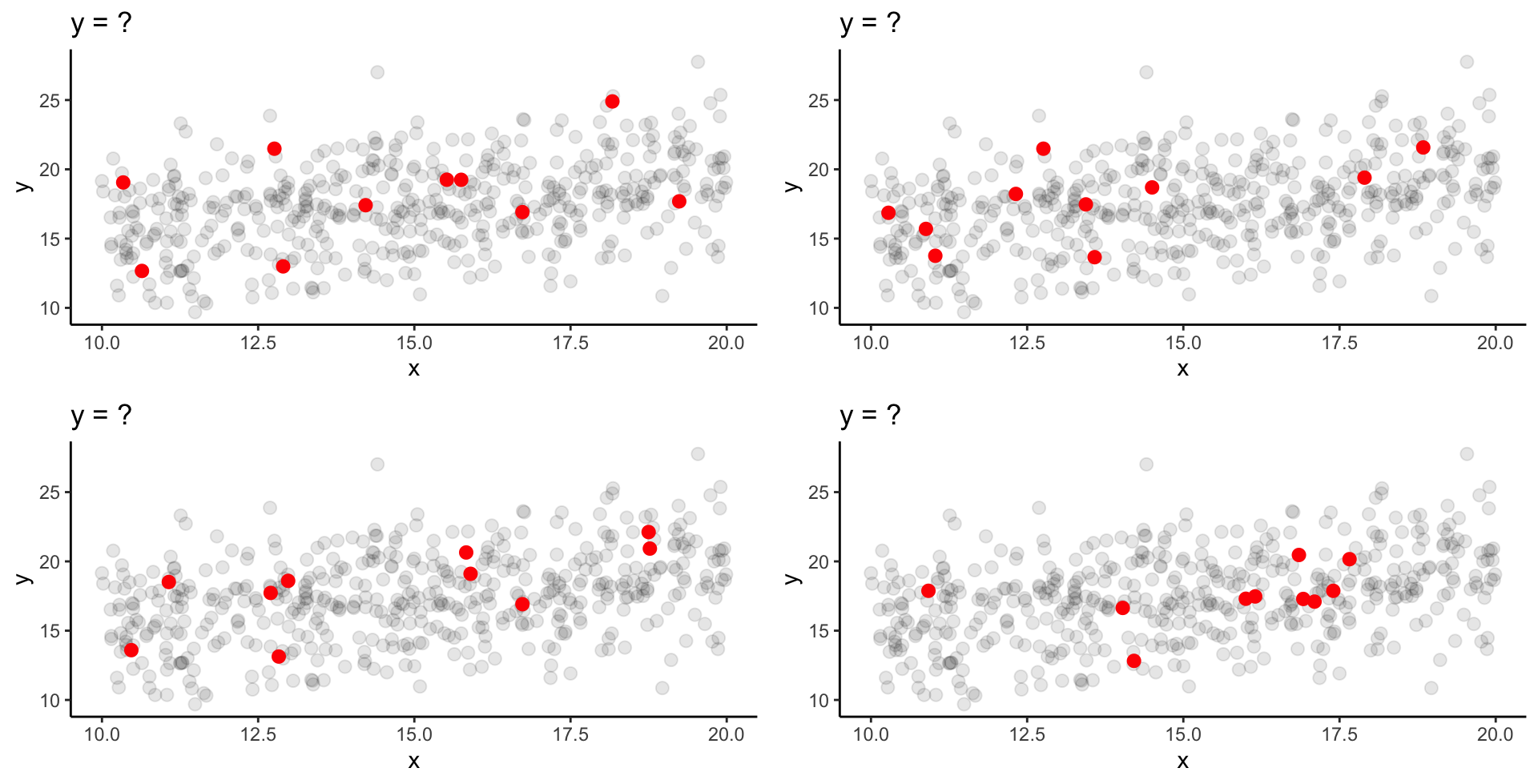
Welche sind sich viel ähnlicher und welche sind näher an den wahren Populationskoeffizienten dran?
Starke Streuung & N = 10 | 2
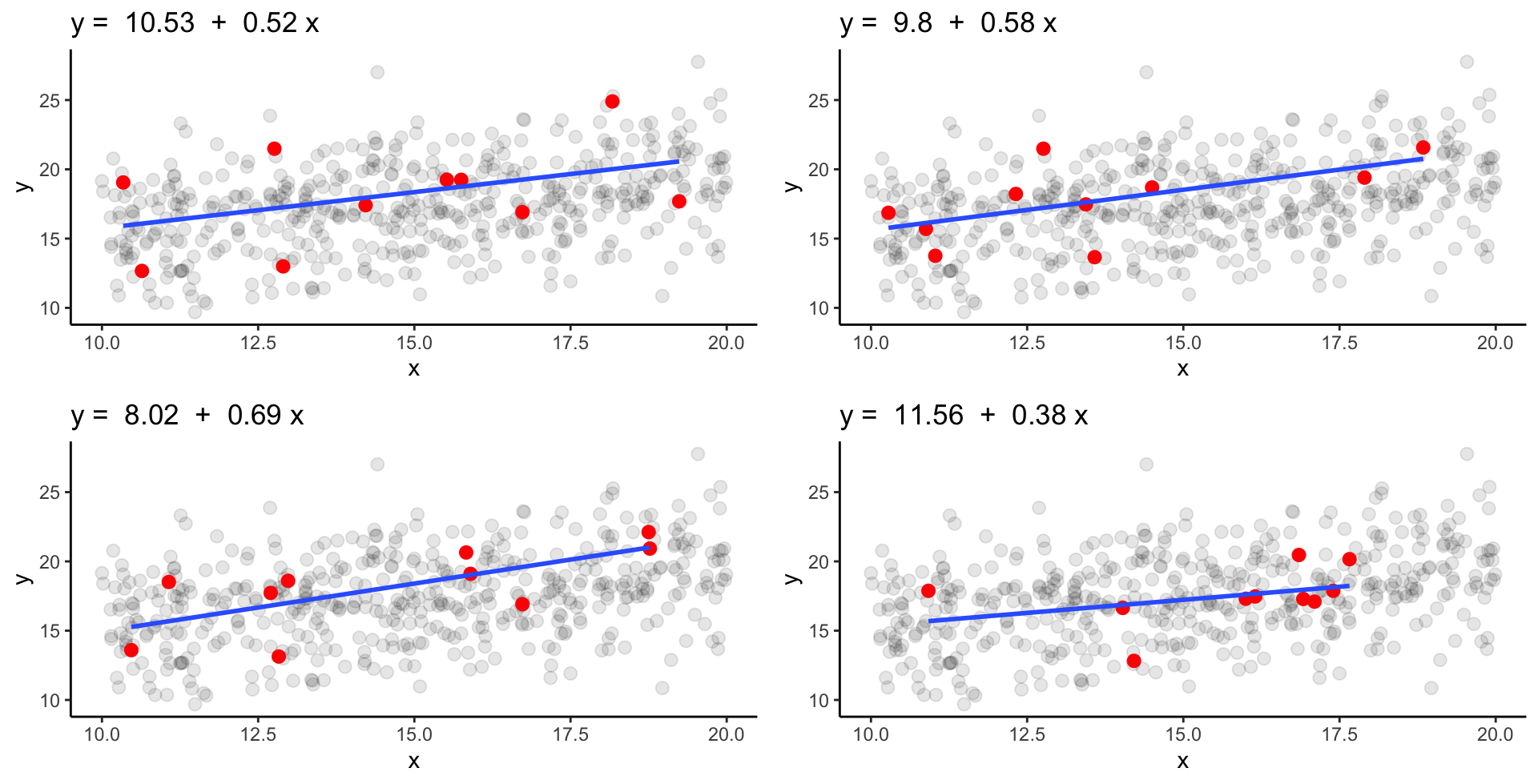
‘Wahre’ Parameter: \alpha = 11.27 und \beta = 0.41
Starke Streuung & N = 100 | 1
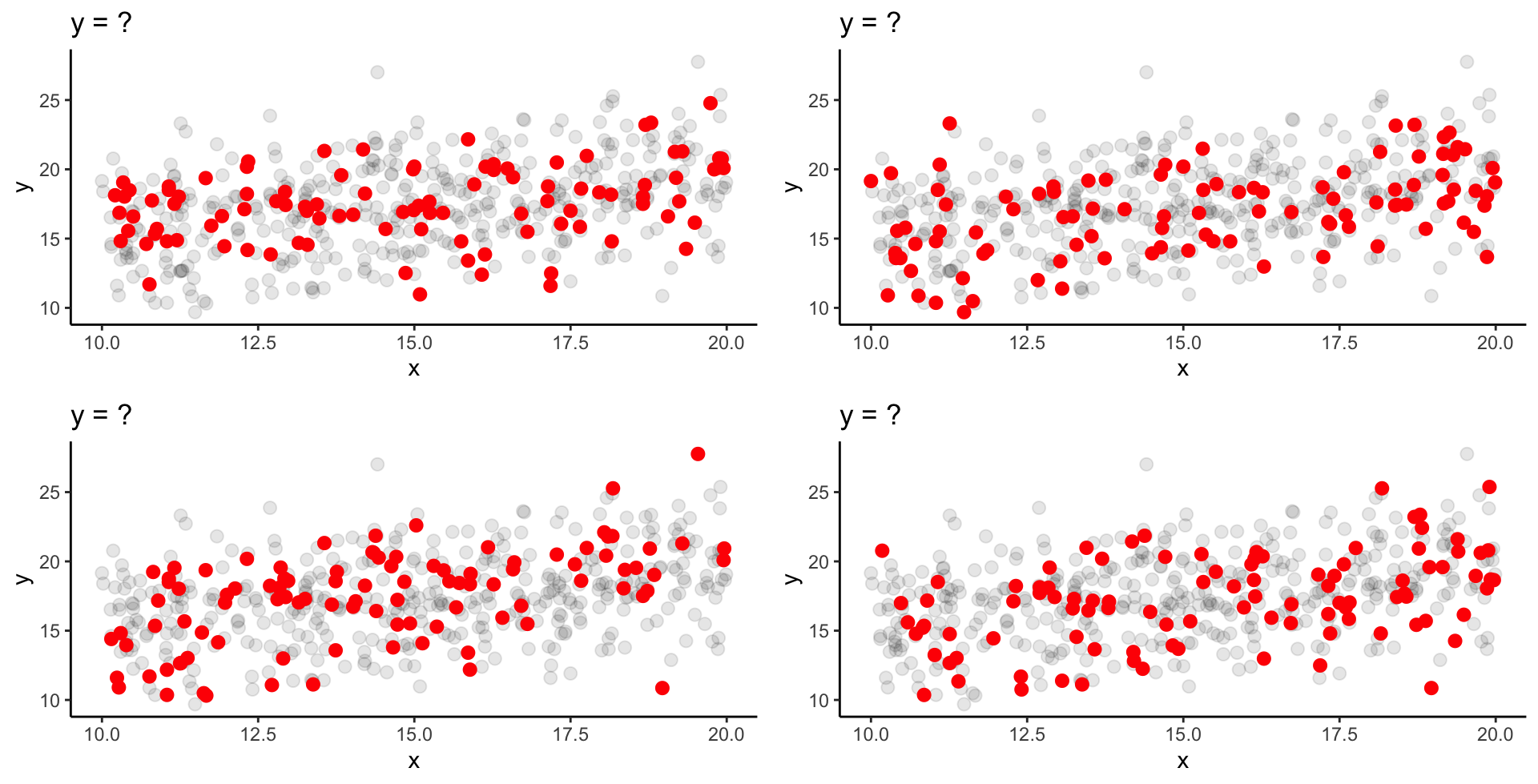
Wir steigern nun die Probengröße auf 100 Fische!
Starke Streuung & N = 100 | 2
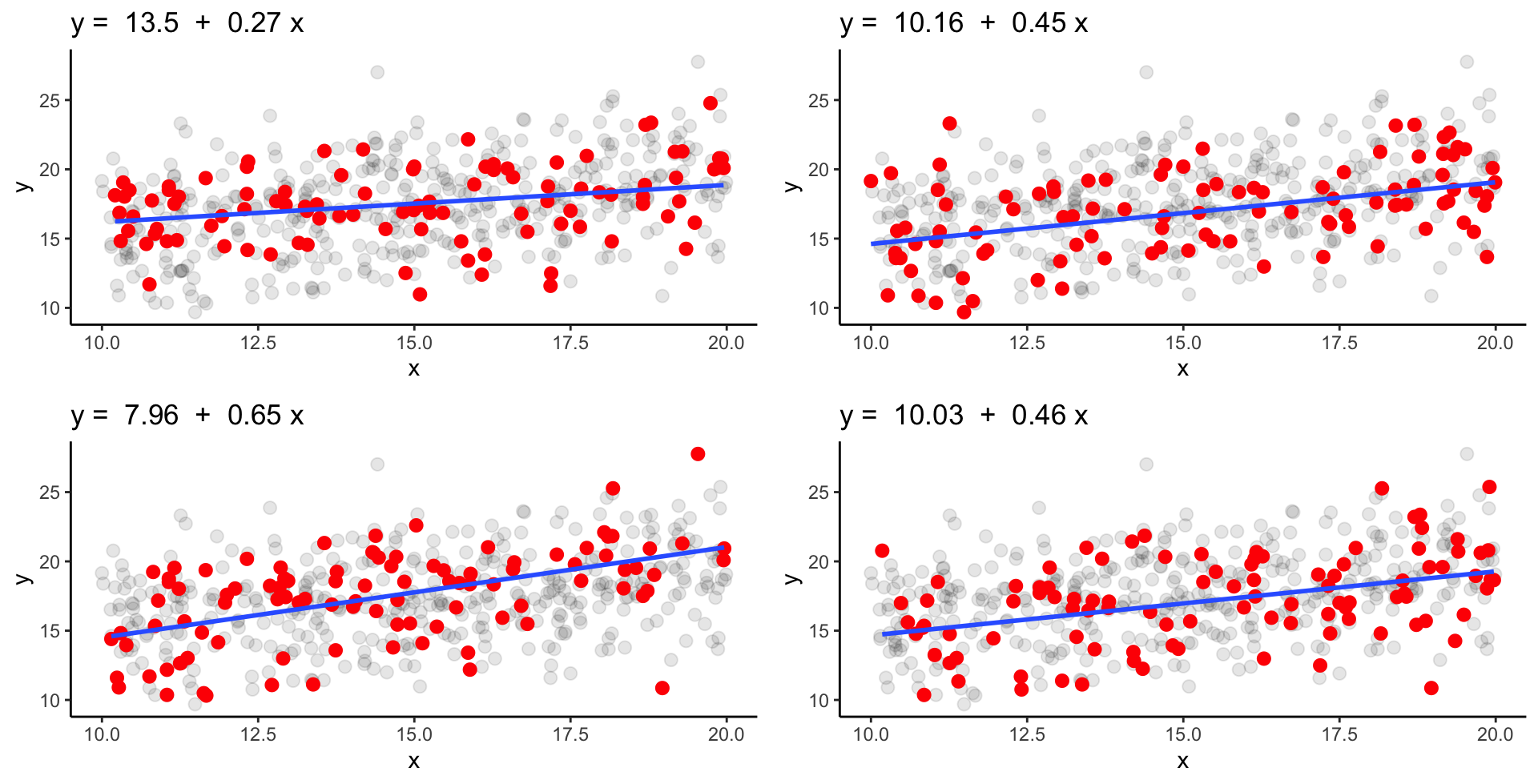
‘Wahre’ Parameter: \alpha = 11.27 und \beta = 0.41
Schwache Streuung & N = 10 | 1
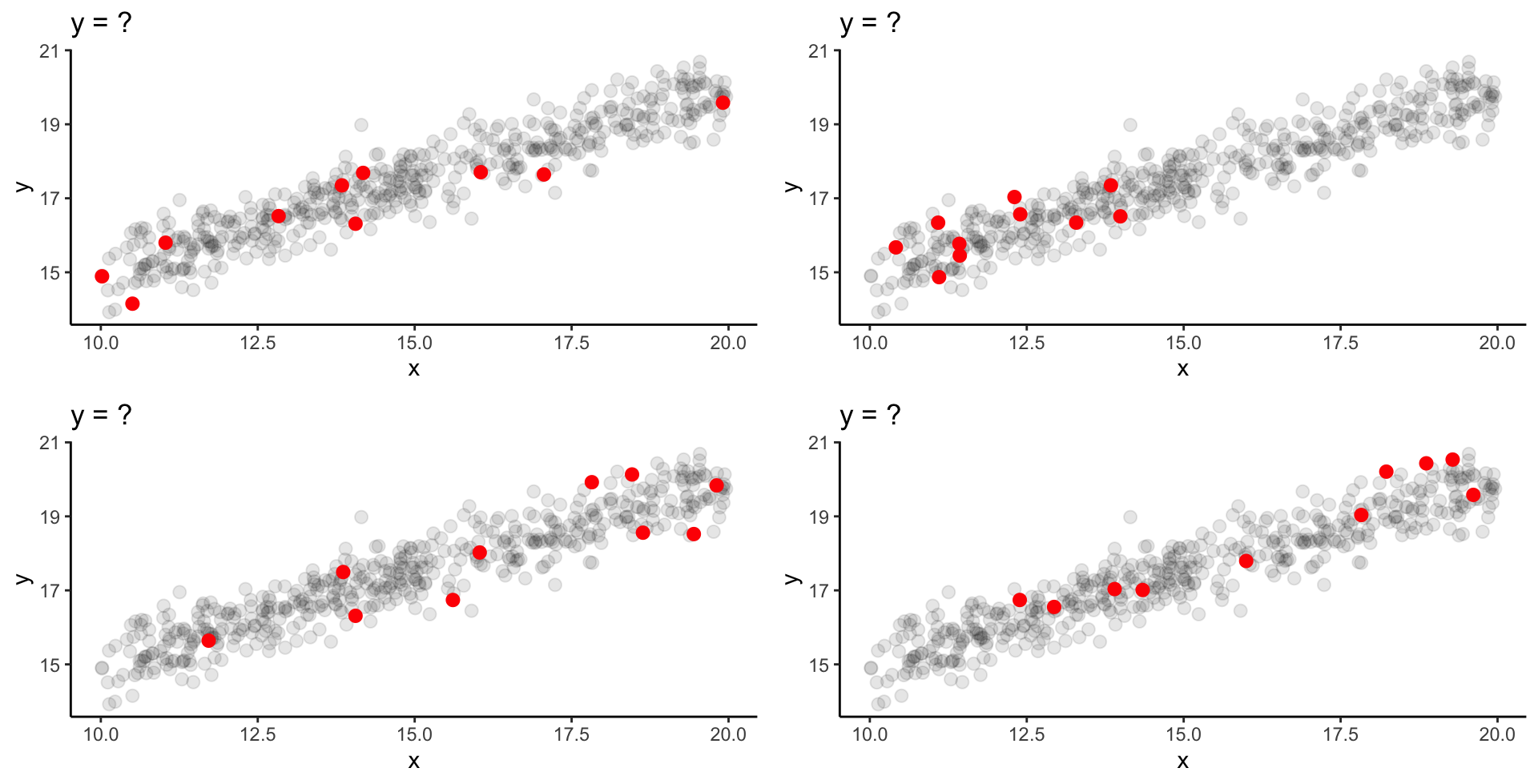
Wie ähnlich sind sich die geschätzten Koeffizienten bei schwacher Streuung und einem Stichprobenumfang von 10 Fischen?
Schwache Streuung & N = 10 | 2
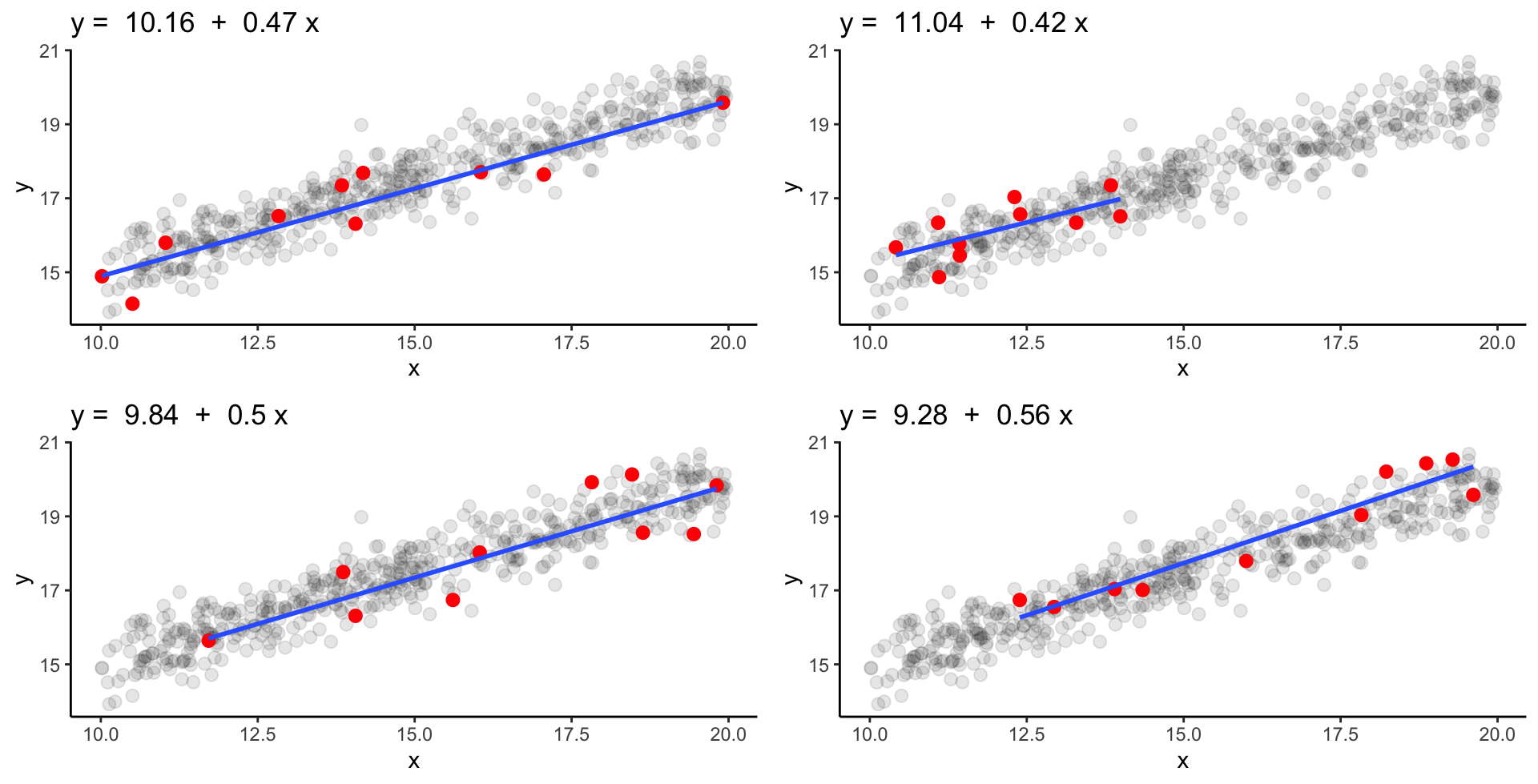
‘Wahre’ Parameter: \alpha = 10.04 und \beta = 0.50
Schwache Streuung & N = 100 | 1
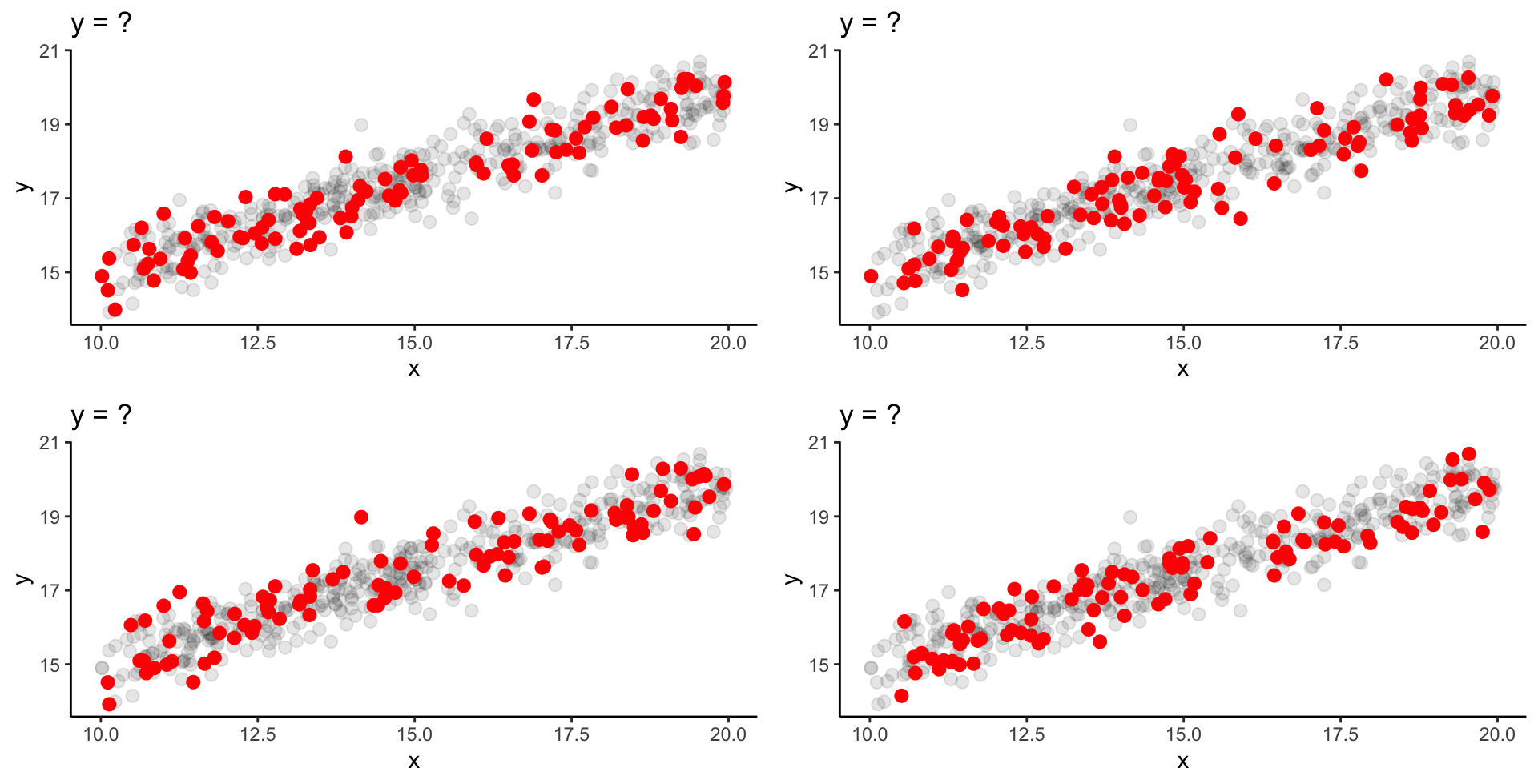
Wir steigern wieder die Probengröße auf 100 Fische!
Schwache Streuung & N = 100 | 2
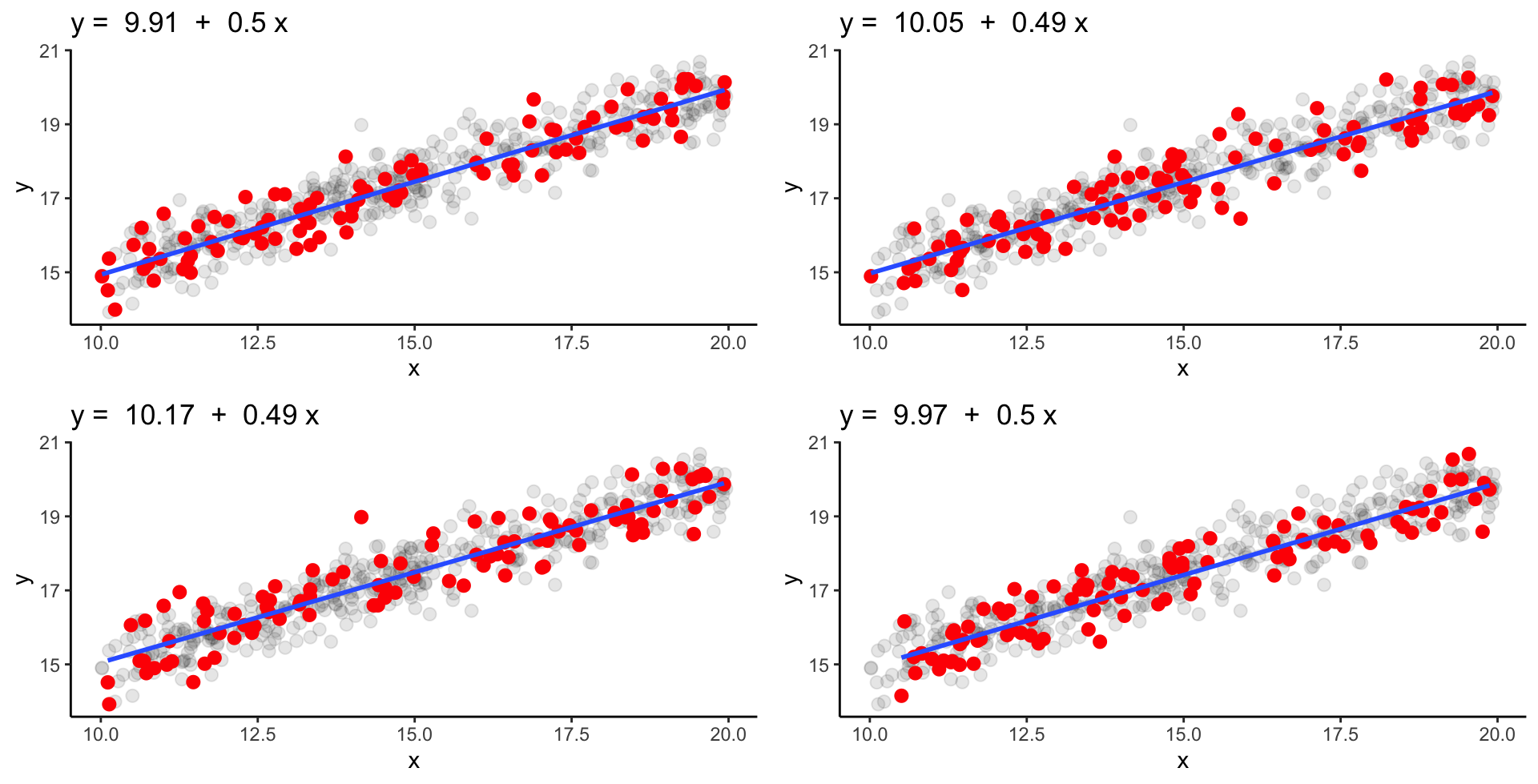
‘Wahre’ Parameter: \alpha = 10.04 und \beta = 0.50
Maß der Genauigkeit der geschätzten Koeffizienten
Die Unsicherheit der geschätzten Steigung und Achsenabschnitt
- steigt mit zunehmender Varianz und abnehmender Probengröße
- ist größer wenn die Spanne der Werte klein ist (gemessen als SS_{X})
Standardfehler des Achsenabschnitts und der Steigung
s_{\bar{a}}=\sqrt{\frac{MS_{Residual}\sum x_i^2}{n*SS_x}}=\sqrt{\frac{\frac{\sum(y_i-\hat{y_i})}{n-2}\sum x_i^2}{n*\sum(x_i-\bar{x})^2}}
s_{\bar{b}}=\sqrt{\frac{MS_{Residual}}{SS_x}}=\sqrt{\frac{\frac{\sum(y_i-\hat{y_i})}{n-2}}{\sum(x_i-\bar{x})^2}}
Varianzzerlegung in linearen Modellen
Zur Erinnerung
Die Gesamtstreuung (SS_Y oder SS_{Gesamt}) kann in 2 Komponenten zerlegt werden:
erklärbare Streuung = SS_{Regression} + nicht erklärbare Streuung = SS_{Residuen}
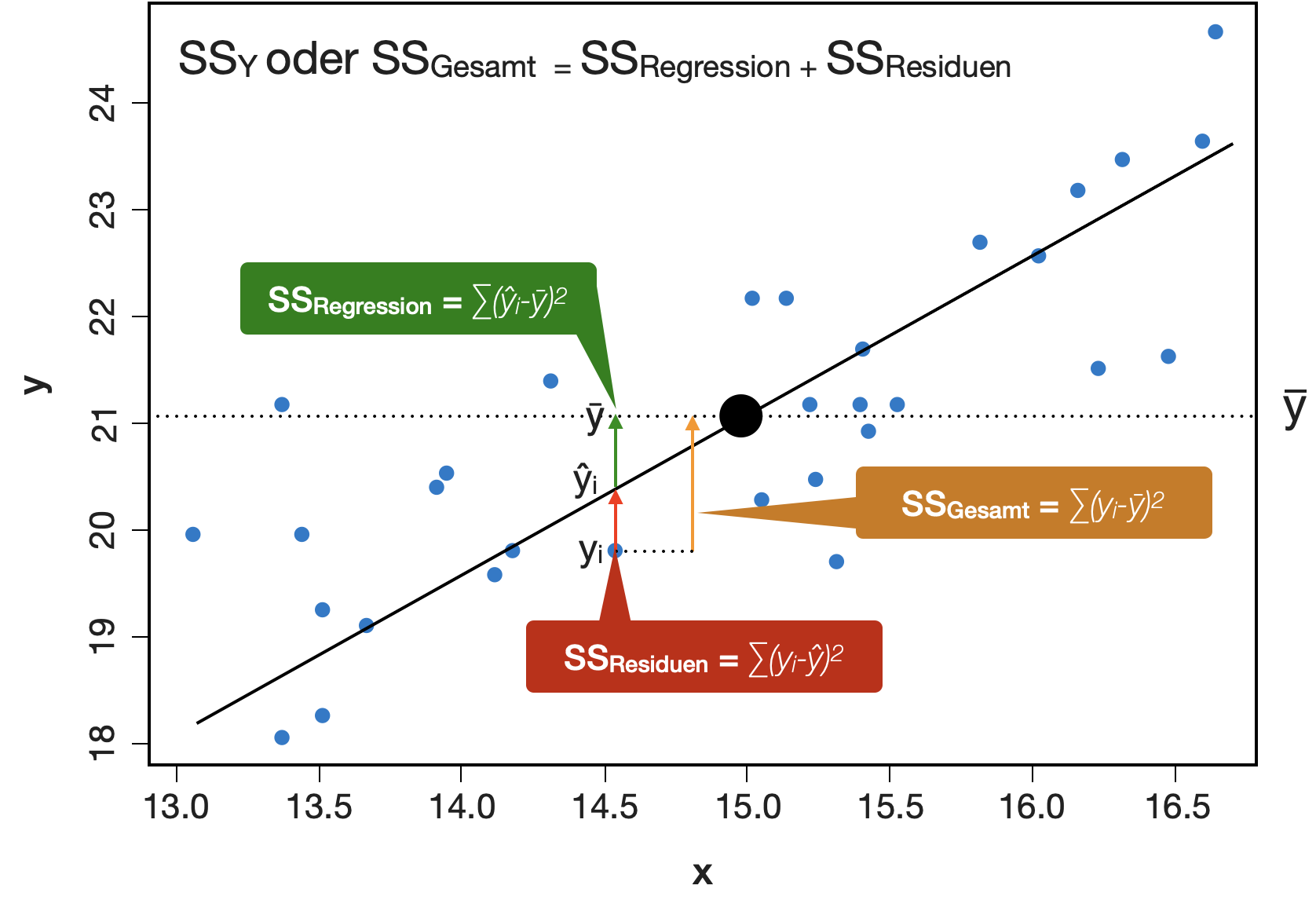
Was sind die Standardfehler im Daphnia-Modell?
Call:
lm(formula = offspring ~ length, data = daphnia)
Residuals:
Min 1Q Median 3Q Max
-18.12 -4.77 0.26 4.37 19.77
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -25.53847 2.43119 -10.5 <2e-16 ***
length 0.02329 0.00133 17.5 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.51 on 601 degrees of freedom
Multiple R-squared: 0.337, Adjusted R-squared: 0.336
F-statistic: 305 on 1 and 601 DF, p-value: <2e-16→ Punktschätzung für den Achsenabschnitt: -25.5 ± 2.43
→ Punktschätzung für die Steigung: 0.023 ± 0.001

Konfidenzintervalle der Koeffizienten
![]()
- Konfidenzintervalle kann man nicht nur für Mittelwerte oder Varianzen berechnen, auch für Regressionskoeffizienten.
- Berechnung basiert auf der t-Verteilung:
a <- -25.53847; b <- 0.02329
a_se <- 2.43119; b_se <- 0.00133
a_ci <- a_se * qt(p = 0.975, df = 603)
b_ci <- b_se * qt(p = 0.975, df = 603)
mat <- matrix(c(a-a_ci, a+a_ci, b-b_ci, b+b_ci), nrow = 2, byrow = TRUE)
rownames(mat) <- c("(Intercept)", "Sepal.Length")
colnames(mat) <- c("2.5%", "97.5%")
mat 2.5% 97.5%
(Intercept) -30.3131 -20.7638
Sepal.Length 0.0207 0.0259- Mit 95%iger Wahrscheinlichkeit liegt
- \alpha zwischen -30.3 und -20.8 und
- \beta zwischen 0.021 und 0.026
- Beide KI schließen nicht die Null mit ein → wir können davon ausgehen, dass \alpha \neq 0 und \beta \neq 0.
Signifikanztest der Koeffizienten
![]()
- Die Schätzungen der Koeffizienten basierend auf der Stichprobe weichen immer von Null ab.
- Ob dies Zufall ist oder nicht kann mit einem t-Test jeweils geprüft werden:
- H_0:~\alpha = 0, d.h. die Regressionsgerade geht durch den Ursprung.
- H_0:~\beta = 0, d.h. der Mittelwert ist für die Schätzung ebenso geeignet wie die Regressionsgerade.
Die Teststatistik t bei der Regression ist einfach nur der Quotient aus dem Schätzwert und seinem Standardfehler und folgt einer t-Verteilung:
- t_a = \frac{a}{s_{\bar{a}}} = \frac{-25.53847}{2.43119} = -10.5
- t_b=\frac{b}{s_{\bar{b}}} = \frac{0.02329}{0.00133} = 17.5
(Intercept)
-10.5 length
17.5 Testergebnisse im summary() Output
Call:
lm(formula = offspring ~ length, data = daphnia)
Residuals:
Min 1Q Median 3Q Max
-18.12 -4.77 0.26 4.37 19.77
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -25.53847 2.43119 -10.5 <2e-16 ***
length 0.02329 0.00133 17.5 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.51 on 601 degrees of freedom
Multiple R-squared: 0.337, Adjusted R-squared: 0.336
F-statistic: 305 on 1 and 601 DF, p-value: <2e-16
Interpretation der p-Werte
Wenn ein p-Wert sehr niedrig ist ( < 0.05), bedeutet das, dass
- die wahren \alpha und \beta Werte nicht 0 sind und wir unsere H0 ablehnen können.
- wir eine ungewöhnliche Stichprobe haben.
- unsere Annahmen für das Modell falsch sind → wir müssen daher immer anschließend eine Modelldiagnostik durchführen!
Wie gut ist das Modell?
Zur Erinnerung: das Bestimmtheitsmaß R^2
Die statistische Kenngröße R^2 ist ein Maß für den Anteil der Variabilität in y, welcher durch das lineare Modell erklärt werden kann:
R^2 = \frac{SS_{Regression}}{SS_{Gesamt}} = \frac{\sum(\hat{y}_i-\bar{y})^2}{\sum(y_i-\bar{y})^2} 1 \geq R^2 \geq 0
- Werte nahe 1 weisen auf eine sehr gute Beschreibung der Daten hin.
- Werte nahe 0 weisen auf eine sehr hohe Streuung der Daten um die Gerade hin.
- Bei R^2=1 lägen alle Datenwerte exakt auf der Geraden.
- In der Ökologie wird bereits ein R^2 von 0.5 bzw. 50% als sehr gut erachtet.
- R^2 stellt auch das Quadrat des Korrelationskoeffizienten r dar.
Das Bestimmtheitsmaß R^2 im Output
Call:
lm(formula = offspring ~ length, data = daphnia)
Residuals:
Min 1Q Median 3Q Max
-18.12 -4.77 0.26 4.37 19.77
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -25.53847 2.43119 -10.5 <2e-16 ***
length 0.02329 0.00133 17.5 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.51 on 601 degrees of freedom
Multiple R-squared: 0.337, Adjusted R-squared: 0.336
F-statistic: 305 on 1 and 601 DF, p-value: <2e-16
Modellvalidierung

Voraussetzungen bzw. Annahmen für lineare Modelle
- Linearität der Beziehung
- Homogenität / homogene Varianz
- Normalität / Normalverteilung
- Unabhängigkeit der Beobachtungen
Wie können die Annahmen überprüft werden?
VOR dem Modellieren
- Linearität:
- Streudiagramm mit X vs. Y
- Varianzhomogenität:
- Streudiagramm mit X vs. Y
- Normalität:
- Histogramm von Y
- Shapiro-Wilk-Test mit Y
NACH dem Modellieren
Modellvalidierung mittels sog. Diagnostikplots mit den Residuen:
- Varianzhomogenität:
- Streudiagramm mit Residuen vs. vorhergesagte Y-Werte
- Normalität:
- Histogramm oder QQ-Plot
- Shapiro-Wilk-Test
- Unabhängigkeit:
- Zeitserien: Diagramm der ACF Funktion
- Räumliche Daten: Variogramm
Normalität und Varianzhomogenität | 1
VOR dem Modellieren: Annahmen sollen entlang der Achsen erfüllt sein
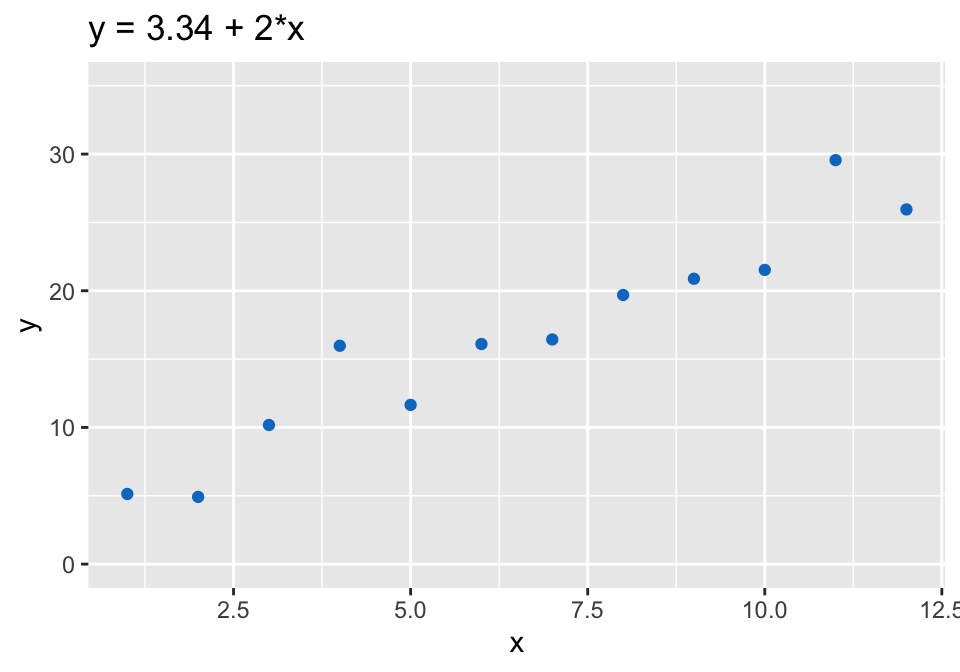
→ Überprüfung beider Annahmen anhand einer Exploration der y Variable schwierig
→ Was aber, wenn es pro X-Wert 50 Beobachtungen gäbe?
Normalität und Varianzhomogenität | 2
VOR dem Modellieren: Annahmen sollen entlang der Achsen erfüllt sein
→ bei Replikation offensichtlicher:
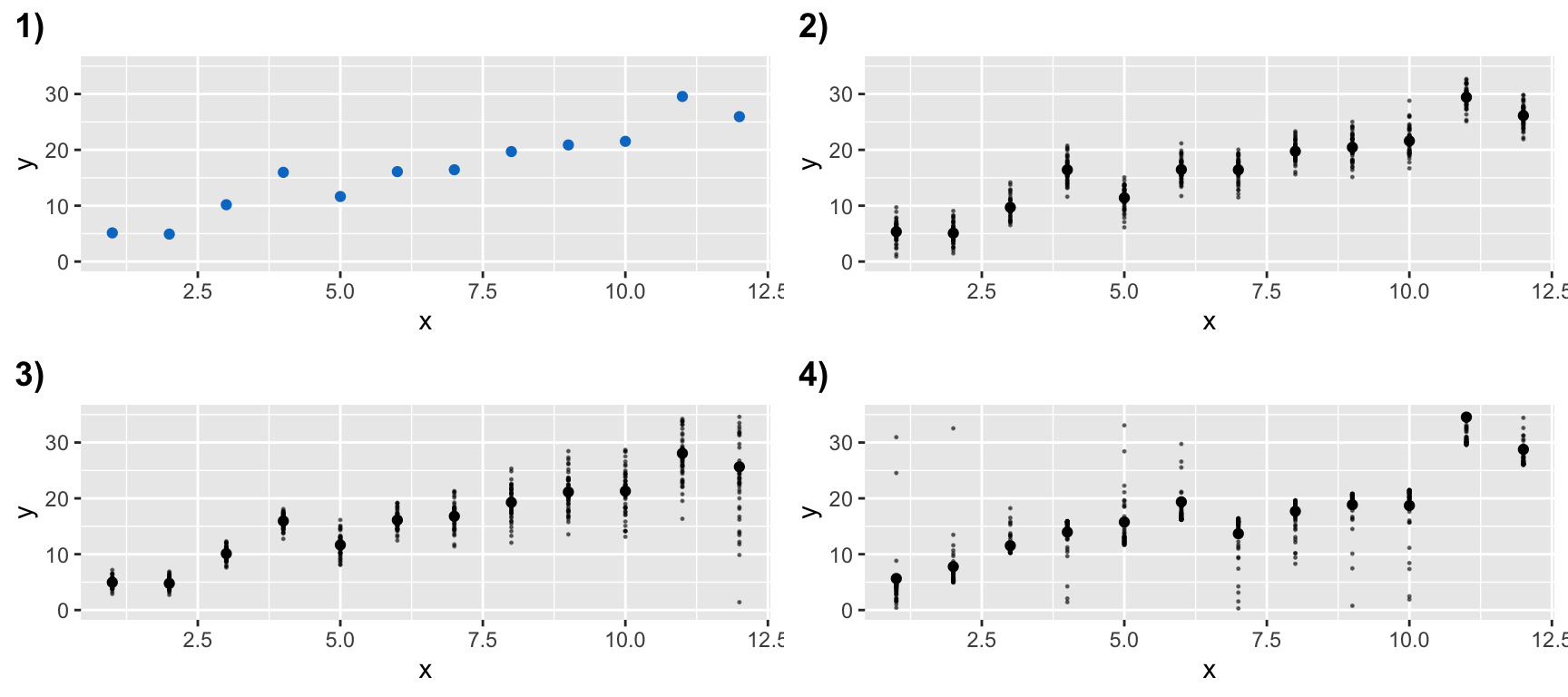
Wo sind die jeweils 50 Beobachtung bei x = 2,3,4… normal verteilt sein und die Varianzen zwischen den versch. X-Werten homogen?
Normalität und Varianzhomogenität | 3
VOR dem Modellieren: Annahmen sollen entlang der Achsen erfüllt sein
→ bei Replikation offensichtlicher:
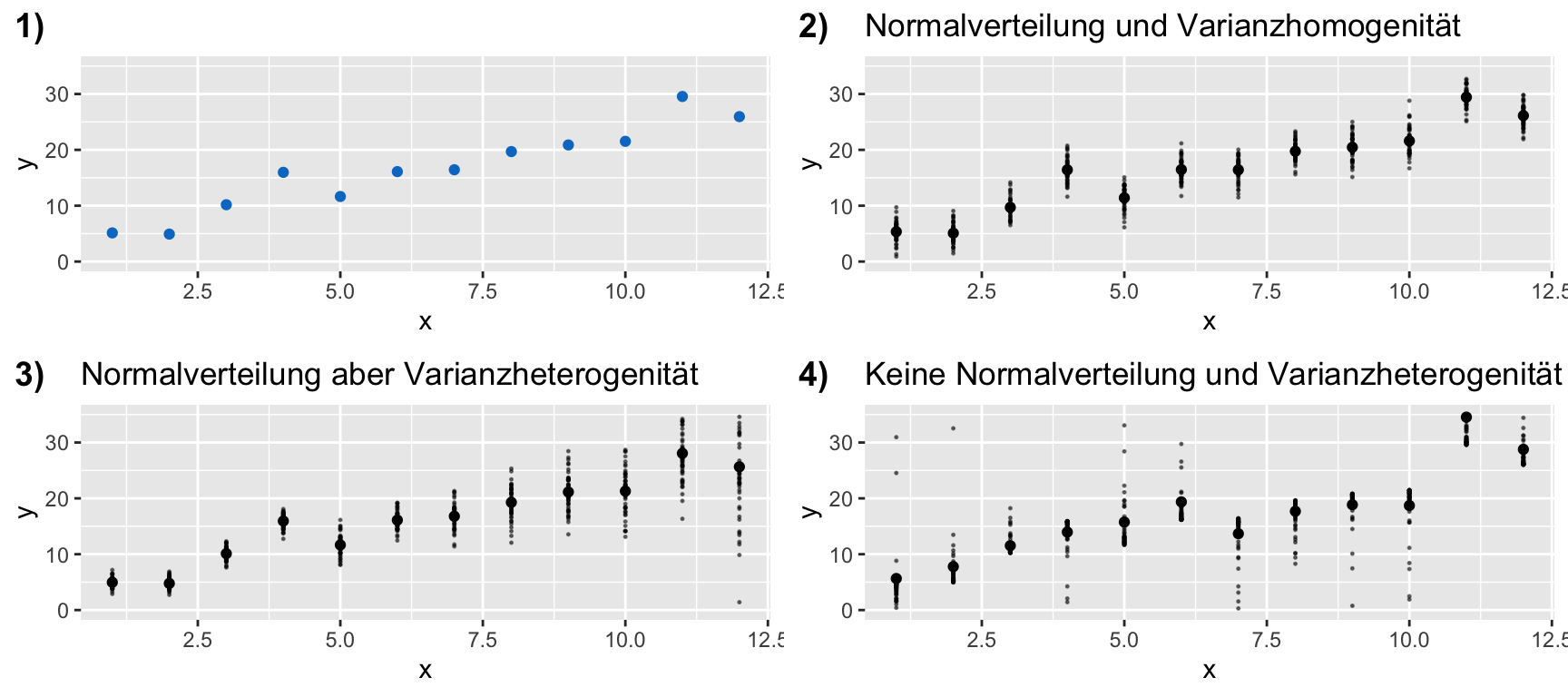
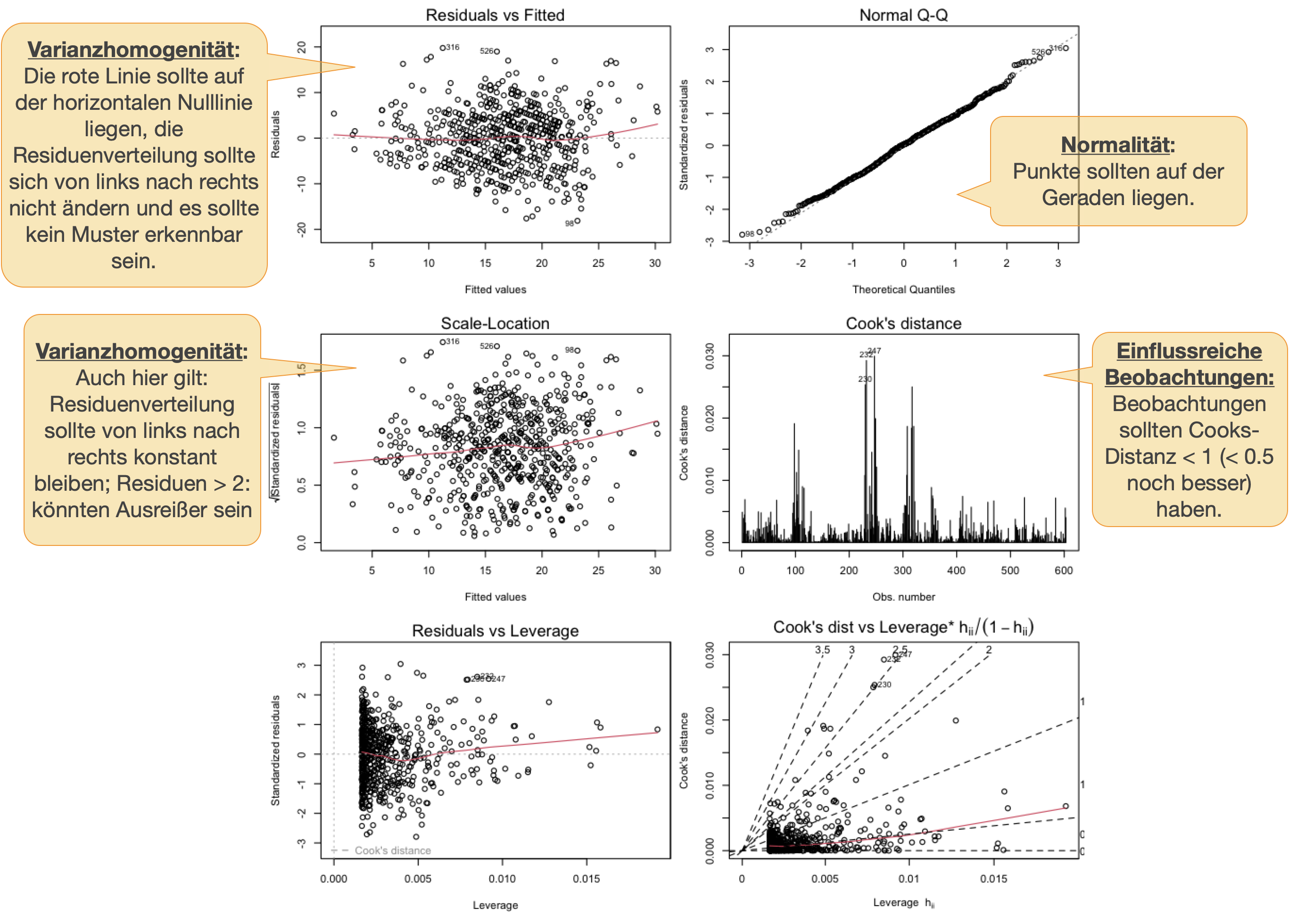
Standardgrafiken zur Modellvalidierung
![]()
Gewöhnliche vs standardisierte Residuen
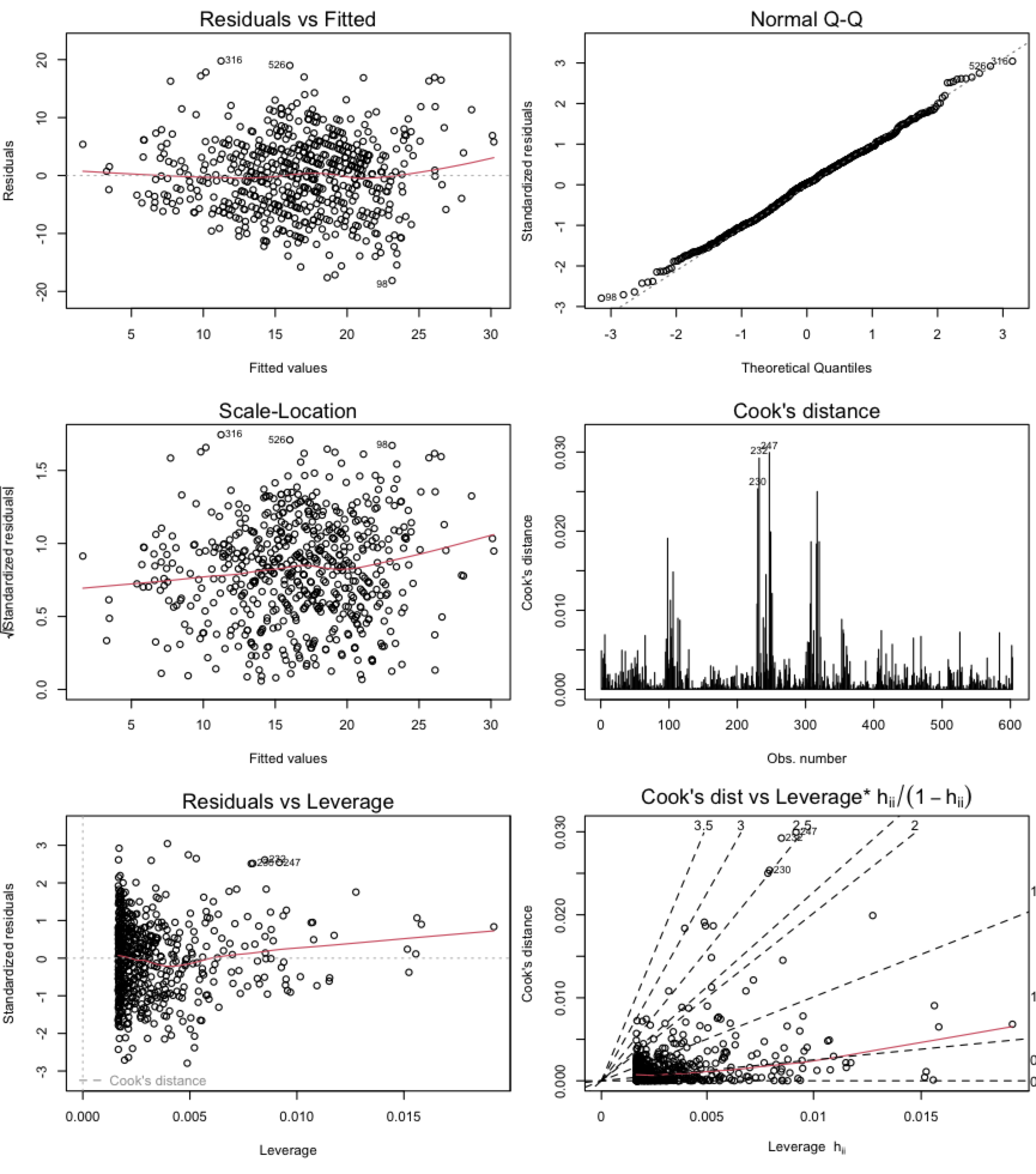
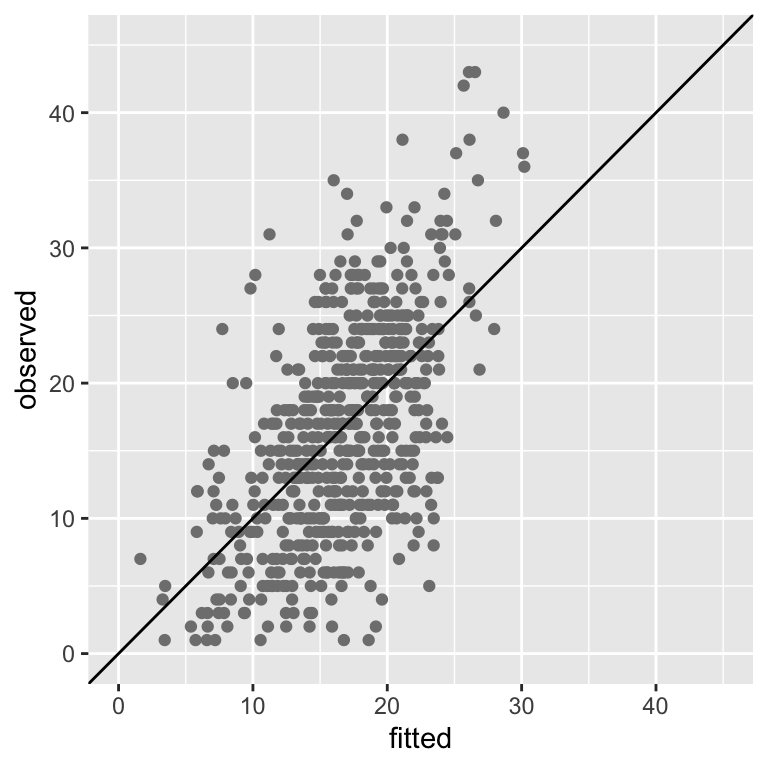
- Gewöhnliche Residuen (e_i):
- beobachtete Werte - vorhergesagte Werte (‘observed – fitted’)
- Standardisierte Residuen (e_{stand.}):
- Residuum dividiert durch seine Standardabweichung: e_{stand.} = \frac{e_{i}}{\sqrt{MS_{Residual}*(1-h_{i})}}
- wobei h_{i} = leverage der einzelnen Beobachtungen i;
- MS_{Residual} = Mittlere Summenquadrate der Residuen
- werden als normalverteilt angenommen mit einem Mittelwert von 0 und einer Varianz von 1.
- große Residuenwerte (>4) bedeuten eine schlechte Anpassung des Regressionsmodels.
- Residuum dividiert durch seine Standardabweichung: e_{stand.} = \frac{e_{i}}{\sqrt{MS_{Residual}*(1-h_{i})}}
Ausreißer/Einflussreiche Beobachtungen | 1
Leverage und Cook’s Distanz

- ‘Leverage’ h: ein Werkzeug, dass Extremwerte der erklärenden Variable identifiziert, welche potentiell auch das Regressionsergebnis beeinflussen könnten.
- Cook’s Distanz D: das Maß für zu einflussreiche Datenpunkte. Identifiziert einzelne Beobachtungen, die alle Regressionsparameter beeinflussen. Es berechnet eine Teststatistik D, die die Veränderung aller Regressionsparameter misst, wenn eine Beobachtung ausgeschlossen wird.
- D > 0.5 kritisch
- D > 1.0 sehr kritisch
→ Es ist einfacher den Ausschluss beeinflussender Datenpunkte zu rechtfertigen, wenn eine große Cook’s Distanz und eine große Leverage für den Datenpunkt vorliegt.
Ausreißer/Einflussreiche Beobachtungen | 2
Leverage und Cook’s Distanz
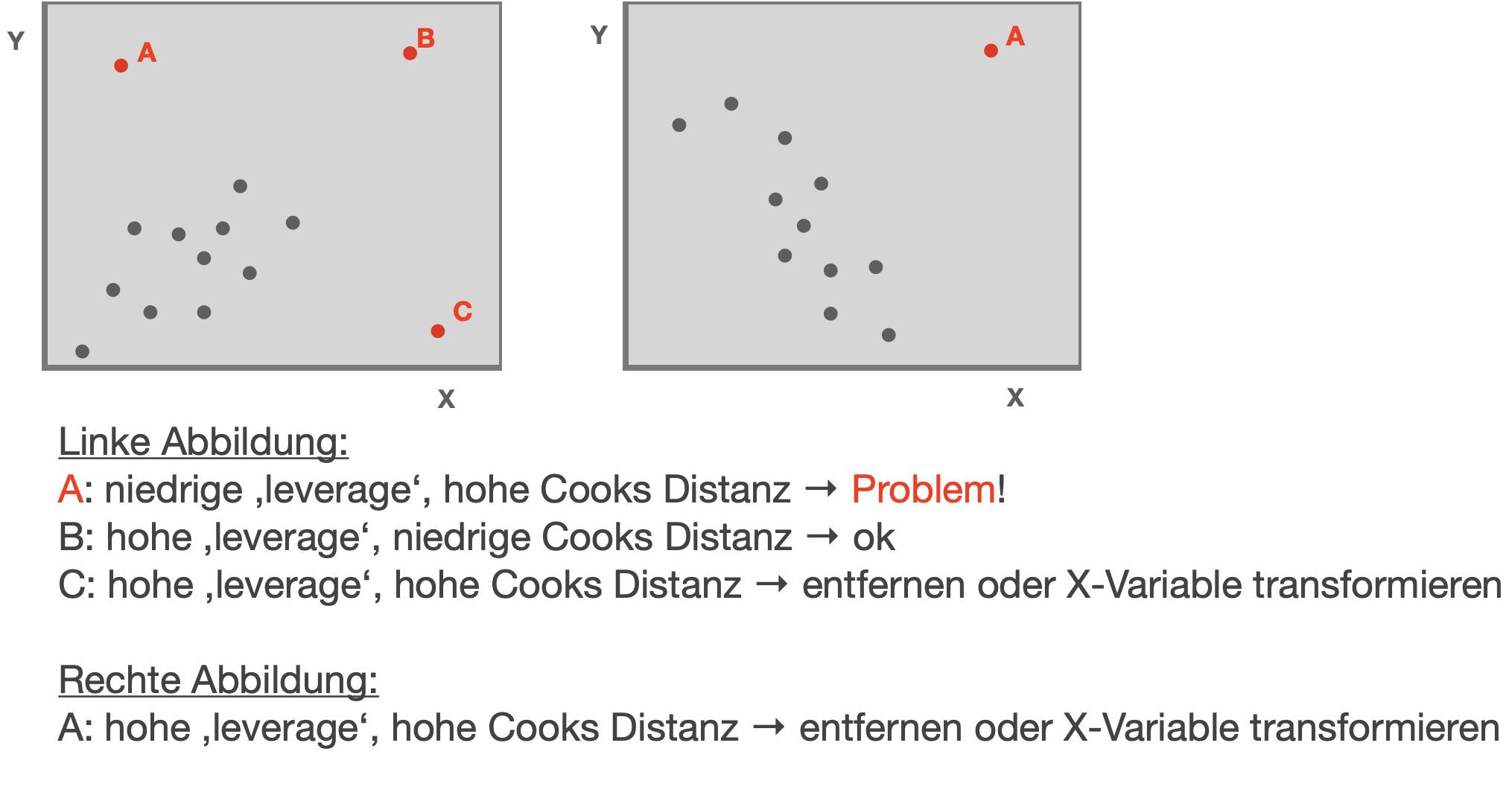
Modifizierte Abb. aus: Zuur et al. (2007)
Funktionen zur Ausgabe der …
Residuen
residuals()→ gibt einen Vektor mit den gewöhnlichen Residuen ausrstandard(model)→ gibt einen Vektor mit den standardisierten Residuen aus
Vorhergesagten Werte
fitted(model)→ gibt einen Vektor mit den angepassten Werte zurück, die vom Modell für die Werte der erklärenden Variablen vorhergesagt werdenpredict(model)→ verwendet Informationen aus dem angepassten Modell, um eine Glättungsfunktion für die Darstellung einer Linie im Streudiagramm zu erstellen. Der Funktion kann ein neuer data frame mit Sequenzen von Werten aller X Variablen, die im Modell sind, übergeben werden (Argumentnewdata).
Weitere Diagramme zur Modellvalidierung | 1
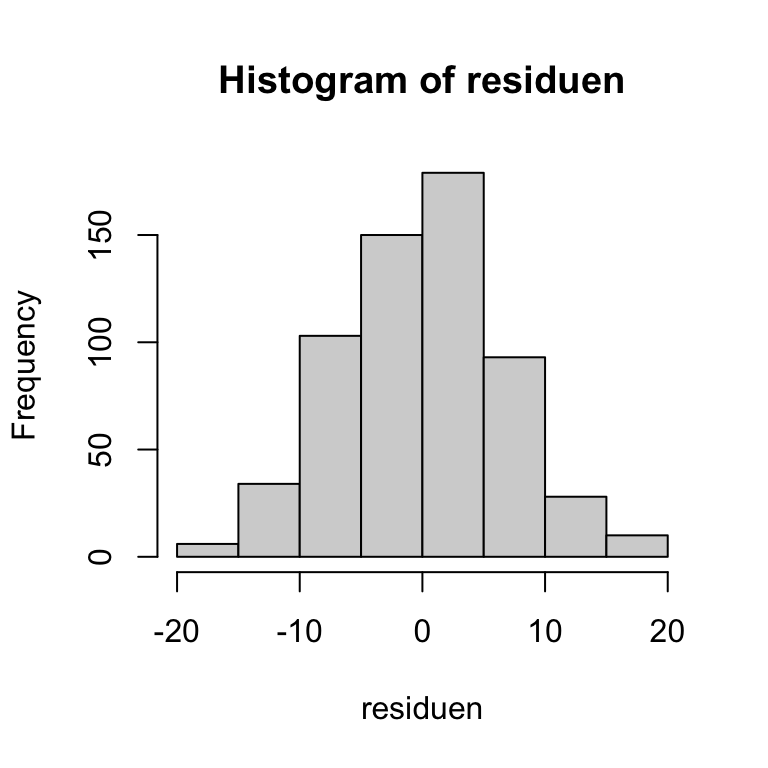
NACH dem Modellieren: Histogramm der Residuen und Shapiro-Wilk-Test
Nützlich, wenn Plot 2 in der Standardgrafik schwer interpretierbar ist.
Shapiro-Wilk normality test
data: residuen
W = 1, p-value = 0.3→ Hier ist die Voraussetzung der Normalität nun gegeben.
Weitere Diagramme zur Modellvalidierung | 2
Visualisierung der linearen Regression
Your turn …
![]()
03:00
Quiz | Verteilung & Modellspezifikation
![]()
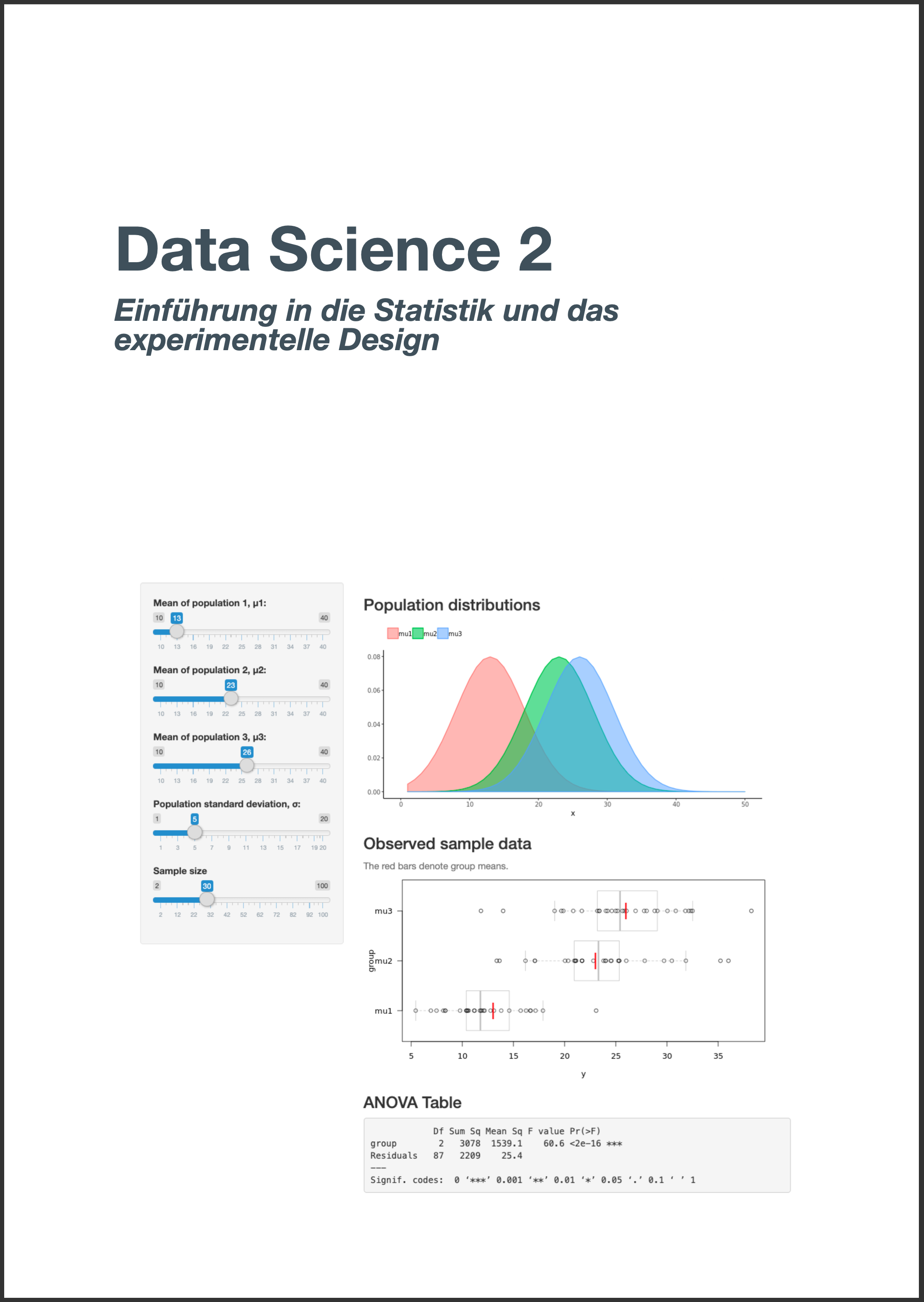
Erkunde die Shiny App auf der folgenden Folie und beantworte folgende Fragen:
Quiz | Verteilung & Modellspezifikation
![]()
Shiny App
Link zur Shiny-App: teaching-stats/diagnostics/simple-linear-regression/
Übungsaufgaben
![]()
Übungstag 5
Korrelation und Regression
![]()
- Aufgaben:
- 5.1 Hausaufgabe zur Vorbereitung: Transformation
- 5.2 Korrelation: Pearsons Produkt-Moment Korrelationskoeffizient
- 5.3 Regression - Einfluss von Muschelbänken auf Wirbellosendichte
- 5.4 Nachbereitung Fallstudie: Frage 3
- R Notebook-Skript:
- DS2_05_Uebungen_Korrelation_Regression.Rmd
Fragen?
Abschlussquiz
![]()

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de

Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.
Kurswebseite: Data Science 2