9-Korrelation & Transformation

Data Science 2

Saskia Otto

Universität Hamburg, IMF

Sommersemester 2024

Lernziele

Nach Abschluss dieser VL und Übung..

  • kennen Sie den Zusammenhang zwischen Kovarianz und Korrelation.
  • können Sie den parametrischen Pearson-Produkt-Moment-Korrelationskoeffizienten und die beiden nicht-parametrischen Spearman Rangkorrelationskoeffizient und Kendall’s Tau in R berechnen.
  • wissen Sie, welcher dieser Koeffizienten bei Ihren Daten der passende ist.
  • können Sie die R Funktion zum Testen der Nullhypothese \rho = 0 anwenden.
  • können Sie viele Korrelationen zusammen visualisieren.
  • kennen Sie die Powertransformation und die Box-Cox-Transformation.
  • wissen Sie, wie Sie die richtige Transformation zur Datennormalisierung, Varianzhomogenisierung und Linearisierung auswählen.

Auf Zusammenhänge testen

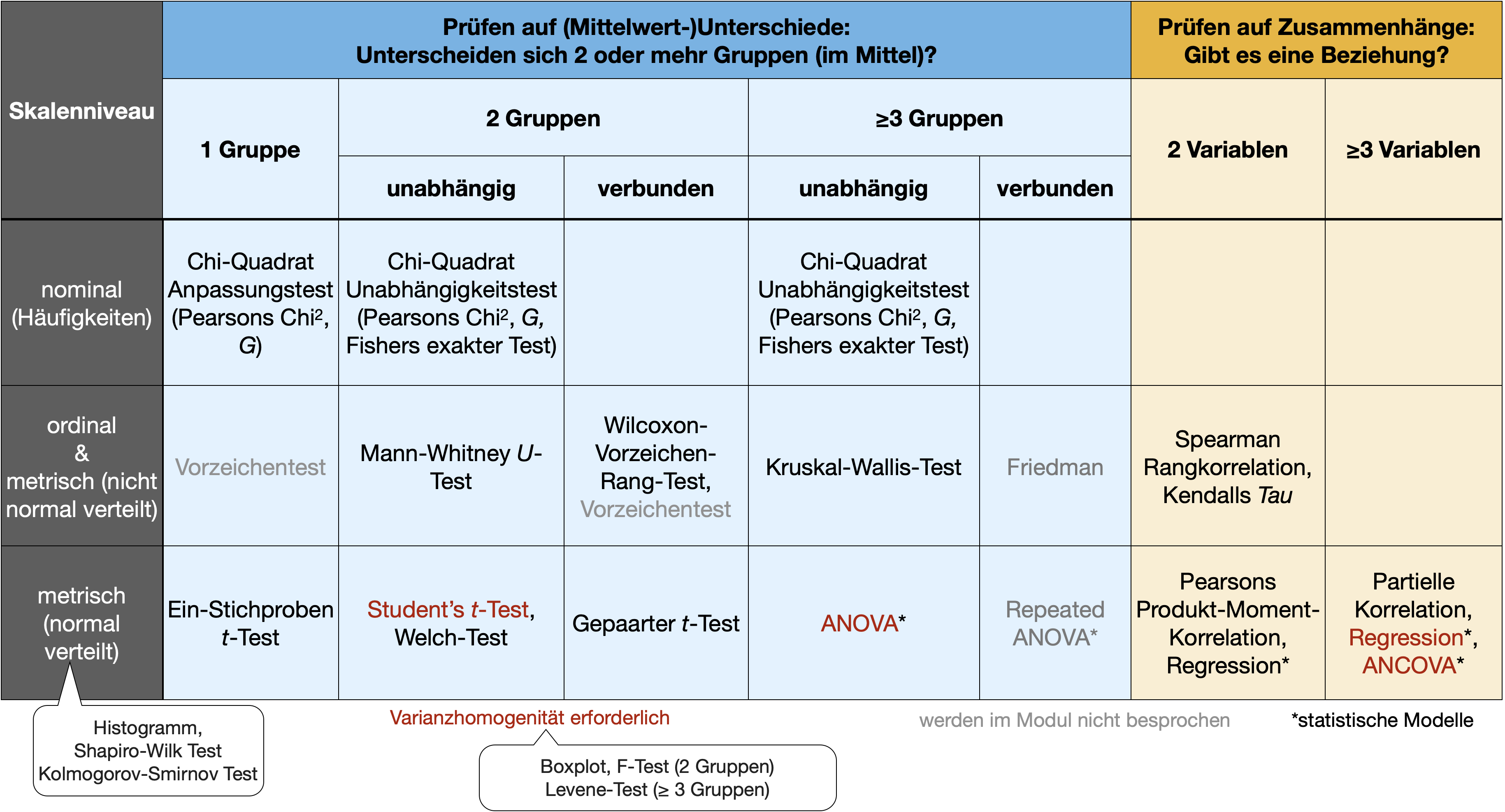
Zur Erinnerung aus DS1 …

Korrelation

  • Prüfen von Beziehungen ohne Kausalität.
  • Das Skalenniveau kann ordinal oder metrisch sein.
  • Beide Variablen sind zufällige Variablen, es wird keine manipuliert.
  • Je nach Skalenniveau und Verteilung wird der Korrelationstyp gewählt.

Regression

  • Prüfen von Beziehungen mit Kausalität.
  • Beide Variablen müssen metrisch sein.
  • Unterscheidet in
    • Abhängige oder Antwortvariable Y
    • Unabhängige oder erklärende Variable X; diese wird meist manipuliert.

Bivariate Beziehungen

Charakterisierung bivariater Beziehungen

  • Form (linear, monoton, nicht-linear, quadratisch)
  • Richtung (positiv, negativ)
  • Stärke (wie viel Streuung/Rauschen?)
  • Ausreißer

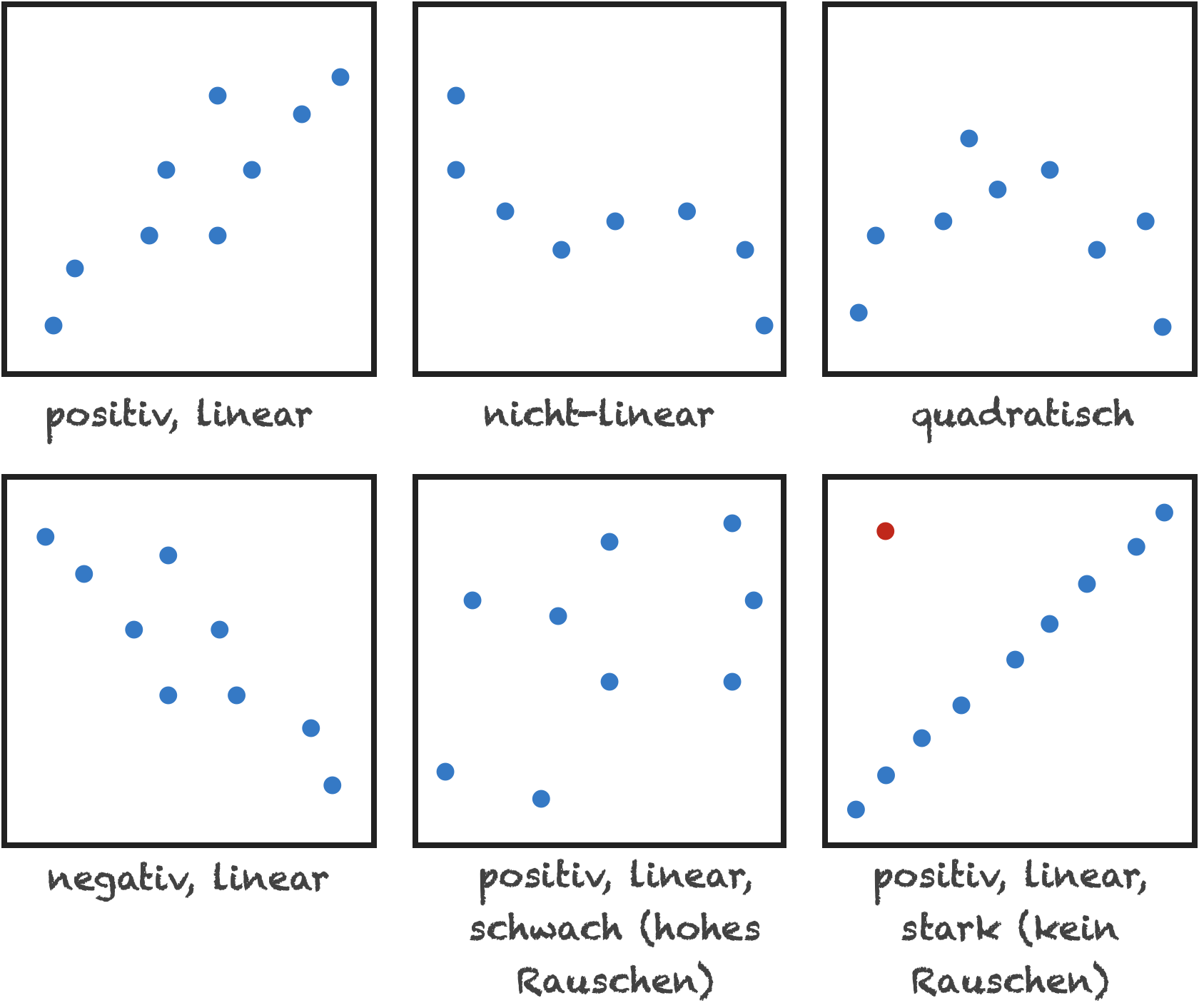
Die Form

  • Zur Berechnung der (Pearson) Korrelation ist eine lineare Beziehung erforderlich → oft nicht-linear!
  • Transformation einer oder beider Variablen kann die Beziehung linearisieren.

Darstellungsmöglichkeiten mit ggplot2

(ohne die Rohdaten zu transformieren):

  • scale_x_log10() und scale_y_log10() log-transformiert die X- und Y-Achse zur Basis 10.
  • coord_trans() transformiert die Koordinaten des Plots entsprechend der angegebenen Transformation.

Die Form | Streudiagramm der Rohdaten

MASS::mammals |>
ggplot(aes(x = body, y = brain)) + 
  geom_point()

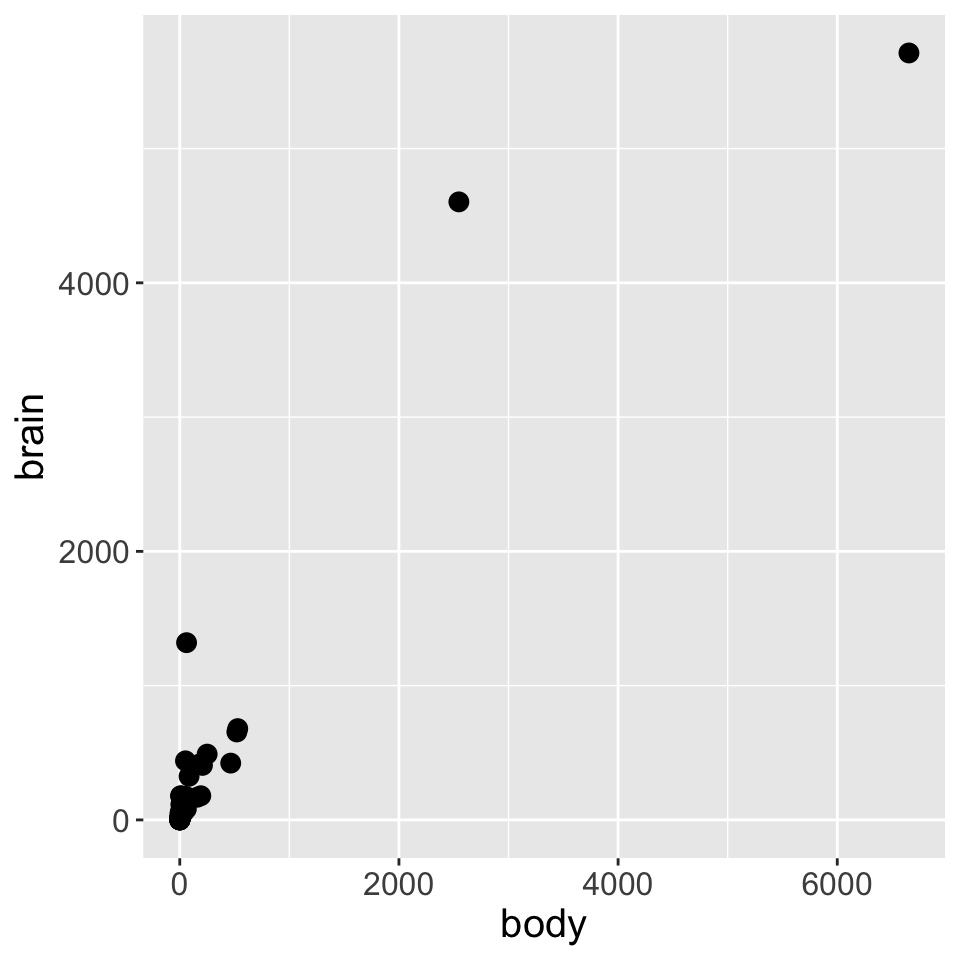
Hier ein Beispiel des möglichen Zusammenhangs zwischen dem Körpergewicht (in kg) und der Gehirnmasse (in g) von Säugetieren (Datensatz mammals aus dem Paket ‘MASS’).

Die Form | Streudiagramm mit scale_...

MASS::mammals |>
ggplot(aes(x = body, y = brain)) + 
  geom_point() +
  scale_x_log10() + 
  scale_y_log10()

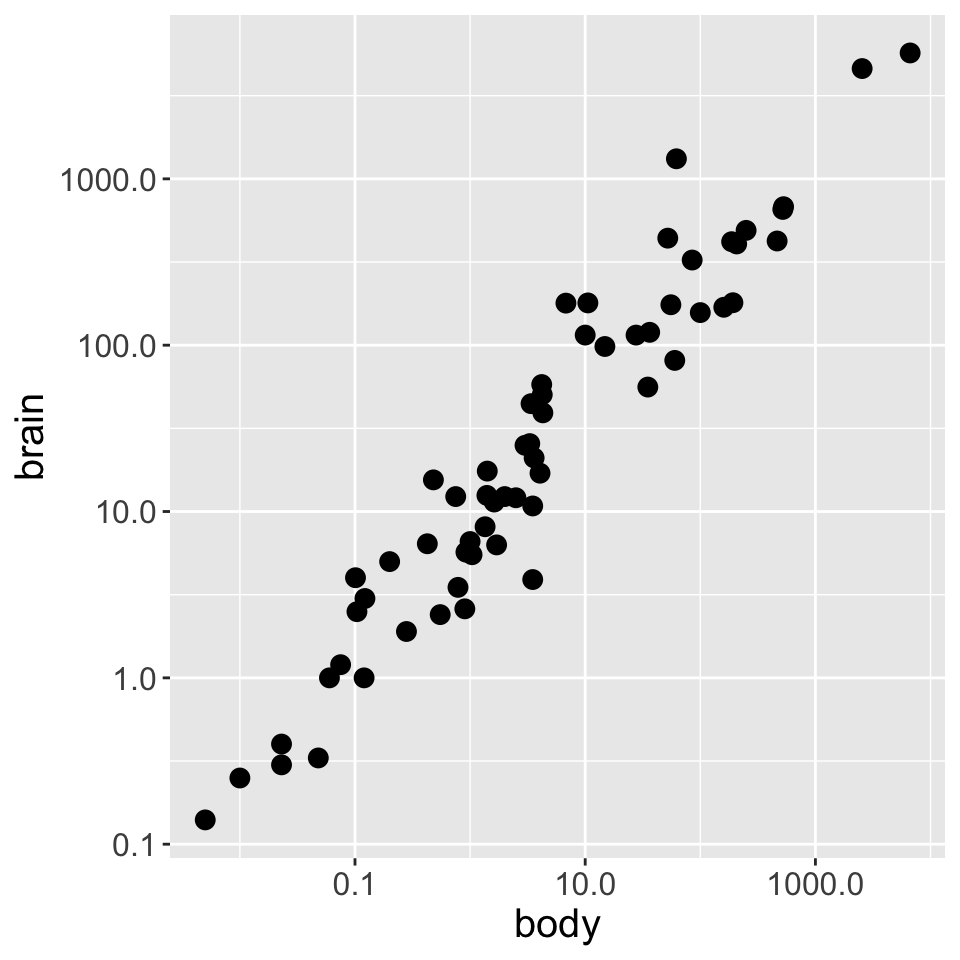
Hier ein Beispiel des möglichen Zusammenhangs zwischen dem Körpergewicht (in kg) und der Gehirnmasse (in g) von Säugetieren (Datensatz mammals aus dem Paket ‘MASS’).

Die Form | Streudiagramm mit coord_trans()

MASS::mammals |>
ggplot(aes(x = body, y = brain)) + 
  geom_point() +
  coord_trans(
    x = "log10", 
    y = "log10"
  )

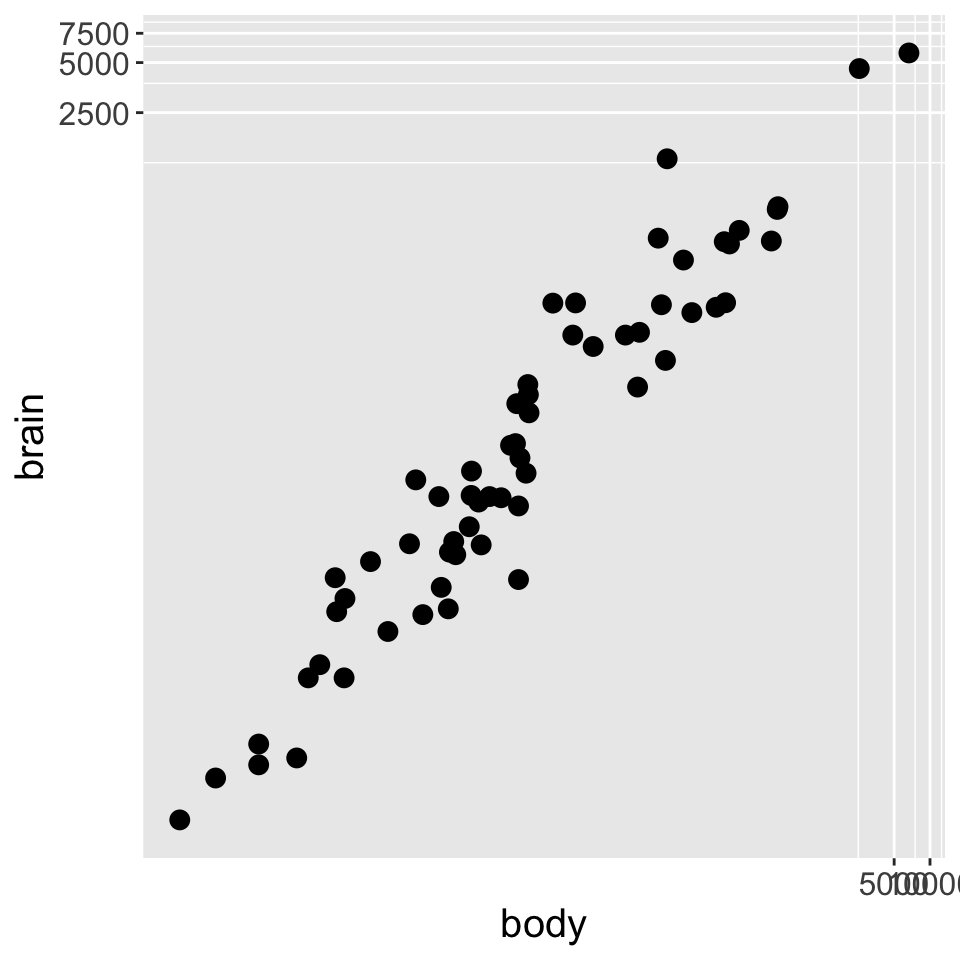
Hier ein Beispiel des möglichen Zusammenhangs zwischen dem Körpergewicht (in kg) und der Gehirnmasse (in g) von Säugetieren (Datensatz mammals aus dem Paket ‘MASS’).

Quantifizierung der Stärke und Richtung von bivariaten Beziehungen

  • Messgröße: Korrelationskoeffizient
  • Wertebereich: -1 bis +1
    • Das Vorzeichen gibt die Richtung der Beziehung an.
    • Der Betrag die Stärke
      • 0 = keine Korrelation
      • -1 = starke negative Korrelation
      • +1 starke positive Korrelation

→ Dies gilt allerdings nur bei linearen bzw. monotonen Zusammenhängen!

Streuungsparameter bei 1 vs. 2 Variablen

(korrigierte) Varianz von Y

s^{2} = \frac{1}{n-1}\sum\limits_{i=1}^{n}(y_{i} - \bar{y})^2 = \frac{1}{n-1}SS_Y

Kovarianz zwischen X und Y

Cov(x,y)=\frac{1}{n-1}\sum\limits_{i=1}^{n}(x_i- \bar{x})(y_i- \bar{y}) = \frac{1}{n-1}SS_{XY}

Kovarianz | Grafisch

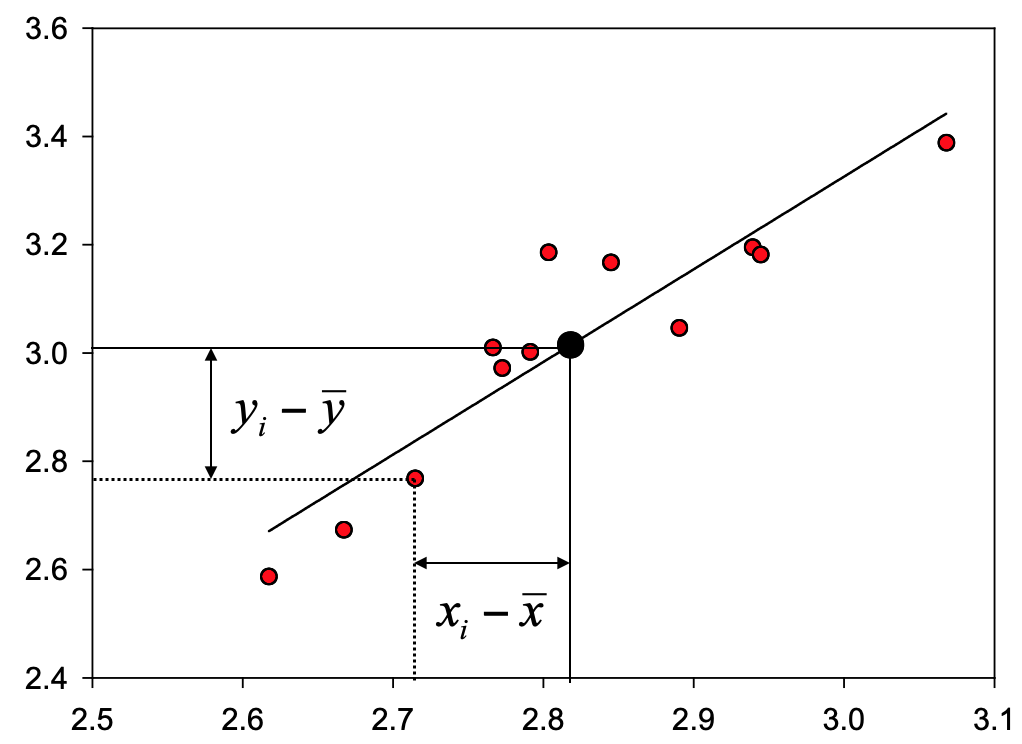
Standardisierung der Kovarianz

  • Die Kovarianz ist ein Maß für die Stärke einer linearen Beziehung
  • Einschränkung: absolute Größe hängt von den Einheiten der beiden Variablen ab.

Lösung: Maximale Kovarianz

  • Standardisierung der Kovarianz mit den beiden Standardabweichungen, so dass das Maß der Stärke zwischen -1 und +1 liegt:

\frac{Cov(x,y)}{Cov(x,y)_{max}} = \frac{Cov(x,y)}{s_x*s_y}

→ Pearson Produkt-Moment-Korrelationskoeffizient

Parametrischer Korrelationskoeffizient

Pearson Produkt-Moment-Korrelationskoeffizient \rho

  • Annahmen: Normalverteilung und Linearität
  • Der Korrelationskoeffizient r (bzw. \rho für die Population) wird durch das Verhältnis zwischen der Kovarianz und der maximalen Kovarianz quantifiziert:

r_{x,y} = \frac{Cov(x,y)}{Cov(x,y)_{max}} = \frac{\frac{1}{n-1}\sum\limits_{i=1}^{n}(x_i- \bar{x})(y_i- \bar{y})}{s_x*s_y}

  • r = \sqrt{R^2} → r ist die Quadratwurzel des “Bestimmtheitsmaßes” R^2
  • r = [-1,+1] → R^2 ist immer positiv, während r die Richtung des Zusammenhangs angibt!

Nichtparametrischer Korrelationskoeffizient | 1

Spearman’scher Rangkorrelationskoeffizient \rho

  • Annahme: Monotone Beziehung
  • Rohwerte x_i, y_i werden in Ränge X_i, Y_i umgewandelt.
  • Differenzen zwischen den Rängen der einzelnen Beobachtungen der beiden Variablen werden berechnet: D_i = X_i - Y_i
  • r_s ist dann gegeben durch:

r_s = 1-\frac{6\sum D_i^2}{n(n^2-1)}~~~\text{mit n = Anzahl der Rangpaare}

  • Analog zum Pearson Korrelationskoeffizienten liegt r_s zwischen -1 und 1 und das Vorzeichen zeigt eine positive oder negative Korrelation an.

Nichtparametrischer Korrelationskoeffizient | 2

Kendall’sches Tau \tau

  • Annahme: Monotone Beziehung
  • Im Gegensatz zum Spearman’schen \rho nutzt das Kendall’sche \tau nur den Unterschied in den Rängen und nicht die Differenz der Ränge.
  • In der Regel ist der Wert des Kendall’schen \tau etwas kleiner als der Wert des Spearman’schen \rho.
  • \tau erweist sich darüber hinaus auch
    • für intervallskalierte Daten als hilfreich,
    • die Skalen ungleiche Teilungen aufweisen oder
    • bei sehr kleinen Stichprobengrößen.

Korrelationstests in R

Pearson Korrelation in R | Vektoren

Syntax
cor(x, y, method = "pearson")
# oder alternativ (weil 'pearson' Standard ist):
cor(x, y)
  • x und y sind in diesem Falle einzelne Vektoren.
Beispiel iris
cor(x = iris$Sepal.Length, y = iris$Sepal.Width)
[1] -0.118

Pearson Korrelation in R | Data frames

  • Es können aber auch ganze data frames oder Matrizen an x bzw. x und y übergeben werden (alle Spalten müssen numerisch sein!).
    • → dann wird der Korrelationskoeffizient für alle paarweisen Vergleiche der Spalten ausgegeben:
Beispiel iris
cor(x = iris[ ,1:4]) # wichtig: ohne 'Species'
             Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length        1.000      -0.118        0.872       0.818
Sepal.Width        -0.118       1.000       -0.428      -0.366
Petal.Length        0.872      -0.428        1.000       0.963
Petal.Width         0.818      -0.366        0.963       1.000

Pearson Korrelationstest in R

Um zu testen, ob die Beziehung signifikant ist, kann die Funktion cor() erweitert werden zu cor.test():

Syntax
cor.test(x, y, method = "pearson") 
# oder einfach nur 
cor.test(x, y)


  • H0: \rho ist gleich Null
  • Durchführung eines t-Test mit der Kenngröße t = \frac{r}{s_r} und den Freiheitsgraden n-2
Beispiel iris
cor.test(x = iris$Sepal.Length, 
  y = iris$Sepal.Width)

    Pearson's product-moment correlation

data:  iris$Sepal.Length and iris$Sepal.Width
t = -1, df = 148, p-value = 0.2
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.2727  0.0435
sample estimates:
   cor 
-0.118

Spearman/Kendall Korrelation in R

Beispiel iris
sl <- iris$Sepal.Length
sw <- iris$Sepal.Width

cor(x = sl, y = sw, method = "pearson")
[1] -0.118
cor(x = sl, y = sw, method = "spearman")
[1] -0.167
cor(x = sl, y = sw, method = "kendall")
[1] -0.077

Spearman/Kendall Korrelationstest in R

cor.test(x = sl, y = sw, method = "spearman")

    Spearman's rank correlation rho

data:  sl and sw
S = 656283, p-value = 0.04
alternative hypothesis: true rho is not equal to 0
sample estimates:
   rho 
-0.167 
cor.test(x = sl, y = sw, method = "kendall")

    Kendall's rank correlation tau

data:  sl and sw
z = -1, p-value = 0.2
alternative hypothesis: true tau is not equal to 0
sample estimates:
   tau 
-0.077

Handling von fehlenden Werten bei cor()

  • Bei Argument use → ‘pairwise.complete.obs’ auswählen, um die paarweisen Werte mit NA zu entfernen.
Ohne Einstellung des Arguments 'use'
cor(x = c(31,74,58,25), y = c(19,28,NA,26), method = "pearson")
[1] NA
Mit Einstellung des Arguments 'use'
cor(x = c(31,74,58,25), y = c(19,28,NA,26), method = "pearson", 
  use = "pairwise.complete.obs")
[1] 0.585

Viele Beziehungen visualisieren | 1

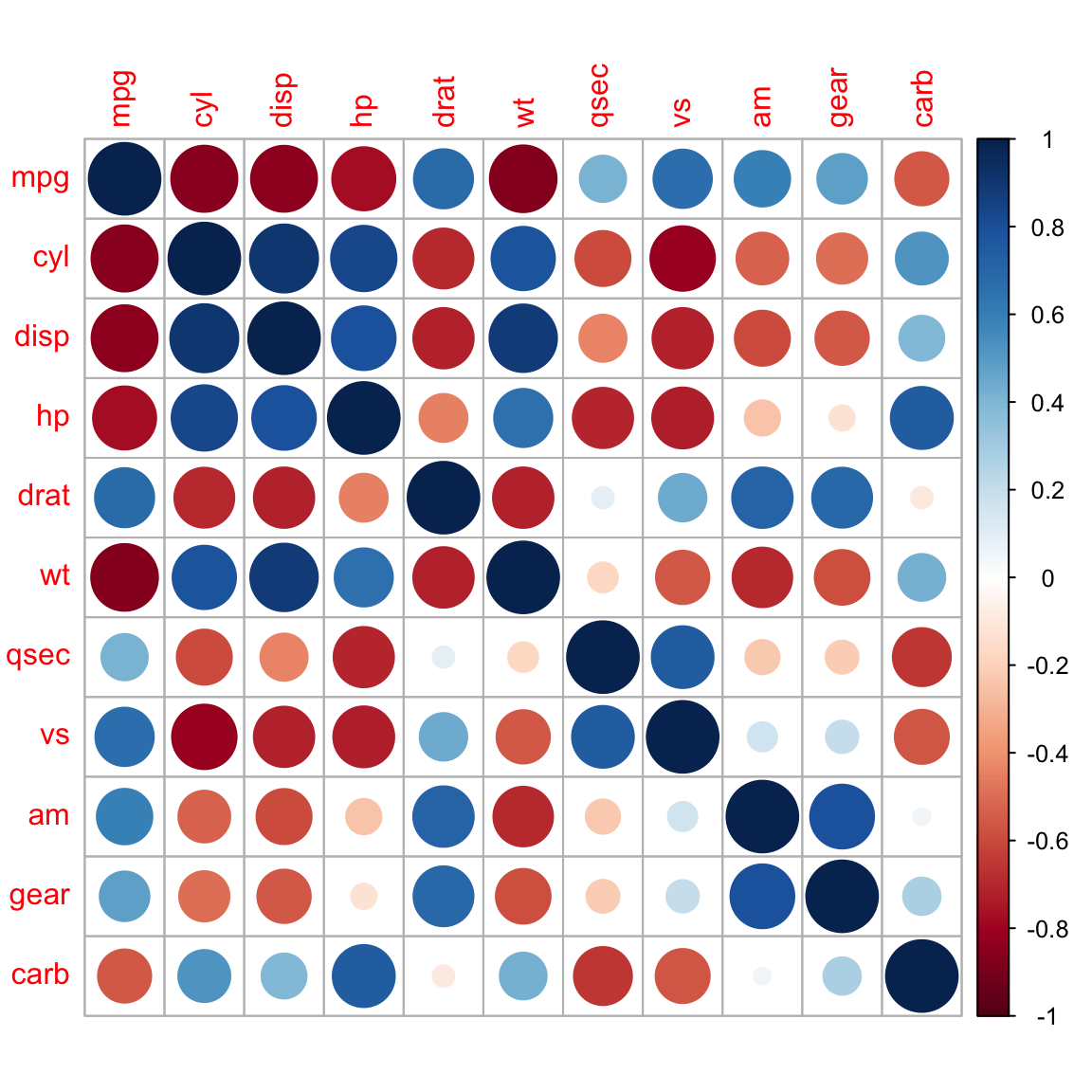
Das corrplot Paket

  • Vignette: https://cran.r-project.org/web/packages/corrplot/vignettes/corrplot-intro.html
  • Grafische Darstellung einer gesamten Korrelationsmatrix.
  • Enthält einige Algorithmen zur Anordnung der Matrix.
  • Viele Einstellungen möglich (Farben, Textbeschriftung, Farbetiketten, Layout usw.).
  • 7 Visualisierungsmethoden: ‘circle’, ‘square’, ‘ellipse’, ‘number’, ‘shade’, “’color”, ’pie’*.
  • Positive Korrelationen werden in blauer und negative Korrelationen in roter Farbe dargestellt.
  • Farbintensität und Größe der Form sind proportional zu den Korrelationskoeffizienten.

Viele Beziehungen visualisieren | 2

Das corrplot Paket

Beispiel 'mtcars'
data(mtcars)
# Korr.matrix erstellen
M <- cor(mtcars)

# vorher installieren!!
library(corrplot) 
corrplot(M)

Transformation

Wann transformieren?


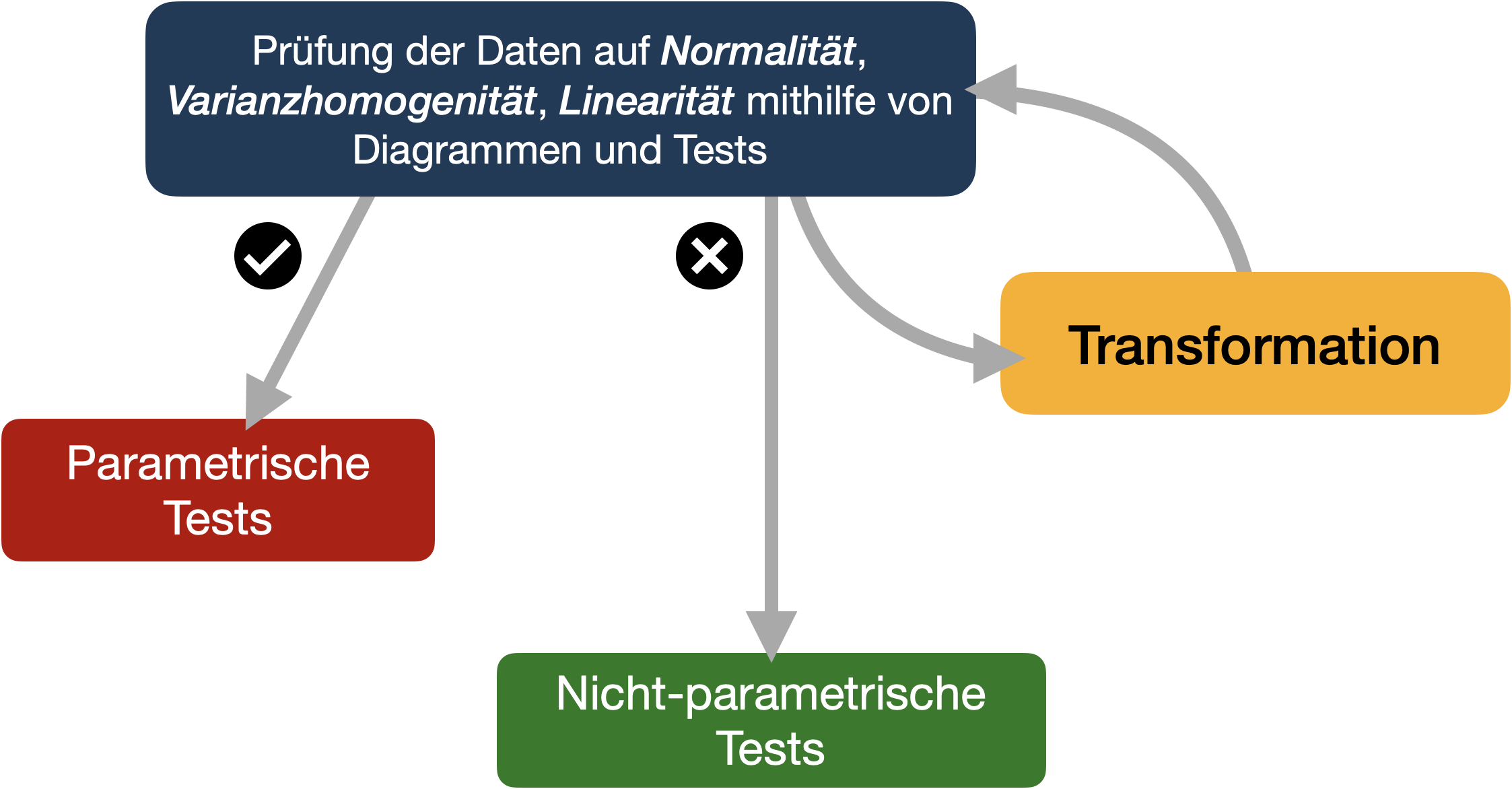
Wozu transformieren?

  • Verteilung der Daten normalisieren.
  • Streuung reduzieren und Varianzen zwischen Gruppen angleichen.
  • Einfluss von Ausreißern reduzieren.
  • Beziehung zwischen Variablen linearer machen (für Korrelationen und Regressionsanalysen)

Die richtige Wahl

  • Die Wahl der “richtigen” Transformation kann schwierig sein und basiert, zumindest teilweise, auf Erfahrung.
  • Einflussfaktoren:
    • Fragestellung
      • Sind extremere Werte von Interesse oder die am häufigsten vorkommenden?
      • Bei Gemeinschaftsanalysen: geht es darum, welche Arten vorkommen oder mehr um die relativen Abundanzen der Arten (dominante vs. seltene Arten)?
    • Wahl der Analysemethode
      • Welche Annahmen müssen erfüllt sein?
      • Muss das Skalenniveau (z.B. das metrische) erhalten bleiben? (Korrelationen können beispielsweise nicht mit nominalen Daten gemacht werden)

Aus DS1: Umwandlung des Skalenniveaus

Das Skalenniveau lässt sich umwandeln, allerdings kann dies immer mit einem Informationsverlust einhergehen.

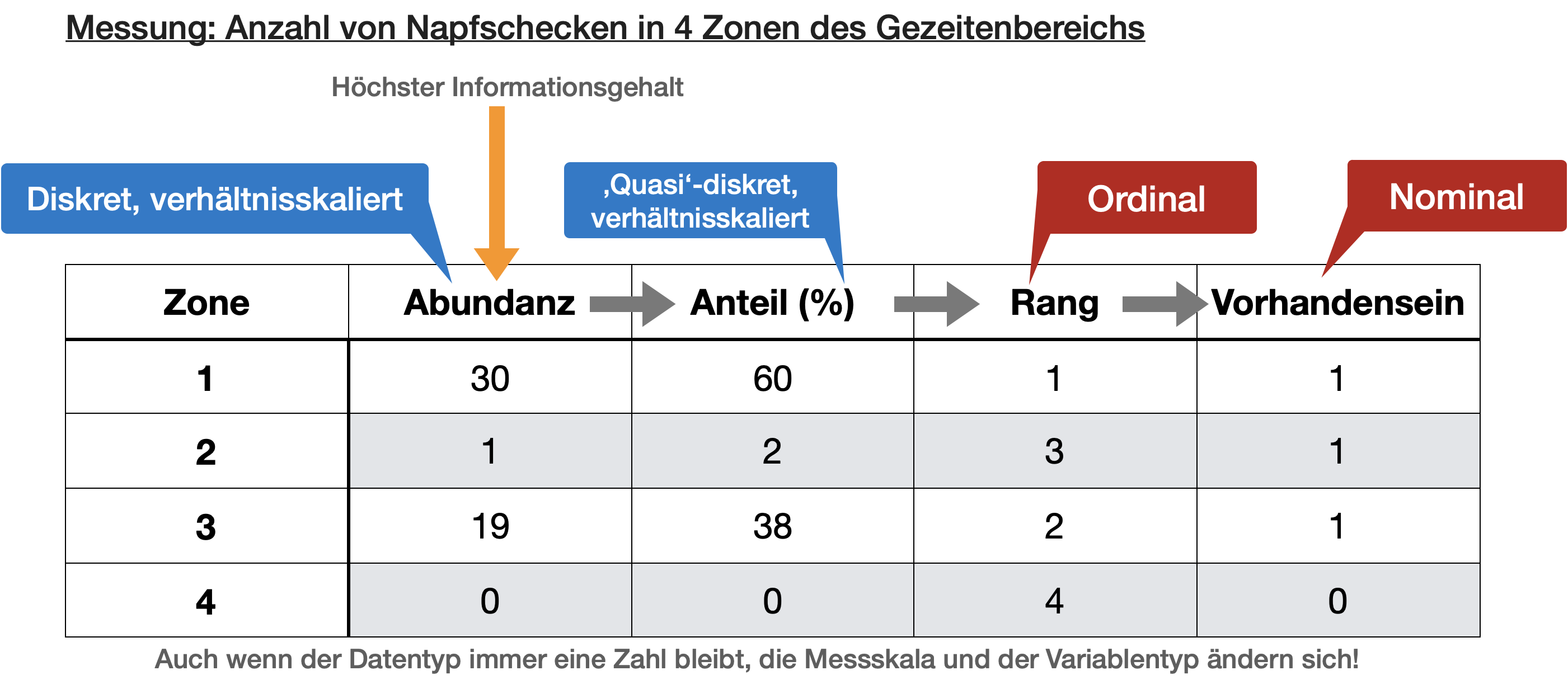
Häufig angewandte Transformationen

Wurzeltransformation sqrt()

  • Geeignet für Häufigkeitsdaten (‘count data’).
  • Quadratwurzel → wenn Varianz = Mittelwert oder Daten Poisson-verteilt sind.
  • Vierte Wurzel → wenn die Varianz > Mittelwert entspricht oder Daten negativ binomial-verteilt sind.
x <- c(0, 1, 10, 100, 5)
sqrt(x) # oder: x^0.5
[1]  0.00  1.00  3.16 10.00  2.24
sqrt(sqrt(x)) # oder: x^0.25
[1] 0.00 1.00 1.78 3.16 1.50

Logarithmus log()

  • Geeignet wenn Varianzen >> Mittelwert.
  • Wenn der Datensatz Nullen enthält wird zu jeder Beobachtung eine Konstante addiert.
x <- c(0, 1, 10, 100)
log(x + 0.1)  # natürlicher Log
[1] -2.3026  0.0953  2.3125  4.6062
log10(x + 0.1) # Log zur Basis 10
[1] -1.0000  0.0414  1.0043  2.0004

Arkussinus asin()

  • Geeignet für Prozente und Proportionen, die nicht normalverteilt sind.
x <- c(0, 0.1, 0.2, 0.5, 1)
asin(x)
[1] 0.000 0.100 0.201 0.524 1.571

Powertransformation

  • Familie von Transformationen die nur angewendet werden können, wenn die Daten nicht negativ sind → ansonsten Konstante dazu addieren.
  • Die Powertransformation wird durch einen Potenzparameter {\lambda} (lambda) definiert:
    • x^{\lambda} wenn \lambda \neq 0 und log(x) wenn \lambda = 0
  • Alternativ Box-Cox-Transformation wählen (Box & Cox, 1964):
    • \frac{x^{\lambda} - 1}{\lambda}, wenn \lambda \neq 0 und log(x), wenn \lambda = 0

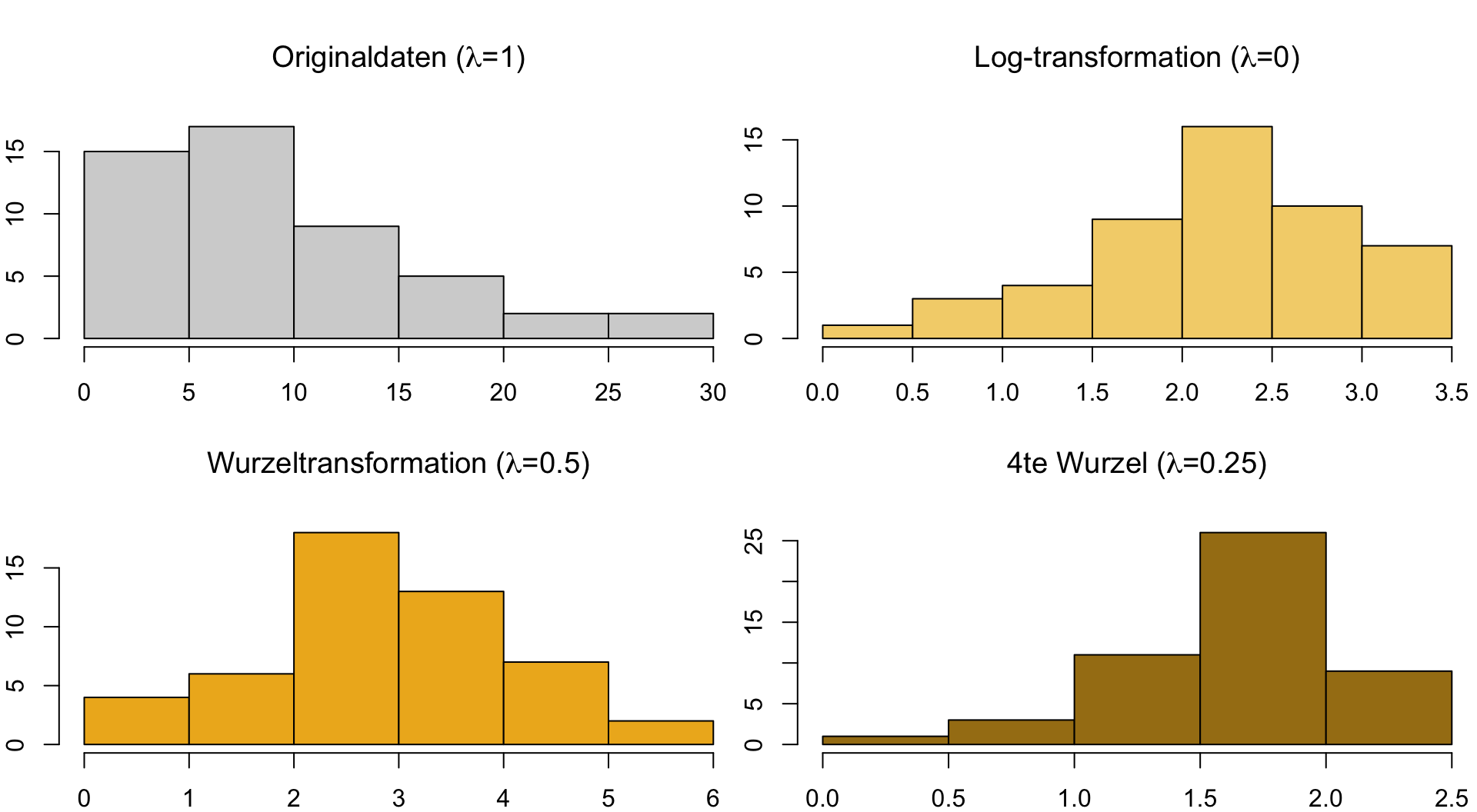
Die Powertransformation umfasst viele traditionelle Transformationen

  • {\lambda} = 0.50: Quadratwurzel-Transformation
  • {\lambda} = 0.25: 4te Wurzel-Transformation
  • {\lambda} = 0: natürlicher Logarithmus
  • {\lambda} = 1: keine Transformation

Powertransformation | Vergleich versch. \lambda

Vergleich Power- vs. Box-Cox-Transformation

\lambda = 0.5

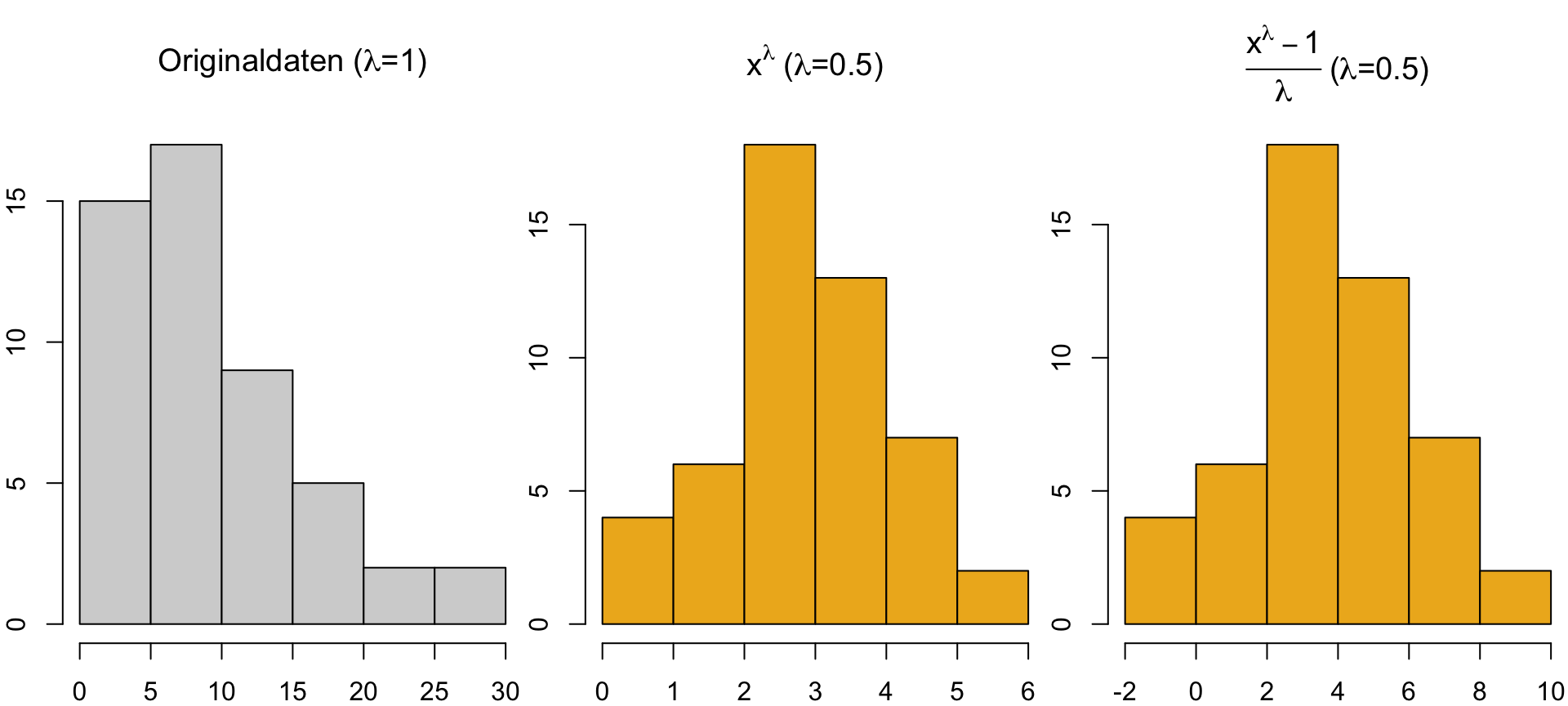
Aus DS1: Linearisierung durch Transformation

Allgemeines Schema

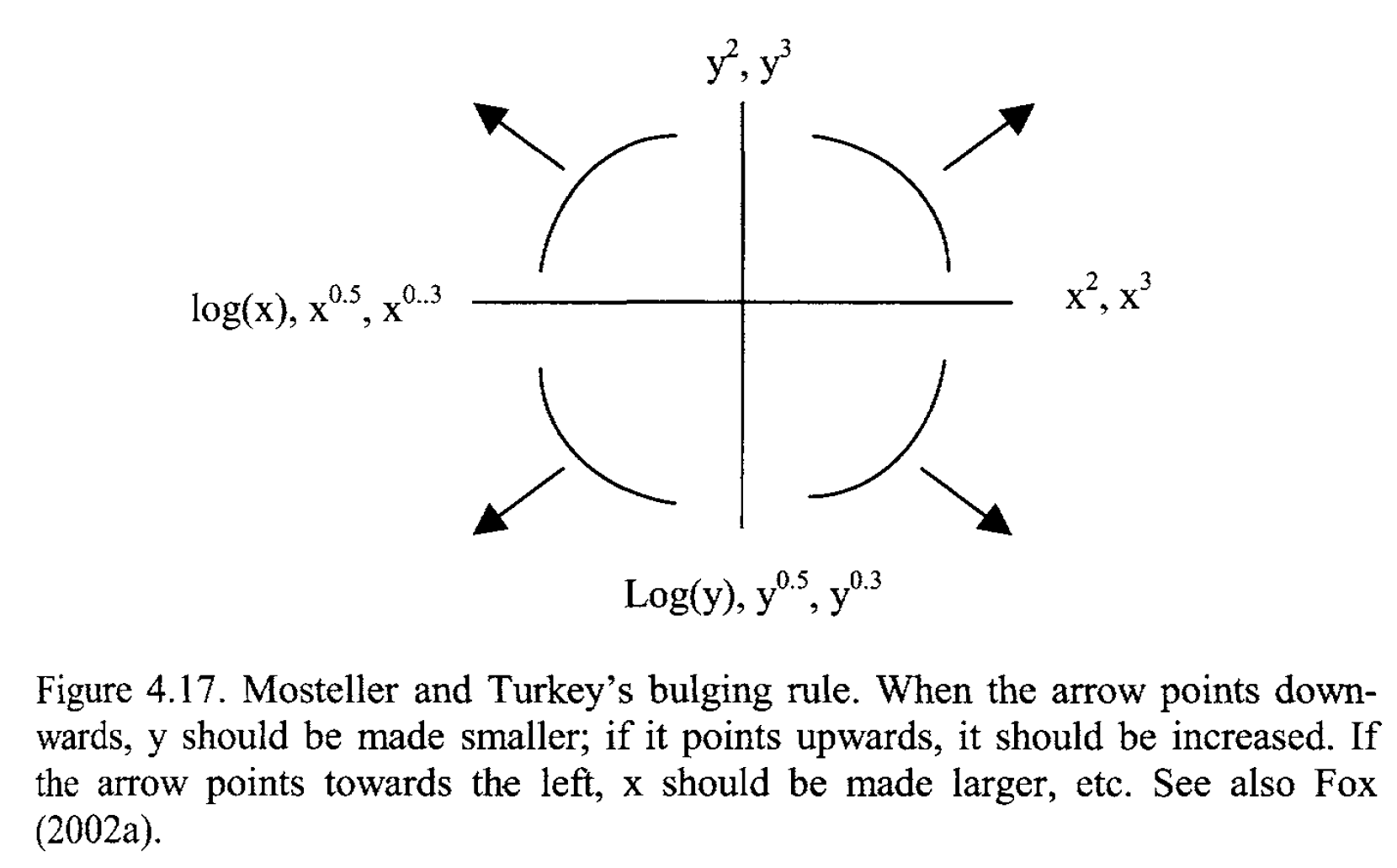
Bildquelle: Zuur et al., 2007 (Kap. 4)

Aus DS1: Anwendung der ‘bulging’ Regel

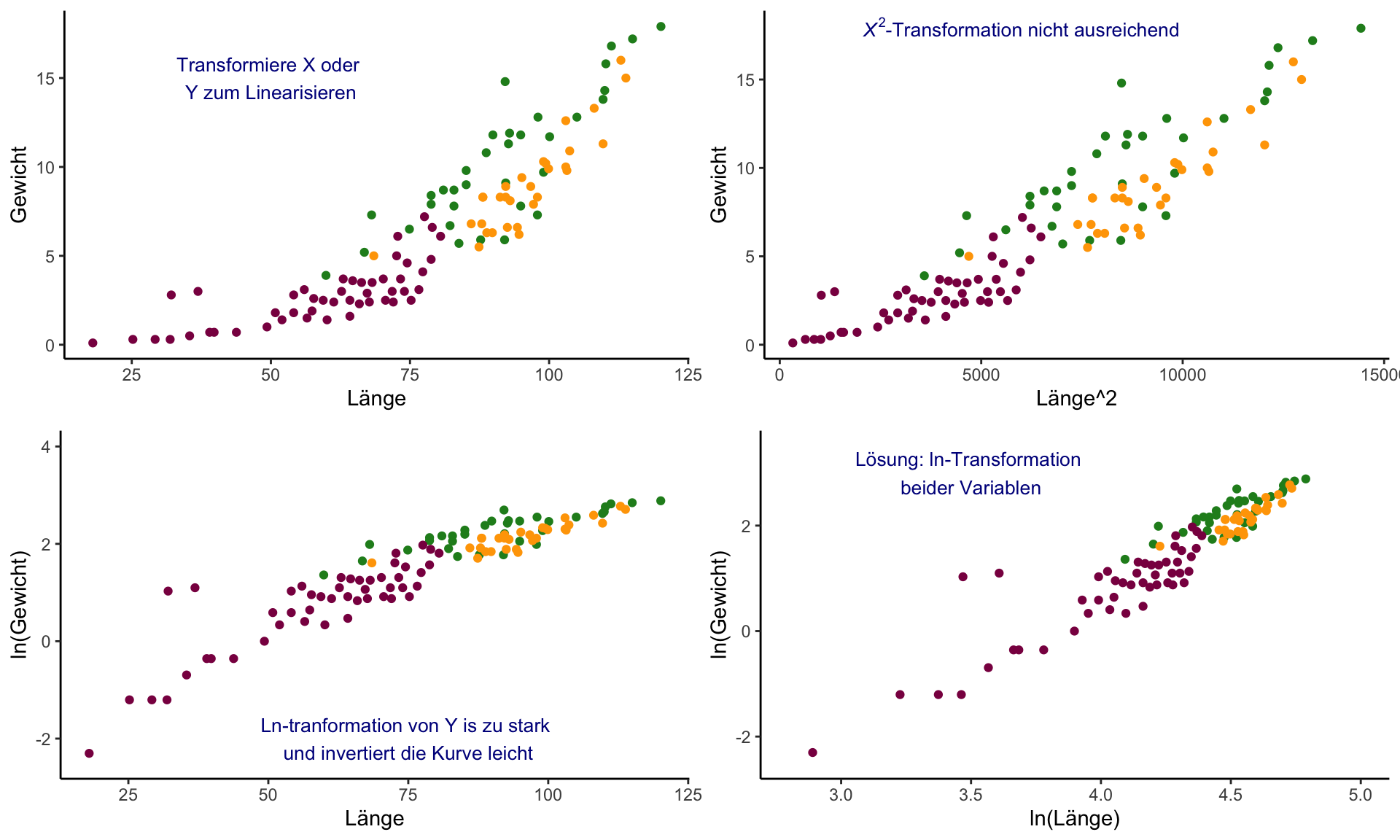
Your turn …

03:00

Quiz | Shiny App 1

Welches Lambda zur Datennormalisierung?

Link zur Shiny-App: teaching-stats/transformations/normality/

Quiz | Shiny App 2

Welches Lambda zum Angleichen von Varianzen?

Link zur Shiny-App: teaching-stats/transformations/variance-homogeneity/

Quiz | Shiny App 3

Welches Lambda zur Linearisierung?

Link zur Shiny-App: teaching-stats/transformations/linearity/

Übungsaufgaben

Vorbereitungsaufgabe für Übungstag 5

s. Handbuch - Abschnitt ‘Übungen’, Aufgabe 5.1

Was ist zu tun?

Eigene Simulationen zu Powertransformationen mithilfe von Shiny Apps durchführen:

Wichtig

Moodle-Quiz VOR der nächsten Übung ausfüllen!

Fragen?

Abschlussquiz

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de

Creative Commons License
Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.

Kurswebseite: Data Science 2