8-Mehrstichprobentests & ANOVA

Data Science 2

Saskia Otto & Monika Eberhard

Universität Hamburg, IMF & IZS

Sommersemester 2025

Lernziele

Nach Abschluss dieser VL und Übung..

können Sie auf Unterschiede bei mehr als 2 Gruppen testen.
kennen Sie das Problem des multiplen Vergleichs und können die sog. family-wise error rate (FWER) berechnen.
kennen Sie den Kruskal-Wallis-Test und die Varianzanalyse und wissen, wann diese jeweils eingesetzt werden können.
können Sie systematische und unsystematische Einflüsse in den Daten mittels Varianzanalyse mathematisch trennen und bestimmen.
wissen Sie, wie die Sie das Ergebnis einer Varianzanalyse (den ‘F-Wert’) interpretieren und bewerten sollen?
wissen Sie, welche Arten des Post-hoc-Vergleichs es gibt und wie Sie diese anwenden.

Heutige Frage

Hat der Käfigtyp einen Einfluss auf das mittlere Gewicht des Atlantischen Lachses (Salmo salar) bzw. gibt es Unterschiede im durchschnittlichen Lachsgewicht zwischen den vier getesteten Käfigtypen?

Mittelwerte von ≥ 3 Stichproben vergleichen

Das Problem der multiplen Vergleiche

Beispiel:

Auswirkung der Meerestiefe auf das bakterielle Wachstum
Probenahme in 5m (Kontrolle), 10m, 20m, 40m, 80m, 160m
H_A: das bakt. Wachstum unterscheidet sich zwischen den 6 Tiefenstufen.
→ Warum nicht jede Tiefe mit der Kontrolle mittels t-Test vergleichen?

Sehr ineffizient!!! 5 Tests sind notwendig

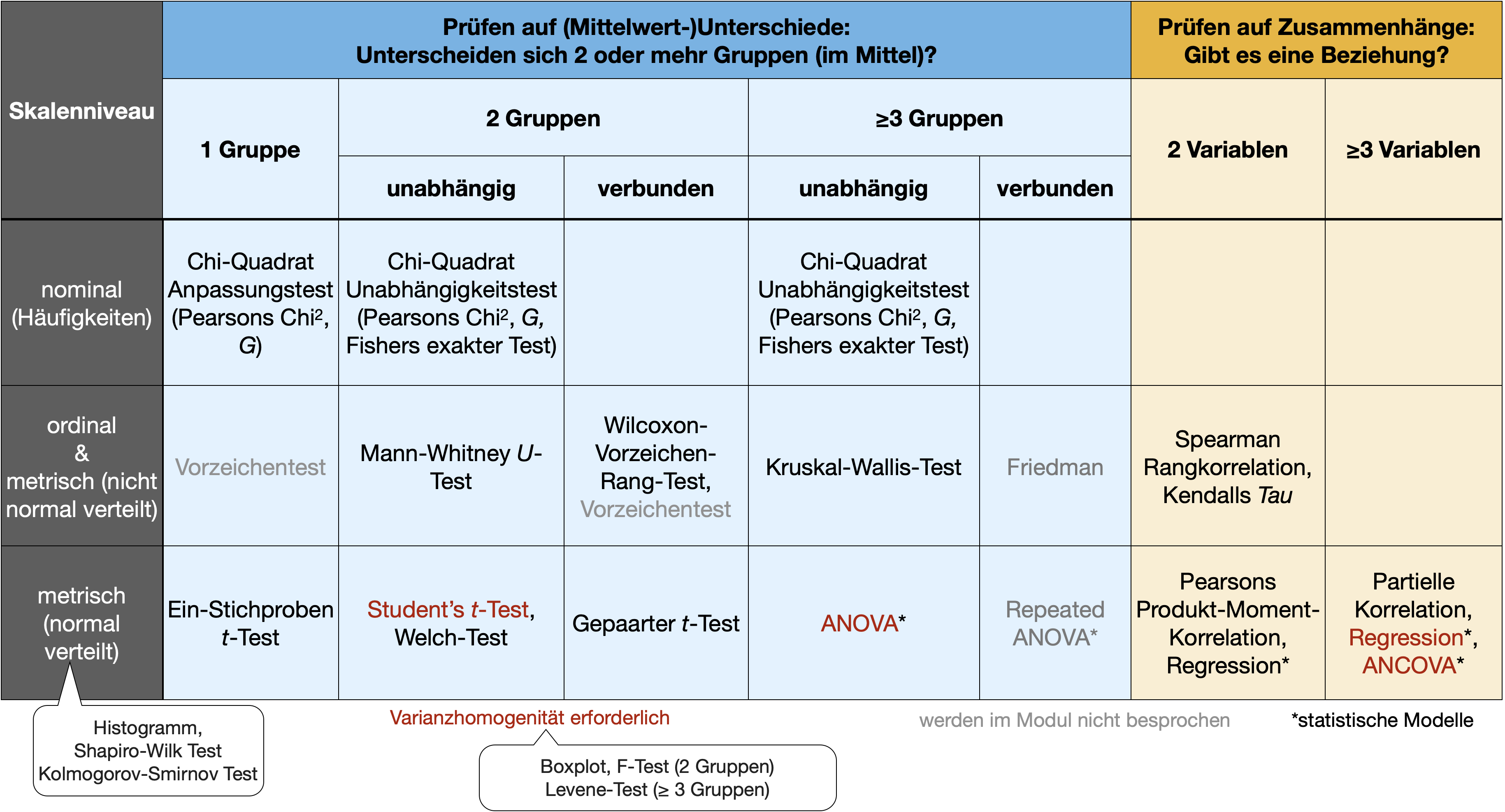
‘Familywise Error Rate’ (FWER)

Je öfter ein Test mehrfach auf eine Hypothese angewendet wird, desto höher ist das Risiko eines stat. Fehlers 1. Art (Ablehnen einer korrekten H0).
Die FWER ist dabei definiert durch die Wahrscheinlichkeit, mindestens eine der Testhypothesen fälschlicherweise abzulehnen:
- \alpha_{FWER} = 1-(1-\alpha)^c \Rightarrow 1-(1-0.05)^5 = 0.23 (c = Anzahl der Vergleiche)
- => Die Wahrscheinlichkeit, dass mindestens ein Vergleich zu einem stat. Fehlers 1. Art führt, beträgt 23%.

Lösungen zur Kontrolle der FWER

1. Mehrstichprobentest

Nicht-parametrisch:
- Kruskal-Wallis-Test (H-Test)
- Friedman-Test (Friedman-Rangsummentest)
Parametrisch:
- Varianzanalyse (ANOVA)

2. Paarweise Tests

Bonferroni-Korrektur
Spezifische Tests für multiple Mittelwertvergleiche (sog. Post-hoc-Tests):
- Tukey’s, SNK, Ryan’s etc.
- Passen Signifikanzniveaus auf unterschiedliche Weise an.

Nicht-parametrische Mehrstichprobentests

Unabhängige Stichproben

Kruskal-Wallis-Test (H Test)

Logische Erweiterung des Mann Whitney U-Tests, Messung kann also auch auf einer Ordinalskala erfolgen
Rang-basiertes Gegenstück zur 1-faktoriellen ANOVA → allerdings nur 95% der Teststärke
Stichprobengröße der Gruppen kann unterschiedlich sein
Annahme: Stichproben sollten annähernd die gleiche Verteilung haben

H=\frac{12}{N*(N+1)}*\left( \sum\frac{R_i^2}{n_i} \right)-3*(N+1)

N = Gesamter Stichprobenumfang, n_i = Anzahl Messung pro Gruppe i, R_i = Summe der Ränge pro Gruppe i

Kruskal-Wallis-Test | Einzelschritte

Die Rohdaten aus den k Stichproben/Gruppen werden zu N Elementen zusammengefasst und dann vom niedrigsten zum höchsten Rang geordnet.
Gleiche Werte werden mit dem Mittelwert der jeweiligen Ränge versehen.
Diese Ränge werden dann wieder in die k Gruppen einsortiert.
Bildung der Rangsummen pro Gruppe i=1 bis k
Berechnung der Teststatistik H.
- Wenn mehr als 25 % den gleichen Rang haben, muss die H-Statistik korrigiert werden.
Prüfverteilung
- Wenn n_i < 6 und k = 3 wird die H-Test-Tabelle verwendet.
- Wenn n_i ≥ 6 und k > 3 ist H näherungsweise \chi^2-verteilt (df = k-1).
Die H_0 ist immer 2-seitig! Es wird aber rechtsseitig getestet → wenn H > H_{krit}, gibt es sign. Unterschiede zwischen mind. 2 Gruppen.

Kruskal-Wallis-Test in R | Beispiel iris

Rangsummenbildung

df <- iris |>
  mutate(ranks_sl = rank(Sepal.Length, ties.method = "average")) |>
  group_by(Species) |>
  summarise(sum_ranks = sum(ranks_sl))
df

# A tibble: 3 × 2
  Species    sum_ranks
  <fct>          <dbl>
1 setosa         1482 
2 versicolor     4132.
3 virginica      5710.

Teststatistik H und p-Wert

(h_sl <- 12/(150*(150+1))*sum(df$sum_ranks^2/50) - 3*(150+1))

[1] 96.8

pchisq(h_sl, df = 3-1, lower.tail = FALSE)

[1] 9.74e-22

Kruskal-Wallis-Test in R | `kruskal.test()`

Vektorsyntax

# x = abhängige Variable, g = Gruppierungsvariable/Faktor
kruskal.test(x = iris$Sepal.Length, g = iris$Species)


    Kruskal-Wallis rank sum test

data:  iris$Sepal.Length and iris$Species
Kruskal-Wallis chi-squared = 97, df = 2, p-value <2e-16

Formelsyntax

# kruskal.test(x ~ g, data)
kruskal.test(Sepal.Length ~ Species, data = iris)


    Kruskal-Wallis rank sum test

data:  Sepal.Length by Species
Kruskal-Wallis chi-squared = 97, df = 2, p-value <2e-16

Abhängige Stichproben

Friedman-Test

Rang-basiertes Gegenstück zur 1-faktoriellen ANOVA mit wiederholten Messungen
Messung kann auch auf einer Ordinalskala erfolgen
Anwendbar auf vollständige Blockdesigns
Teststärke oder Effizienz: abhängig vom k/n-Verhältnis

F_r=\left( \frac{12}{n*k*(k+1)}*\left( \sum R_i^2\right)\right)-3*n*(k+1)

n = Anzahl der Blöcke, k = Anzahl der Gruppen, R_i = Summe der Ränge pro Gruppe i

Built-in Funktion: friedman.test()

friedman.test(y, groups, blocks)
friedman.test(y ~ groups|blocks, data) # Formelsyntax

# y = abhängige Variable, groups = Messwiederholung, 
# blocks = zu untersuchende Objekte

Your turn …

01:30

Quiz | Kronblattweite in iris

Es soll die Hypothese getestet werden, dass sich die durchschnittliche Kronblattweite der drei Iris Arten unterscheidet.

kruskal.test(Petal.Width ~ Species, data = iris)


    Kruskal-Wallis rank sum test

data:  Petal.Width by Species
Kruskal-Wallis chi-squared = 131, df = 2, p-value <2e-16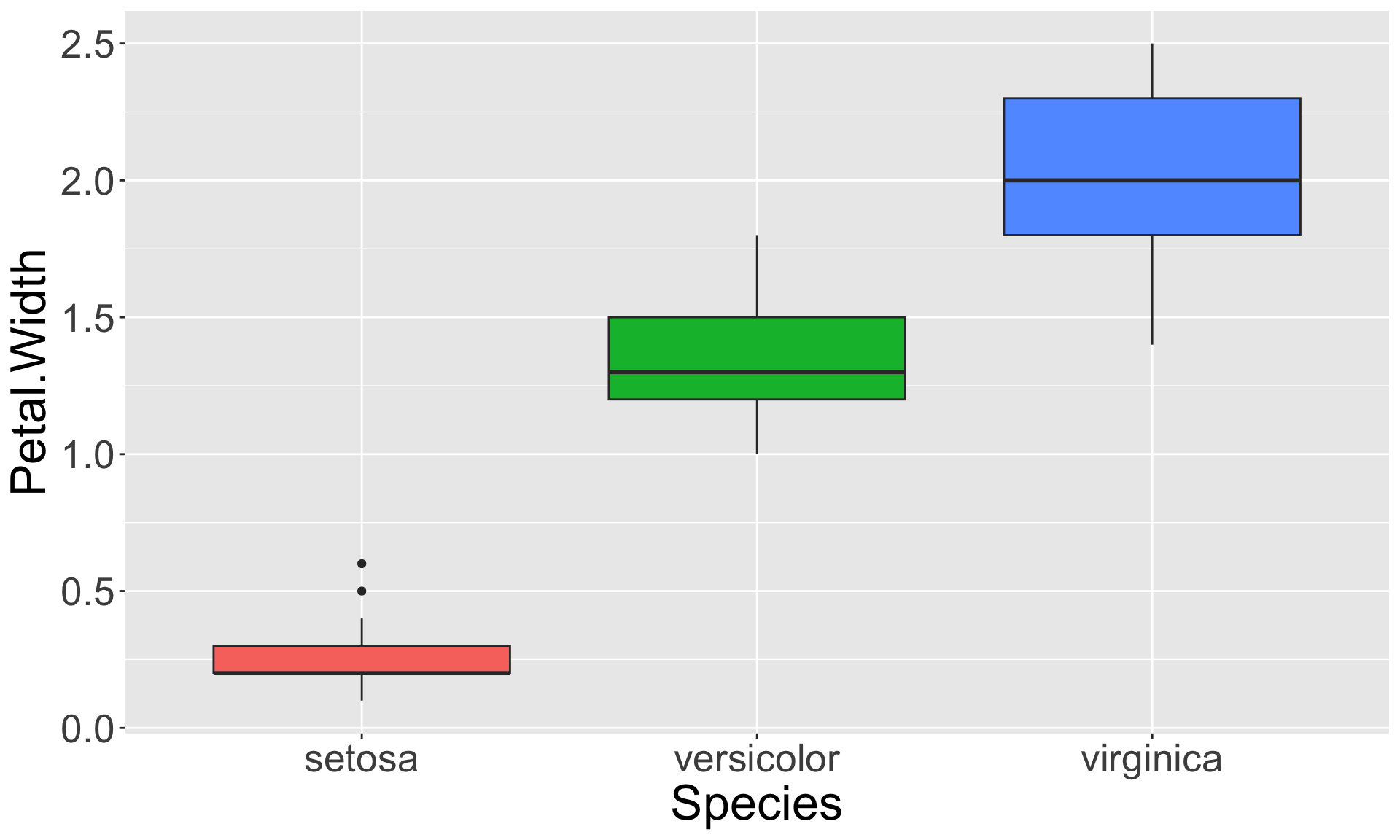

Varianzanalyse (ANalysis Of VAriance)

Was ist die Varianzanalyse oder ANOVA?

In seiner einfachsten Form die Erweiterung der t-Statistik für mehrere Stichproben.
Eine weit verbreitete statistische Methode.
Testet auf Mittelwertunterschiede, indem die geschätzte Gesamtvariabilität in den Daten in 2 Teile zerlegt wird:
- Variabilität innerhalb (‘within’) der verschiedenen Gruppen.
- Variabilität zwischen (‘between’) den verschiedenen Gruppen.
Wenn sich die Varianzen zwischen den Stichproben unterscheiden, müssen sich auch die Mittelwerte zwischen den Stichproben unterscheiden!

Variablen-Typen

y = abhängige oder Antwortvariable
- Datentyp ist metrisch (diskret oder stetig)
x = 1 oder mehrere unabhängige Variable(n)
- Datentyp ist kategorial, auch Faktor genannt
- Einzelne Kategorien werden Faktorstufen oder Gruppen genannt.
- → in R explizit als factor definieren!
→ Auch hier müssen die Daten im langen Format vorliegen!

ANOVA-Typen

1 Faktor = einfaktorielle Varianzanalyse (1-way ANOVA)
2 Faktoren = zweifaktorielle Varianzanalyse (2-way ANOVA)
≥3 Faktoren = mehrfaktorielle Varianzanalyse (multi-way ANOVA)
Wenn >1 Faktor
- geschachteltes (nested) vs. gekreuztes (crossed) Design
- fixed vs. random vs. mixed effect model
- mit/ohne Messwiederholung, Blockdesign

Das Prinzip der ANOVA | 1

Variabilität innerhalb Gruppen << zwischen Gruppen

Das Prinzip der ANOVA | 2

Variabilität innerhalb Gruppen << zwischen Gruppen

Das Prinzip der ANOVA | 3

Variabilität innerhalb Gruppen >> zwischen Gruppen

Das Prinzip der ANOVA | 4

Variabilität innerhalb Gruppen >> zwischen Gruppen

Varianzzerlegung

Ein Anwendungsbeispiel

Lachszucht

Frage: Hat der Käfigtyp einen Einfluss auf das mittlere Gewicht des Atlantischen Lachses (Salmo salar)?
Antwortvariable y: Körpergewicht [in kg]
Faktor x: Käfigtyp
- 4 Gruppen: A,B,C,D
Replikate sind Individuen pro Käfig i (n_i = 24)

Erklärte vs. nicht erklärte Varianz | 1

Gesamtmittelwert: 2.5 | Gesamtvarianz 0.33

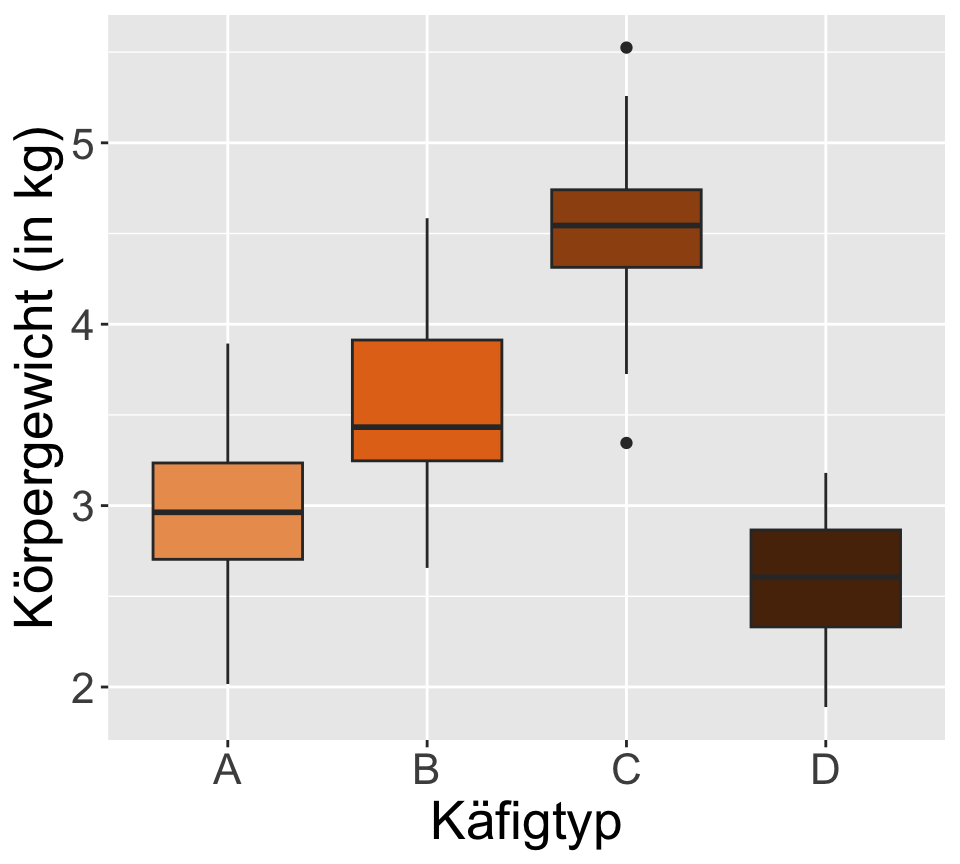
Replikat	Typ A	Typ B	Typ C	Typ D
1	2.0	2.7	2.9	2.2
2	2.7	2.0	1.9	2.0
3	2.2	3.8	2.7	3.1
4	3.1	1.5	2.5	2.7
…	…	…	…	…
Gruppenmittelwert	2.5	2.5	2.5	2.5
Gruppenvarianz	0.25	0.99	0.19	0.25

Behandlungen (hier = Käfigtypen) erklären NICHTS
- SS_{Groups} (between) = 0
- SS_{Residual} (within) = SS_{Total}

Erklärte vs. nicht erklärte Varianz | 2

Gesamtmittelwert: 2.5 | Gesamtvarianz 2.64

Replikat	Typ A	Typ B	Typ C	Typ D
1	5.0	4.1	2.9	0.8
2	5.0	4.1	2.9	0.8
3	5.0	4.1	2.9	0.8
4	5.0	4.1	2.9	0.8
…	…	…	…	…
Gruppenmittelwert	5.0	4.1	2.9	0.8
Gruppenvarianz	0	0	0	0

Behandlungen (hier = Käfigtypen) erklären ALLES
- SS_{Groups} (between) = SS_{Total}
- SS_{Residual} (within) = 0

Typische ANOVA Tabelle

Sources of variation	SS	df	MS	F
Groups (between)	n_i\sum_{i=1}^{p}(\bar{y_i}-\bar{y})^2	p-1	\frac{SS_{Groups}}{(p-1)}	\frac{MS_{Groups}}{MS_{Residuals}}
Residuals (within)	\sum_{i=1}^{p}\sum_{j=1}^{n}(y_{ij}-\bar{y_i})^2	p(n-1)	\frac{SS_{Residuals}}{p(n-1)}
Total	\sum_{i=1}^{p}\sum_{j=1}^{n}(y_{ij}-\bar{y})^2	pn-1

H0:
- Kein Unterschied zwischen den Gruppenmitteln \mu_1 = \mu_2 = ... = \mu_i = \mu
Sowohl MS_{Groups} als auch MS_{Residuals} schätzen \sigma^2 → Quotient = 1
F-Ratio folgt F-Verteilung mit df_{Groups} und df_{Residuals}

ANOVA Tabelle | Beispiel Lachszucht

Sources of variation	SS	df	MS	F	p
Groups	50.66	4-1	16.888	83.77	<2e-16
Residuals (or within)	18.55	4*(24-1)	0.202
Total	69.21	4*24-1

Die mittleren Gewichte von Atlantischem Lachs, der in verschiedenen Käfigen gezüchtet wurde, unterscheiden sich mindestens bei einem Käfigtyp.
- → Der Käfigtyp hat einen signifikanten Einfluss auf das mittlere Körpergewicht.
ABER: wir wissen noch nicht, welche Gruppe sich unterscheidet und wie groß die Unterschiede sind!

ANOVA in R

Built-in Funktion `aov()`

mod <- aov(formula = y ~ x, data = NULL, 
           projections = FALSE, qr = TRUE, 
           contrasts = NULL, ...)

summary(mod)

Nachdem sich zeigte, dass alle Annahmen erfüllt sind, kann die ANOVA durchgeführt werden:

mod <- aov(formula = weight ~ cages, data = salmon)
summary(mod)

            Df Sum Sq Mean Sq F value Pr(>F)    
cages        3   50.7    16.9    83.8 <2e-16 ***
Residuals   92   18.5     0.2                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Testen auf Normalverteilung INNERHALB JEDER Stichprobe mittels Shapiro-Wilk-Test:

shapiro.test(salmon$weight[salmon$cages == "A"])


    Shapiro-Wilk normality test

data:  salmon$weight[salmon$cages == "A"]
W = 1, p-value = 0.7

shapiro.test(salmon$weight[salmon$cages == "B"])


    Shapiro-Wilk normality test

data:  salmon$weight[salmon$cages == "B"]
W = 1, p-value = 0.8

shapiro.test(salmon$weight[salmon$cages == "C"])


    Shapiro-Wilk normality test

data:  salmon$weight[salmon$cages == "C"]
W = 1, p-value = 0.8

shapiro.test(salmon$weight[salmon$cages == "D"])


    Shapiro-Wilk normality test

data:  salmon$weight[salmon$cages == "D"]
W = 1, p-value = 0.5

→ Es kann bei allen vier Tests die H0 angenommen werden: die Daten sind jeweils normal verteilt.

Testen auf Varianzhomogenität ZWISCHEN den Stichproben mittels Levene-Test:

car::leveneTest(weight ~ cages, salmon)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  3    0.53   0.66
      92

→ Die H0 kann angenommen werden: die Daten sind varianzhomogen.

str(salmon)

'data.frame':   96 obs. of  2 variables:
 $ cages : Factor w/ 4 levels "A","B","C","D": 1 1 1 1 1 1 1 1 1 1 ...
 $ weight: num  2.72 2.88 3.78 3.04 3.06 ...

salmon

   cages weight
1      A   2.72
2      A   2.88
3      A   3.78
4      A   3.04
5      A   3.06
6      A   3.86
7      A   3.23
8      A   2.37
9      A   2.66
10     A   2.78
11     A   3.61
12     A   3.18
13     A   3.20
14     A   3.06
15     A   2.72
16     A   3.89
17     A   3.25
18     A   2.02
19     A   3.35
20     A   2.76
21     A   2.47
22     A   2.89
23     A   2.49
24     A   2.64
25     B   3.19
26     B   2.66
27     B   3.92
28     B   3.58
29     B   2.93
30     B   4.13
31     B   3.71
32     B   3.35
33     B   3.95
34     B   3.94
35     B   3.91
36     B   3.84
37     B   3.78
38     B   3.47
39     B   3.35
40     B   3.31
41     B   3.15
42     B   3.40
43     B   2.87
44     B   4.58
45     B   4.10
46     B   2.94
47     B   3.30
48     B   3.27
49     C   4.89
50     C   4.46
51     C   4.63
52     C   4.49
53     C   4.48
54     C   5.18
55     C   4.39
56     C   5.26
57     C   3.73
58     C   4.79
59     C   4.56
60     C   4.61
61     C   4.69
62     C   4.25
63     C   4.33
64     C   3.99
65     C   3.96
66     C   4.65
67     C   4.72
68     C   4.53
69     C   4.96
70     C   5.53
71     C   4.25
72     C   3.35
73     D   3.00
74     D   2.15
75     D   2.16
76     D   3.01
77     D   2.36
78     D   1.89
79     D   2.59
80     D   2.43
81     D   2.50
82     D   2.69
83     D   2.31
84     D   2.82
85     D   2.39
86     D   2.67
87     D   3.05
88     D   2.72
89     D   2.34
90     D   3.07
91     D   3.00
92     D   2.77
93     D   2.62
94     D   2.19
95     D   3.18
96     D   2.20

ANOVA in R | Beispiel Lachszucht 2

Überprüfung der Modellannahme posteriori

par(mfrow = c(2,2))
plot(mod)

Diese Diagnostikplots sind bei der 1-faktoriellen ANOVA allerdings nicht so wichtig.

Effektgröße Eta Quadrat (\eta^2) | 1

Die berechnete Wahrscheinlichkeit gibt nur Auskunft darüber, ob ein Ergebnis durch Zufall zustande gekommen ist oder nicht.
Die Effektstärke oder Effektgröße gibt an, wie effektiv eine Behandlung oder Intervention ist.

\eta^2 bei einer 1-faktoriellen ANOVA

\eta^2 = \frac{SS_{Groups}}{SS_{Total}}

Interpretation von \eta^2

<0.06: kleiner Effekt
0.06–0.14: mittelgradiger Effekt
>0.14: großer Effekt

Effektgröße Eta Quadrat (\eta^2) | 2

Beispiel Lachszucht

50.66 / (50.66 + 18.55)

[1] 0.732

Generischer Code

mod_sum <- summary(mod) # Abspeichern des summary Outputs
# str(mod_sum)
eta_sq <- mod_sum[[1]]$`Sum Sq`[1] / (mod_sum[[1]]$`Sum Sq`[1] +
    mod_sum[[1]]$`Sum Sq`[2] )
eta_sq

[1] 0.732

Gruppeneffekte grafisch darstellen

Mit der Funktion `plot.design()`

plot.design(weight ~ cages, data = salmon)

Gruppeneffekte in einer Gleichung ausdrücken

Alternative Formulierung der H0

Gruppeneffekte sind definiert als \alpha_i = \mu_i - \mu
Die H0 kann auch ausgedrückt werden als:
- Es gibt keinen Effekt bestimmter Behandlungsstufen (treatment effects), die Unterschiede sind nur zufällig: \alpha_1 = \alpha_2 = \alpha_3 = .. = 0

Paarweise Tests/Post-hoc-Tests

Paarweise Tests | Bonferroni-Korrektur

Kann immer angewendet werden, jedoch recht konservativ → Verlust an Teststärke
Leicht zu berechnen (Bsp. Bakterienwachstum in untersch. Tiefen):

\alpha_{adj} = \frac{\text{Signifikanzniveau}~\alpha}{\text{Anzahl der durchgeführten Tests}} \Rightarrow \frac{0.05}{5} = 0.01

Alternative Variante: Bonferroni-Holm-Verfahren (Sequenzielle Bonferroni-Methode mit höherer Teststärke)
Funktion p.adjust() wandelt unkorrigierte p-Werte in korrigierte mittels Bonferroni-, Bonferroni-Holm- und weiteren Korrekturen um.

Bonferroni Korrektur | t-Tests

Beispiel Lachszucht

Zuerst müssen die p-Werte der paarweisen t-Tests extrahiert werden:

# Datensatz ins weite Format bringen
sw <- salmon |> mutate(id = rep(1:24, 4)) |>
  pivot_wider(names_from = "cages", values_from = "weight")

# p-Werte der paarweisen t-Tests im Vektor speichern
p_vals <- c(
  t.test(sw$A, sw$B, equal.var = TRUE)$p.value,
  t.test(sw$A, sw$C, equal.var = TRUE)$p.value,
  t.test(sw$A, sw$D, equal.var = TRUE)$p.value,
  t.test(sw$B, sw$C, equal.var = TRUE)$p.value,
  t.test(sw$B, sw$D, equal.var = TRUE)$p.value,
  t.test(sw$C, sw$D, equal.var = TRUE)$p.value
)

Bonferroni Korrektur | Korrektur der p-Werte

Nun kann die p.adjust() Funktion angewendet werden:

p_vals

[1] 3.40e-04 1.51e-14 1.70e-03 3.11e-09 8.91e-10 1.80e-19

p.adjust(p_vals, method = "bonferroni")

[1] 2.04e-03 9.05e-14 1.02e-02 1.87e-08 5.35e-09 1.08e-18

p.adjust(p_vals, method = "holm")

[1] 6.80e-04 7.54e-14 1.70e-03 9.34e-09 3.57e-09 1.08e-18

Tukey’s HSD Test | `TukeyHSD()`

mod <- aov(formula = weight ~ cages, data = salmon)
TukeyHSD(mod)

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = weight ~ cages, data = salmon)

$cages
      diff    lwr     upr p adj
B-A  0.530  0.191  0.8691 0.001
C-A  1.532  1.193  1.8715 0.000
D-A -0.408 -0.747 -0.0687 0.012
C-B  1.002  0.663  1.3415 0.000
D-B -0.938 -1.277 -0.5987 0.000
D-C -1.940 -2.279 -1.6010 0.000

Übungsaufgaben

Übungstag 4

Chi-Quadrat-Test und Mehrstichprobentests

Aufgaben:
- 4.1 Klassische Tests zum Vergleich von Häufigkeiten (nominal)
- 4.2 Mehrstichprobentest
- 4.3 Nachbereitung Fallstudie: Frage 2.2
R Notebook-Skript:
- DS2_04_Uebungen_ChiQuadratTest_Mehrstichprobentests.Rmd

Fragen?

Abschlussquiz

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de

Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.

8-Mehrstichprobentests & ANOVA

Lernziele

Heutige Frage

Mittelwerte von ≥ 3 Stichproben vergleichen

Das Problem der multiplen Vergleiche

Beispiel:

Lösungen zur Kontrolle der FWER

1. Mehrstichprobentest

2. Paarweise Tests

Nicht-parametrische Mehrstichprobentests

Unabhängige Stichproben

Kruskal-Wallis-Test (H Test)

Kruskal-Wallis-Test | Einzelschritte

Kruskal-Wallis-Test in R | Beispiel iris

Kruskal-Wallis-Test in R | kruskal.test()

Abhängige Stichproben

Friedman-Test

Your turn …

Quiz | Kronblattweite in iris

Varianzanalyse (ANalysis Of VAriance)

Was ist die Varianzanalyse oder ANOVA?

Variablen-Typen

ANOVA-Typen

Das Prinzip der ANOVA | 1

Variabilität innerhalb Gruppen << zwischen Gruppen

Das Prinzip der ANOVA | 2

Variabilität innerhalb Gruppen << zwischen Gruppen

Das Prinzip der ANOVA | 3

Variabilität innerhalb Gruppen >> zwischen Gruppen

Das Prinzip der ANOVA | 4

Variabilität innerhalb Gruppen >> zwischen Gruppen

Varianzzerlegung

Ein Anwendungsbeispiel

Lachszucht

Erklärte vs. nicht erklärte Varianz | 1

Gesamtmittelwert: 2.5 | Gesamtvarianz 0.33

Erklärte vs. nicht erklärte Varianz | 2

Gesamtmittelwert: 2.5 | Gesamtvarianz 2.64

Typische ANOVA Tabelle

ANOVA Tabelle | Beispiel Lachszucht

ANOVA in R

Built-in Funktion aov()

ANOVA in R | Beispiel Lachszucht 1

ANOVA in R | Beispiel Lachszucht 2

Überprüfung der Modellannahme posteriori

Effektgröße Eta Quadrat (\eta^2) | 1

\eta^2 bei einer 1-faktoriellen ANOVA

Interpretation von \eta^2

Effektgröße Eta Quadrat (\eta^2) | 2

Beispiel Lachszucht

Gruppeneffekte grafisch darstellen

Mit der Funktion plot.design()

Gruppeneffekte in einer Gleichung ausdrücken

Paarweise Tests/Post-hoc-Tests

Paarweise Tests | Bonferroni-Korrektur

Bonferroni Korrektur | t-Tests

Beispiel Lachszucht

Bonferroni Korrektur | Korrektur der p-Werte

Tukey’s HSD Test | TukeyHSD()

Übungsaufgaben

Übungstag 4

Chi-Quadrat-Test und Mehrstichprobentests

Fragen?

Abschlussquiz

Kruskal-Wallis-Test in R | `kruskal.test()`

Built-in Funktion `aov()`

Mit der Funktion `plot.design()`

Tukey’s HSD Test | `TukeyHSD()`