7-Klassische Tests zum Prüfen auf Unterschiede: nominale Daten

Data Science 2

Saskia Otto

Universität Hamburg, IMF

Sommersemester 2024

Lernziele

Nach Abschluss dieser VL und Übung..

  • können Sie eine Verteilung auf ihre Anpassungsgüte mit dem Pearson Chi-Quadrat und dem G-Test testen.
  • können Sie zwei Variablen auf Unabhängigkeit mit dem Pearson Chi-Quadrat testen.
  • wissen Sie, welche Voraussetzungen für den Pearson Chi-Quadrat geprüft werden müssen und wann Sie besser die Yates Korrektur oder den Exakten Test nach Fisher anwenden.

Heutige Fragen

Sind Mitarbeiter des Gesundheitswesens, die keine COVID-19 Vorerkrankung hatten, verstärkt geimpft worden?

Hall et al., 2021, The Lancet

Tannenhäher

Eichelhäher

Unterscheiden sich zwei Tannenhäher- und Eichelhäherarten in ihrer Häufigkeit in verschiedenen Waldtypen?

Bildquellen: Wikipedia (Tannenhäher unter (CC BY-SA 2.0 Lizenz) und Eichelhäher unter CC BY-SA 4.0 Lizenz)

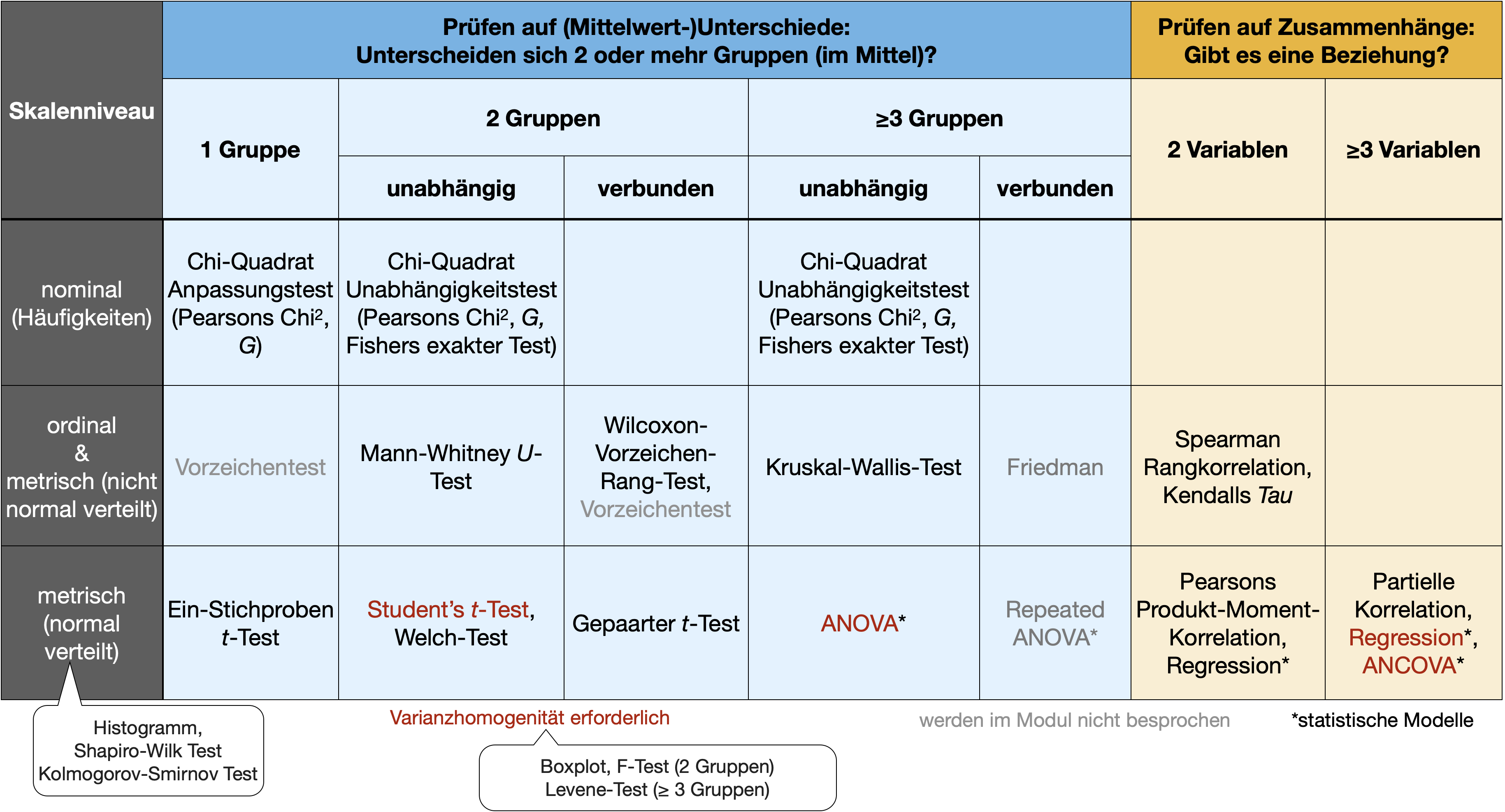
Vergleich von Häufigkeiten

Tests für nominale Daten

Häufigkeitsdaten in der Biologie

  • Viele biologische Daten liegen in Form von Zählungen (ganzen Zahlen, im Englischen count data) für ein oder mehrere Merkmale vor:
    • Anzahl vorkommender vs. abwesender Arten
    • Anzahl überlebender vs. verstorbener Tiere
    • die Anzahl der Äste an einem Baum
    • Anzahl der Beobachtungen verschiedener Phänotypen (z.B. runde grüne Erbsen, runzlige gelbe Erbsen, ..)

Bildquelle: Ravindran, 2016, PNAS

Beobachtete vs. erwartete Häufigkeiten

Frage, die sich meist stellt:

  • Weichen die beobachten Werte von den zu erwartenden Werten ab?
  • Sind zwei oder mehr Merkmale voneinander unabhängig oder weisen die beobachten Werte auf eine systematische Abhängigkeit hin?

Der Chi-Quadrat-Test | 1

  • bezeichnet eine Gruppe von Hypothesentests mit Chi-Quadrat-verteilter Testprüfgröße.
  • wird in folgende Typen unterteilt:

Grundtypen

  • Anpassungstest (im Englischen goodness-of-fit test) → prüft, ob vorliegende Daten auf eine bestimmte Weise verteilt sind.
  • Unabhängigkeitstest (contingency table test) → prüft, ob zwei oder mehr Merkmale stochastisch unabhängig sind.
  • Homogenitätstest → prüft, ob zwei oder mehr Stichproben derselben Verteilung bzw. einer homogenen Grundgesamtheit entstammen.

Der Chi-Quadrat-Test | 2

Es gibt drei Varianten die Signifikanz der Unterschiede zwischen beobachteten und erwarteten Häufigkeiten zu beurteilen:

Testvarianten

  1. Chi-Quadrat-Test nach Pearson (mit oder ohne Yates Korrektur)
  2. G-Test (auch Log-Likelihood-Test genannt)
    • kann jederzeit anstelle des Pearsons \chi^2-Test angewendet werden.
    • soll sensitiver sein, allerdings eher zum Fehler 1. Art führen.
  3. Exakter Test nach Fisher (Fisher’s exact test)

Chi-Quadrat-Tests in R

Built-in Funktion chisq.test()

chisq.test(x, y = NULL, correct = TRUE,
           p = rep(1/length(x), length(x)), 
           rescale.p = FALSE,
           simulate.p.value = FALSE, 
           B = 2000)

Anpassungtest: 1 Merkmal

Pearsons Chi-Quadrat-Test \chi ^2 vs. G-Test

Vorgehensweise

  1. Erwartete Häufigkeit muss anhand von Wahrscheinlichkeiten berechnet werden.
  2. Vergleich mit beobachteter Häufigkeit
  3. Berechnung des \chi ^2 – bzw. G-Wertes.
  4. Vergleich des \chi ^2- bzw. G-Wertes mit dem kritischen \chi ^2-Wert bei (n-1) Freiheitsgraden und einer Signifikanzschwelle von \alpha = 0.05. Es wird immer 1-seitig getestet1!

\chi^2=\sum\frac{(Beobachtungswert_i - Erwartungswert_i)^2}{Erwartungswert_i} \; \text{ und } \; G = 2\sum_{i=1}^{n}B_i\cdot ln\frac{B_i}{E_i}

Beispiel mit gleichen Wahrscheinlichkeiten | Daten

300maliges Würfeln eines 6-seitigen Würfels

Augenzahl Beobachtet Erwartet
1 59
2 33
3 48
4 51
5 65
6 44
Gesamt (N) 300

Beispiel mit gleichen Wahrscheinlichkeiten | Erwartungswerte

300maliges würfeln eines 6-seitigen Würfels

Augenzahl Beobachtet Erwartet (P(X)*N)
1 59 1/6*300 = 50
2 33 1/6*300 = 50
3 48 1/6*300 = 50
4 51 1/6*300 = 50
5 65 1/6*300 = 50
6 44 1/6*300 = 50
Gesamt (N) 300 300

H0: Es gibt keinen Unterschied zwischen den beobachteten und erwarteten Werten.

Beispiel mit gleichen Wahrscheinlichkeiten | Kennwertberechnung


\chi^2=\frac{(59-50)^2}{50}+\frac{(33-50)^2}{50}+\frac{(48-50)^2}{50}+\frac{(51-50)^2}{50}+\frac{(65-50)^2}{50}+\frac{(44-50)^2}{50} = 12.72


G = 2(59\cdot ln\frac{59}{50}+33\cdot ln\frac{33}{50}+48\cdot ln\frac{48}{50}+51\cdot ln\frac{51}{50}+65\cdot ln\frac{65}{50}+44\cdot ln\frac{44}{50}) = 13.07

Beispiel mit gleichen Wahrscheinlichkeiten | Signifikanz

Vergleich mit kritischem \chi^2-Wert

qchisq(p = 0.95, df = 6-1)
[1] 11.1
  • Unser \chi^2 ist größer als der obere kritische \chi^2-Wert → wir können unsere H0 ablehnen.
  • Die Interpretation für unseren G-Wert ist die gleiche → H0 wird abgelehnt.

Berechnung des p-Werts

pchisq(12.72, df = 6-1, lower.tail = FALSE) # chi2
[1] 0.0261
pchisq(13.07, df = 6-1, lower.tail = FALSE) # G
[1] 0.0227

Beispiel mit gleichen Wahrscheinlichkeiten | Automatische Berechnung

Anpassungstest ohne Korrektur

chisq.test(x = c(59,33,48,51,65,44), correct = FALSE)

    Chi-squared test for given probabilities

data:  c(59, 33, 48, 51, 65, 44)
X-squared = 13, df = 5, p-value = 0.03
chisq.test(x = c(59,33,48,51,65,44), correct = FALSE)$expected
[1] 50 50 50 50 50 50

Beispiel mit ungleichen Wahrscheinlichkeiten | Daten

Kreuzungsexperiment von Mendel

Bei einem Kreuzungsexperiment an Erbsen beobachtete Gregor Mendel folgende Phänotypen:

Augenzahl Beobachtet
rund-gelbe Erbsen 79
rund-grüne Erbsen 27
runzlig-gelbe Erbsen 24
runzlig-grüne Erbsen 8
Gesamt 138

Bildquelle: Wikipedia - Mariana Ruiz (CC0 Lizenz)

Beispiel mit ungleichen Wahrscheinlichkeiten | Erwartungswerte

Kreuzungsexperiment von Mendel

Aufgrund seines genetischen Modells erwartete er eine Verteilung der Nachkommen im Verhältnis 9:3:3:1:

Augenzahl Beobachtet Erwartet
rund-gelbe Erbsen 79 9/16*138 = 77.625
rund-grüne Erbsen 27 3/16*138 = 25.875
runzlig-gelbe Erbsen 24 3/16*138 = 25.875
runzlig-grüne Erbsen 8 1/16*138 = 8.625
Gesamt 138 138
  • Da es 4 Kategorien gibt, ist n = 4 und die Anzahl der Freiheitsgrade FG = n-1 = 3.

Beispiel mit ungleichen Wahrscheinlichkeiten | Signifikanz

Berechnung des Kennwerts

obs <- c(79,27,24,8)
exp <- c(77.625, 25.875, 25.875, 8.625)
# Wir nutzen die vektorisierte Berechnung in R
(chi2 <- sum((obs - exp)^2/exp) )
[1] 0.254

Vergleich mit kritischem \chi^2-Wert und Ermittlung p-Wert

qchisq(p = 0.95, df = 4-1)
[1] 7.81
pchisq(chi2, df = 4-1, lower.tail = FALSE)
[1] 0.968
  • Unser \chi^2 ist kleiner als der obere kritische \chi^2-Wert → wir können unsere H0 nicht ablehnen.

Beispiel mit ungleichen Wahrscheinlichkeiten | Built-in Funktion

Anpassungstest ohne Korrektur

mendel <- chisq.test(x = obs, p = c(9/16, 3/16, 3/16, 1/16), correct = FALSE)
mendel

    Chi-squared test for given probabilities

data:  obs
X-squared = 0.3, df = 3, p-value = 1
mendel$expected
[1] 77.62 25.88 25.88  8.62
  • Es gibt keinen Unterschied zwischen den beobachteten und erwarteten Werten (\chi^2 = 0.254, df = 3, p = 0.97).

Unabhängigkeitstest: Vergleich von 2 oder mehr Merkmalen

Kontingenztafeln

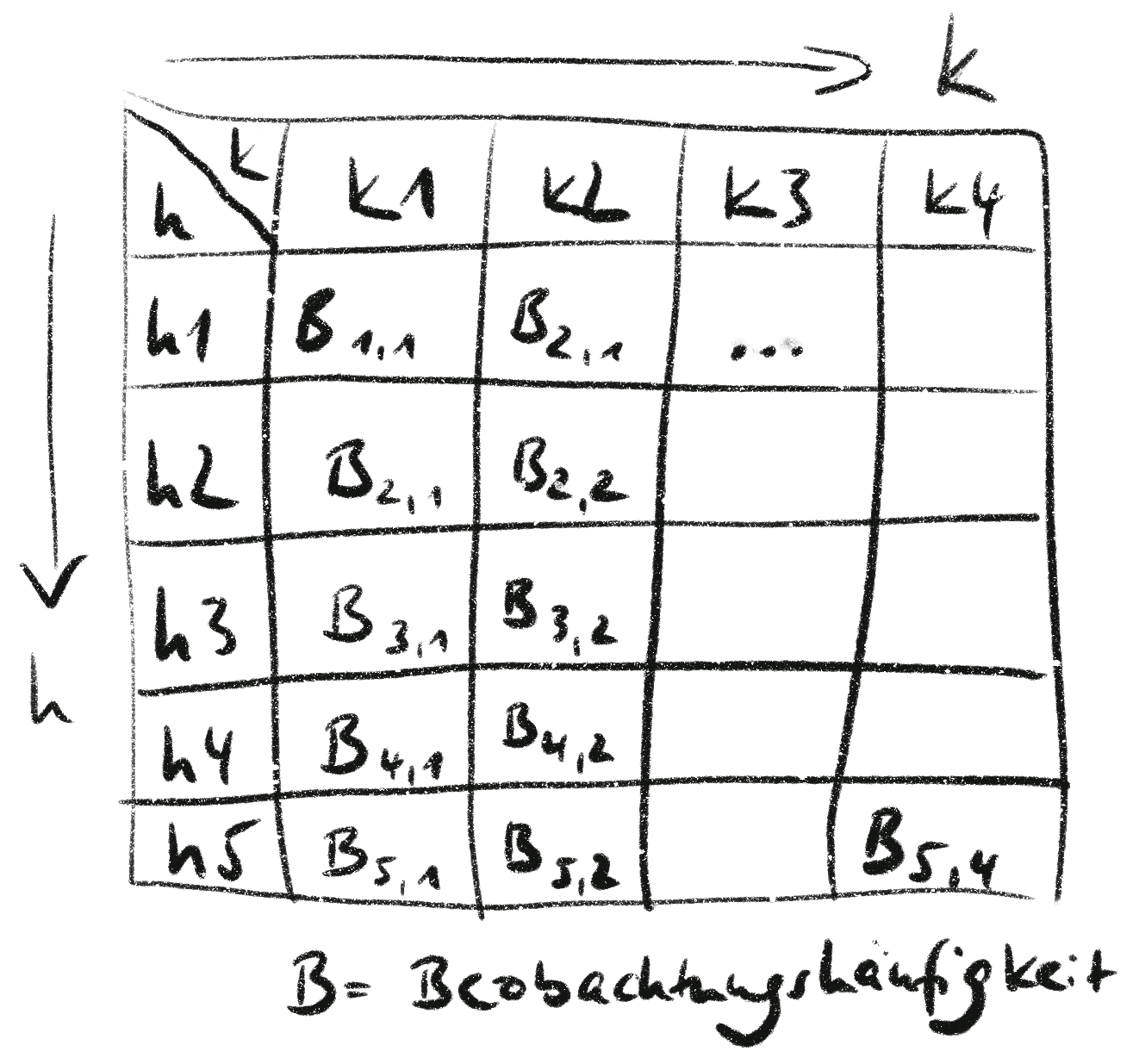
  • 1 Merkmal: Einfach-Klassifizierung → nur 1 Zeile bzw. Spalte
  • 2 Merkmale: Zweifach-Klassifizierung → h Zeilen und k Spalten mit (h-1)(k-1) Freiheitsgraden
  • In der Statistik sind Kontingenzen alle Ereignisse, die möglicherweise eintreten können.
  • Eine Kontingenztafel zeigt die Anzahl, wie oft jede der Kontingenzen in einer bestimmten Stichprobe tatsächlich beobachtet wurde.

Pearsons Chi-Quadrat-Test

Beispiel: COVID-19-Impfstoffabdeckung bei Mitarbeitern des Gesundheitswesens in England

Sind Mitarbeiter des Gesundheitswesens, die keine COVID-19 Vorerkrankung hatten, verstärkt geimpft worden?

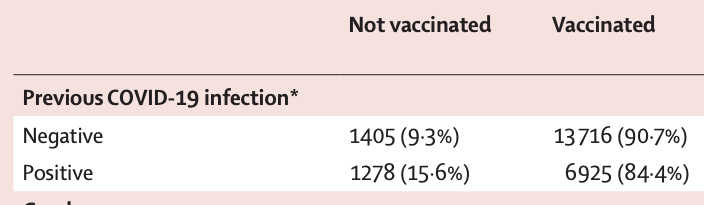
H0: Es gibt keinen Zusammenhang zwischen der Impfrate und COVID-19 Vorerkrankungen, die Verteilungen in beiden Merkmalen sind unabhängig voneinander.

Artikel: Hall et al., 2021, The Lancet

Beispiel: COVID-19-Impfstoffabdeckung | Daten

Beobachtungswerte (aus Tabelle 1)

COVID-19 Vorerkrankung Nicht Geimpft Geimpft Gesamt
Negativ 1405 13716 15121
Positiv 1278 6925 8203
Gesamt 2683 20641 23324

Beispiel: COVID-19-Impfstoffabdeckung | Wahrscheinlichkeiten 1

COVID-19 Vorerkr. Nicht Geimpft Geimpft Gesamt
Negativ P(neg. \cap nicht~geimpft) P(neg. \cap geimpft) 15121
Positiv P(positiv \cap nicht~geimpft) P(positiv \cap geimpft) 8203
Gesamt 2683 20641 23324
  • Unter der H0 sollte die spezielle Multiplikationsregel (Regel 5) angewendet werden können, sprich Ereignisse A und B sind voneinander unabhängig → P(A \cap B) = P(A)*P(B)
  • Nun müssen die Wahrscheinlichkeiten nur noch aus den Randhäufigkeiten ermittelt werden, z.B:
    • 15121 von insgesamt 23324 hatten keine Vorerkrankung → P(negativ)=\frac{15121}{23324}= 0.648
    • 20641 von insgesamt 23324 wurden geimpft → P(geimpft)=\frac{20641}{23324}= 0.885
    • Somit ist P(negativ \cap geimpft) = \frac{15121}{23324}*\frac{20641}{23324} = 0.5737269

Beispiel: COVID-19-Impfstoffabdeckung | Wahrscheinlichkeiten 2

COVID-19 Vorerkr. Nicht Geimpft Geimpft Gesamt
Negativ \frac{15121}{23324}*\frac{2683}{23324} = 0.0746 \frac{15121}{23324}*\frac{20641}{23324} = 0.5737 15121
Positiv \frac{8203}{23324}*\frac{2683}{23324} = 0.0404 \frac{8203}{23324}*\frac{20641}{23324} = 0.3112 8203
Gesamt 2683 20641 23324
  • Der Erwartungswert ist entsprechend E = P * N

Beispiel: COVID-19-Impfstoffabdeckung | Erwartungswerte

COVID-19 Vorerkr. Nicht Geimpft Geimpft Gesamt
Negativ 0.0746*N \approx 1740 0.5737*N \approx 13381 15121
Positiv 0.0404*N \approx 943 0.3112*N \approx 7260 8203
Gesamt 2683 20641 23324 (N)
  • Wichtig ist, dass die Randhäufigkeiten für Erwartungs- und Beobachtungswerte erhalten bleiben: kontingent heißt auch ‘abhängig von’ oder ‘bedingt durch’.
  • Die Formel lässt sich sogar noch verkürzen: E_{negativ, nicht~geimpft} = \frac{Zeilensumme* Spaltensumme}{Gesamtsumme} = \frac{15121*2683}{23324}

Beispiel: COVID-19-Impfstoffabdeckung | Berechnung

Manuell (\chi^2 und G)

obs <- c(1405, 13716, 1278, 6925)
exp <- c(1740, 13381, 943, 7260)
(chi2 <- sum((obs - exp)^2/exp) )
[1] 207
(g <- 2*sum((obs*log(obs/exp))) )
[1] 200
qchisq(p = 0.95, df = (2-1)*(2-1))
[1] 3.84
pchisq(chi2, df = 1, lower.tail = FALSE)
[1] 5.2e-47
pchisq(g, df = 1, lower.tail = FALSE)
[1] 1.99e-45

Built-in Funktion (\chi^2)

obs <- matrix(obs, byrow = TRUE, nrow = 2)
covid <- chisq.test(obs, correct = FALSE)
covid

    Pearson's Chi-squared test

data:  obs
X-squared = 207, df = 1, p-value <2e-16
covid$expected
     [,1]  [,2]
[1,] 1739 13382
[2,]  944  7259

Freiheitsgrade hier: (Anzahl Zeilen der Kontingenztafel - 1)*(Anzahl Spalten der Kontingenztafel - 1)

Voraussetzungen

beim Pearsons Chi-Quadrat-Test (und G-Test)

  • Es können nur Häufigkeitsverteilungen getestet werden, keine Proportionen oder Prozentsätze.
  • Alle Erwartungswerte sollten mind. ≥ 2 sein, mindestens 80% sollten ≥ 5 sein.
    • \chi^2 reagiert bei kleinen Erwartungswerten sehr empfindlich auf kleine Abweichungen.
    • Dadurch zunehmende Gefahr eines statistischen Fehler 2. Art.
  • Errechneter \chi^2-Wert basiert auf beschränkten Datenmengen, wird aber zur Signifikanz mit kontinuierlichen Verteilung verglichen
    • Bei kleinen Stichproben (N<20) empfielt sich Stetigkeitskorrektur nach Yates (Standardeinstellung in R mit correct = TRUE)

\chi^2_{korrigiert} = \sum\frac{(|B_i-E_i|-0.5)^2}{E_i}

Stetigkeitskorrektur nach Yates | COVID-19 Bsp.

Vergleich

chisq.test(obs, correct = FALSE)

    Pearson's Chi-squared test

data:  obs
X-squared = 207, df = 1, p-value <2e-16
chisq.test(obs) # correct = TRUE

    Pearson's Chi-squared test with Yates' continuity correction

data:  obs
X-squared = 206, df = 1, p-value <2e-16
  • Nachteil der Korrektur soll allerdings sein, dass Werte konservativ sind (p-Werte sind tendenziell höher) → einige empfehlen daher nur bei df = 1 die Korrektur.

Your turn …

03:00

Quiz zum Nachmachen | Kelchblattbreite

Ausgangssituation

Die Messungen der Kelchblattbreite im iris Datensatzes lassen sich in folgende drei Größenklassen einteilen:

Code 
df <- iris |>
  # Mit cut() können wir eine metrische Variable kategorial machen:
  mutate(sw_class = cut(Sepal.Width, breaks = 3) ) |>
  group_by(Species, sw_class) |>
  # shortuct für summarise(n = n())
  count() |>
  pivot_wider(names_from = Species, values_from = n, 
    values_fill = 0)
df$sw_class <- c("< 2.8 cm", "2.8-4 cm", "> 4 cm")

sw_sizeclass <- as.matrix(df[ ,2:4])
rownames(sw_sizeclass) <- df$sw_class

knitr::kable(df, format = "html", col.names = c(
  "Größenklasse", "I. setosa", "I. versicolor", "I. virginica")) |>
  kableExtra::kable_styling(position = "center", font_size = 20)
Größenklasse I. setosa I. versicolor I. virginica
< 2.8 cm 1 27 19
2.8-4 cm 36 23 29
> 4 cm 13 0 2

Pearson Chi-Quadrat

Nun wird ermittelt, ob das Größenmerkmal und die Artzugehörigkeit voneinander abhängen:

chisq.test(x = sw_sizeclass)

    Pearson's Chi-squared test

data:  sw_sizeclass
X-squared = 45, df = 4, p-value = 4e-09
chisq.test(x = sw_sizeclass)$expected
         setosa versicolor virginica
< 2.8 cm   15.7       15.7      15.7
2.8-4 cm   29.3       29.3      29.3
> 4 cm      5.0        5.0       5.0

Quiz zum Nachmachen | Frage 1

Pearson Chi-Quadrat

Nun wird ermittelt, ob das Größenmerkmal und die Artzugehörigkeit voneinander abhängen:

chisq.test(x = sw_sizeclass)

    Pearson's Chi-squared test

data:  sw_sizeclass
X-squared = 45, df = 4, p-value = 4e-09
chisq.test(x = sw_sizeclass)$expected
         setosa versicolor virginica
< 2.8 cm   15.7       15.7      15.7
2.8-4 cm   29.3       29.3      29.3
> 4 cm      5.0        5.0       5.0

Quiz zum Nachmachen | Frage 2

Pearson Chi-Quadrat

Nun wird ermittelt, ob das Größenmerkmal und die Artzugehörigkeit voneinander abhängen:

chisq.test(x = sw_sizeclass)

    Pearson's Chi-squared test

data:  sw_sizeclass
X-squared = 45, df = 4, p-value = 4e-09
chisq.test(x = sw_sizeclass)$expected
         setosa versicolor virginica
< 2.8 cm   15.7       15.7      15.7
2.8-4 cm   29.3       29.3      29.3
> 4 cm      5.0        5.0       5.0

Quiz zum Nachmachen | Frage 3

Pearson Chi-Quadrat

Nun wird ermittelt, ob das Größenmerkmal und die Artzugehörigkeit voneinander abhängen:

chisq.test(x = sw_sizeclass)

    Pearson's Chi-squared test

data:  sw_sizeclass
X-squared = 45, df = 4, p-value = 4e-09
chisq.test(x = sw_sizeclass)$expected
         setosa versicolor virginica
< 2.8 cm   15.7       15.7      15.7
2.8-4 cm   29.3       29.3      29.3
> 4 cm      5.0        5.0       5.0

Exakter Test nach Fisher

Alternativen, wenn Voraussetzung nicht erfüllt ist

Was tun, wenn beim Pearson’s \chi^2-Test oder beim G-Test zu viele der erwarteten Häufigkeiten <5 sind?

  1. Klassen zusammenfassen
  2. Exakter Test nach Fisher (Fisher’s Exact Test)

Exakter Test nach Fisher

  • Von Ronal A. Fisher 1934 der Royal Statistical Society vorgestellt → kam allerdings zu der Zeit nicht an.
  • Heute allgemeingültiger Ansatz der gerade bei kleinen bis mittelgroßen Stichproben genutzt wird.
  • Bei großen Stichproben (> 500) soll sich das Verfahren asymptotisch einem \chi^2-Test mit einem FG annähern.
  • Mit diesem Permutationstest können exakte p-Werte berechnet werden (der Pearson’s \chi^2- sowie G-Test sind nur Annäherungen).

Exakter Test nach Fisher | Wahrscheinlichkeit

Merkmale M1 und M2 + - Summe
+ a b a + b
- c d c + d
Summe a + c b + d a + b + c + d = n

Die Wahrscheinlichkeit für ein bestimmtes Ergebnis ist gegeben durch

p=\frac{(a+b)!(c+d)!(a+c)!(b+d)!}{a!b!c!d!n!}

Bsp: Habitatpräferenz | Daten & Wahrscheinlichkeit

Unterscheiden sich zwei Tannenhäher- und Eichelhäherarten in ihrer Häufigkeit in verschiedenen Waldtypen?

Beobachtungen

Waldtyp Tannenhäher Eichelhäher Summe
Nadelwald 6 2 8
Laubwald 4 8 12
Summe 10 10 20 
Wahrscheinlichkeit für dieses 'Ereignis'
( factorial(8)*factorial(12)*factorial(10)*factorial(10) ) /
  ( factorial(6)*factorial(2)*factorial(4)*factorial(8)*factorial(20) )
[1] 0.075

Wir sind aber noch nicht fertig!!!

Bsp: Habitatpräferenz | Wahrscheinlichkeit extremer Werte

Wir müssen die Wahrscheinlichkeit von Ergebnissen berechnen, die noch extremer sind als dieses. Es gibt zwei davon (bei gleichen Randsummen):

Ergebnisvariante 1

Waldtyp TH EH Summe
Nadelwald 7 1 8
Laubwald 3 9 12
Summe 10 10 20 
P von Ergebnisvariante 1
( factorial(8)*factorial(12)*
    factorial(10)*factorial(10) ) /
( factorial(7)*factorial(1)*factorial(3)*
      factorial(9)*factorial(20) )
[1] 0.00953

Ergebnisvariante 2

Waldtyp TH EH Summe
Nadelwald 8 0 8
Laubwald 2 10 12
Summe 10 10 20 
P von Ergebnisvariante 2
( factorial(8)*factorial(12)*
    factorial(10)*factorial(10) ) /
( factorial(8)*factorial(0)*factorial(2)*
      factorial(10)*factorial(20) )
[1] 0.000357

Bsp: Habitatpräferenz | Ergebnis

Diese 3 Wahrscheinlichkeiten müssen nun addiert werden und dann mit 2 multipliziert werden für einen 2-seitigen Test:

Berechnung der finalen Wahrscheinlichkeit
2 * (0.075 + 0.00953 + 0.000357)
[1] 0.17

Shortcut: Die built-in Funktion fisher.test()

mat <- matrix(c(6,2,4,8), byrow = TRUE, nrow = 2)
fisher.test(mat)

    Fisher's Exact Test for Count Data

data:  mat
p-value = 0.2
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
  0.603 79.831
sample estimates:
odds ratio 
      5.43

Fragen?

Abschlussquiz

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de

Creative Commons License
Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.

Kurswebseite: Data Science 2