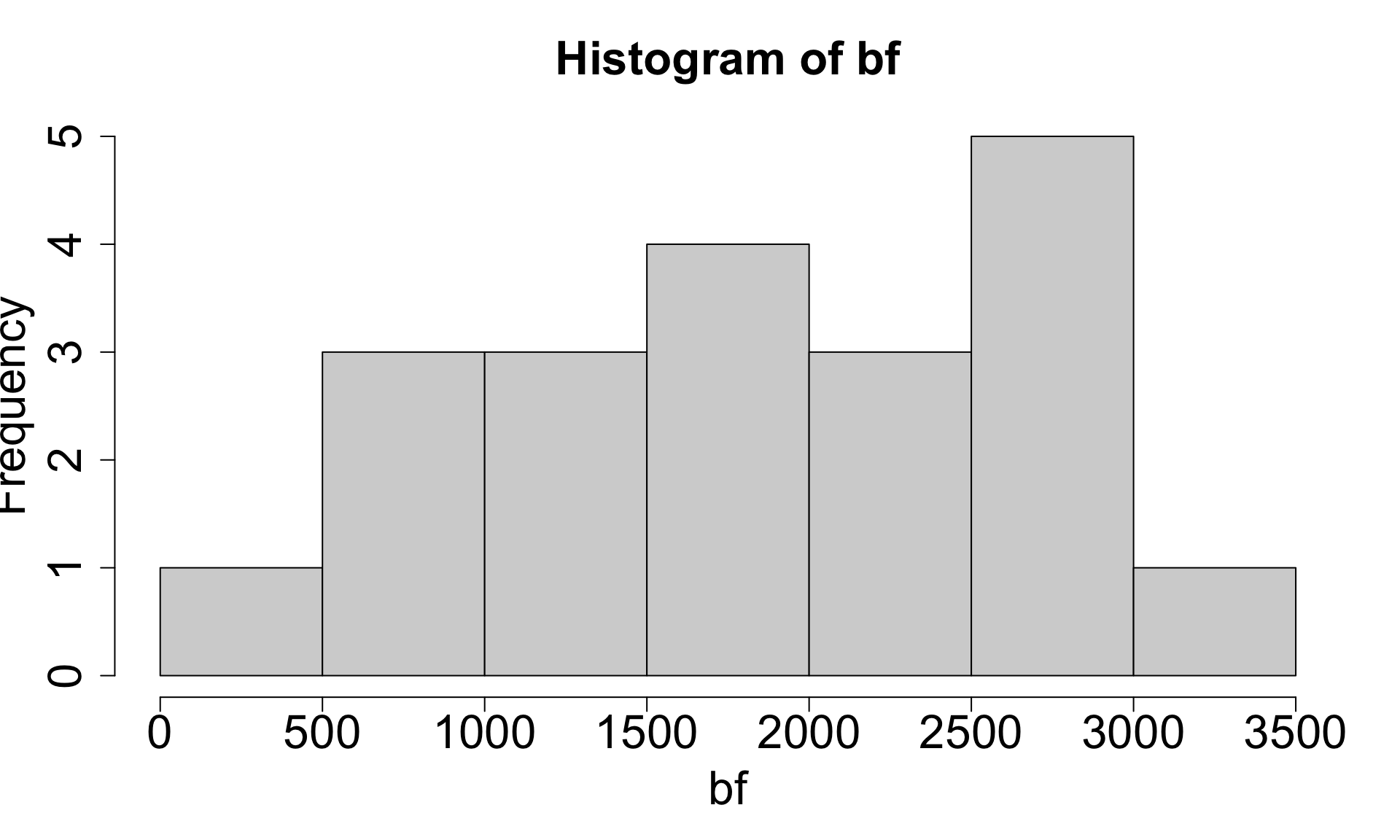
6-Klassische Tests zum Prüfen auf Unterschiede: metrische/ordinale Daten

Data Science 2

Saskia Otto & Monika Eberhard

Universität Hamburg, IMF & IZS

Sommersemester 2025

Lernziele

Nach Abschluss dieser VL und Übung..

• können Sie auf Unterschiede zwischen zwei Mittelwerten für unabhängige UND gepaarte Stichproben testen.
• wissen sie wann sie den parametrische t-Test verwenden können und wann besser den nicht-parametrischen Mann-Whitney U-Test bzw. Wilcoxon-Vorzeichen-Rang-Test.

Heutige Fragen

Unterscheidet sich das durchschnittliche Zugverhalten zwischen Buchfinken und Mönchsgrasmücken?

Buchfink

Mönchsgrasmücke

Männliche Kohlmeise

Singen Kohlmeisen in der Stadt durchschnittlich lauter als auf dem Land?

Bildquellen rechts oben: Wikipedia (Buchfink unter (CC BY-SA 2.5 Lizenz) und Mönchsgrasmücke unter CC0 Lizenz)

Bildquelle links unten: Luc Viator-Wikimedia (CC-BY-SA 2.0 Lizenz)

t-Test: Parametrischer Ein- und Zweistichprobentest

Mittelwertvergleich bei metrischen Daten

Zur Erinnerung

Parametrische Tests

• Verteilungsabhängig
• Arbeiten mit \bar{X}, s^2, s
• Nur für metrische Daten
• Annahmen:
  1. Unabhängigkeit (außer gepaarter t-Test)
  2. Varianzhomogenität (gleiche Varianzen)
  3. Normalität (Normalverteilung)

• Tests:
  • F-Test,
  • t-Test für 1 und 2 Stichproben
  • Varianzanalyse (ANOVA), Kovarianzanalyse (ANCOVA)
    
  • Pearson Produkt-Moment-Korrelationskoeffizient, lineare Regression

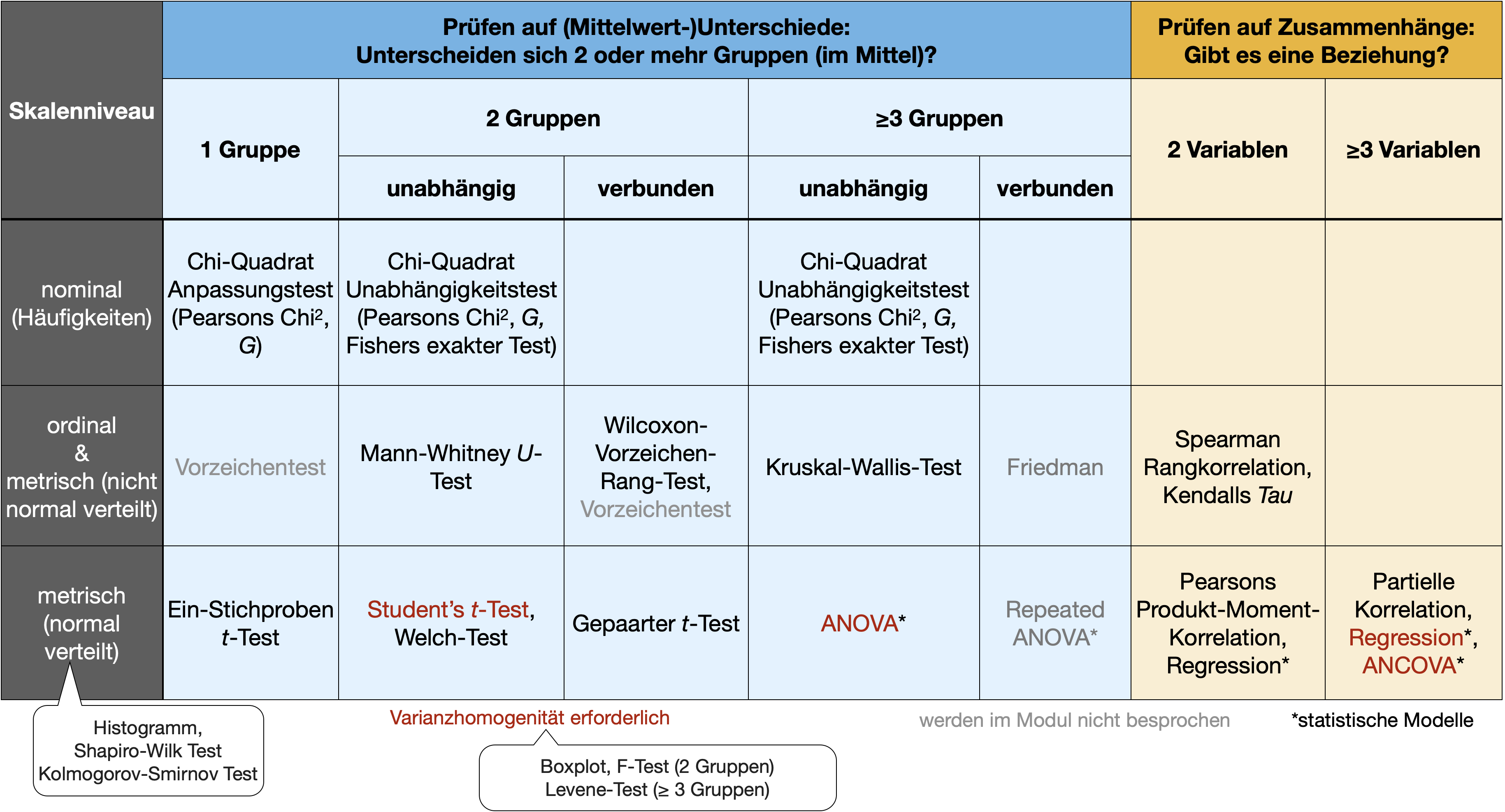
Prüfen der Annahmen

• Schritt 1 - Normalverteilung:
  • Grafisch: Histogramm, Boxplot
  • Test: Shapiro-Wilk-Test
• Schritt 2 - Varianzhomogenität:
  • Grafisch: Boxplot
  • Test: F-Test

t-Test in R

Built-in Funktion t.test()

t.test(x, y = NULL,
       alternative = c("two.sided", "less", "greater"),
       mu = 0, paired = FALSE, var.equal = FALSE,
       conf.level = 0.95, ...)

t-Test für 1 Stichprobe

• Hier wird getestet, ob sich der Mittelwert einer einzelnen Stichprobe von einem vorgegebenen Populationsmittelwert \mu_0 unterscheidet.
• Die Teststatistik t folgt einer t-Verteilung.

Formel der Kenngröße t

t=\frac{\bar{X}-\mu_0}{s_{\bar{X}}}=\frac{\bar{X}-\mu_0}{\frac{s}{\sqrt{n}}}\Rightarrow~~\text{wenn}~\mu_0 = 0: \frac{\bar{X}}{\frac{s}{\sqrt{n}}}

• \bar{X} = Stichprobenmittelwert
• \mu_0 = theoretischer Populationsmittelwert
• s_{\bar{X}} = Standardschätzfehler des Mittelwerts

Hypothesen

• zweiseitig:
  • H_0: \mu = \mu_0
  • H_A: \mu \neq \mu_0
• linksseitig:
  • H_0: \mu \geq \mu_0
  • H_A: \mu < \mu_0
• rechtsseitig:
  • H_0: \mu \leq \mu_0
  • H_A: \mu > \mu_0

t-Test für 1 Stichprobe | Bsp. Zugverhalten 1

Forschungsfrage

Unterscheidet sich unsere Stichprobe zum Zugverhalten des Buchfinks (BF1) von einer anderen Stichprobe (BF2), für die wir nur den Mittelwert kennen?

Bekannte Statistiken

Kenngröße	BF1	BF2
Mittelwert \bar{X}	1800 km	1697 km
Standardabw. s	±900 km	?
Stichprobengröße n	20	?

Die 8 Schritte

Kennwert:	\mu bzw. \bar{X}
H0:	BF1 = BF2
HA:	BF1 \neq BF2
Voraussetzung:	Normalverteilung
Teststatistik:	t
alpha:	0.05
FG:	n-1 = 19
p-Wert:	Vergleich t-Wert mit t_{krit} aus einer t-Verteilung

Bildquelle: Wikipedia (CC BY-SA 2.5 Lizenz)

t-Test für 1 Stichprobe | Bsp. Zugverhalten 2

Die Daten

bf

 [1]  697.6 1619.2  743.0 1065.2 1177.8   26.5 2764.1 2021.9  621.4 3215.2
[11] 2318.1 1535.6 2826.3 2807.8 2746.5 2602.4 2456.3 1788.5 1523.8 1443.0

Empirische Verteilung

hist(bf)

Prüfen auf Normalverteilung

shapiro.test(bf)

    Shapiro-Wilk normality test

data:  bf
W = 1, p-value = 0.5

t-Test für 1 Stichprobe | Bsp. Zugverhalten 3

Manuelle Berechnung

mean_x <- mean(bf)
mu0 <- 1697
n <- 20
se_x <- sd(bf)/sqrt(n)
# Berechnung des t-Werts
t_val <- (mean_x - mu0) / se_x
t_val

[1] 0.512

# Kritischer t-Wert
qt(p = 0.025, df = 19, lower.tail=F)

[1] 2.09

# P für berechneten t-Wert mal 2
# (weil zweiseitige H0)
pt(t_val, df=19, lower.tail=F) * 2

[1] 0.615

Built-in Funktion

t.test(x = bf, mu = 1697, 
  alternative = "two.sided")

    One Sample t-test

data:  bf
t = 0.5, df = 19, p-value = 0.6
alternative hypothesis: true mean is not equal to 1697
95 percent confidence interval:
 1379 2221
sample estimates:
mean of x 
     1800 

t-Test für 1 Stichprobe | Bsp. Zugverhalten 4

• Die Teststatistik t liegt zwischen dem unteren und oberen t_{krit}, somit kann die H_0 nicht verworfen werden.
• Anders ausgedrückt:
  • Die Wahrscheinlichkeit ein statistisches Ergebnis wie das beobachtete zu erhalten, wenn die Nullhypothese wahr wäre, liegt bei 61.5%.
  • Somit können wir die H_0 nicht ablehnen (erst bei <5%).

Built-in Funktion

t.test(x = bf, mu = 1697, 
  alternative = "two.sided") # default

    One Sample t-test

data:  bf
t = 0.5, df = 19, p-value = 0.6
alternative hypothesis: true mean is not equal to 1697
95 percent confidence interval:
 1379 2221
sample estimates:
mean of x 
     1800 

ZUSAMMENFASSUNG: → Es gibt keinen signifikanten Unterschied zwischen unserer Stichprobe und der Vergleichsstichprobe (t = 0.51, df = 19, p > 0.5).

t-Test bei 2 unabhängigen Stichproben | 1

Student’s t-Test bei GLEICHEN Varianzen

• Der am häufigsten verwendete Zweistichproben-Test.
• Der Stichprobenumfang beider Gruppen darf ungleich sein.
• Theoretisch kann der t-Test auch bei sehr kleinen Stichprobenumfängen (z. B. 10) verwendet werden.
• Testet die Nullhypothese, dass die Mittelwerte von zwei Populationen gleich sind:
  • H_0: \mu_1 = \mu_2 bzw. \mu_1-\mu_2=0

t-Test bei 2 unabhängigen Stichproben | 2

Student’s t-Test bei GLEICHEN Varianzen

Formel der Kenngröße t

t=\frac{(\bar{X}_1-\bar{X}_2) -(\mu_1 - \mu_2)}{s_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \Rightarrow~~\text{wenn}~~\mu_1-\mu_2=0:~t = \frac{(\bar{X}_1-\bar{X}_2)}{s_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}

s_p = \text{Standardabweichung der gepoolten Stichprobe:}

s_p = \sqrt{\frac{(n_1-1)s_1^2 + (n_2 -1)s_2^2}{(n_1-1) + (n_2-1)}} \text{wenn } n \text{ identisch ist: }s_p = \sqrt{\frac{s_1^2 + s_2^2}{2}}

t-Test bei 2 unabhängigen Stichproben | 3

Welch’s t-Test bei UNGLEICHEN Varianzen

• Was ist, wenn die Varianzen nicht gleich sind?
  • → gepoolte Schätzung der Standardabweichung ungeeignet
  • → t-Verteilung mit (n_1-1)+(n_2-1) Freiheitsgraden keine gute Annäherung an die Stichprobenverteilung
• Anpassung der Teststatistik t und der Freiheitsgrade:

Formel der Kenngröße t

t=\frac{(\bar{X}_1-\bar{X}_2) -(\mu_1 - \mu_2)}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}

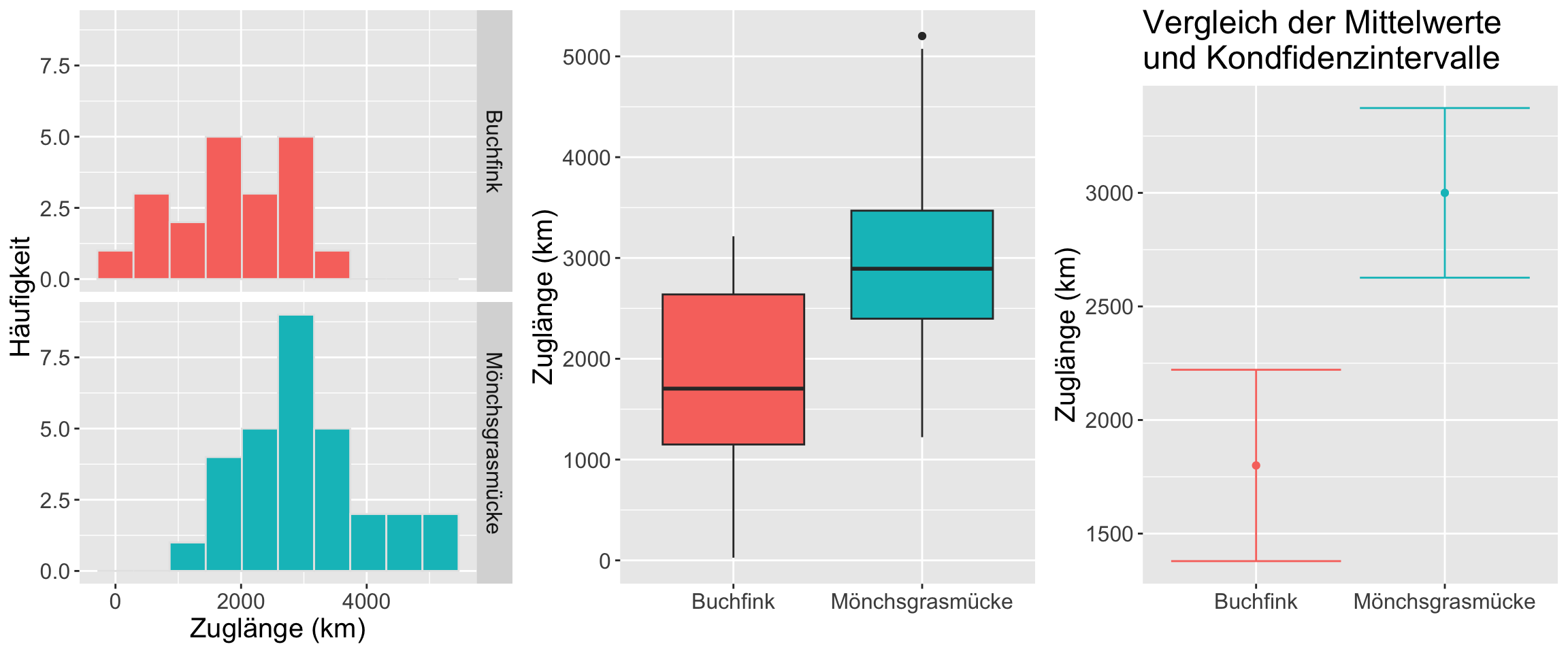
Bsp. Buchfinken vs. Mönchsgrasmücken | 1

Unterscheidet sich das durchschnittliche Zugverhalten zwischen Buchfinken und Mönchsgrasmücken?

Buchfink

Mönchsgrasmücke

Kenngröße	Buchfink	Mönchsgrasmücke
Mittelwert x̅	1800 km	3000 km
Standardabweichung s	±900 km	±1000 km
Stichprobengröße n	20	30

Bildquellen: Wikipedia (Buchfink unter (CC BY-SA 2.5 Lizenz) und Mönchsgrasmücke unter CC0 Lizenz)

Bsp. Buchfinken vs. Mönchsgrasmücken | 2

Testen der Annahmen

• Grafische Exploration
• Normalität
• Varianzhomogenität

shapiro.test(bf)

    Shapiro-Wilk normality test

data:  bf
W = 1, p-value = 0.5

shapiro.test(mgm)

    Shapiro-Wilk normality test

data:  mgm
W = 1, p-value = 0.6

→ Die H0 wird jeweils angenommen, da p > 0.05: beide Stichproben sind normal verteilt.

var.test(x = bf, y = mgm)

    F test to compare two variances

data:  bf and mgm
F = 0.8, num df = 19, denom df = 29, p-value = 0.6
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.363 1.946
sample estimates:
ratio of variances 
              0.81 

→ Die H0 wird angenommen, da p > 0.05: die Varianzen beider Gruppen sind gleich.

Bsp. Buchfinken vs. Mönchsgrasmücken | 3

Kennwert:	\mu bzw. \bar{X}
H0:	\mu_{BF} = \mu_{MGM}
HA:	\mu_{BF} \neq \mu_{MGM}
Voraussetzung:	Normalität/Varianzhomogenität
Teststatistik:	t = \frac{(\bar{X}_{BF}-\bar{X}_{MGM})}{s_p \sqrt{\frac{1}{n_{BF}} + \frac{1}{n_{MGM}}}}
alpha:	0.05
FG:	(n_{BF}-1)+(n_{MGM}-1) = 19+29 = 48
p-Wert:	Vergleich t-Wert mit t_{krit} aus einer t-Verteilung

Student’s t-Test

t.test(x = bf, y = mgm, var.equal = TRUE)

    Two Sample t-test

data:  bf and mgm
t = -4, df = 48, p-value = 8e-05
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -1758  -642
sample estimates:
mean of x mean of y 
     1800      3000 

• Da der p-Wert mit 0.00008 < alpha (0.05) ist, kann die H_0 abgelehnt werden.
• Die Zuglänge ist bei Buchfinken signifikant kleiner als bei Mönchsgrasmücken (t = -4.3, df = 48, p < 0.001).

Bsp. Buchfinken vs. Mönchsgrasmücken | 4

Manuelle Berechnung

Zur Erinnerung: t = \frac{(\bar{X}_1-\bar{X}_2)}{s_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}\text{ mit }s_p = \sqrt{\frac{(n_1-1)s_1^2 + (n_2 -1)s_2^2}{(n_1-1) + (n_2-1)}}

s_pooled <- sqrt( (19*var(bf) + 29*var(mgm)) / (19 + 29) )
t_val <- (mean(bf) - mean(mgm)) / (s_pooled * sqrt(1/20 + 1/30))
t_val

[1] -4.32

# Weil t_val negativ ist, wird lower.tail=TRUE gesetzt
pt(t_val, df = 19+29, lower.tail = TRUE)*2 

[1] 0.0000773

Wenn Stichproben abhängig sind

Abb. links: Fotoaufnahmen des Lake Powell, USA, am Zusammenfluss mit dem Dirty Devil River (Quelle: https://pubs.usgs.gov/fs/2004/3062/)

• Abhängigkeit entsteht z.B. durch
  • Messwiederholung der gleichen Stichprobe (vor und nach einer Behandlung, Stichproben in zwei verschiedenen Jahren usw.),
  • wenn Paare auf zwei Gruppen aufgeteilt werden (es wird z.B. der Größenunterschied zwischen weiblichen und männlichen Schwänen untersucht, aber nur Paare beprobt).

Gepaarter t-Test | 1

2 abhängige Stichproben

• Testet die Nullhypothese, dass die Differenz zwischen den gepaarten Beobachtungen Null ist:
  • H_0: d = \mu_1-\mu_2 = 0

Vorgehensweise

1. Berechnung der Differenzen der gepaarten Beobachtung.
2. Berechnung des Mittelwerts und des Standardschätzfehlers aus diesen Differenzen.

Formel der Kenngröße

t = \frac{\bar{d}-\mu_d}{s_{\bar{d}}} = \frac{\bar{d}-\mu_d}{\frac{s}{\sqrt{n}}}

\text{mit }FG = n-1

Bsp. Pharmazeutische Schlafstudie | 1

Daten, die die Wirkung von zwei einschläfernden Medikamenten (Zunahme der Schlafstunden im Vergleich zur Kontrolle) bei 10 Patienten zeigen.

Patient	Medikament1	Medikament2	Differenz
1	0.7	1.9	-1.2
2	-1.6	0.8	-2.4
3	-0.2	1.1	-1.3
4	-1.2	0.1	-1.3
5	-0.1	-0.1	0.0
6	3.4	4.4	-1.0
7	3.7	5.5	-1.8
8	0.8	1.6	-0.8
9	0.7	4.6	-3.9
10	2.0	3.4	-1.4

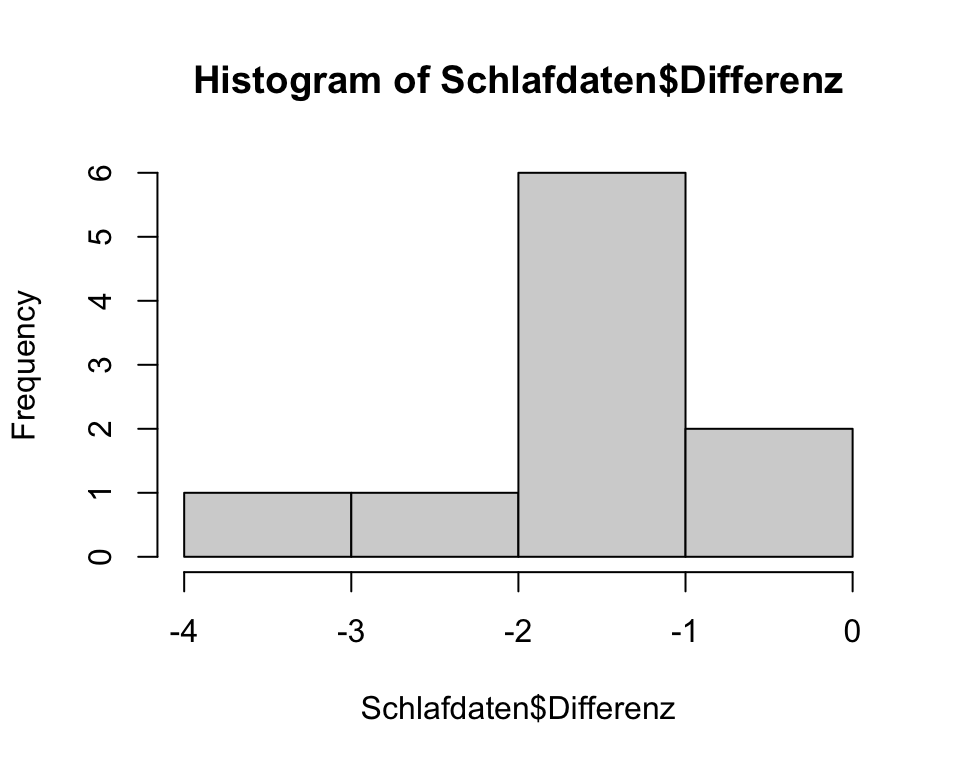
Bsp. Pharmazeutische Schlafstudie | 2

Prüfung auf Normalverteilung

• Da sich der gepaarte t-Test auf die paarweisen Differenzen bezieht, muss diese normal verteilt sein!
• Die Varianzhomogeniät zwischen den beiden Gruppen fällt entsprechend weg.

hist(Schlafdaten$Differenz)

shapiro.test(Schlafdaten$Differenz)

    Shapiro-Wilk normality test

data:  Schlafdaten$Differenz
W = 0.9, p-value = 0.2

→ Die Stichprobe der Differenzen ist normal verteilt (p-Wert > 0.05).

Bsp. Pharmazeutische Schlafstudie | 3

Anwendung des gepaarten t-Tests

t.test(x = Schlafdaten$Medikament1, 
       y = Schlafdaten$Medikament2, 
       paired = TRUE)

    Paired t-test

data:  Schlafdaten$Medikament1 and Schlafdaten$Medikament2
t = -5, df = 9, p-value = 0.001
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 -2.258 -0.762
sample estimates:
mean difference 
          -1.51 

• Da der p-Wert < 0.05 ist, kann die H_0 abgelehnt werden.
• → Es gibt einen sign. Unterschied in der Wirksamkeit zwischen den beiden Medikamenten (t = -4.06, FG = 9, p = 0.003). Im Durchschnitt schliefen die Probanden 1.58 Stunden länger mit Medikament 2.

Bsp. Pharmazeutische Schlafstudie | 4

Vergleich zum 1-Stichproben t-Test

• Im gepaarten t-Test betrachten wir eigentlich nur eine Stichprobe - die der Differenzen.
• Die gemittelte Differenz wird dann gegen den Referenzwert Null verglichen (zur Erinnerung: H_0: d = \mu_1-\mu_2 = 0).
• Somit erhalten wir das gleiche Ergebnis, wenn wir den 1-Stichproben t-Test mit der Differenz Vektor und einem mu von 0 durchführen:

t.test(x = Schlafdaten$Differenz, mu = 0) 

    One Sample t-test

data:  Schlafdaten$Differenz
t = -5, df = 9, p-value = 0.001
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -2.258 -0.762
sample estimates:
mean of x 
    -1.51 

Übersicht der t-Test Anwendungen

• Einstichproben t-Test, zweiseitige Hypothese (Standard):
  • t.test(x, mu)
• Unabhängiger Zweistichproben-t-Test (gleiche Varianzen), zweiseitig: H_A:µ1 ≠ µ2
  • t.test(x, y, var.equal = TRUE)
• Unabhängiger Zweistichproben-t-Test (gleiche Varianzen), einseitig: H_A:µ1 > µ2:
  • t.test(x, y, var.equal = TRUE, alternative = “greater”)
• Welch-Test (ungleiche Varianzen = default), einseitig: H_A:µ1 < µ2
  • t.test(x, y, alternative = “less”)
• Gepaarter Zweistichproben-t-Test (gleiche Varianzen) , zweiseitige Hypothese:
  • t.test(x, y, paired = TRUE, var.equal = TRUE)
• Gepaarter t-Test mit 2 Stichproben (ungleiche Varianzen) , einseitig: H_A:µ1 > µ2
  • t.test(x, y, paired = TRUE, alternative = “greater”)

Übersicht der Hypothesen bei den t-Tests

Your turn …

03:00

Quiz 1 | Testwahl

Kelchblattlänge in iris

Ausgangssituation:

• Es soll die Hypothese getestet werden, dass die durchschnittliche Kelchblattlänge der Art Iris setosa kleiner ist als bei der Art Iris virginica.
• Beide Stichproben sind normal verteilt (jeweils W = 0.97, p > 0.05).
• Die Varianzen beider Stichproben sind signifikant unterschiedlich (F_{(49,49)}=3.25, p < 0.001).

Quiz 2 | Funktionsaufruf

Kelchblattlänge in iris

set <- iris$Sepal.Length[iris$Species=="setosa"]
vir <- iris$Sepal.Length[iris$Species=="virginica"]

Quiz 3 | Interpretation

Kelchblattlänge in iris

Testergebnis

t.test(x=set, y=vir, alternative='less')

    Welch Two Sample t-test

data:  set and vir
t = -15, df = 77, p-value <2e-16
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
  -Inf -1.41
sample estimates:
mean of x mean of y 
     5.01      6.59 

Nicht-Parametrische Tests - Teil 1

Vergleich zweier Stichproben mit ordinalen und metrischen (nicht normal verteilten) Daten

Zur Erinnerung

Nicht-Parametrische Tests

• Verteilungsfrei (keine Normalverteilung erforderlich)
• Arbeiten mit Median und Rängen
• Für ordinale, und nominale Daten
• Metrische Daten → Transformation in Rangdaten (ordinale Daten)
• Teststärke ist allgemein niedriger
• Nicht geeignet bei komplexem Design

• Tests:
  • → Mann-Whitney U-Test
  • → Wilcoxon-Vorzeichen-Rang-Test
  • Chi-Quadrat-Tests
  • Kruskal-Wallis-Test, Friedman-Test
  • Rangkorrelation (z.B. Spearman, Kendall)
    

Äquivalent zum t-Test

• 2 unabhängige Stichproben
  • Mann-Whitney U-Test
  • = Mann-Whitney-Wilcoxon (MWW)-Test
  • = Wilcoxon Rangsummentest (Wilcoxon Rank Sum Test)
  • Teststärke nur 95% im Vergleich zum unabhängigen Zweistichproben-t-Test

• 2 gepaarte Stichproben
  • Wilcoxon-Vorzeichen-Rang-Test
  • Engl. Wilcoxon Signed Rank Test
  • Teststärke nur 95% im Vergleich zum gepaarten Zweistichproben-t-Test

Beide ‘Wilcoxon’ Tests in R

Built-in Funktion wilcox.test()

wilcox.test(x, y = NULL,
    alternative = c("two.sided", "less", "greater"),
    mu = 0, paired = FALSE, exact = NULL, correct = TRUE,
    conf.int = FALSE, conf.level = 0.95,
    tol.root = 1e-4, digits.rank = Inf, ...)

Mann-Whitney U-Test ist die Standardeinstellung (paired = FALSE).

Mann-Whitney U | Berechnung

1. Bilden der Ränge für die Werte beider Stichproben zusammen¹ (N=m+n).
2. Bilden der Rangsummen für beide Gruppe² (R_x und R_y)
3. Berechnen von U_x und U_y:
   • U_x = m*n+\frac{m(m+1)}{2}-R_x
   • U_y = m*n+\frac{n(n+1)}{2}-R_y oder U_y = m*n-U_x
4. Das kleinere der errechneten U nehmen³: U_{min} = min(U_x, U_y)

1. Bei gleichen Werten werden Rangmittelwerte vergeben.

2. Bei unterschiedlichen Stichprobengrößen sind die Rangsummen auch unterschiedlich.

3. Wenn das errechnete U_{min} kleiner ist, als das für die gewählte Irrtumswahrscheinlichkeit tabellierte U_{krit}, dann unterscheiden sich die beiden Stichproben.

Mann-Whitney U | Berechnung

1. Bilden der Ränge für die Werte beider Stichproben zusammen¹ (N=m+n).
2. Bilden der Rangsummen für beide Gruppe² (R_x und R_y)
3. Berechnen von U_x und U_y:
   • U_x = m*n+\frac{m(m+1)}{2}-R_x
   • U_y = m*n+\frac{n(n+1)}{2}-R_y oder U_y = m*n-U_x
4. Das kleinere der errechneten U nehmen³: U_{min} = min(U_x, U_y)

1. Bei gleichen Werten werden Rangmittelwerte vergeben.

2. Bei unterschiedlichen Stichprobengrößen sind die Rangsummen auch unterschiedlich.

3. Wenn das errechnete U_{min} kleiner ist, als das für die gewählte Irrtumswahrscheinlichkeit tabellierte U_{krit}, dann unterscheiden sich die beiden Stichproben.

Mann-Whitney U | Kohlmeisen Beispiel

Studie

…Great tits in cities sing faster and at a higher pitch compared to their conspecifics dwelling in forests, as reported in this issue by Slabbekoorn and den Boer-Visser [6]. They suggest that the birds changed their songs to make them stand out against the masking traffic noise in urban areas. ..

Bildquelle männliche Kohlmeise: Luc Viator-Wikimedia (CC-BY-SA 2.0 Lizenz)

Kohlmeisen Beispiel | Eigene Erhebung

Ausgangssituation

Vorgehensweise

• Messen von verschiedenen Individuen in der Stadt (m = 6) auf dem Land (n = 5).
• Sehr kleine Stichproben → Normalverteilung schwer testbar.

Fragestellung

• Singen Kohlmeisen in der Stadt lauter als auf dem Land?
  • 1-seitige H_A: \mu_{M(Stadt)} > \mu_{M(Land)} bzw. \mu_{M(Stadt)} - \mu_{M(Land)}>0
• Unterscheiden sich die Gesänge von Meisen in der Stadt und auf dem Land in ihrer Lautstärke?
  • 2-seitige H_A: \mu_{M(Stadt)} \neq \mu_{M(Land)} bzw. \mu_{M(Stadt)} - \mu_{M(Land)}\neq 0)

Kohlmeisen Beispiel | U-Werte

Messung

df <- data.frame(
  origin = c(rep("Stadt",6), rep("Land",5)),
  db = c(52,44,64,53,37,50, 47,29,32,52,31)
)
df$rank <- rank(df$db, 
  ties.method = "average")

stadt <- df$db[df$origin == "Stadt"]
land <- df$db[df$origin == "Land"]

Messort	Lautstärke (in dB)	Rang
Stadt	52	8.5
Stadt	44	5
Stadt	64	11
Stadt	53	10
Stadt	37	4
Stadt	50	7
Land	47	6
Land	29	1
Land	32	3
Land	52	8.5
Land	31	2

Berechnung

Rangsummen:

R_{Stadt}=8.5+5+11+10+4+7=45.5

R_{Land}=6+1+3+8.5+2=29.5

U-Werte:

U_{Stadt}=6*5+\frac{6(6+1)}{2}-45.5 = 5.5

U_{Land}=6*5+\frac{5(5+1)}{2}-20.5 = 24.5

\Rightarrow U_{min} = U_{Stadt} = 5.5

Die Wilcoxon-Verteilung

Bestimmung von U_{krit} (bei 2-seitiger Hyopothese)

dwilcox(x = 0:(6*5), m = 6, n = 5)

qwilcox(c(0.025, 0.975), m = 6, n = 5)

[1]  4 26

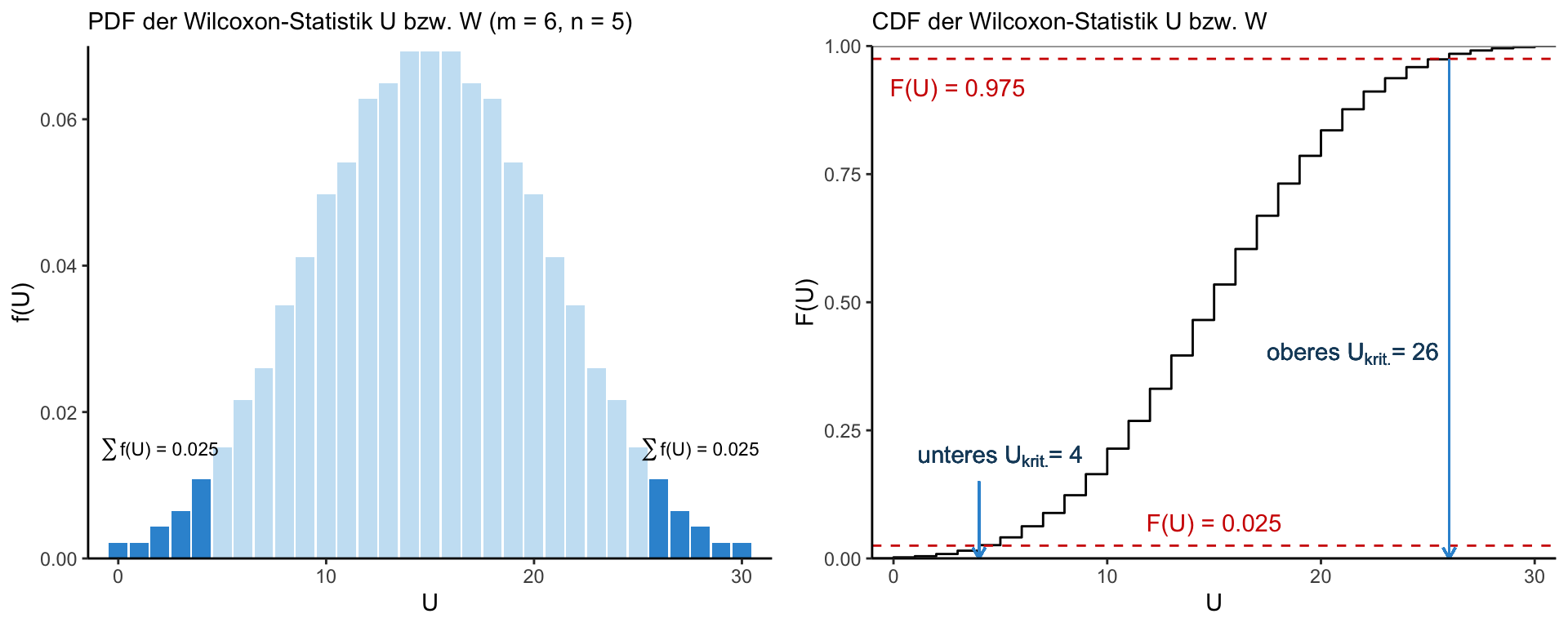
• Rangsumme der Ränge in einer Stichprobe = Zufallsvariable aus der kombinierten Rangverteilung
• Diese Rangverteilung wird Wilcoxon-Verteilung genannt und ist eine diskrete Verteilung → U_{krit} = (m, n, \alpha)
• Für große Stichproben (nicht mehr in den U-Tabellen abgebildet) wird allerdings ein Z-Wert ausgerechnet.
• Die Irrtumswahrscheinlichkeit für diesen Z-Wert kann in der Z-Tabelle nachgeschlagen bzw. in R mit pnorm() ermittelt werden.

Kohlmeisen Beispiel | Signifikanz

Manuelle Berechnung

2-seitiger Test

# krit. U
qwilcox(0.025, m = 6, n = 5)

[1] 4

# P bei U = 5.5 (mal 2!)
pwilcox(5.5, m = 6, n = 5) * 2 

[1] 0.0823

1-seitiger Test

# krit. U
qwilcox(0.05, m = 6, n = 5)

[1] 6

# P bei U = 5.5
pwilcox(5.5, m = 6, n = 5) 

[1] 0.0411

Fazit

• 2-seitiger Test:
  • U_{Stadt} < U_{\alpha = 0.025} ??
    → H_A: \mu_{M(Stadt)} \neq \mu_{M(Land)}
  • Die beiden Gruppen unterscheiden sich nicht signifikant voneinander (2-seitiger Mann-Whitney U Test, U = 5.5, p > 0.05).

• 1-seitiger Test:
  • U_{Stadt} < U_{\alpha = 0.05} ??
    → H_A: \mu_{M(Stadt)} > \mu_{M(Land)}
  • Die Lautstärke in der Stadt ist schwach signifikant höher (1-seitiger Mann-Whitney U Test, U = 5.5, p < 0.05).

Kohlmeisen Beispiel | Built-in Funktion 1

2-seitiger Test

wilcox.test(x = land, y = stadt) # Mann-Whitney U ist default

Warning in wilcox.test.default(x = land, y = stadt): cannot compute exact
p-value with ties

    Wilcoxon rank sum test with continuity correction

data:  land and stadt
W = 6, p-value = 0.1
alternative hypothesis: true location shift is not equal to 0

Warum die Warnung?

• Ein exakter p-Wert wird “standardmäßig” berechnet, wenn weniger als 50 Werte und keine gleichen Ränge (“ties”) vorhanden sind.
• Ansonsten wird eine Näherung auf Basis der Standardnormalverteilung verwendet.

Kohlmeisen Beispiel | Built-in Funktion 2

1-seitiger Test

HA: dB (Stadt) > db (Land)

wilcox.test(x = stadt, y = land, alternative = "greater")

    Wilcoxon rank sum test with continuity correction

data:  stadt and land
W = 24, p-value = 0.05
alternative hypothesis: true location shift is greater than 0

HA: dB (Land) < db (Stadt)

wilcox.test(x = land, y = stadt, alternative = "less")

    Wilcoxon rank sum test with continuity correction

data:  land and stadt
W = 6, p-value = 0.05
alternative hypothesis: true location shift is less than 0

Die Reihenfolge von x und y zählt für U (bzw. W)!

• Es wird immer der U-Wert der Stichprobe wiedergegeben, die in der Funktion dem y Argument zugewiesen wird!
• Falls dieser der größere ist, wird der obere U_{krit} verwendet.

Hier wurde die Warnung unterdrückt.

Übersicht der Funktionsanwendungen

• Unabhängiger Zweistichproben-Test: Mann-Whitney U-Test, zweiseitige Hypothese (Standard): H_A: µ1 ≠ µ2
  • wilcox.test(x, y)
• Unabhängiger Zweistichproben-Test: Mann-Whitney U-Test, einseitig: H_A: µ1 > µ2:
  • wilcox.test(x, y, alternative = “greater”)
• Gepaarter Zweistichproben-Test: Wilcoxon-Vorzeichen-Rang-Test, zweiseitige Hypothese: H_A: µ1 ≠ µ2
  • wilcox.test(x, y, paired = TRUE)
• Gepaarter Zweistichproben-Test: Wilcoxon-Vorzeichen-Rang-Test, einseitig: H_A: µ1 < µ2
  • wilcox.test(x, y, paired = TRUE, alternative = “less”)

Mann-Whitney U-Test vs. t-Test

Vergleich Mann-Whitney U-Test vs. t-Test

Einfluss von Ausreißern

Unterscheiden sich mit Fadenwürmern infizierte und mit Interleucin-33 behandelte Mäuse von nicht behandelten Kontrollen in der Zahl adulter Fadenwürmer im Dünndarm?

wurm <- data.frame(interleucin = c(5,5,5,6,8,10,10,11, 120),
                   kontrolle = c(14,17,18,20,22,24,25,26,23))

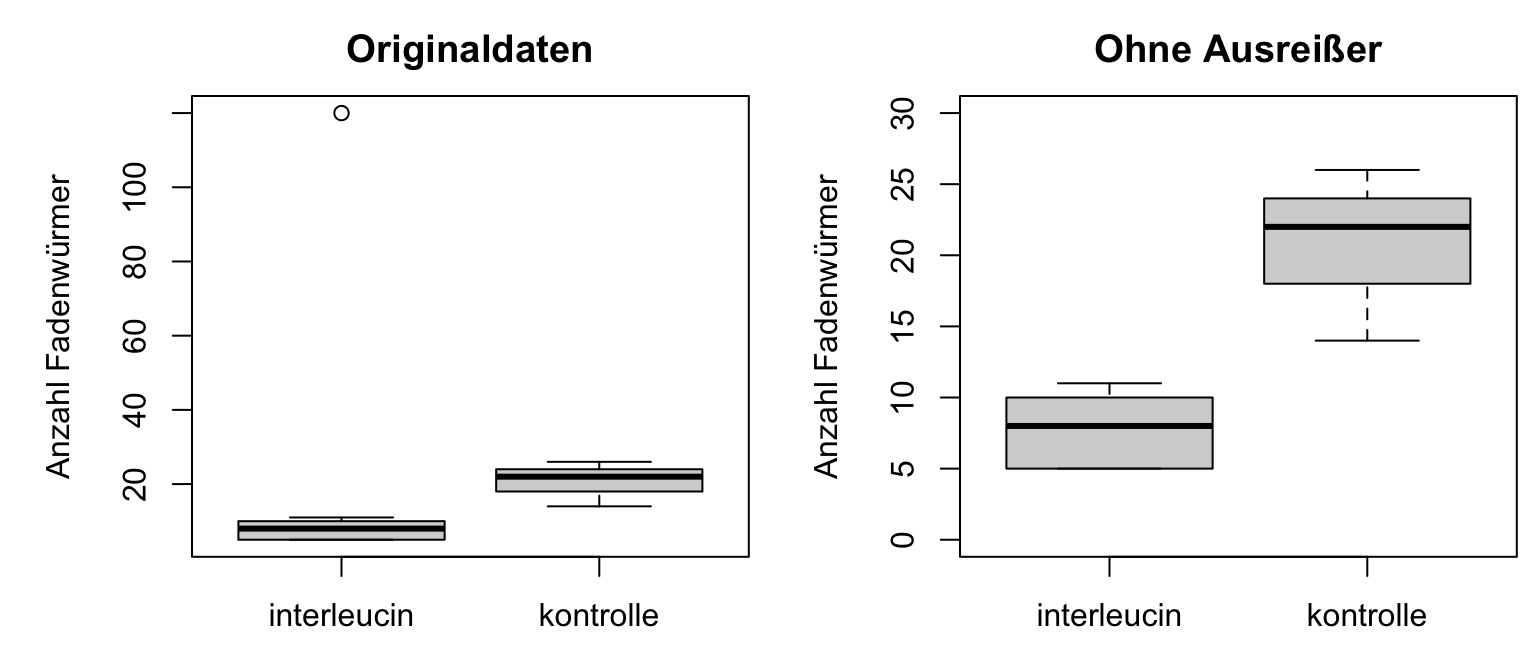
Testergebnisse mit dem Ausreißer

Mann-Whitney U-Test

wilcox.test(x = wurm$interleucin, 
  y = wurm$kontrolle)

    Wilcoxon rank sum test with continuity correction

data:  wurm$interleucin and wurm$kontrolle
W = 9, p-value = 0.006
alternative hypothesis: true location shift is not equal to 0

→ H_0 kann abgelehnt werden. Es gibt einen signifikanten Unterschied.

Welch t-Test

t.test(x = wurm$interleucin, 
  y = wurm$kontrolle, 
  var.equal = FALSE)

    Welch Two Sample t-test

data:  wurm$interleucin and wurm$kontrolle
t = -0.08, df = 8, p-value = 0.9
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -29.9  27.9
sample estimates:
mean of x mean of y 
       20        21 

→ H_0 kann nicht abgelehnt werden. Es gibt keinen signifikanten Unterschied.

Testergebnisse ohne den Ausreißer

Mann-Whitney U-Test

wilcox.test(x = wurm$interleucin[-9], 
  y = wurm$kontrolle[-9])

    Wilcoxon rank sum test with continuity correction

data:  wurm$interleucin[-9] and wurm$kontrolle[-9]
W = 0, p-value = 0.0009
alternative hypothesis: true location shift is not equal to 0

→ H_0 kann weiterhin abgelehnt werden. Es gibt einen signifikanten Unterschied.

Welch t-Test

t.test(x = wurm$interleucin[-9], 
  y = wurm$kontrolle[-9], 
  var.equal = FALSE)

    Welch Two Sample t-test

data:  wurm$interleucin[-9] and wurm$kontrolle[-9]
t = -8, df = 12, p-value = 8e-06
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -17.08  -9.42
sample estimates:
mean of x mean of y 
      7.5      20.8 

→ Jetzt kann H_0 abgelehnt werden.

Nicht-parametrische Tests sind wesentlich weniger sensitiv gegenüber Ausreißern!

Übungsaufgaben

Übungstag 3

Einführung in die inferenzielle Statistik

• Aufgaben:
  • 3.1 Hausaufgabe zur Vorbereitung:
    Erstellung von Hypothesen - Korallenriffe
  • 3.2 Klassische Tests zum Prüfen auf Unterschiede zwischen 2 Stichproben
  • 3.3 Nachbereitung Fallstudie: Frage 2.1
• R Notebook-Skript:
  • DS2_03_Uebungen_Hypothesen_Anpassungstests_Zweistichprobentests.Rmd

s. Handbuch - Abschnitt ‘Übungen’

Fragen?

Abschlussquiz

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de


Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.