
5-Hypothesentest oder was ist eine H0?
Data Science 2
Saskia Otto & Monika Eberhard
Universität Hamburg, IMF & IZS
Sommersemester 2025
Lernziele
Nach Abschluss dieser VL und Übung..
- können Sie eigene Forschungshypothesen formulieren.
- kennen Sie den Unterschied zwischen der Null- und Alternativ-Hypothese
- können Sie Hypothesentests schrittweise durchführen.
- können Sie Stichproben auf ihre Normalverteilung und Varianzhomogenität testen.
Heutige Frage
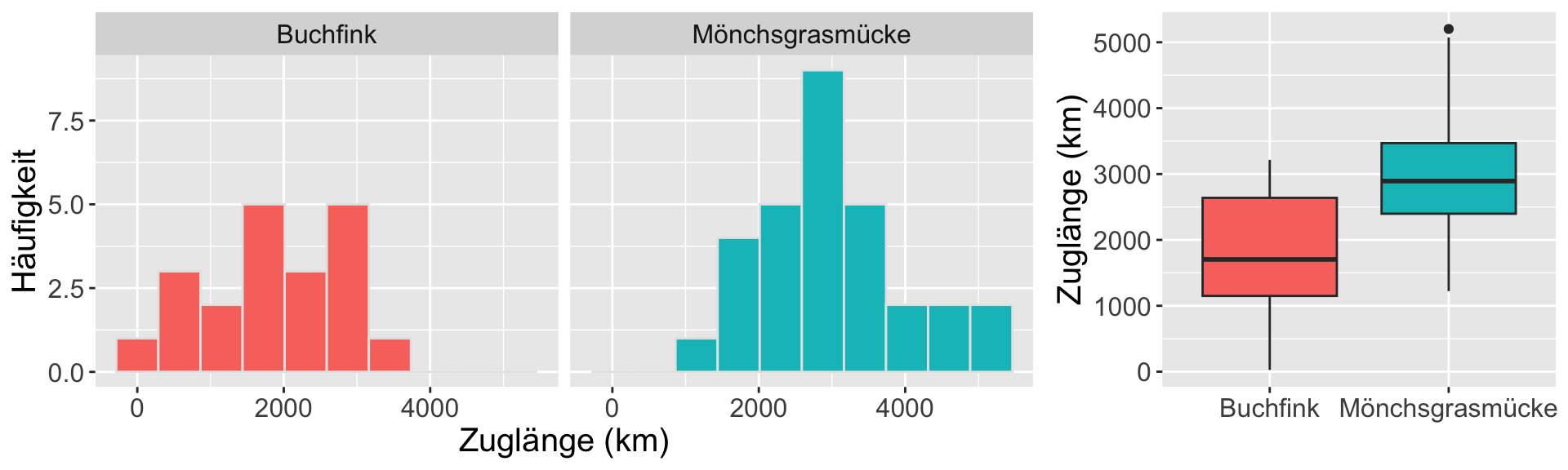
Können wir sagen dass, basierend auf unserer Stichprobe, die intraspezifische Streuung des Zugverhaltens bei Buchfinken allgemein kleiner ist als bei der Mönchsgrasmücke?


Bildquellen: Wikipedia (Buchfink unter CC BY-SA 2.5 Lizenz) und Mönchsgrasmücke unter CC0 Lizenz)
Klassischer Weg in der inferenziellen Statistik | 1
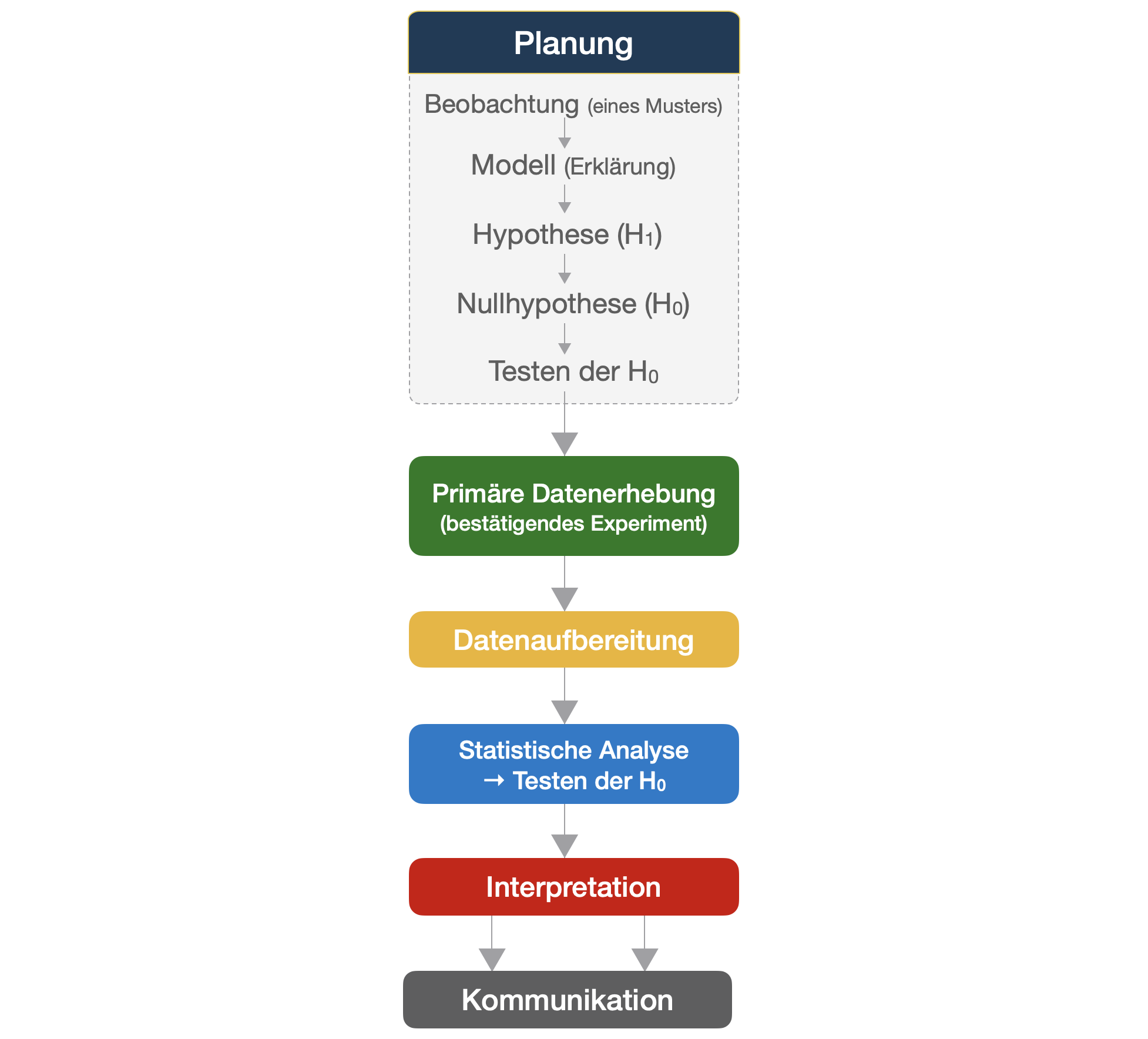
Klassischer Weg in der inferenziellen Statistik | 2
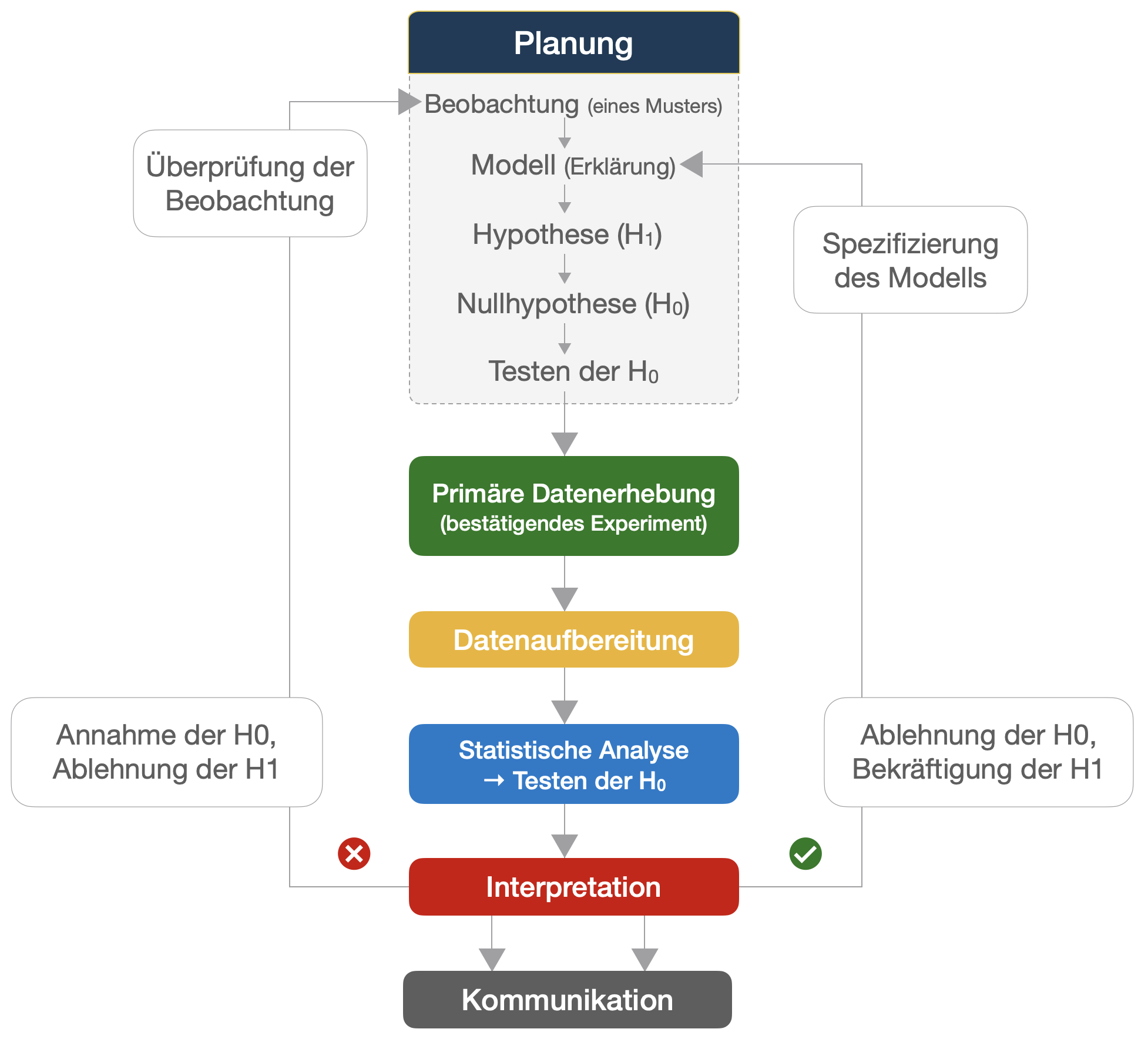
Formulierung der Hypothesen

Was ist ein MUSTER?
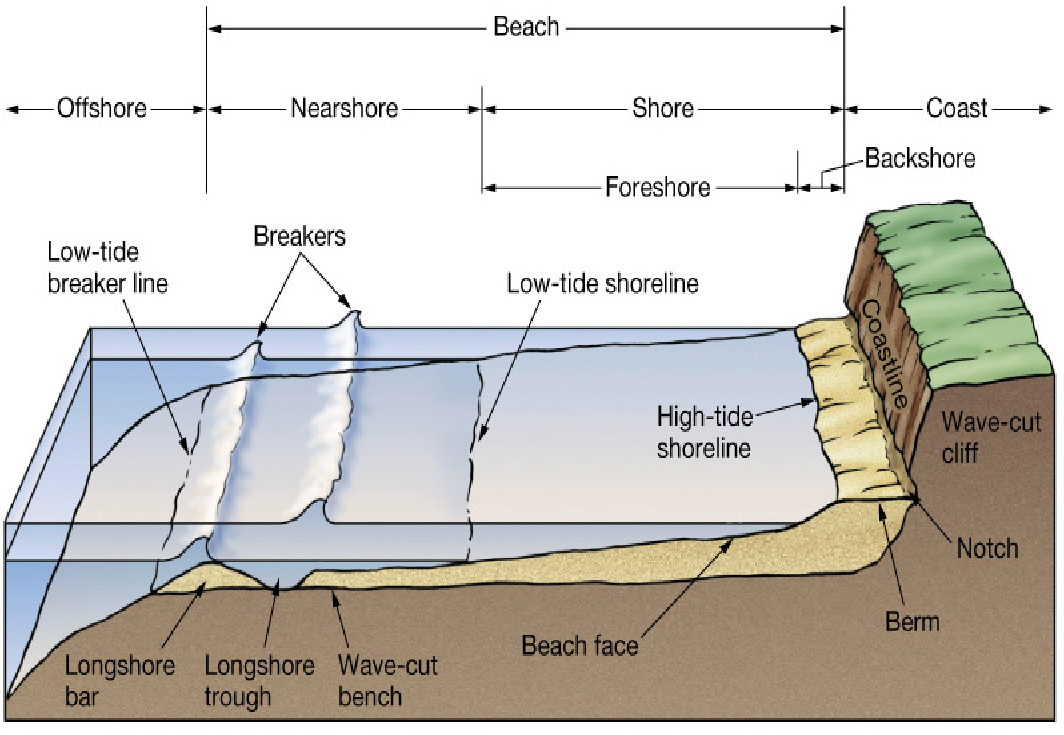

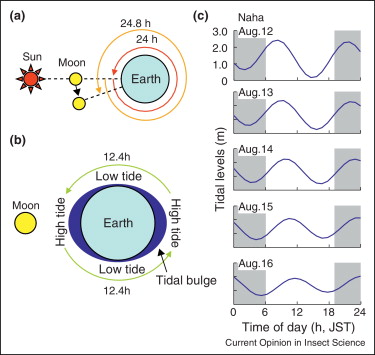
- Kein Chaos oder stochastisches Verhalten
- Regelmäßigkeiten, z.B.
- Räumliche Verteilungen (Küstenzonierung, Umweltgradienten, Streifenmuster bei Schlangen)
- Zeitliche Rhythmen (Sonnenaufgang, Mondphasen, Jahreszeiten, Gezeiten)
- Stetige Veränderungen (Alterung, Wachstum, Klimawandel)
![]() Das MODELL ist eine Erklärung für das Muster, es postuliert Regeln oder Prozesse.
Das MODELL ist eine Erklärung für das Muster, es postuliert Regeln oder Prozesse.
Bildquellen: Goto & Takekata 2015, H.Y. Siry 2007
MUSTER: Saisonale Wanderung einer Fischpopulation
4 mögliche Modelle
- Modell 1: Die Fische folgen der Beute.
- Modell 2: Die Fische meiden saisonal auftauchende Raubtiere.
- Modell 3: Die Fische meiden saisonal niedrige Temperaturen.
- Modell 4: Es ist Gottes Wille.
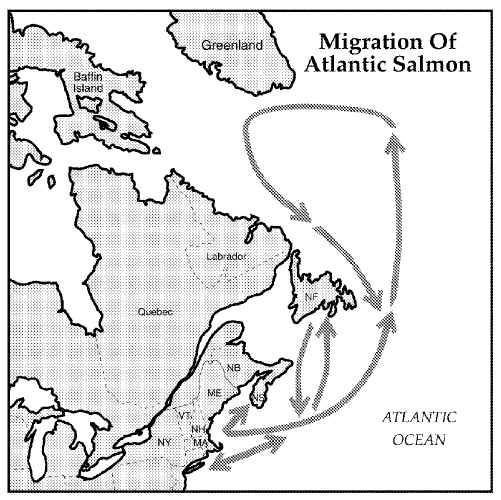
Abb. rechts: Meereswanderung des Atlantischen Lachses
(Atlantic Salmon Life Cycle, U.S. Fish & Wildlife Service, 2010)
Hypothesen
- sollten kurz und prägnant, spezifisch zum Modell und testbar sein:
- H1:
‘Die marine Biodiversität auf den Philippinen ist die größte im Universium.’ - H1: ‘Die marine Biodiversität auf den Philippinen ist die größte in Südostasien.’
- H1:
- beziehen sich direkt auf das durchzuführende Experiment.
- Sprich, sie können als aus dem Modell abgeleitete Vorhersage formuliert werden.
HYPOTHESEN: Saisonale Wanderung einer Fischpopulation
4 mögliche Modelle
- Modell 1: Die Fische folgen der Beute.
- H1: Wenn die Fische gefüttert werden, bleiben sie.
- Modell 2: Die Fische meiden saisonal auftauchende Raubtiere.
- H1: Wenn die Raubtiere reduziert oder aus dem Gebiet ausgeschlossen werden,…
- Modell 3: Die Fische meiden saisonal niedrige Temperature.
- H1: Wenn der Kühlwasserabfluss erhöht wird, …
- Modell 4: Es ist Gottes Wille.
- H1: ???

Hypothesen können..
- richtungsunabhängig sein:
- Änderungen des Fischereidrucks werden die Fischbestände verändern.
- richtungsabhängig sein:
- Eine Zunahme des Fischereidrucks wird die Fischbestände verringern.
- richtungsabhängig sein und eine Größenordnung enthalten:
- Eine Erhöhung des Fischereidrucks um 10% wird die Fischbestände um 50% reduzieren.
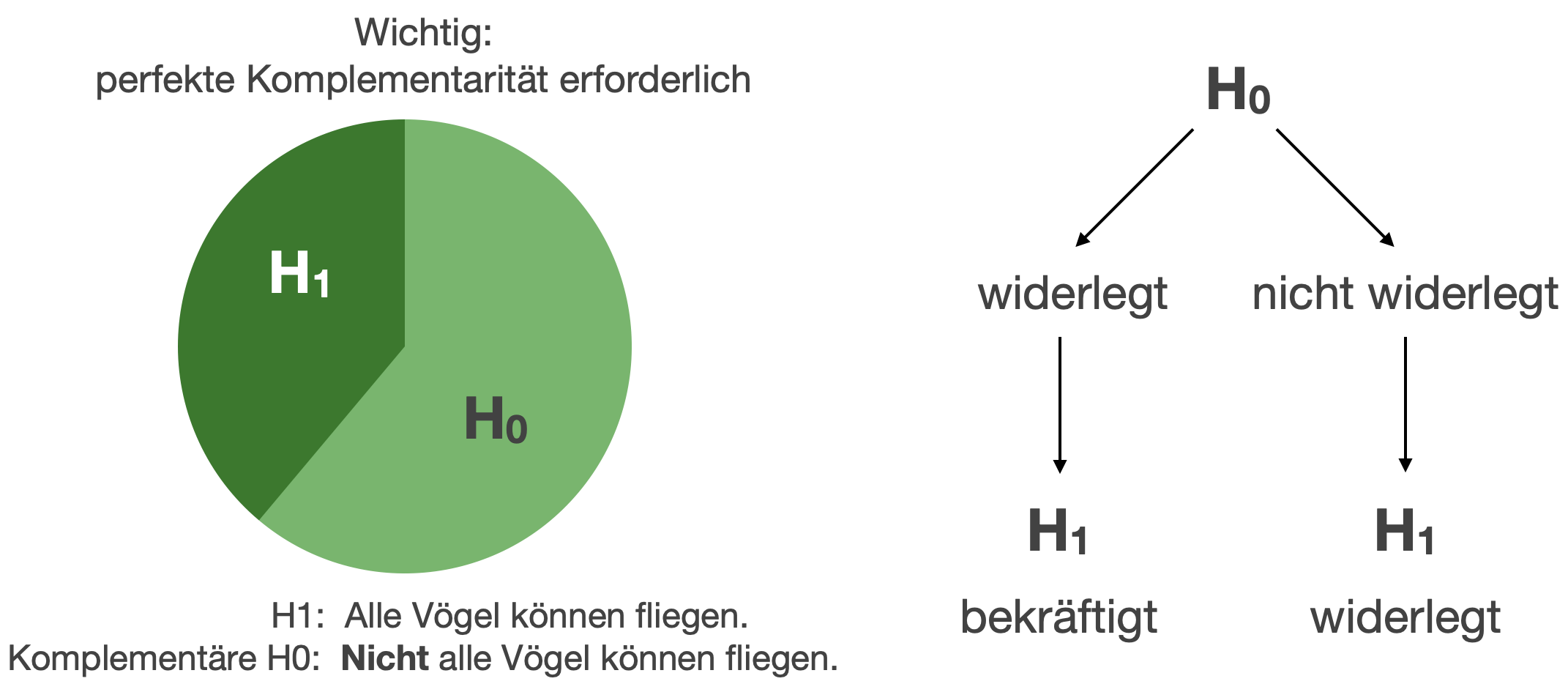
Sir Karl Poppers Idee der Widerlegung oder Falsifikation
- Der Wahrheitsgehalt einer Vorhersage kann nicht für alle Fälle, Orte und Zeiten bewiesen werden, aber ihre Widerlegung ist leicht möglich!
- → Bestärkung der H1 durch Widerlegung der Gegenhypothese (sog. Null-Hypothese oder H0).
Unspezifische Hypothese | 1
Wenn die Hypothese nicht spezifisch zum Modell ist:
- Beobachtung: Geringe Anzahlen der Art A treten mit großen Anzahlen von Art B auf und umgekehrt.
- Modell: Art A und B sind Konkurrenten.
- H1: Wenn ich A entferne, wird B in seiner Häufigkeit zunehmen.
- H0: Wenn ich A entferne, wird B in seiner Anzahl gleich bleiben oder sogar abnehmen.
→ Wenn H0 abgelehnt wird, akzeptieren wir unsere (Alternativ-) Hypothese H1 und damit unser Modell.
Unspezifische Hypothese | 2
Problem:
- Andere Modelle können zur gleichen Hypothese führen.
- Das wahre Modell könnte sein:
- A trägt eine Krankheit in sich, die B tötet → also gibt es keine Konkurrenz um die begrenzten Ressourcen.
- Das Modell ist recht spezifisch (es postuliert den Mechanismus der Konkurrenz), während H1 allgemeiner ist.
Hypothesen bei Mittelwertsvergleichen
Zweiseitige Hypothese
- H_A: \mu_1 \neq \mu_2
- H_0: \mu_1 = \mu_2
Beispiel:
Die Gesänge von Meisen in der Stadt und auf dem Land unterscheiden sich in ihrer durchschnittlichen Lautstärke.
Einseitige Hypothese
- H_A: \mu_1 > \mu_2 bzw. \mu_1 < \mu_2
- H_0: \mu_1 \leq \mu_2 bzw. \mu_1 \geq \mu_2
Beispiel:
Kohlmeisen in der Stadt singen durchschnittlich lauter als auf dem Land.
Wichtig!
Die Alternativhypothese muss immer eine Effektgröße enthalten.
‘Es gibt keinen Unterschied’ kann daher keine H_A sein!
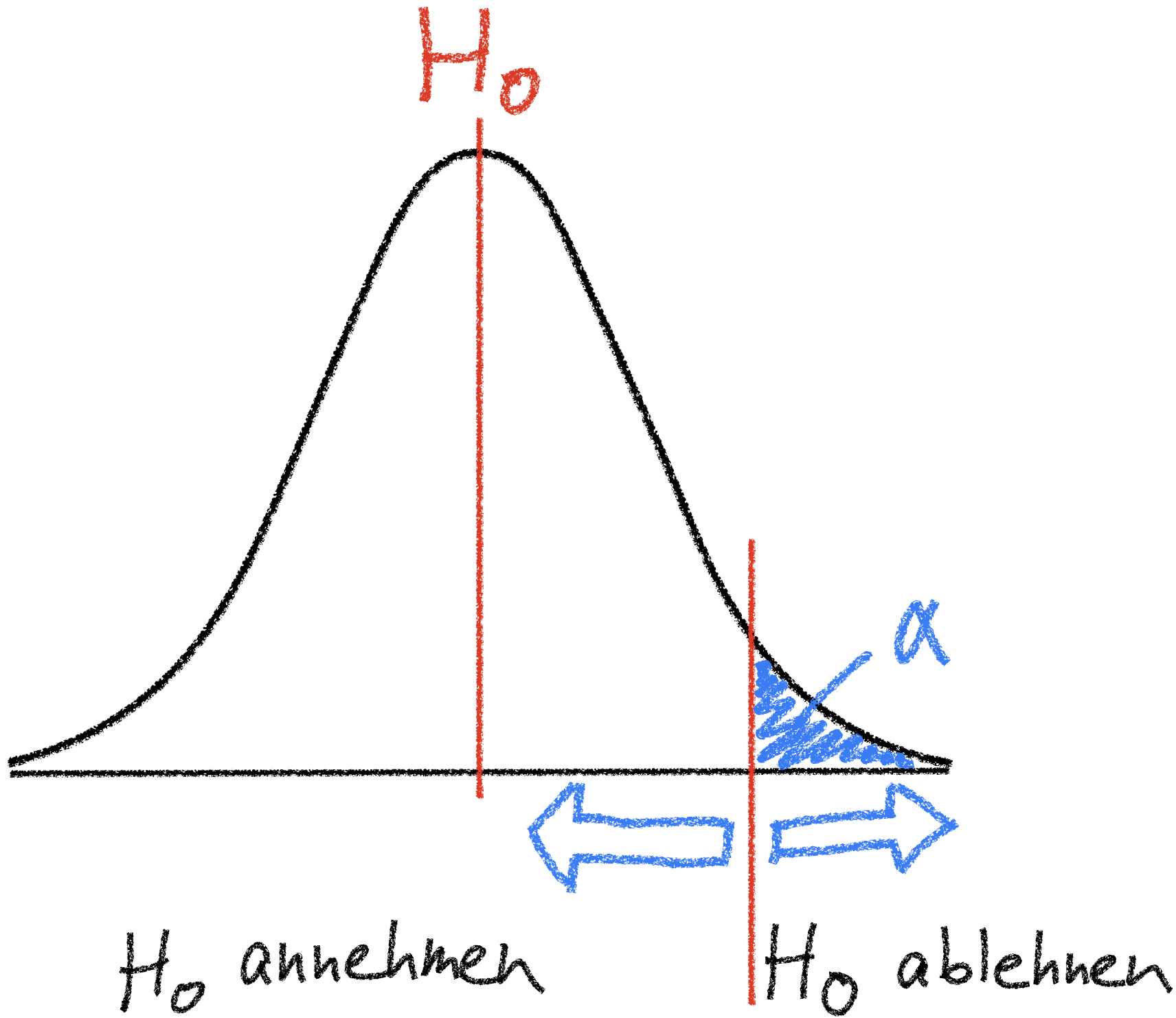
Signifikanztests

Was sind Signifikanztests?
- Zielen auf eine Entscheidung über die Beibehaltung oder Ablehnung einer statistischen Hypothese ab.
- Die Hypothese bezieht sich immer auf einen statistischen Kennwert.
- Je nachdem, ob der Stichprobenkennwert in den Annahme- oder Ablehnungsbereich fällt (also größer oder kleiner als der kritischen Werte ist), wird die Hypothese als richtig oder nicht zutreffend angesehen.
Vorgehensweise
8 Schritte - ausgehend von einer Forschungshypothese
- Wahl der Statistik, welcher die Daten bezogen auf die Forschungshypothese beschreibt (z.B. Mittelwert oder Varianz).
- Formulierung der Nullhypothese H_0 und der (logisch) entgegengesetzten Alternativhypothese H_A bzw. H_1 → einseitig, gerichtet oder zweiseitig, ungerichtet
- Erhebung empirischer Daten und Überprüfung der Stichprobenverteilung.
- Finale Wahl des statistischen Test und Berechnung der entsprechenden Teststatistik.
- Festlegung der Irrtumswahrscheinlichkeit (Signifikanzniveau \alpha) → üblicherweise 5%.
- Festlegung des Annahme- und Ablehnungsbereich mit dem kritischen Wert aus der Prüfverteilung (in Abhängigkeit vom Signifikanzniveau und den Freiheitsgraden).
- Entscheidung H_0 beizubehalten oder abzulehnen.
- Zusammenfassung des Testergebnis bezogen auf die eigentliche Forschungshypothese.
Schritt 1 | Wahl der Statistik
Beispiel einer Forschungshypothese
Die intraspezifische Streuung des Zugverhaltens ist bei Buchfinken kleiner als bei der Mönchsgrasmücke.


Zu vergleichender Parameter bzw. Kennwert
Die Varianz \sigma^2 bzw. s^2
Bildquellen: Wikipedia (Buchfink unter CC BY-SA 2.5 Lizenz) und Mönchsgrasmücke unter CC0 Lizenz)
Schritt 2 | Formulierung der Hypothesen
Beispiel Zugverhalten
Die intraspezifische Streuung des Zugverhaltens ist bei Buchfinken kleiner als bei der Mönchsgrasmücke.


Hypothesen (einseitig)
- H_A: \sigma_{Buchfink}^2 < \sigma_{Mönchsgrasmücke}^2
- H_0: \sigma_{Buchfink}^2 \geq \sigma_{Mönchsgrasmücke}^2
Bildquellen: Wikipedia (Buchfink unter CC BY-SA 2.5 Lizenz) und Mönchsgrasmücke unter CC0 Lizenz)
Schritt 3 | Datenerhebung und -exploration
Beispiel Zugverhalten
| Kenngröße | Buchfink | Mönchsgrasmücke |
|---|---|---|
| Mittelwert x̅ | 1800 km | 3000 km |
| Standardabweichung s | ±900 km | ±1000 km |
| Stichprobengröße n | 20 | 30 |


Wahl des statistischen Test | Schritt 4
Folgende grundlegende Fragen müssen beantwortet werden:
- Welches Skalenniveau liegt vor (nominal, ordinal, metrisch)?
- Wie viele Stichproben sollen verglichen werden (1, 2, ≥2)?
- Was soll getestet werden (Abweichungen von einer Verteilung, einer erwarteten Häufigkeitsverteilung, einem Erwartungswert)?
- Ermöglicht die Stichprobenverteilung die Anwendung parametrischer Verfahren, d.h. sind die Daten normal verteilt (und Varianzhomogen) (Schritt 3)?
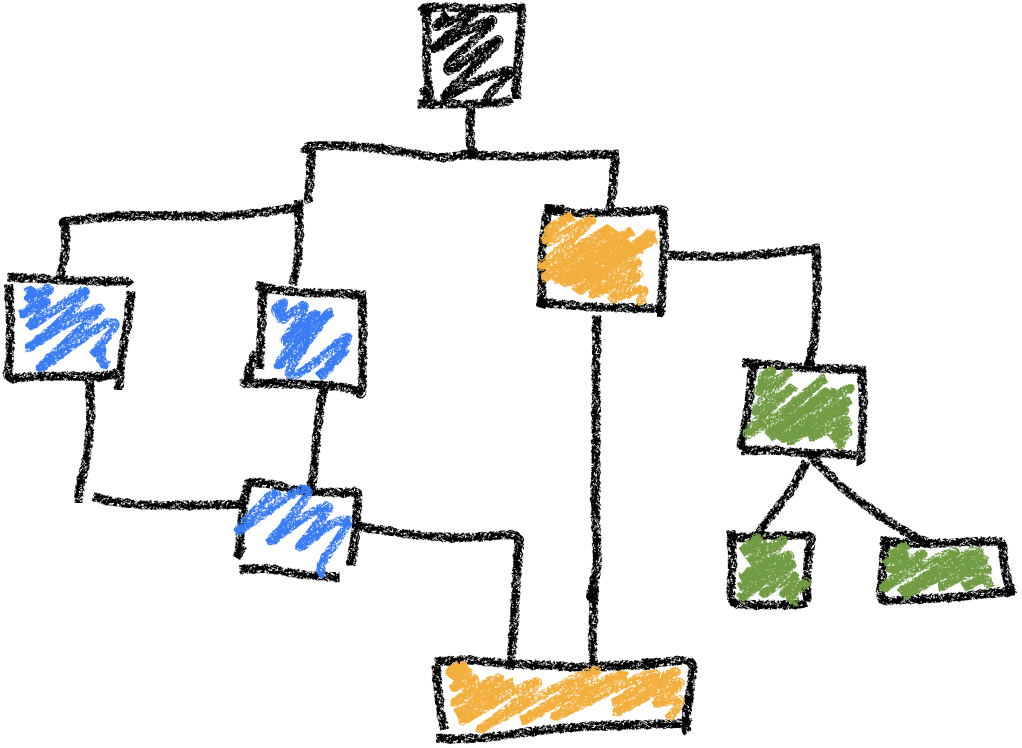
Wahl des statistischen Test | Übersicht
Klassische Tests
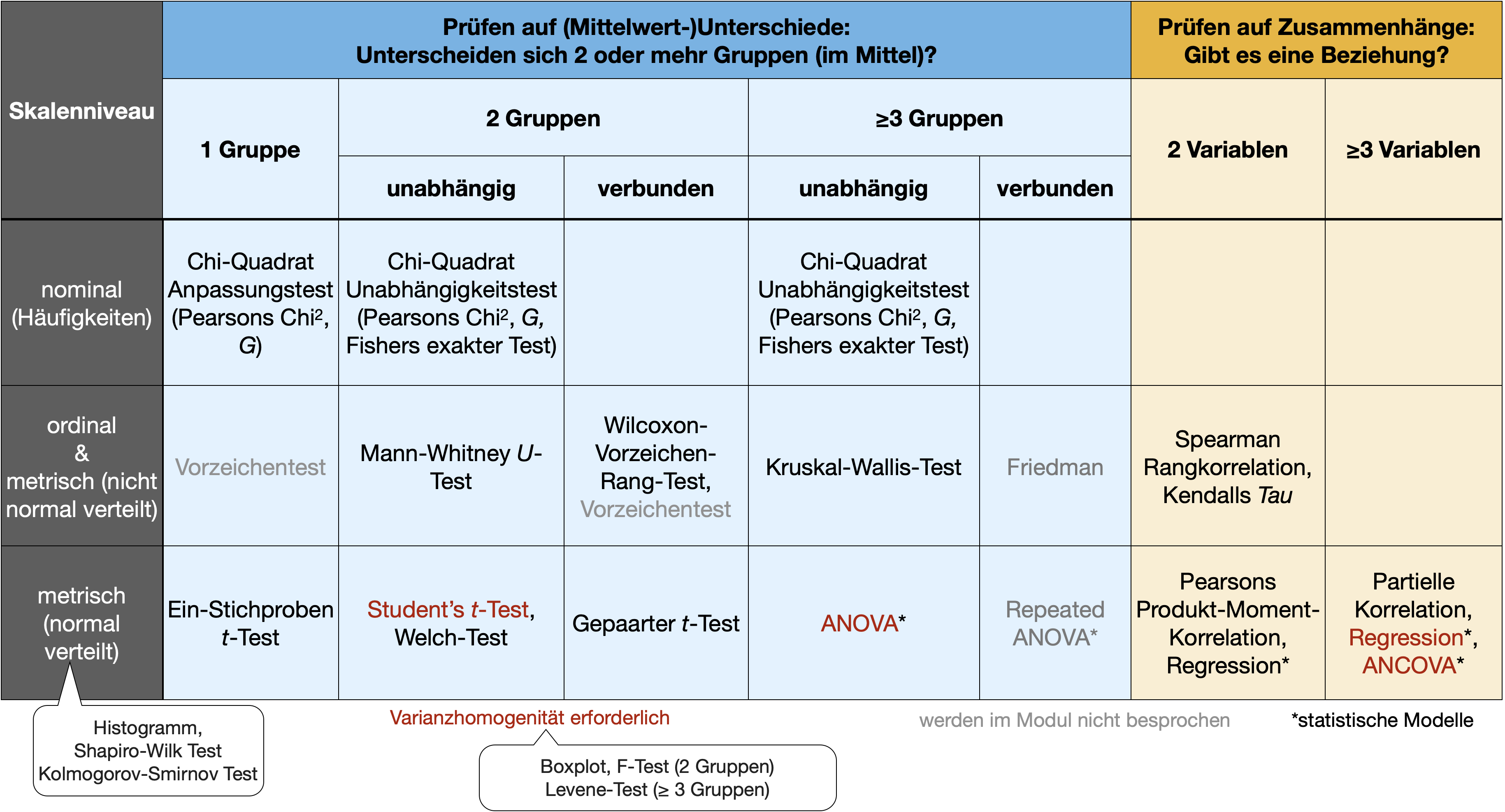
Wahl des statistischen Test | Entscheidungsbaum
Entscheidungsbaum (auch im Handbuch enthalten) sollte für die Fallstudie verwendet werden.
Signifikanzniveau | Schritt 5
oder auch Irrtumswahrscheinlichkeit \alpha
- Wahrscheinlichkeit für die Ablehnung der H_0, obwohl diese zutrifft (’bedingte Wahrscheinlichkeit, Fehler 1. Art).
- In der Statistik ist ein Ergebnis dann signifikant, wenn es unwahrscheinlich ist, dass es zufällig aufgetreten ist, vorausgesetzt, eine angenommene H_0 ist wahr.
- Wenn das beobachtete Signifikanzniveau klein genug ist, wird die H_0 verworfen.
Übliche Signifikanzwerte
- Signifikant: p ≤ 0.05
- Hoch signifikant: p ≤ 0.01
- Höchst signifikant: p ≤ 0.001
- Schwach signifikant: 0.05 ≤ p < 0.01
- Schwach nicht signifikant: 0.1 ≤ p < 0.05
Statistische Fehler 1. und 2. Art
Fehler 1. Art (\alpha)
- H_A wird angenommen obwohl H_0 richtig ist, d.h. H_0 wird fälschlicherweise verworfen obwohl nur zufällige Unterschiede vorhanden sind.
- Das sog. Risiko 1. Art is somit gleich der Irrtumswahrscheinlichkeit
Fehler 2. Art (\beta)
- Es werden keine signifikanten Unterschiede erkannt, obwohl die H_0 falsch ist, d.h. die Unterschiede werden als zufällig interpretiert.
- Bei vorgegebenen n wird \beta umso größer, je kleiner \alpha festgelegt wird.
| Entscheidung | H_0 trifft zu | H_0 trifft nicht zu |
|---|---|---|
| H_0 wird nicht abgelehnt | Richtige Entscheidung; kein Effekt nachgewiesen | \beta-Fehler; vorhandenen Effekt nicht nachgewiesen |
| H_0 wird abgelehnt | \alpha-Fehler; Effekt nachgewiesen, den es nicht gibt | Richtige Entscheidung; vorhandenen Effekt nachgewiesen |
Berechnung von β
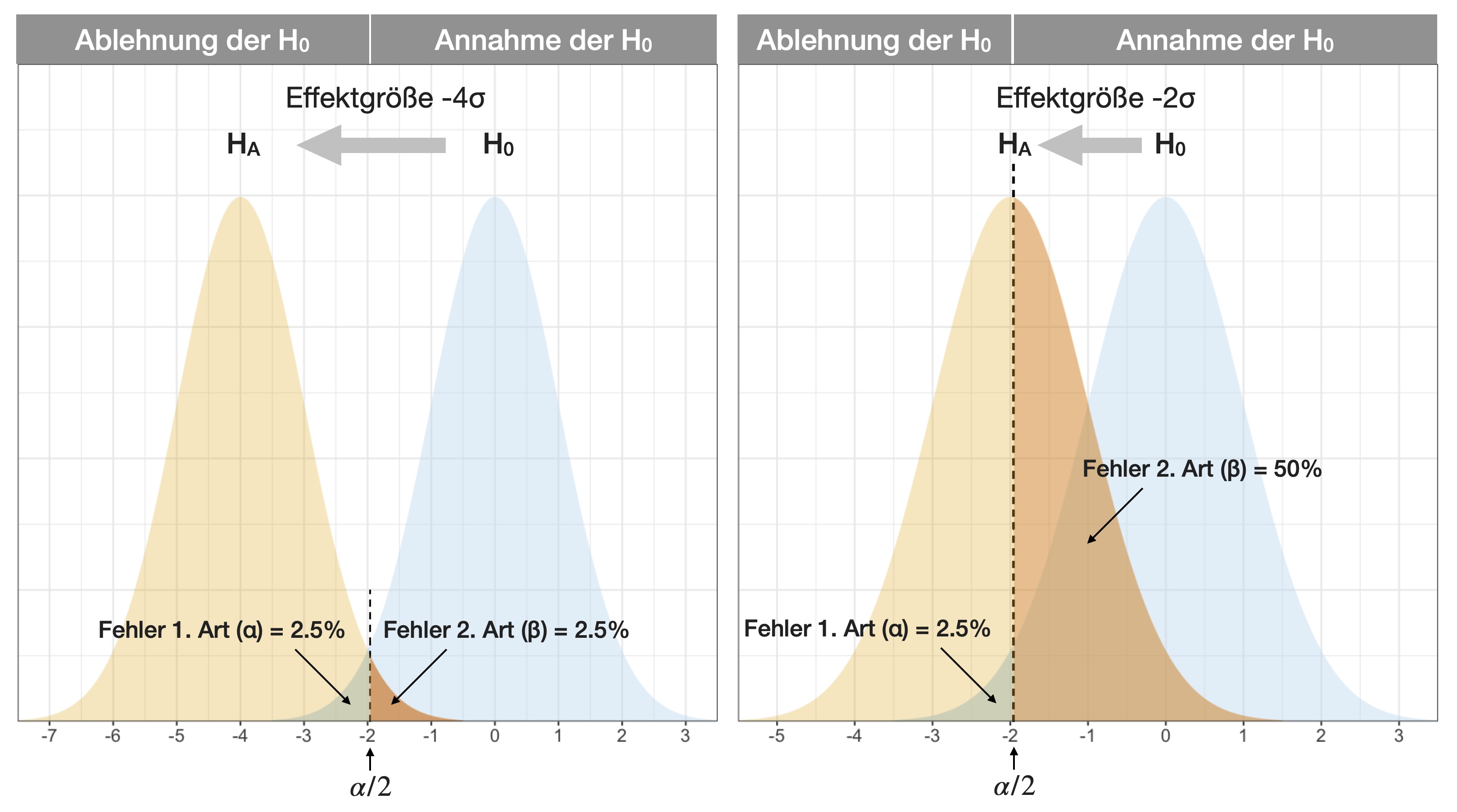
Fall 1 (links): Angenommen, wir testen die H_A, dass der Durchschnitt unserer Probe -4σ Einheiten von der H_0 entfernt sei und die H_A ist wahr. Dann ist für eine Zufallsprobe aus dieser Population die Wahrscheinlichkeit, dass sie in den Akzeptanzbereich von H_0 fällt (welcher bei ±1.96σ um μ liegt wenn α = 0.05), etwa 2.5% → β = 0.025 und die Teststärke ist dann 1-0.025=0.975 (im Durchschnitt würden wir für 97.5% aller Proben die H_0 korrekt verwerfen).
Fall 2 (rechts): Angenommen, der Unterschied der H_0 und H_A Population liegt nur noch bei -2σ Einheiten. Dann ist die Wahrscheinlichkeit, dass eine zufällig gewählte Probe von H_A außerhalb des kritischen Bereichs fällt (μ ± 1.96σ) nur noch 50%. Bei der Hälfte aller Proben würden wir also die H_0 fälschlicherweise akzeptieren (Fehler 2. Art).
Einflussgrößen von β
- Differenz zwischen H_0 und H_A (engl.: effect size) → je größer die Differenz, desto kleiner wird die \beta-Wahrscheinlichkeit.
- Wahl des Signifikanzniveaus → je kleiner \alpha desto größer wird \beta, da sich die Verwerfungsregion weiter von H_0 entfernt.
- Genauigkeit des geschätzten Parameters → abhängig von Stichprobengröße
- Beziehung zwischen \alpha, \beta, Effekt- und Probengrößen relativ komplex.
- Zielorientierte Versuchsplanung wichtig!
- Zum Beispiel kann mittels Effektgröße, Teststärke, und den festgelegten \alpha und \beta Werten auch der Stichprobenumfang ermittelt werden. Dazu aber später mehr.
- Konsequenzen Fehler 1. und 2. Art durchdenken → Was ist vorzuziehen?
Wann wird welcher Fehler vorgezogen?
Medizinische oder pharmazeutische Studien
Hier würden viele lieber einen Fehler 2. Art als einen Fehler 1. Art begehen:
- Die Ablehnung einer wahren H_0 führt dazu, dass wir unsere Alternativhypothese akzeptieren.
- Die Beibehaltung der H_0 führt dazu, dass wir bei neuen Versuchen wieder zu unseren Beobachtungen zurückkehren und weiter forschen → es wurde nichts verworfen.
Umweltstudien
Hier wäre es als Vorsichtsmaßnahme besser, einen Fehler 1. Art zu machen:
- Die Annahme, dass es keine Effekte gibt, wenn es tatsächlich welche gibt (\beta-Fehler), ist viel gefährlicher als die Konsequenz der Annahme, dass es Effekte gibt (und entsprechende Maßnahmen ergriffen werden müssen), wenn es wirklich keine Effekte gibt (\alpha-Fehler).
Interpretation von p-Werten
Was denken einige Statistiker über Signifikanz?
It is very bad practice to summarize an important investigation solely by a value of P.
Blind adherence to the 0.05 level denies any consideration of alternative strategies, and it is a serious impediment to the interpretation of data ( e.g. 0.049 is significant, but 0.051 is not significant).
Scientist care about whether a result is statistically significant, but they should care much more about whether it is meaningful.
Festlegung des Ablehnungsbereichs | Schritt 6
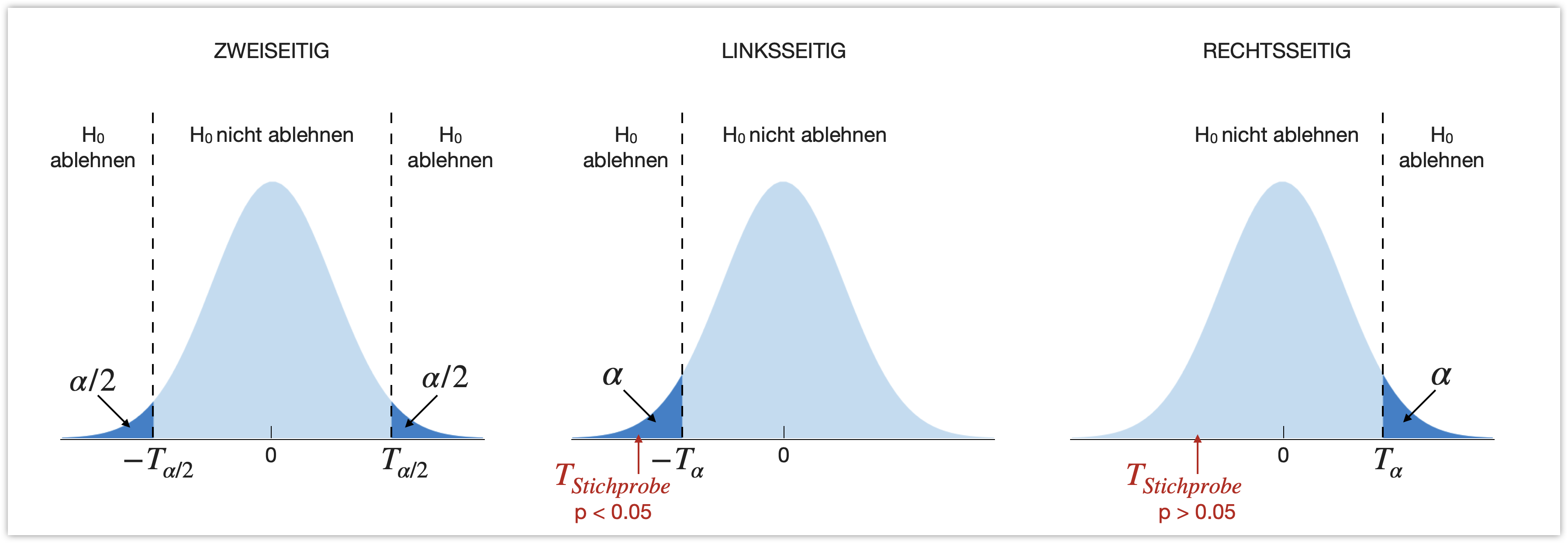
Der statistische Test..
liefert eine Teststatistik (T) und eine Wahrscheinlichkeit (p-Wert) basierend auf dessen Prüfverteilung, dass das statistische Ergebnis so extrem ausfällt wie das beobachtete, wenn die Nullhypothese wahr wäre (nach der z.B. zwei Stichproben zur gleichen Grundgesamtheit gehören).
Zusammenfassung | Schritt 8
Bei den klassischen Tests sollte immer die Teststatistik, der bzw. die Freiheitsgrade (für die Prüfverteilung), und der p-Wert angegeben werden:

Testauswahl

Auswahl des richtigen Test

Zwei große Gruppen von klassischen Tests
Parametrische Tests
- Verteilungsabhängig
- Arbeiten mit \bar{X}, s^2, s
- Nur für metrische Daten
- Annahmen:
- Unabhängigkeit (außer gepaarter t-Test)
- Varianzhomogenität (gleiche Varianzen)
- Normalität (Normalverteilung)
- Tests:
- F-Test,
- t-Test für 1 und 2 Stichproben
- Varianzanalyse (ANOVA), Kovarianzanalyse (ANCOVA)
- Pearson Produkt-Moment-Korrelationskoeffizient, lineare Regression
Nicht-Parametrische Tests
- Verteilungsfrei (keine Normalverteilung erforderlich)
- Arbeiten mit Median und Rängen
- Für metrische, ordinale, und nominale Daten
- Teststärke ist allgemein niedriger
- Nicht geeignet, wenn das Design komplex ist
- Tests:
- Mann-Whitney U-Test
- Wilcoxon-Vorzeichen-Rang-Test
- Chi-Quadrat-Tests
- Kruskal-Wallis-Test, Friedman-Test
- Rangkorrelation (z.B. Spearman, Kendall)
Überprüfung der Testannahmen bei metrischen Daten

Auf Normalverteilung testen (Anpassungstest)
- Shapiro-Wilk-Test -
shapiro.test():- Vorteil: Gute Teststärke über einen weiten Bereich von Nicht-Normalverteilungstypen und Stichprobengrößen (daher bei N < 50 vorzuziehen).
- Nachteil: Weniger robust wenn Autokorrelation auftritt.
- Kolmogorov-Smirnov-Test -
ks.test():- Vorteil: Verteilungsfrei, d.h. es kann auf verschiedenste theoretische Verteilungen getestet werden. Im Falle von Autokorrelation robuster als S-W-Test.
- Nachteil: Geringere Teststärke (die H_0 wird seltener korrekt abgelehnt).
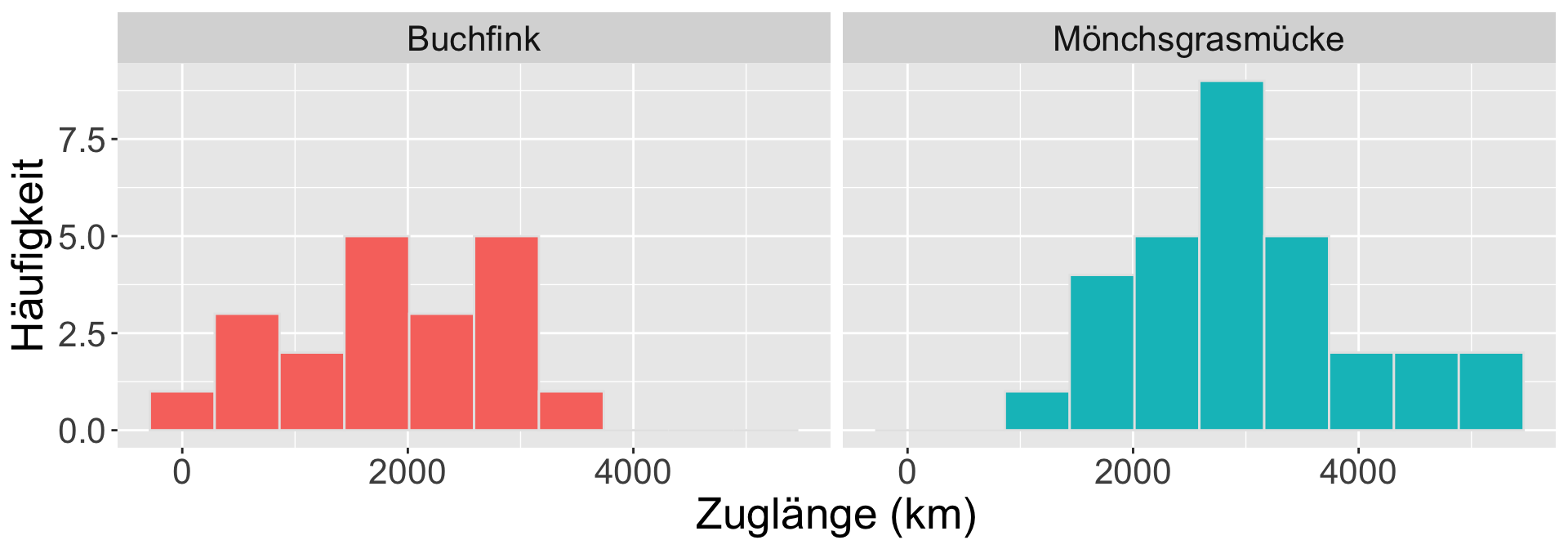
Normalität: Shapiro-Wilk-Test
Beispiel Zugverhalten
| Kennwert: | \mu, \sigma^2 bzw. \bar{X} und s^2 |
| H0: | X ist normalverteilt |
| HA: | X ist nicht normalverteilt |
| Teststatistik: | W |
| alpha: | 5% |
| p-Wert: | Vergleich Teststatistik W mit kritischen Wert für den Ablehnungsbereich (aus Verteilung der Teststatistik) |
Shapiro-Wilk normality test
data: bf
W = 1, p-value = 0.5
Shapiro-Wilk normality test
data: mgm
W = 1, p-value = 0.6- H_0 kann in beiden Tests nicht abgelehnt werden, da die p-Werte > 0.05 sind.
- → beide Stichproben sind normalverteilt (W = 0.96, p = 0.5 bzw. W = 0.97, p = 0.6).
Normalität: Kolmogorov-Smirnov-Test
Beispiel Zugverhalten
Built-in Funktion ks.test()
Exact one-sample Kolmogorov-Smirnov test
data: bf
D = 0.1, p-value = 0.9
alternative hypothesis: two-sided
Exact one-sample Kolmogorov-Smirnov test
data: mgm
D = 0.09, p-value = 0.9
alternative hypothesis: two-sidedAuch hier gilt:
- H_0 kann in beiden Tests nicht abgelehnt werden, da die p-Werte > 0.05 sind.
- → beide Stichproben sind normalverteilt (D = 0.12 bzw. D = 0.09, p > 0.5).
Zurück zu unserer Forschungshypothese..
Die intraspezifische Streuung des Zugverhaltens ist bei Buchfinken kleiner als bei der Mönchsgrasmücke.


Bildquellen: Wikipedia (Buchfink unter CC BY-SA 2.5 Lizenz) und Mönchsgrasmücke unter CC0 Lizenz)
Geeigneter Test zum Vergleich von Varianzen | 1
F-Test
| Kennwert: | \sigma^2 bzw. s^2 |
| H0: | \sigma^2_{BF} = \sigma^2_{MGM} bzw. F=1 |
| HA: | \sigma^2_{BF} \neq \sigma^2_{MGM} bzw. F \neq 1 |
| Voraussetzung: | Erfüllt (Daten sind normal verteilt) |
| Teststatistik: | F = \frac{\text{größeres}~s_1^2}{\text{kleineres}~s_2^2}* |
| alpha: | 5% |
| FG: | FG1 = n1-1; FG2 = n2-1 |
| p-Wert: | Der F-Wert wird mit dem F_{krit} aus der F-Verteilung verglichen. |
*Die größere Varianz kommt in den Zähler. Damit ist F immer ≥ 1.
Manuelle Berechnung in R
[1] 1.23[1] 2.08[1] 0.641- H_0 kann nicht abgelehnt werden, da p > 0.05.
Geeigneter Test zum Vergleich von Varianzen | 2
Automatische Berechnung mit der Built-in Funktion var.test()
F test to compare two variances
data: mgm and bf
F = 1, num df = 29, denom df = 19, p-value = 0.6
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.514 2.755
sample estimates:
ratio of variances
1.23 - Die intraspezifische Streuung des Zugverhaltens bei Buchfinken unterscheidet sich nicht signifikant von der bei Mönchsgrasmücken (F_{(29;19)} = 1.23, p = 0.64).
Your turn …
![]()
03:00
Quiz 1 zum Nachmachen
![]()
Normalverteilung der Kelchblattlänge
Shapiro-Wilk normality test
data: iris$Sepal.Length[iris$Species == "setosa"]
W = 1, p-value = 0.5
Shapiro-Wilk normality test
data: iris$Sepal.Length[iris$Species == "versicolor"]
W = 1, p-value = 0.5
Shapiro-Wilk normality test
data: iris$Sepal.Length[iris$Species == "virginica"]
W = 1, p-value = 0.3Quiz 2 zum Nachmachen
![]()
Varianzvergleich der Kelchblattlänge
set <- iris$Sepal.Length[iris$Species=="setosa"]
ver <- iris$Sepal.Length[iris$Species=="versicolor"]
var.test(set, ver)
F test to compare two variances
data: set and ver
F = 0.5, num df = 49, denom df = 49, p-value = 0.009
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.265 0.822
sample estimates:
ratio of variances
0.466 Übungsaufgaben
![]()
Vorbereitungsaufgabe für Übungstag 3

Was ist zu tun?
Die passenden Null- und Alternativhypothesen für ein Modell zu Veränderungen in Korallenriffen definieren.
Wichtig
Moodle-Quiz VOR der nächsten Übung ausfüllen!
Fragen?
Abschlussquiz
![]()

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de

Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.
Kurswebseite: Data Science 2