4-Schätzverfahren oder was ist ein KI?

Data Science 2

Saskia Otto & Monika Eberhard

Universität Hamburg, IMF & IZS

Sommersemester 2025

Lernziele

Nach Abschluss dieser VL und Übung werden Sie..

• den Unterschied zwischen einem Punktschätzer und einem Intervallschätzer kennen.
• wissen, wie Sie Ihre Punktschätzung optimieren können.
• verstanden haben, was es mit den Freiheitsgraden bei der Varianz auf sich hat.
• das Konfidenzintervall für den Mittelwert für große wie kleine Stichproben berechnen können.
• den Mindeststichprobenumfang für die Ermittlung eines KI für den Mittelwert berechnen können.

Heutige Frage

Unterscheiden sich verschiedene Vogelarten in Skandinavien in der mittleren Entfernung ihrer Zugdistanzen?

Buchfink

Grünfink

Mönchsgrasmücke

Bildquellen: Wikipedia (Buchfink und Grünfink unter CC BY-SA 2.5 Lizenz), Mönchsgrasmücke unter CC0 Lizenz)

Schätzverfahren

Von der Stichprobe zur Grundgesamtheit | 1

• In der deskriptiven Statistik sind Kennwerte (‘sample statistic’) exakt bestimmbar → sie beziehen sich nur auf die Stichprobe.
• In der inferenziellen Statistik wollen wir von den Kennwerten der Stichprobe auf die Parameter der Grundgesamtheit schließen.
• Stichprobenkenngrößen werden in der Inferenzstatistik als Zufallsvariable aufgefasst (da abhängig von zufällig gezogenen Stichprobe)
  • sie schwanken zufällig, aber zumindest um den ‘wahren’ Wert der Population.

Von der Stichprobe zur Grundgesamtheit | 2

Merkmal	Kennwert	Parameter
Mittelwert	\bar{X}	\mu (mü)
Varianz	s^2	\sigma^2 (sigma-qu.)
Standardabweichung	s	\sigma (sigma)
Korrelation	r	\rho (rho)
Anteilswert	h bzw. p	\pi (pi)

Schätzfunktionen

• sind die Basis zur Berechnung von Punktschätzungen und zur Bestimmung von Konfidenzintervallen mittels Intervallschätzern.
• werden als Teststatistiken in Hypothesentests verwendet.

Punktschätzer

• geben Näherungswert für gesuchten Populationsparameter.
• meist mit Angabe eines Maß für den Schätzfehler

• Beispiel:
  • Erwartungswert
  • Varianz
  • andere Verteilungsparameter (Median,.)
  • Regressionsparameter

Intervallschätzer

• geben Bereich an (= Konfidenzintervall), in dem der gesuchte Populationsparameter mit gewisser Wahrscheinlichkeit (Konfidenz) liegt.

Punktschätzung | Wie funktioniert das?

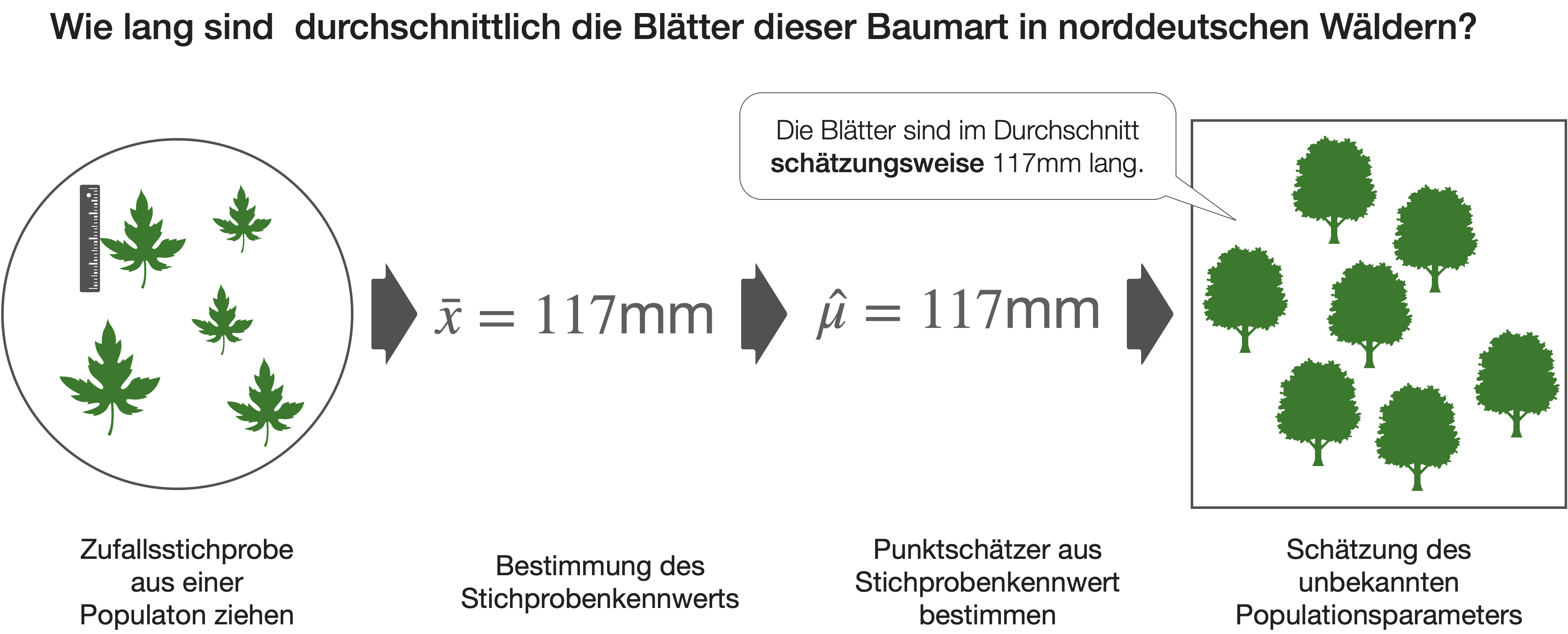
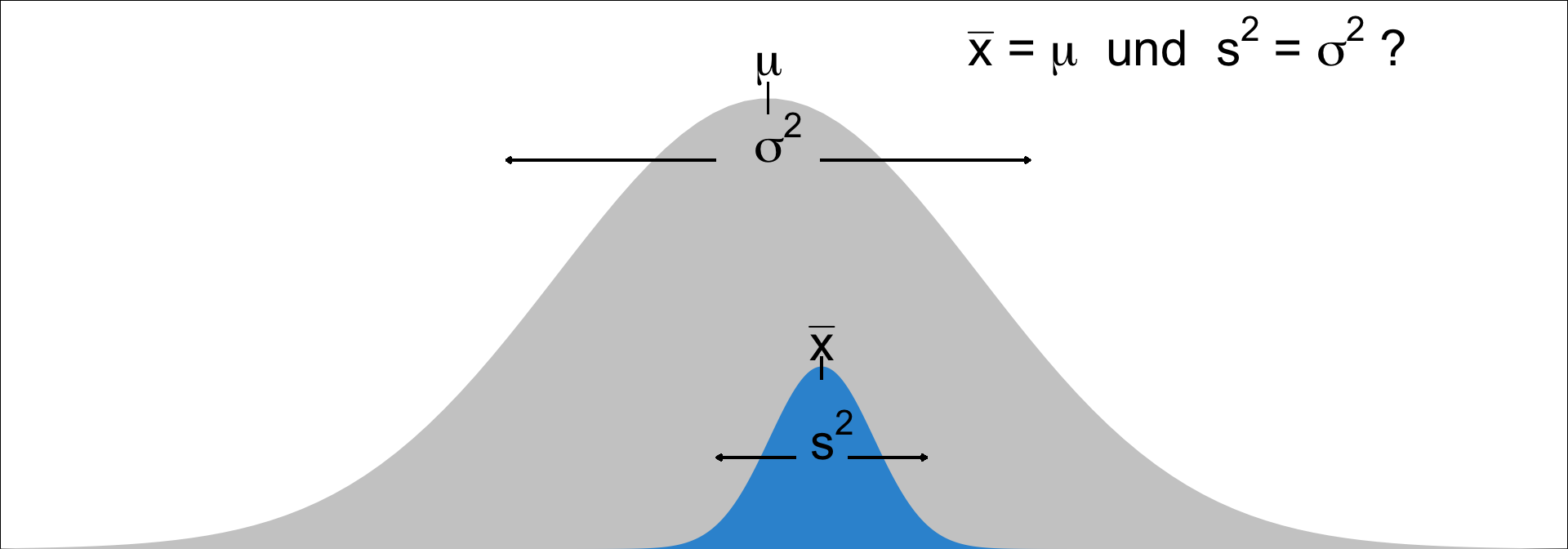
• Damit Stichprobenkennwerte als Punktschätzer genutzt werden können, müssen sie ‘erwartungstreu’ sein, d.h. keinen systematischen Fehler enthalten.
• → Dann entspricht z.B. der Mittelwert der Stichprobenverteilung (=Erwartungswert E(\bar{x})) dem Populationsmittelwert → und dann ist auch \bar{x} ein guter Schätzer für \mu.

Die Stichprobenkennwertverteilung | 1

Eine hypothetische Verteilung

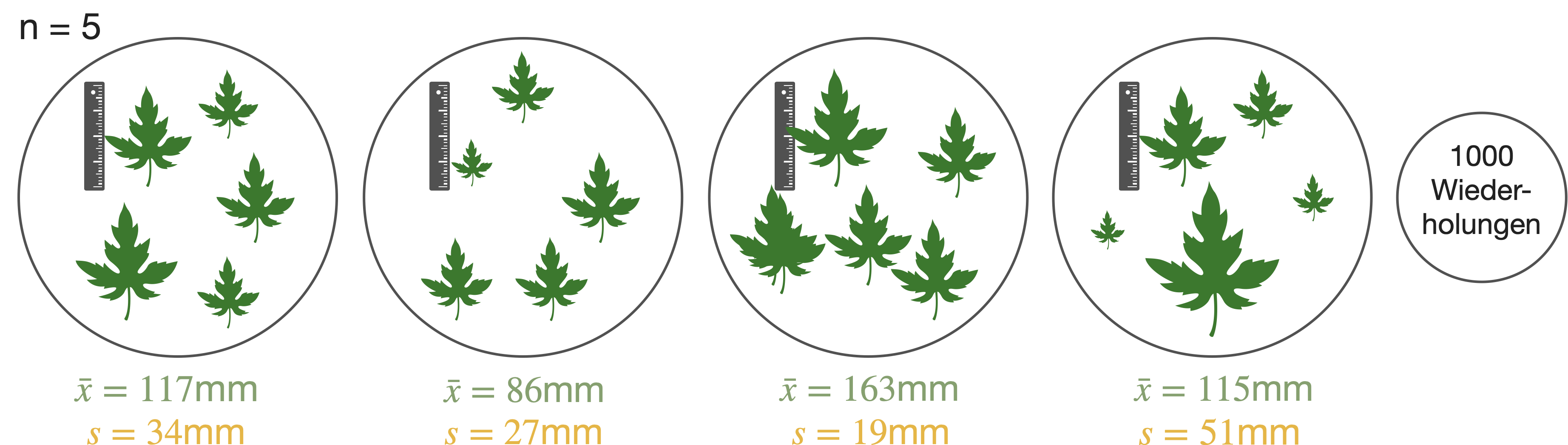
Die Stichprobenkennwertverteilung | 2

Einflussgrößen

Ihre Verteilung ist abhängig von

• der Verteilung des Merkmals in der Population.
• der Größe der Stichprobe (N).
• dem Typ des Kennwerts.
• der Art der Stichprobe (repräsentativ oder nicht).

Punktschätzung | Mittelwert

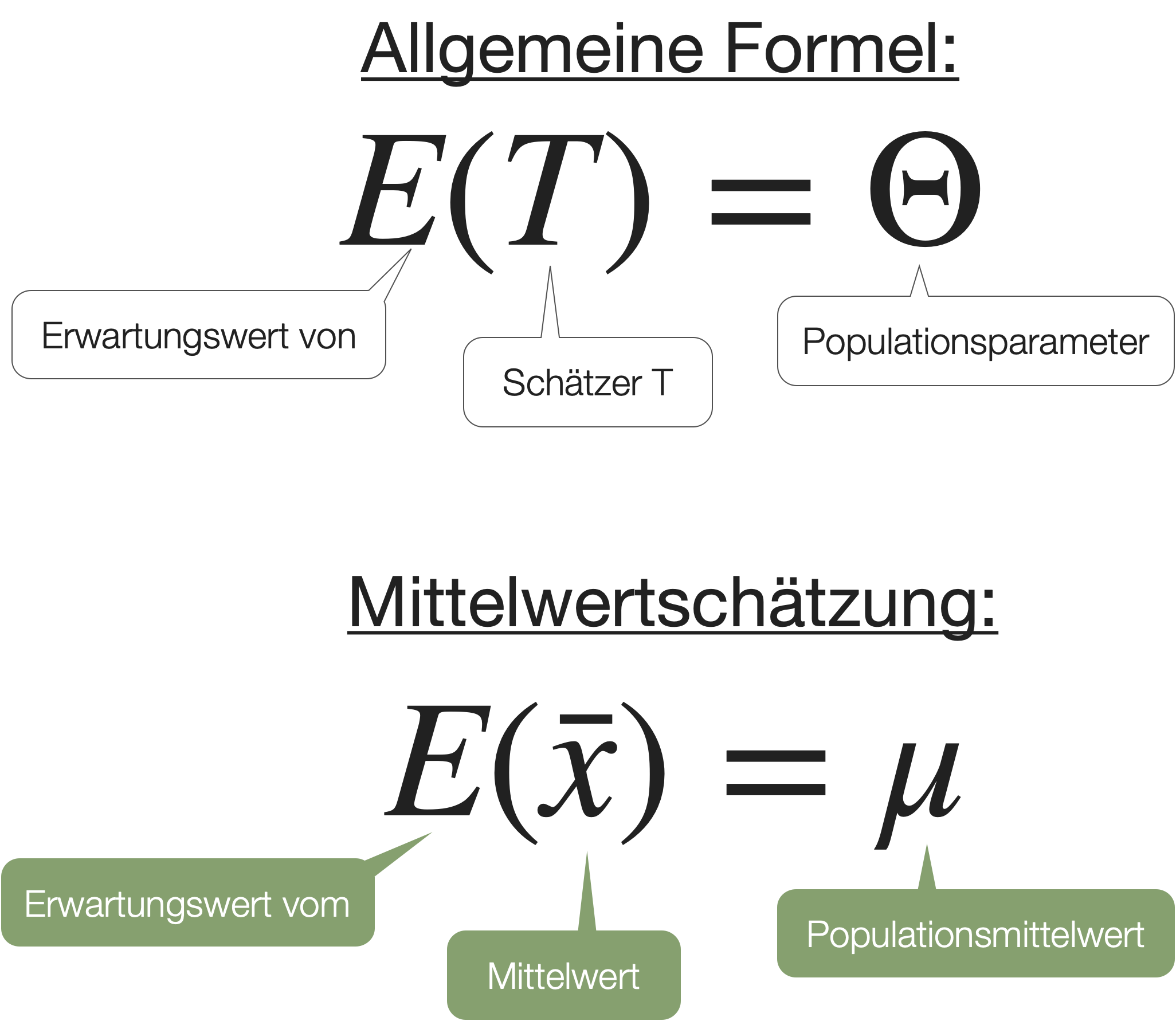
Beispiel mit \mu = 120\text{mm}

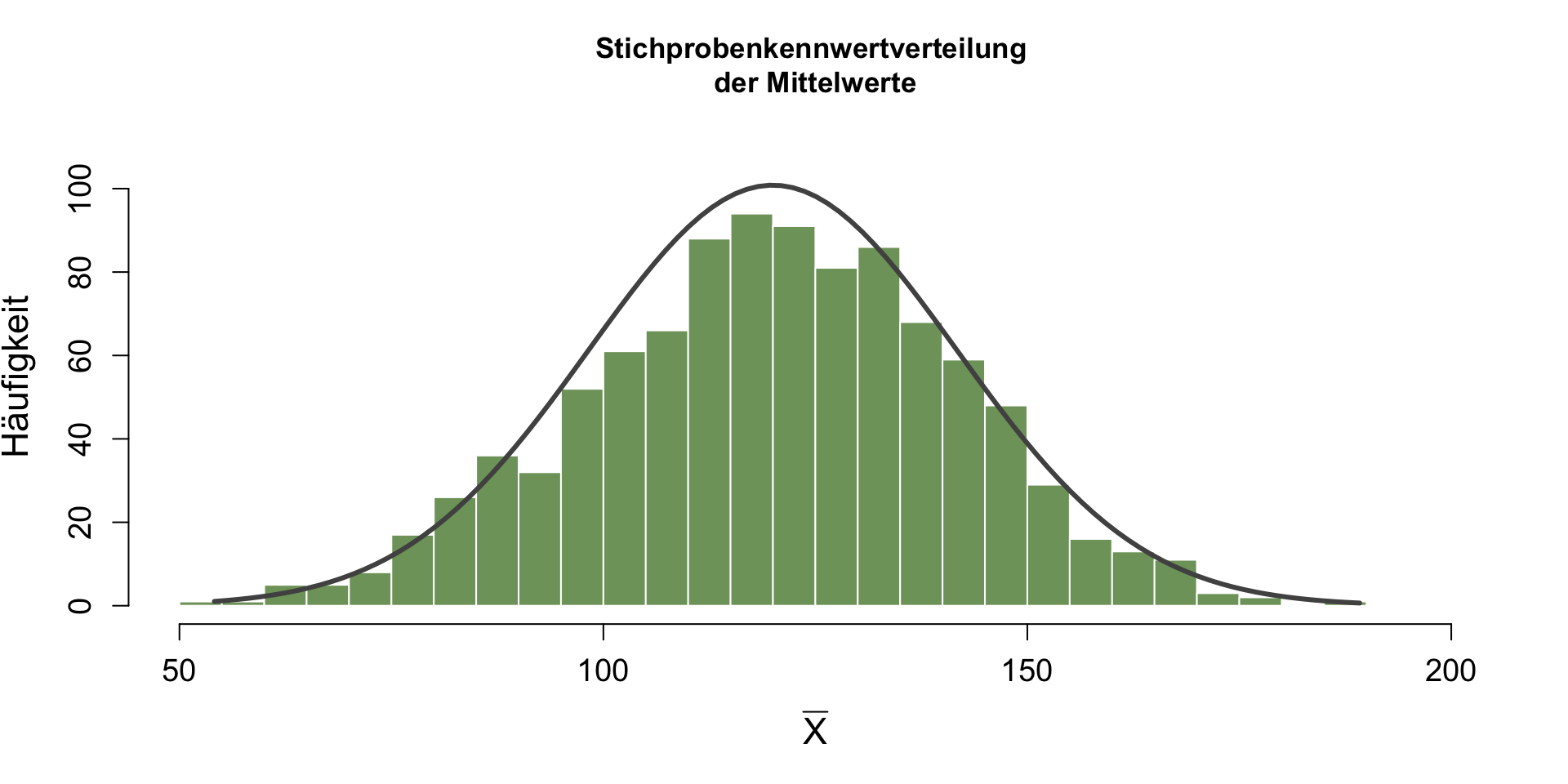
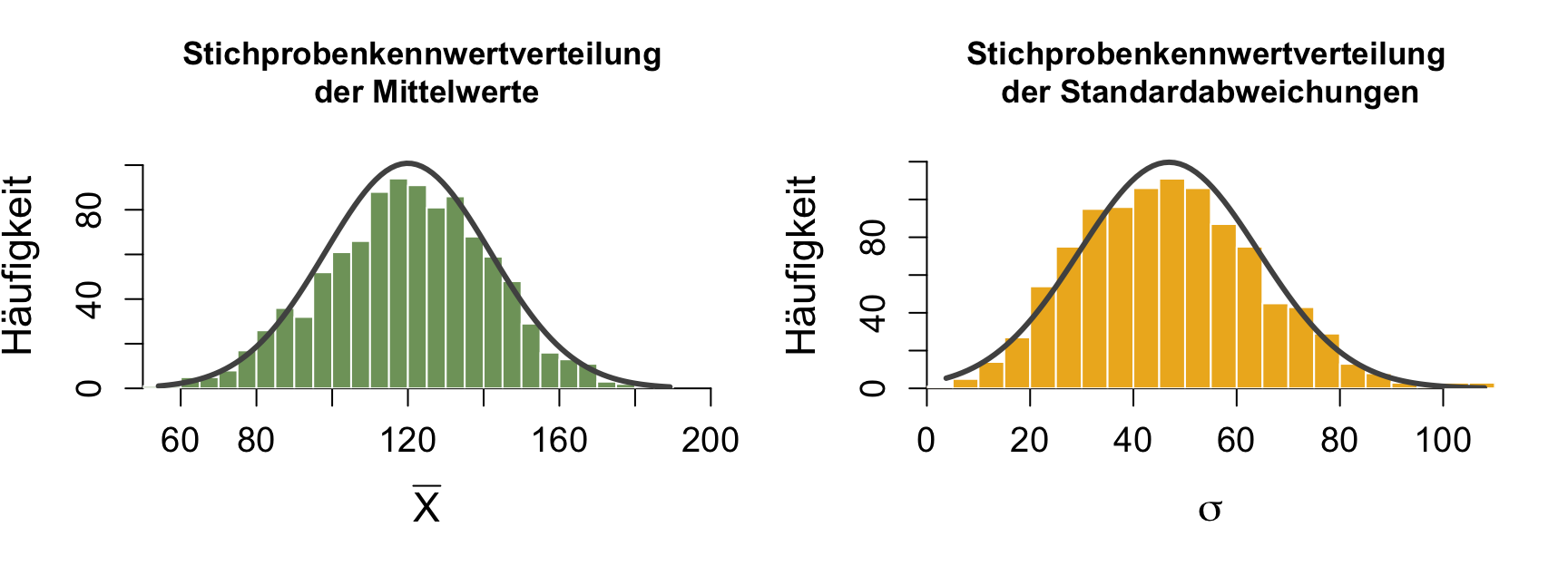
• Bei 1000 Proben mit je N = 5 ist Mittelwert der Stichprobenkennwertverteilung: E(\bar{x}) = 119.97 \text{mm}

Punktschätzung | Varianz 1

• Mittelwert der Varianzverteilung meist kleiner als ‘wahre’ Varianz → enthält weniger sehr unwahrscheinliche oder extreme Werte (BIAS)
• Lösung → mit Korrekturfaktor n/(n-1) multiplizieren:

\hat{\sigma}^2 = s^2\frac{n}{n-1} \Rightarrow E(\hat{\sigma}^2)=\sigma^2

\begin{align} \hat{\sigma}^2 &= \frac{\sum_{i=1}^{n}(X_i-\bar{X})^2}{n}\cdot\frac{n}{n-1}\nonumber\\ &=\frac{\sum_{i=1}^{n}(X_i-\bar{X})^2}{n-1}\nonumber\\ \end{align}

• Die R Funktion var() und die Excel/Calc Funktion =VARIANZ() berechnen die korrigierte Varianz.
• Bei Excel/Calc gibt es auch die Funktion =VAR.P() für die unkorrigierte Varianz.

Punktschätzung | Varianz 2

Beispiel mit \sigma^2 = 2500

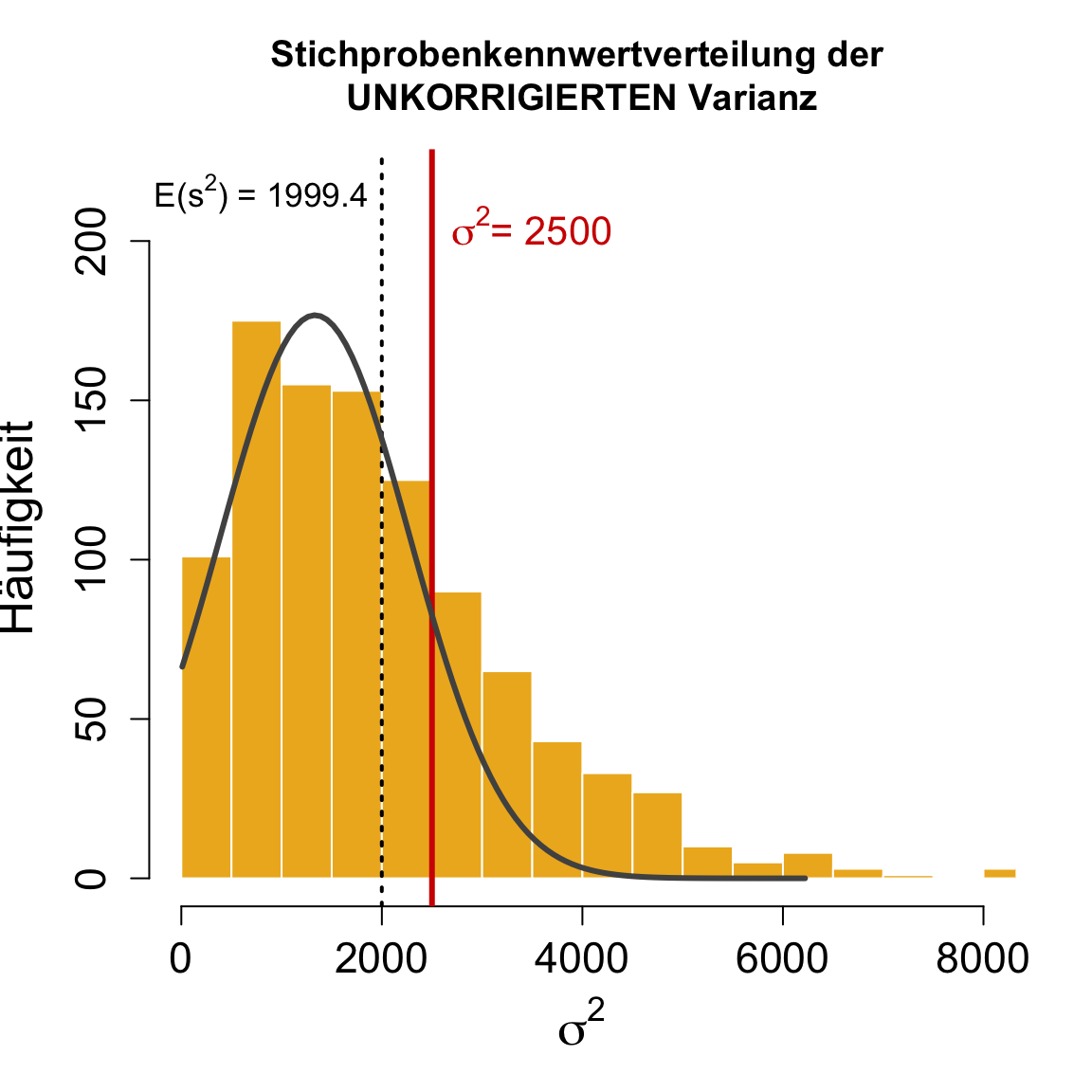
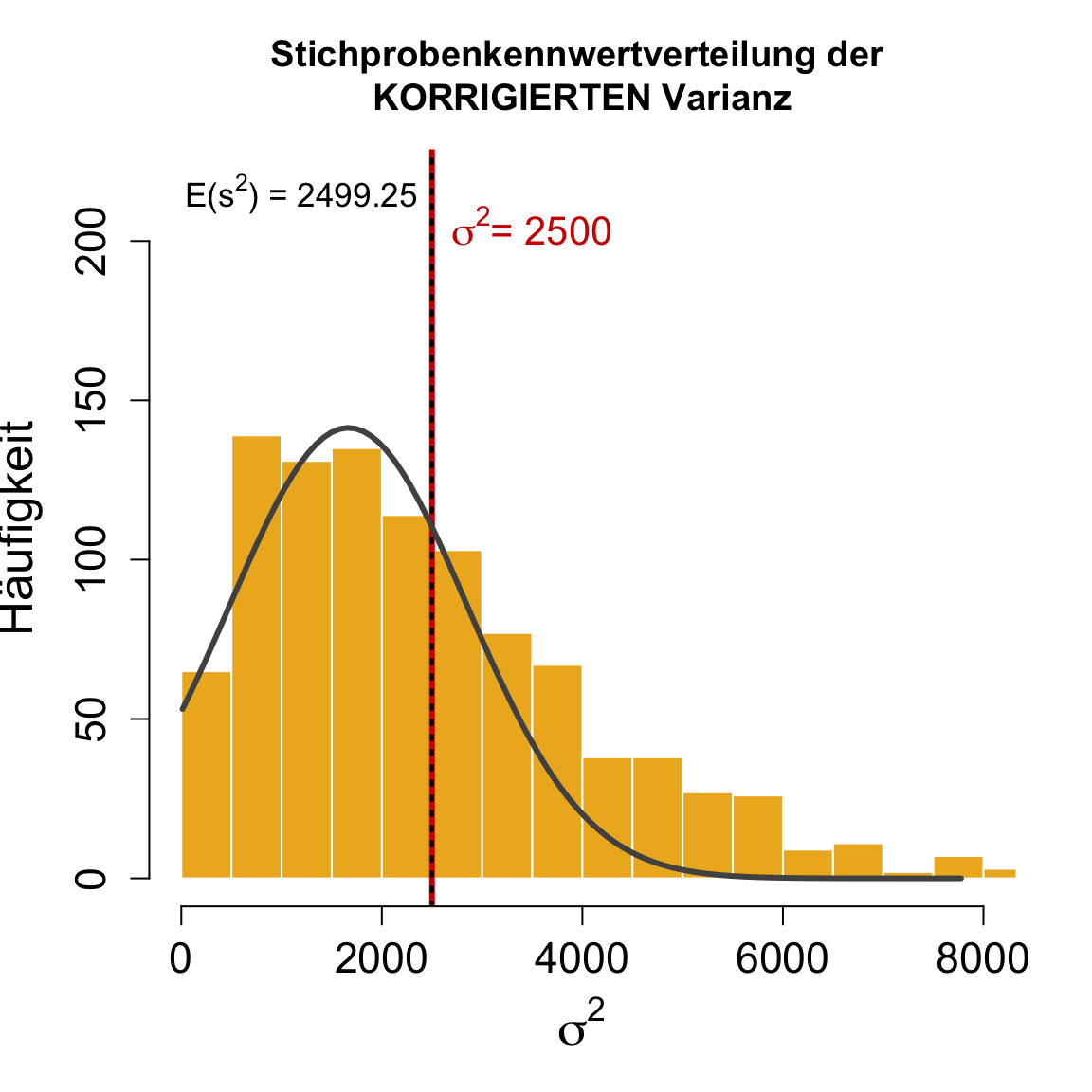
Standardschätzfehler

• Die Genauigkeit der Punktschätzung sollte immer angegeben werden. Das Maß dafür ist der Standardfehler des Schätzers.
• Je kleiner der Standardschätzfehler, desto größer ist die Effizienz des Schätzers.
• Der Standardfehler eines Kennwerts entspricht der Standardabweichung der Stichprobenkennwertverteilung.
• Der wichtigste ist der Standardfehler des Schätzers des Mittelwerts → wird beeinflusst durch die (geschätzte) Populationsvarianz und Stichprobengröße:

Mittelwert

\hat{\sigma}_{\bar{X}}=\sqrt\frac{\hat{\sigma}^2}{n}=\frac{\hat\sigma}{\sqrt{n}}

Median

\hat{\sigma}_{Md}=1.25\sqrt\frac{\hat{\sigma}^2}{n}

Standardabw.

\hat{\sigma}_{s}=\sqrt\frac{\hat{\sigma}^2}{2n}

Prozentwert

\hat{\sigma}_{\%}=\sqrt\frac{P\cdot Q}{n}

Konfidenzintervalle (KI)

Ausgangsfrage

• Wie präzise ist diese Schätzung von 117mm?
• Kann es denn sein, dass der wahre Populationsmittelwert auch 100mm oder 140mm ist und wir einfach Pech mit der Probe hatten?
• In welchem Bereich liegt der wahre Mittelwert höchstwahrscheinlich?

Diese Fragen kann ein Punktschätzer nicht beantworten – aber ein Intervallschätzer!

Intervallschätzung | 1

Übersicht

• Auf Basis einer Zufallsprobe wird der Bereich geschätzt, wo der gesuchte Populationsparameter liegen könnte.
• Ausgangspunkt ist immer eine Punktschätzung → dann wird ein (symmetrisches) Intervall bestimmt, das Konfidenzintervall KI
• Konfidenz wird als wiederholte Stichprobe interpretiert.
• Kann für jeden Parameter (z.B. Mittelwert, Varianz, Korrelationskoeffizient) berechnet werden.
• Die Breite des Intervalls hängt ab
  • vom Stichprobenumfang, der Varianz der Stichprobe und
  • der festgelegten Wahrscheinlichkeit (= Konfidenzniveau) → üblich: 90%, 95%, 99%
• Gegenwahrscheinlichkeit \alpha = Fehler, den wir bereit sind einzugehen.
  • Bei einem Konfidenzniveau von 95% ist \alpha = 1-0.95 = 0.05~~\text{bzw.} ~~5\%.

Intervallschätzung | 2

Konfidenzintervall

• KIs sind immer 2-seitig da Parameter immer größer oder kleiner als der Kennwert sein können:
  • 95% => 2.5% auf beiden Seiten.
• Grundsätzlich gilt: je höher die Konfidenz, desto breiter das Intervall.
• Zur Berechnung des KI wird der Standardfehler mit einer geeigneten statistischen Verteilung kombiniert, zum Beispiel
  • z und t für Mittelwerte,
  • \chi^2 für Varianzen.

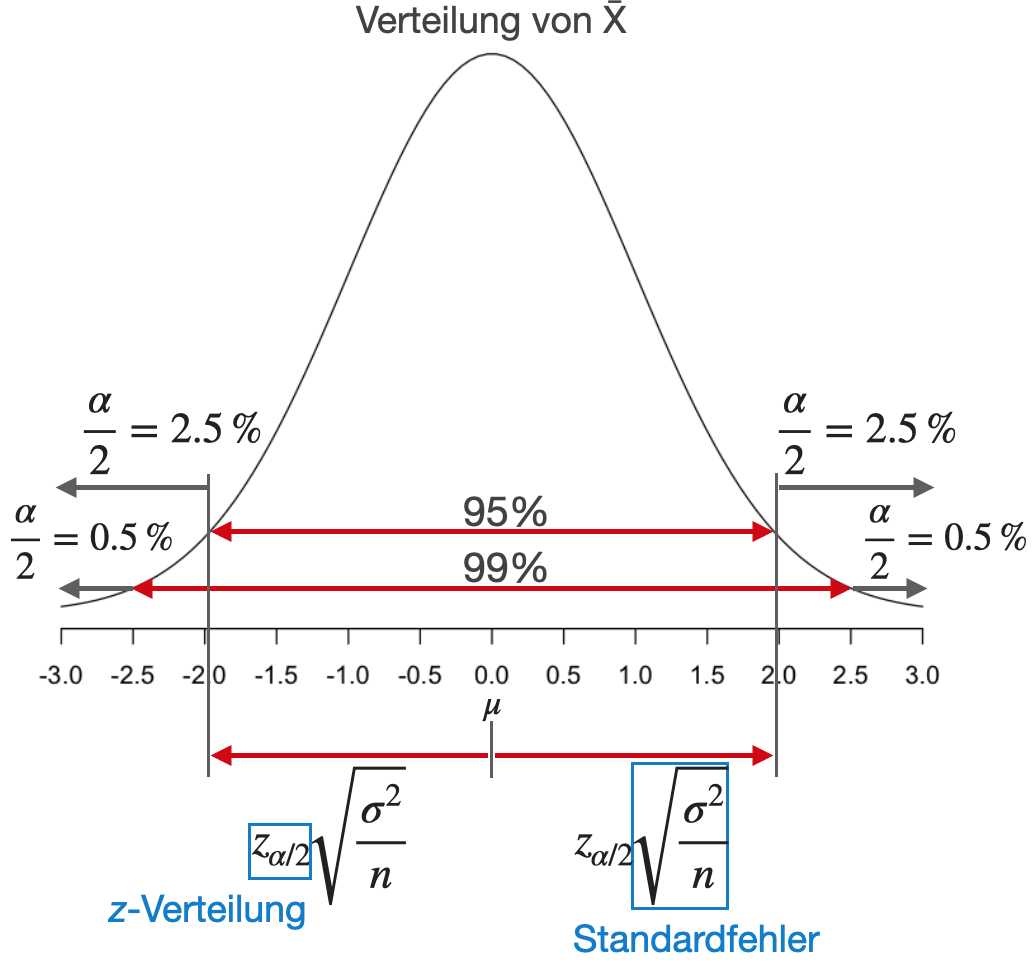
Im folgenden gehen wir drei Beispiele für die Konfidenzintervalle des Mittelwerts durch.

KI beruhend auf der Normalverteilung | n > 30

• Beruht auf einer Umstellung der Definition von Z.
• Nach dem zentralen Grenzwertsatz gilt für große Stichproben:
  • Der Bereich zwischen \mu und ± 1.96 mal dem Standardfehler enthält 95% aller Stichprobenmittelwerte.
  • Umkehrschluss: \mu ist in 95% aller Fälle nicht mehr als 1.96 Standardfehler vom Stichprobendurchschnitt entfernt: KI_{95\%} = \bar{X} \pm 1.96\sqrt\frac{\sigma2}{n}

Allgemeine Formel für ein beidseitiges Konfidenzintervall

(wenn die Populationsvarianz bekannt ist und eine Normalverteilung angenommen werden kann)

KI = z_{\alpha/2}\cdot\sqrt{\frac{\sigma^2}{n}} \Rightarrow P \{\bar{X}-z_{\alpha/2}\cdot\sqrt{\frac{\sigma^2}{n}}<\mu<\bar{X}+z_{\alpha/2}\cdot\sqrt{\frac{\sigma^2}{n}}\}

Bei KI_{90\%} ist z_{\alpha/2}=1.65, bei KI_{95\%} ist z_{\alpha/2}=1.96, bei KI_{99\%} ist z_{\alpha/2}=2.58

Berechnung in R: Große Stichprobe

Beispiel Blattlänge

\mu = 120\text{mm}, \sigma = 50\text{mm}

set.seed(123)
# Population
pop <- rnorm(10000000, 
  mean = 120, sd = 50)
# Stichprobe
big_sample <- sample(pop, 
  size = 500)

Normalverteilung bei N = 500

(big_mean <- mean(big_sample))

[1] 120

(big_se <- sd(big_sample)/sqrt(500))

[1] 2.1

(z_lower <- qnorm(p = 0.025, mean = 0, sd = 1))

[1] -1.96

(z_upper <- qnorm(p = 0.975, mean = 0, sd = 1))

[1] 1.96

(CI_lower <- z_lower*big_se)

[1] -4.12

(CI_upper <- z_upper*big_se)

[1] 4.12

→ Wir sind zu 95% sicher, dass der wahre Mittelwert im Bereich 115.90 - 124.10 liegt (120 ± 4.10).

KI beruhend auf der t-Verteilung | n < 30

• Die Normalverteilung kann nur verwendet werden bei großen Stichproben und wenn die Populationsvarianz bekannt ist. Meist ist dies nicht der Fall.
• Alternative: Multiplikation des Standardfehler des Stichprobenmittelwerts mit dem t-Wert statt dem z-Wert.
• Zuerst über die Formel t=\frac{\bar{X}-\mu}{S / \sqrt{n}} den t -Wert berechnen und dann (in der Tabelle oder mit R) t_{krit} und den p-Wert bestimmten.

Allgemeine Formel für ein beidseitiges Konfidenzintervall

KI_{95\%} = t_{(\alpha/2,df)}\sqrt{\frac{s^2}{n}} \Rightarrow P \{\bar{X}-t_{(\alpha/2,df)}\cdot\sqrt{\frac{s^2}{n}}\leq \mu \leq \bar{X}+t_{(\alpha/2,df)}\sqrt{\frac{s^2}{n}}\} = 0.95 (df = degrees of freedom: n-1)

Berechnung in R: Kleine Stichprobe | 1

Beispiel Blattlänge

\mu = 120\text{mm}, \sigma = 50\text{mm}

set.seed(123)
# Population
pop <- rnorm(10000000, 
  mean = 120, sd = 50)
# Stichprobe
small_sample <- sample(pop, 
  size = 5)

t-Verteilung bei N = 5

(small_mean <- mean(small_sample))

[1] 132

(small_se <- sd(small_sample)/sqrt(5) )

[1] 19.3

(t_lower <- qt(p = 0.025, df = 4)) # df=n-1

[1] -2.78

(t_upper <- qt(p = 0.975, df = 4))

[1] 2.78

(CI_lower <- t_lower*small_se)

[1] -53.6

(CI_upper <- t_upper*small_se)

[1] 53.6

→ Wir sind zu 95% sicher, dass der wahre Mittelwert im Bereich 78.30 - 185.50 liegt (131.90 ± 53.60).

Berechnung in R: Kleine Stichprobe | 2

Berechnung von t_{(\alpha,df)} mittels t-Tabelle für das Blattlängenbeispiel

Irrtumswahrscheinlichkeit für den zweiseitigen Test.

FG	0.5	0.2	0.1	0.05	0.025	0.01	0.005	0.002	0.001
1	1.000	3.08	6.31	12.706	25.45	63.66	127.32	318.31	636.62
2	0.816	1.89	2.92	4.303	6.21	9.93	14.09	22.33	31.60
3	0.765	1.64	2.35	3.182	4.18	5.84	7.45	10.21	12.92
4	0.741	1.53	2.13	2.776	3.50	4.60	5.60	7.17	8.61
5	0.727	1.48	2.02	2.571	3.16	4.03	4.77	5.89	6.87
10	0.700	1.37	1.81	2.228	2.63	3.17	3.58	4.14	4.59
15	0.691	1.34	1.75	2.131	2.49	2.95	3.29	3.73	4.07
20	0.687	1.32	1.73	2.086	2.42	2.85	3.15	3.55	3.85
30	0.683	1.31	1.70	2.042	2.36	2.75	3.03	3.38	3.65
40	0.681	1.30	1.68	2.021	2.33	2.70	2.97	3.31	3.55

Your turn …

03:00

Quiz: Vergleichen Sie die Konfidenzintervalle | 1

Wie groß ist das KI_{95\%} beim Zugverhalten verschiedener Vogelarten?

Buchfink

Grünfink

Mönchsgrasmücke

Bildquellen: Wikipedia (Buchfink und Grünfink unter CC BY-SA 2.5 Lizenz), Mönchsgrasmücke unter CC0 Lizenz)

Quiz: Vergleichen Sie die Konfidenzintervalle | 2

Statistiken der erhobenen Daten:

Kenngröße	Buchfink	Grünfink	Mönchsgrasmücke
Mittelwert x̅	1800 km	1950 km	3000 km
Standardabweichung s	±900 km	±400 km	±1000 km
Stichprobengröße n	20	10	30
t_{(\alpha, df)}	2.09	2.26	2.04

• Fragen
• Lösungscode

Da symmetrisches KI, nur Berechnung des oberen Bereichs

# Buchfink:
bf_se <- 900/sqrt(20)
bf_t <- qt(0.975, df = 20-1)
bf_ci <- round(bf_t*bf_se, 1)
paste0(1800-bf_ci, " - ", 1800+bf_ci, " (±", bf_ci, ")")

[1] "1378.8 - 2221.2 (±421.2)"

# Grünfink:
gf_se <- 400/sqrt(10)
gf_t <- qt(0.975, df = 10-1)
gf_ci <- round(gf_t*gf_se, 1)
paste0(1950-gf_ci, "-", 1950+gf_ci, " (±", gf_ci, ")")

[1] "1663.9-2236.1 (±286.1)"

# Mönchsgrasmücke:
mgm_se <- 1000/sqrt(30)
mgm_t <- qt(0.975, df = 30-1)
mgm_ci <- round(mgm_t*mgm_se, 1)
paste0(3000-mgm_ci, "-", 3000+mgm_ci, " (±", mgm_ci, ")")

[1] "2626.6-3373.4 (±373.4)"

Visualisierung des KI

• Wenn das 95% Konfidenzintervall (KI) der einen Stichprobe das KI der anderen nicht beinhaltet, kann man schlussfolgern, dass sich die Mittelwerte voneinander unterscheiden.

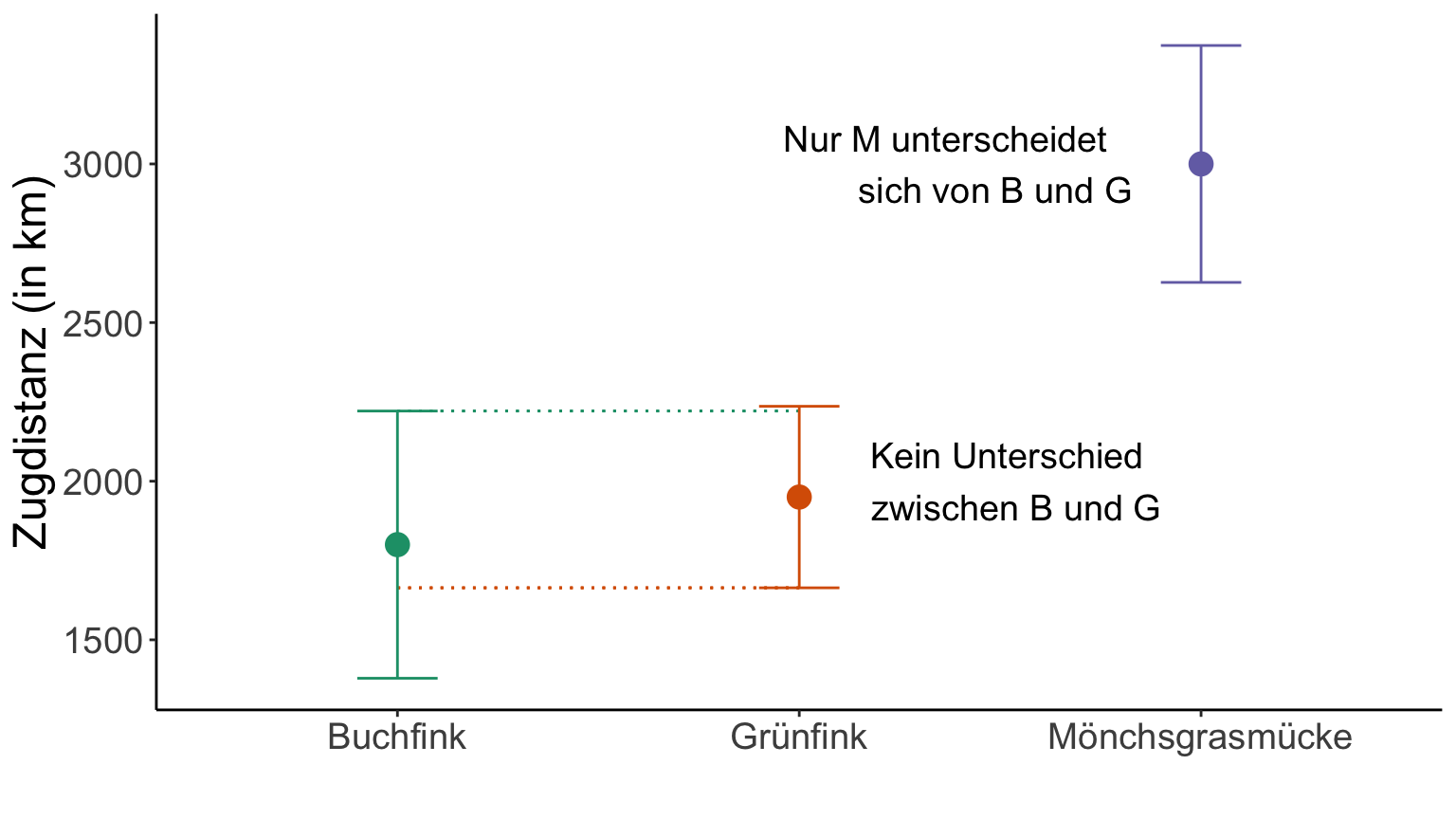
Berechnung des Stichprobenumfangs N

Bei Normalverteilung

Umformung der Formel zur Berechnung des KI des Mittelwerts nach der Stichprobe:

E = z_{\alpha/2}\sqrt\frac{\sigma^2}{n}

\Rightarrow~n=(\frac{z_{\alpha/2}\cdot\sigma}{E})^2

(E ist der maximale Schätzfehler)

Beispiel: Zugverhalten des Buchfink

Wie groß muss N sein, damit wir zu 99% sicher sind, dass der wahre Mittelwert im Bereich ±25 km (=E) um den Stichprobenmittelwert liegt?

• Bereits bekannt (aus vorheriger Studie):
  • \alpha = 0.01 → z_{\alpha/2}=2.58
  • \sigma = 900\text{ km}
  • E = 25\text{ km}

• n=(\frac{z_{\alpha/2}\cdot\sigma}{E})^2=(\frac{2.58\cdot 900}{25})^2 = 8599

Übungsaufgaben

Übungstag 2

Wahrscheinlichkeitsverteilungen und Schätzverfahren

• Aufgaben:
  • 2.1 Hausaufgabe zur Vorbereitung: zentraler Grenzwertsatz
  • 2.2 Standardnormalverteilung: Berechnung von Wahrscheinlichkeiten bei Hailängen
  • 2.3 Schätzverfahren: Konfidenzintervalle (KI) basierend auf Wahrscheinlichkeitsverteilungen
  • 2.4 Nachbereitung Fallstudie: Frage 1
• R Notebook-Skript:
  • DS2_02_Uebungen_Wahrscheinlichkeitsverteilungen_Schätzverfahren.Rmd

s. Handbuch - Abschnitt ‘Übungen’

Fragen?

Abschlussquiz

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de


Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.