
3-Wahrscheinlichkeitsverteilungen
Data Science 2
Saskia Otto & Monika Eberhard
Universität Hamburg, IMF & IZS
Sommersemester 2025
Lernziele
Nach Abschluss dieser VL und Übung werden Sie in der Lage sein (mit R) ..
- eine Wahrscheinlichkeitsverteilung für eine Zufallsvariable zu konstruieren.
- eine zufällige Stichprobe aus einer Population mit einer bestimmten Wahrscheinlichkeitsverteilung zu ziehen.
- Daten mittels Z-Transformation in eine Standardnormalverteilung zu überführen,
- Wahrscheinlichkeiten mittels Verteilungsfunktion (CDF) zu berechnen und
- die wichtigsten Prüfverteilungen stetiger Variablen unterscheiden zu können.
Einführung

Typen der Verteilung

Häufigkeitsverteilung (frequency distribution) = empirische V.
- Zeigt einfach nur an, wie oft ein Wert vorkommt (Ist-Werte).
- Die Darstellung der Realisationen x_i mit den dazugehörigen absoluten (h_i) bzw. relativen (h_i*N) Häufigkeiten erfolgt in grafischer oder tabellarischer Form.
Wahrscheinlichkeitsverteilung (probability distr.) = theoretische V.
- Zeigt an, wie häufig ein Wert hätte vorkommen sollen (Erwartungswerte).
- Jeder messbaren Teilmenge der möglichen Ergebnisse eines Zufallsexperiments wird eine Wahrscheinlichkeit zugeordnet.
- Der Erwartungswert einer Zufallsvariablen E(x) ist einfach der Mittelwert (µ) ihrer Wahrscheinlichkeitsverteilung.
- Kenntnis der Wahrscheinlichkeitsverteilung wichtig für viele statistischen Verfahren!
Übersicht wichtiger Wahrscheinlichkeitsverteilungen
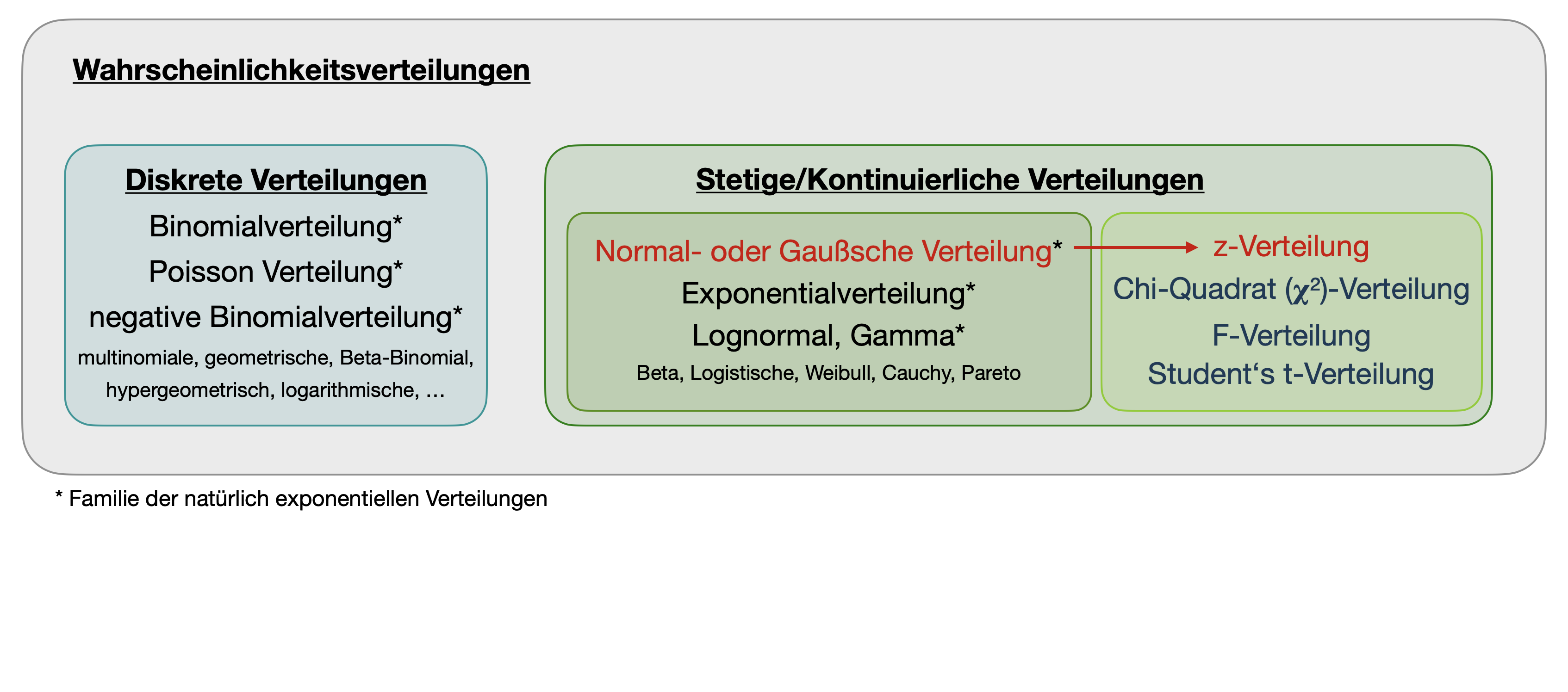
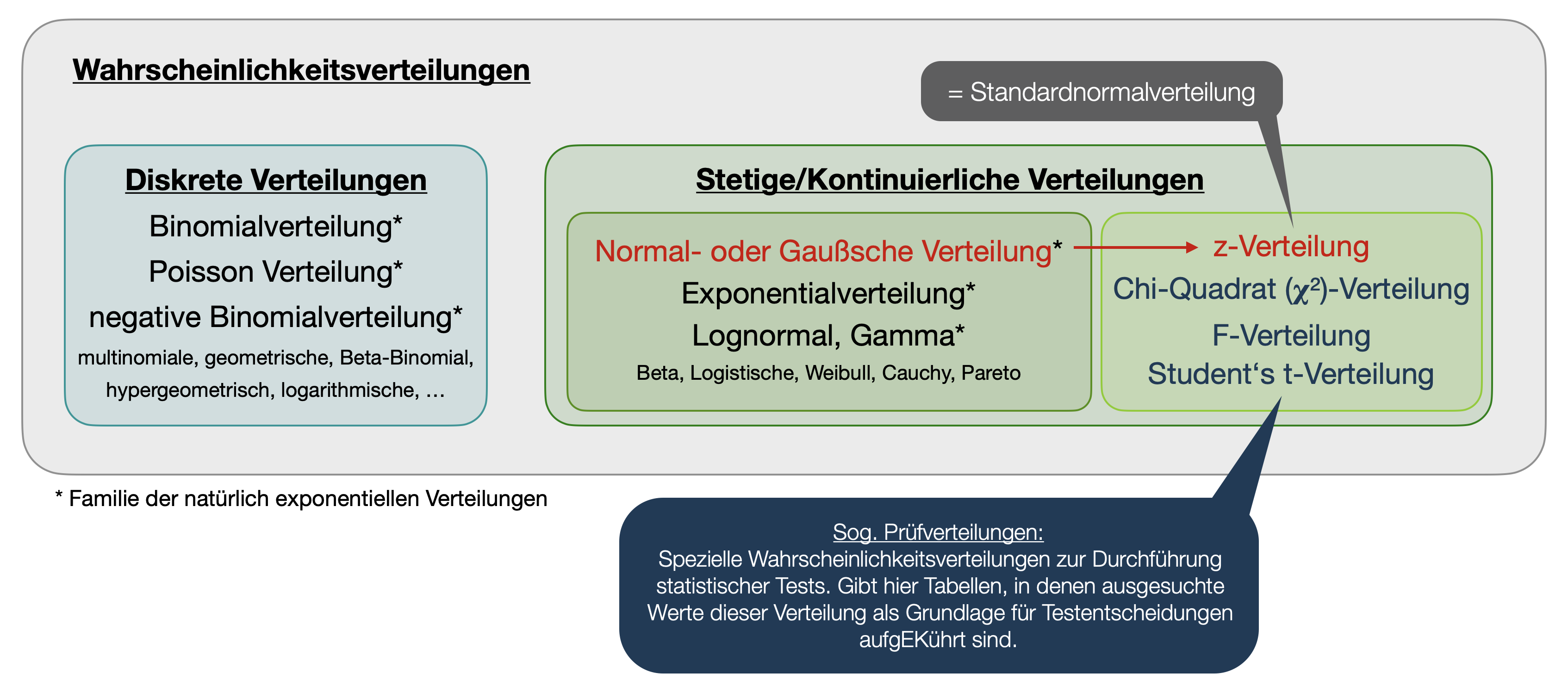
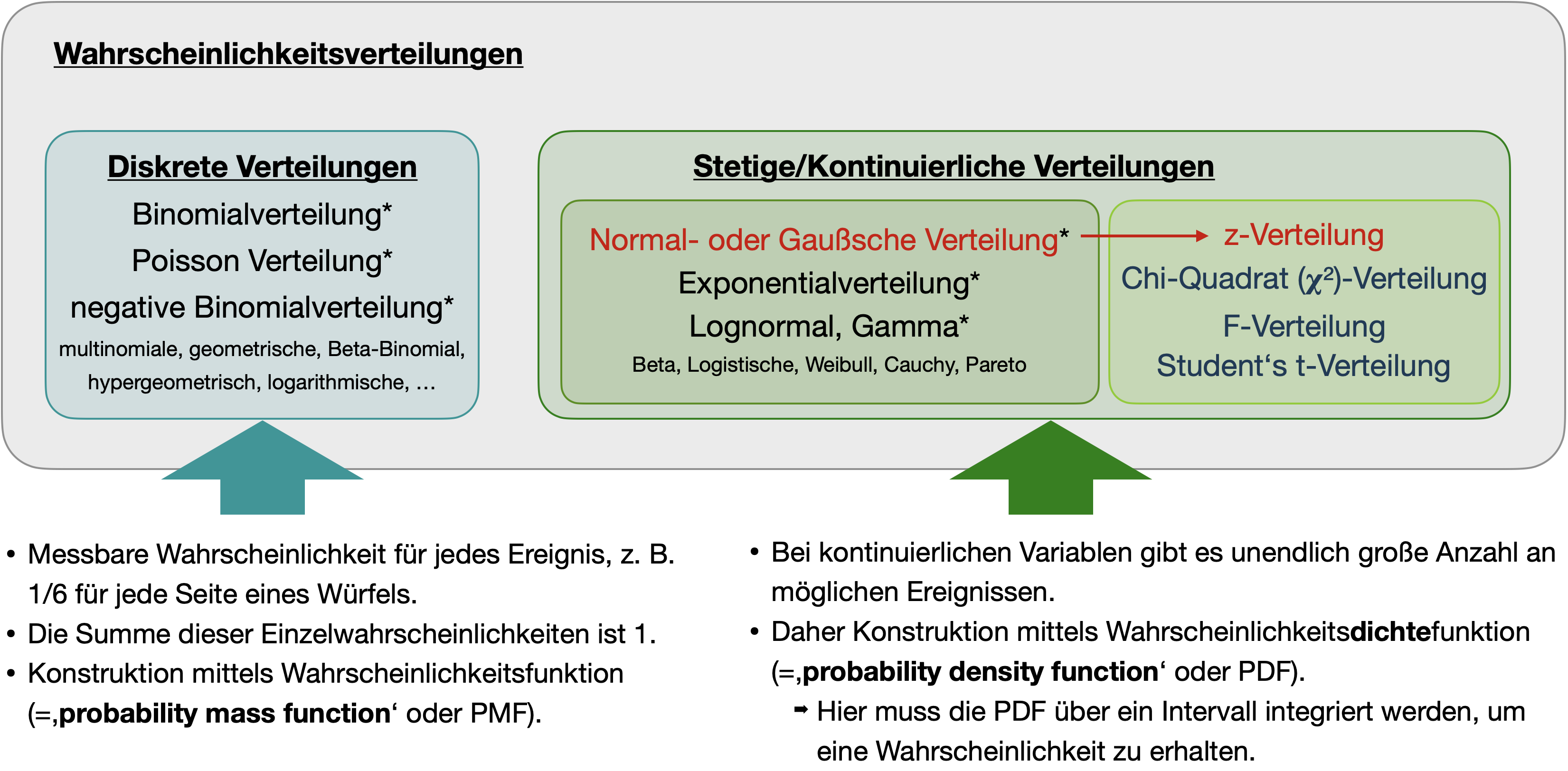
PMF vs. PDF
4 Verteilungen im Vergleich
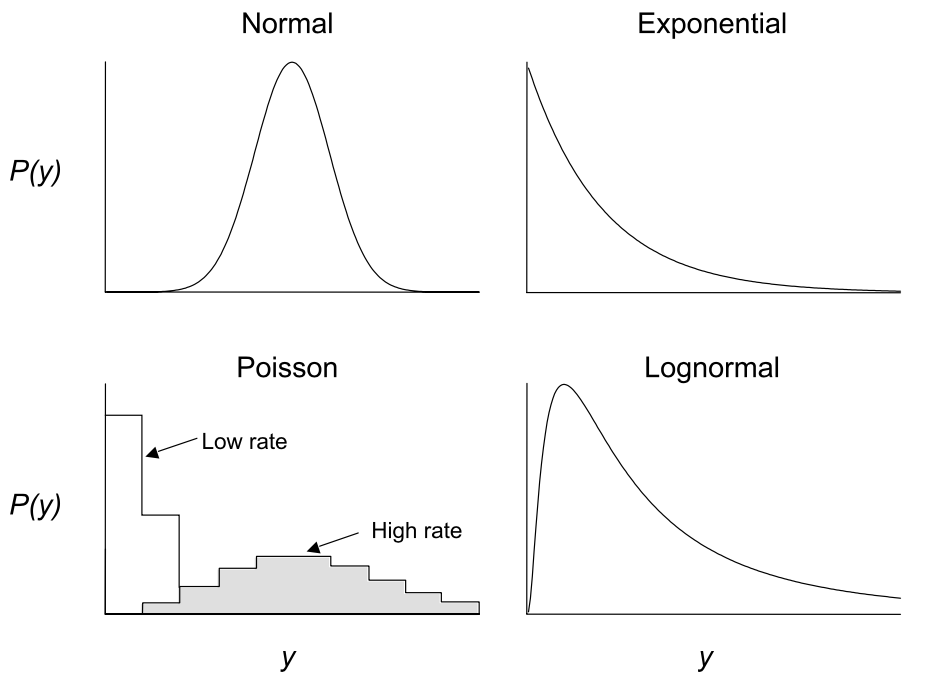
Bildquelle: Quinn & Keough (2002)
Experimentieren Sie selbst…
![]()
Bei welcher Stichprobengröße scheinen die Verteilungen stabil zu werden?
Link zur Shiny App: teaching-stats/distributions/distributions/
Die (Standard)Normalverteilung

Wichtigste Wahrscheinlichkeitsverteilung | 1
![]()
Hat 3 Eigenschaften
- Kontinuierliche, symmetrische Verteilung mit mehr Werten in der Mitte als am Rand (tails) → typische Glockenform (bell shape). Spannweite von -∞ bis +∞.
- Die Schiefe (skewness) ist null, da die Verteilung symmetrisch um den Mittelwert liegt.
- Zwei Parameter spezifizieren die Normalverteilung: Mittelwert und Varianz
Wichtigste Wahrscheinlichkeitsverteilung | 2
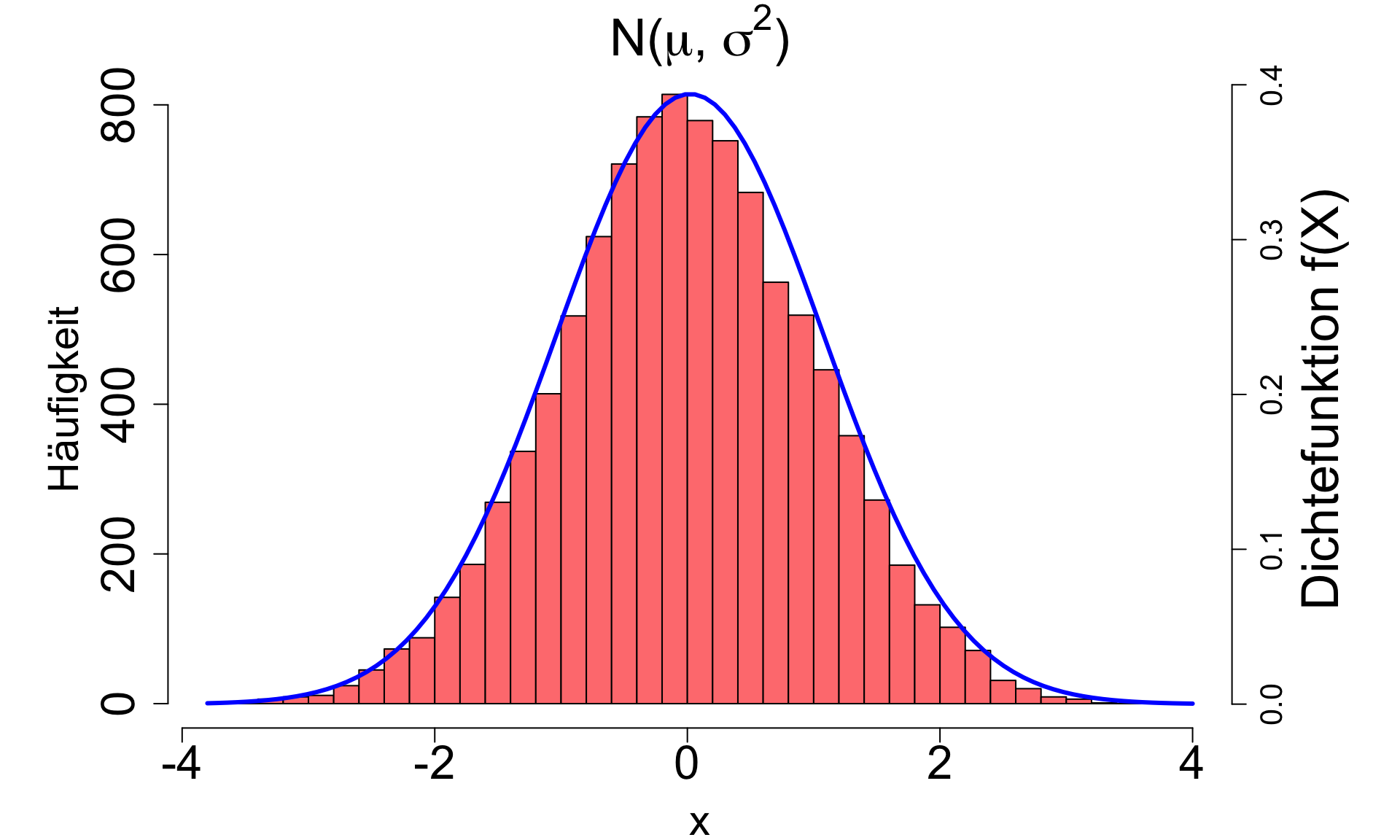
Gauß-Funktion (=PDF)
- Normalverteilungen sind durch folgende Formel beschrieben:
X \sim N(\mu_x, \sigma_x^2)
f(X)=\frac{1}{\sqrt{2\pi\sigma_x^2}}e^\frac{-(X-\mu_x)^2}{2\sigma_x^2}
- Beispiel: Mittelwert = 1, Varianz = 2
X \sim N(1, 2)
f(X)=\frac{1}{\sqrt{4\pi}}e^\frac{-(X-1)^2}{4}
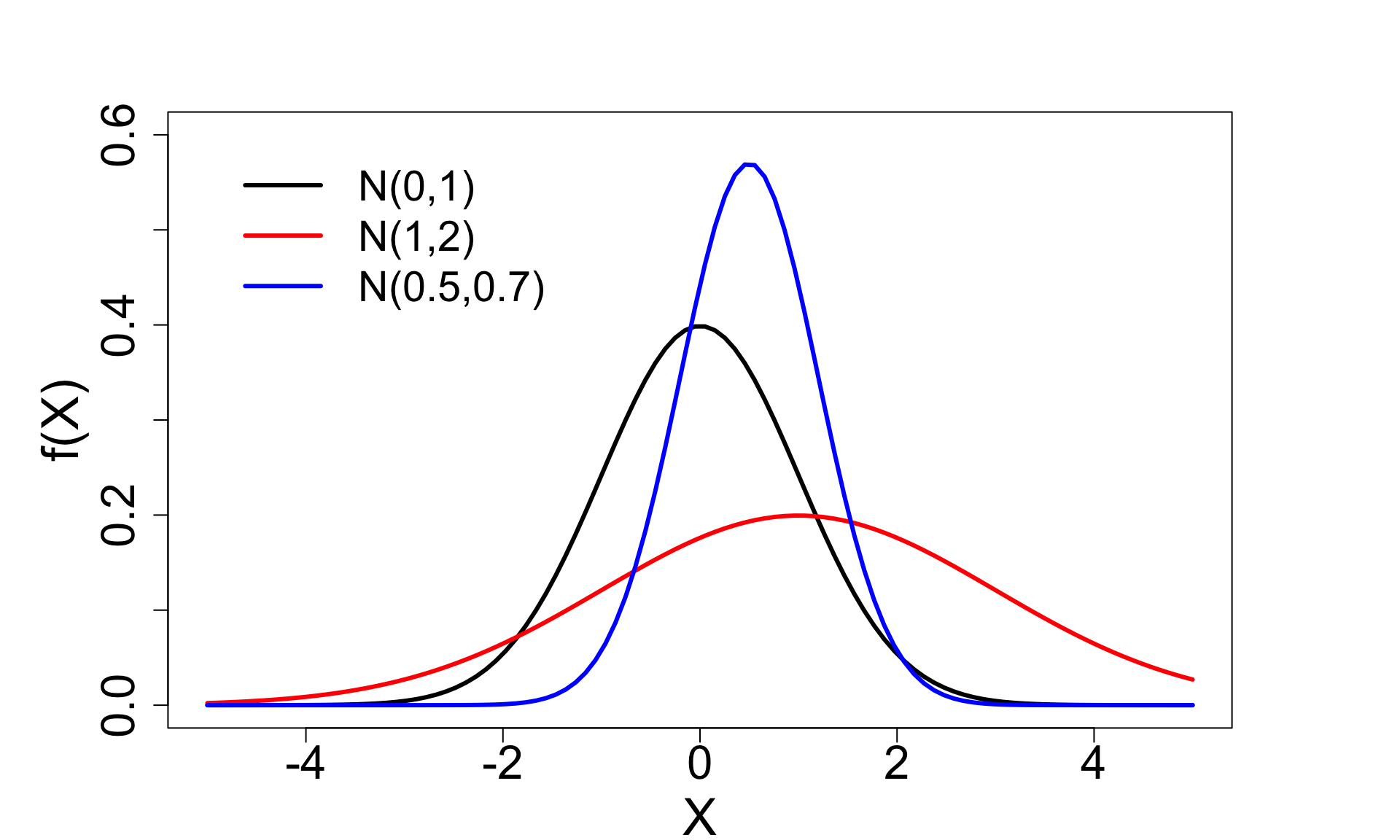
→ Erhöhen wir \mu, rücken wir die Kurve nach rechts.
→ Erhöhen wir \sigma^2 wird die Kurve flacher, verringern wir \sigma^2 wird die Kurve steiler.
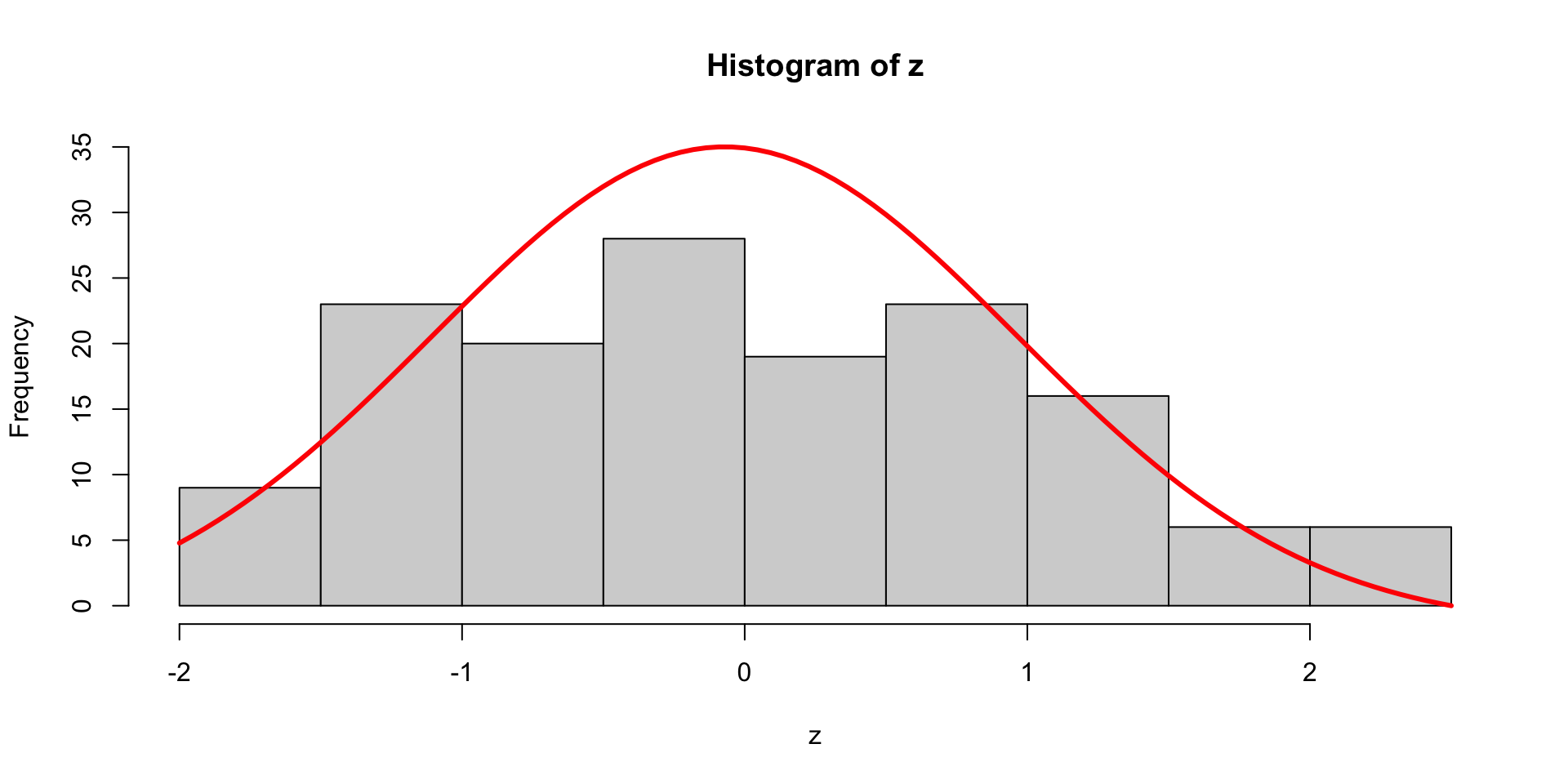
Normalverteilungen und Z-Transformation
- Da es unendlich viele mögliche Kombinationen von Mittelwert und Varianz gibt, gibt es eine unendliche Anzahl von möglichen Normalverteilungen.
- Durch die Z-Transformation lassen sie sich jedoch leicht in die sog. Standardnormalverteilung (oder z-Verteilung) überführen, bei der der Mittelwert = 0 und die Standardabweichung = 1 ist:
- Man nutzt die Tatsache, dass eine lineare Funktion einer normalverteilten Zufallsvariablen selbst wieder normalverteilt ist.
- Sprich, wenn X \sim N(\mu, \sigma^2) und Y=a+bX dann gilt Y \sim N(a+b\mu, b^2\sigma^2). Daraus ergibt sich:
Standardnormalverteilte Zufallsvariable Z
Z = \frac{X-\mu}{\sigma} \sim N(0,1)\Rightarrow z_i = \frac{x_i-\bar{x}}{s}
Dichtefunktion von Z
f(Z)=\frac{1}{\sqrt{2\pi}}e^\frac{-Z^2}{2}
Z-Transformation | Vorteil

Ein weiterer Vorteil der Z-Transformation (auch Standardisierung oder Normalisierung genannt):
- Sie überführt Werte, die mit unterschiedlichen Messinstrumenten erhoben wurden, in eine neue gemeinsame Einheit: in Standardabweichungs-Einheiten.
- Biologische und chemisch-physikalische Variablen können jetzt direkt verglichen werden.
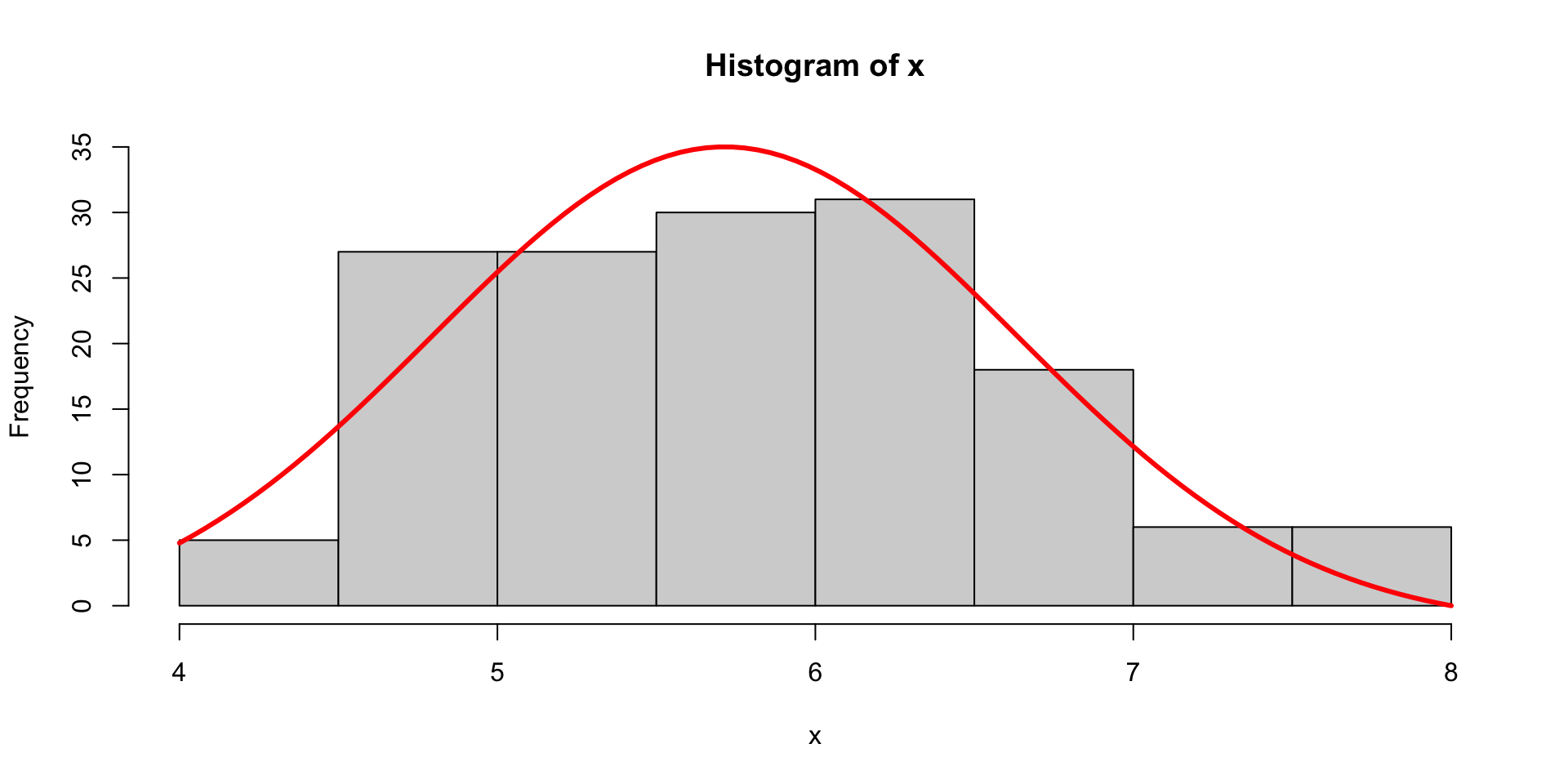
Z-Transformation | Beispiel Kronblattlänge im iris Datensatz
Aussagen über Wahrscheinlichkeiten
- Die Gesamtfläche unter der Normalkurve = Summe aller möglichen Ereignisse = 1 oder 100%.
- Die Fläche links oder rechts des Mittelwerts entspricht 50%.
- Die Wahrscheinlichkeit, dass ein Wert auftritt, der zwischen x_1 und x_2 liegt, entspricht dem Inhalt der Fläche unter der Kurve zwischen x1 und x2.
- Wenn man wissen möchte, mit welcher Wahrscheinlichkeit ein bestimmter Wert x_i auftritt, muss die PDF einer Standardnormalverteilung über ein Intervall integriert werden.
Dafür gibt es die sog. (kumulierte) Verteilungsfunktion, im Englischen die ‘cumulative density function’ (kurz CDF).
Die Verteilungsfunktion oder CDF
- Allgemein ist die Verteilungsfunktion des Wahrscheinlichkeitsmaß P definiert als: F_{P}(x)=P((-\infty ,x])
- → Die Funktion gibt an der Stelle x an, mit welcher Wahrscheinlichkeit ein Ergebnis aus der Menge (-\infty ,x]) (alle reellen Zahlen kleiner oder gleich x) eintritt.
- Für eine reelle Zufallsvariable X gilt: F_{X}(x)=P(X \leq x)
- Ausgedrückt als Integral der PDF f_X: F_X(x) = \int_{-\infty}^x f_X(x)dx
Die Wahrscheinlichkeit, dass X im Wertebereich (a ,b]) liegt, lässt sich dann wie folgt berechnen:
P(a < X \leq b) = F_X(b) - F_X(a) = \int_a^b f_X(x)dx
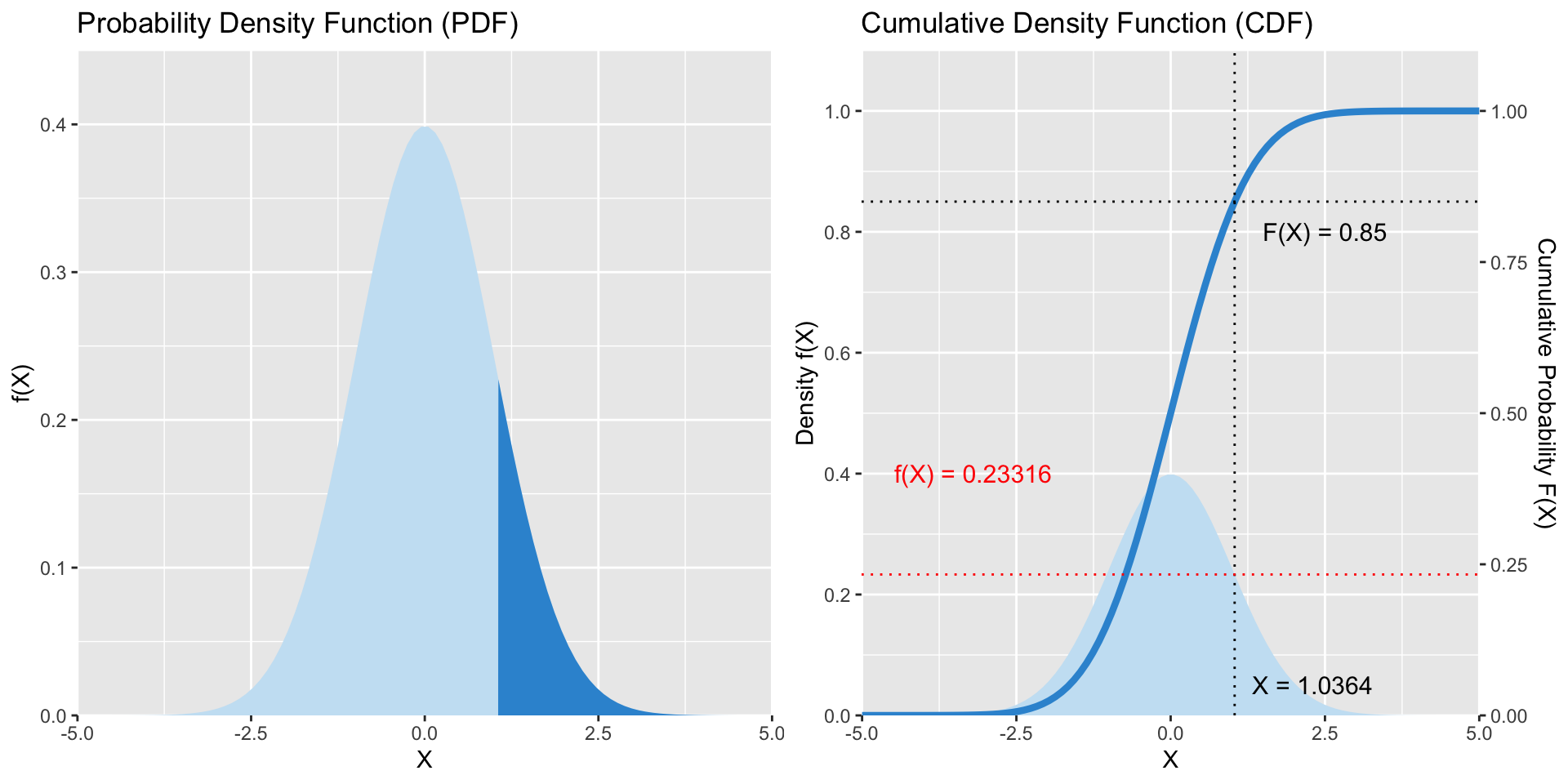
Die Verteilungsfunktion oder CDF | Beispiel
Wie groß muss X sein, damit 85% aller Werte darunter liegen?
Oder anders gefragt: Wie groß ist die Wahrscheinlichkeit, dass X ≤ 1.0364 ist?
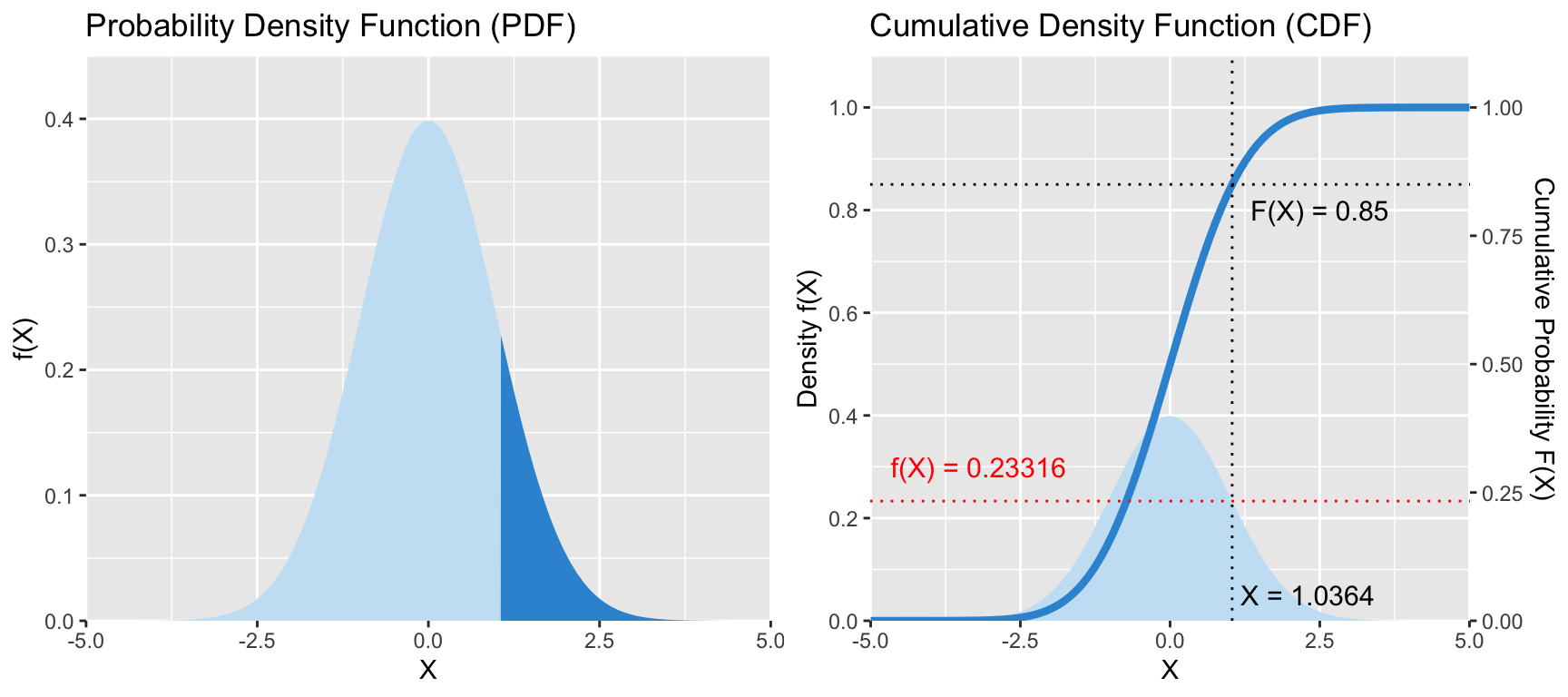
CDF
Die CDF ist eine S-förmige Kurve, die für jeden Wert von x die Wahrscheinlichkeit anzeigt, einen Stichprobenwert zu erhalten, der kleiner oder gleich x ist.
Die PDF repräsentiert die Steigung dieser Kurve (ihre “Ableitung”), welche niemals negativ ist. Die Steigung beginnt sehr flach (bei der Standardnormalverteilung bis etwa -2), steigt dann an bis zu einem Maximalwert (hier bei x = 0), wird dann flacher und oberhalb von x = +2 sogar sehr klein.
Streuintervalle | z-Tabelle
Aus einer Standardnormalverteilungs- tabelle kann abgelesen werden, dass bei normalverteilten Zufallsvariablen jeweils ungefähr
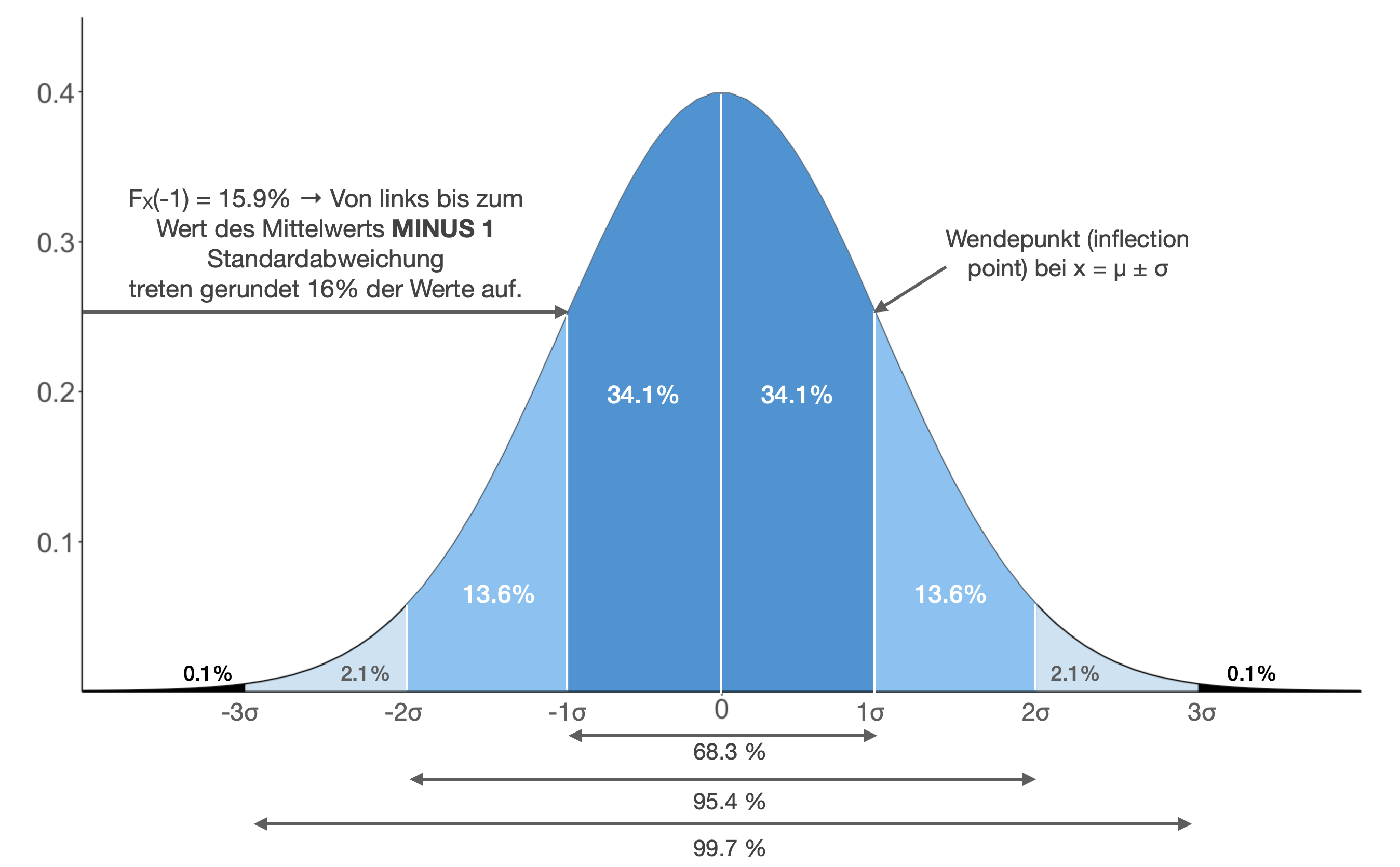
- 68.3 % der Realisierungen im Intervall \mu \pm \sigma,
- 95.4 % im Intervall \mu \pm 2\sigma und
- 99.7 % im Intervall \mu \pm 3\sigma liegen.
- 95% liegen zwischen \pm1.96\sigma und
99% zwischen \pm2.58\sigma- Beide Werte werden traditionell in Signifikanztest verwendet.
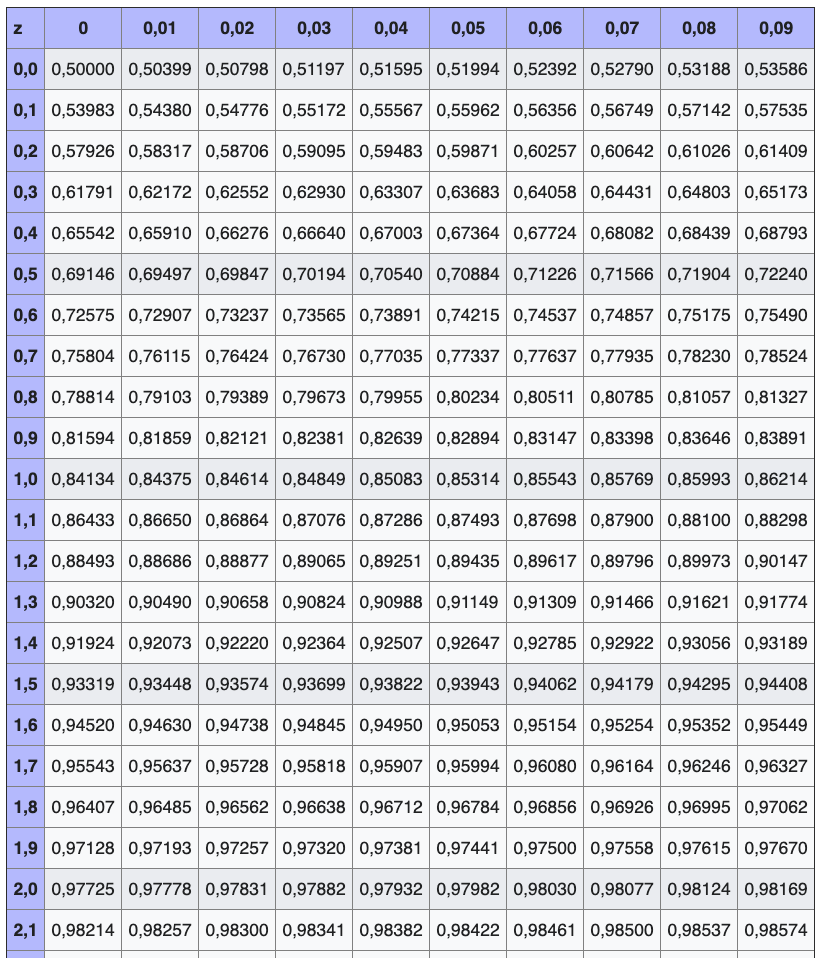
Quelle der Tabelle: Wikipedia
Streuintervalle | Grafisch
Die Normalverteilung in R


Die Normalverteilung in R | 4 Grundfunktionen
| Funktion | Zweck | Beispiel |
|---|---|---|
| rnorm() | Generiert zufällige Zahlen aus einer Normalverteilung | rnorm(n=100, mean=4, sd=7) → generiert 100 Zahlen aus einer NV mit \bar{x}=4 und \sigma = 7. |
| dnorm() | Probability Density Function | dnorm(x=0, mean=0, sd=.5) → Berechnet die Dichte (Höhe der PDF) für eine NV mit \bar{x}=0 und \sigma = 0.5. |
| pnorm() | Cumulative Density Function | pnorm(q=1.96, mean=0, sd=1, lower.tail=TRUE) → Berechnet die Fläche der Wahrscheinlichkeiten unter der Standardnormalkurve links von 1.96\sigma (für F_X(1.96)), d.h. ~0.975. |
| qnorm() | Quantile Function (Umkehrfunktion von pnorm) | qnorm(p=0.975, mean=0, sd=1, lower.tail=TRUE) → Gibt den Wert (die Quantile) zurück, bei dem die CDF der Standardnormalverteilung 0.975 ist, d.h. ~1.96. Alternative Schreibweise: qnorm(0.025, 0, 1, lower.tail = FALSE) |
Die Normalverteilung in R | Beispiel 1 pnorm()
Iris Kronblattlänge
Wie hoch ist die Wahrscheinlichkeit, dass eine zufällig ausgewählte Blume aus dem iris Datensatz eine Kronblattlänge von 6.1cm oder kleiner hat? Wir suchen also P(X ≤ 6.1) bei einem Stichprobemittelwert von 5.84 und einer Standardabweichung von 0.828.
Z=\frac{x-\mu}{\sigma}=\frac{6.1-5.84}{0.828}=0.314
Ergebnis: P(Z \leq 0.314) \approx 0.622
Die Normalverteilung in R | Beispiel 2 pnorm()
Iris Kronblattlänge
Und wie hoch ist die Wahrscheinlichkeit, dass eine zufällig ausgewählte Blume aus dem iris Datensatz eine Kronblattlänge von 5.3cm oder größer hat? Wir suchen also P(X ≥ 5.3):
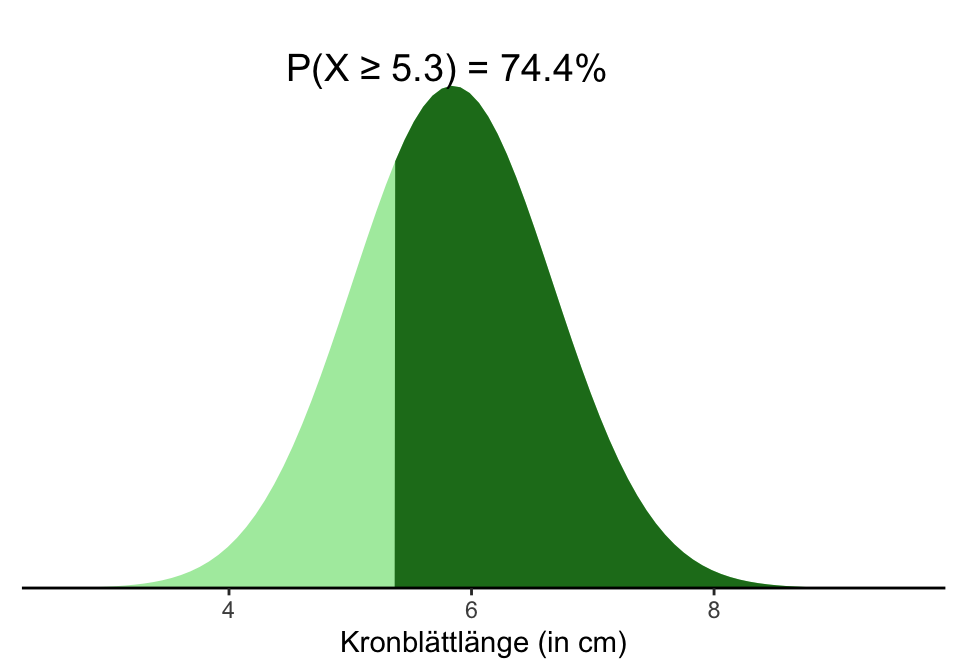
Die Normalverteilung in R | Beispiel 3
Zurück zu folgendem Beispiel
- Wie groß ist die Wahrscheinlichkeit, dass X ≤ 1.0364 ist
- Wie groß muss X sein, damit 85% aller Werte darunter liegen?
- Wie hoch ist f_X(1.0364)?
Die 4 Grundfunktionen bei anderen Verteilungen
?Distributions
| Verteilung | p.. | q.. | d.. | r.. |
|---|---|---|---|---|
| Normal | pnorm | qnorm | dnorm | rnorm |
| Student t | pt | qt | dt | rt |
| F | pf | qf | df | rf |
| Chi-Square | pchisq | qchisq | dchisq | rchisq |
| Binomial | pbinom | qbinom | dbinom | rbinom |
| Poisson | ppois | qpois | dpois | rpois |
| Negative Binomial | pnbinom | qnbinom | dnbinom | rnbinom |
| Geometric | pgeom | qgeom | dgeom | rgeom |
| Hypergeometric | phyper | qhyper | dhyper | rhyper |
| Uniform | punif | qunif | dunif | runif |
| Exponential | pexp | qexp | dexp | rexp |
| Log Normal | plnorm | qlnorm | dlnorm | rlnorm |
| Gamma | pgamma | qgamma | dgamma | rgamma |
| Beta | pbeta | qbeta | dbeta | rbeta |
Der zentrale Grenzwertsatz (‘Central Limit Theorem’)

Definition
![]()
Zentraler Grenzwertsatz - zentrales Grenzwerttheorem
- Mit wachsendem Stichprobenumfang (n) nähert sich die Stichprobenkennverteilung (= Verteilung von Stichprobenkenngrößen wie Mittelwert) an die Normalverteilung, unabhängig von der Form der Populationsverteilung.
- Die Mittelwerte von Stichproben streuen um den Mittelwert ihrer Grundgesamtheit, je größer n desto geringer die Streuung.
- Ist die Grundgesamtheit bereits normalverteilt so ist die Streuung der Mittelwerte relativ gering.
- Der Standardfehler (die Standardabweichung der Stichprobenmittelwerte) nähert sich mit hohen n der Standardabweichung der Grundgesamtheit geteilt durch die Quadratwurzel des Stichprobenumfangs.
Demonstration | Shiny App
![]()
Prüfverteilungen stetiger Variablen

Student’s t-Verteilung


Name stammt von William Sealey Gosset ab
(unter Pseudonym Student 1908 veröffentlicht).

- Forschte für die Guinness Brauerei.
- → Fand heraus, dass standardisierte Mittelwerte normalverteilter Daten nicht mehr normalverteilt, wenn \sigma^2 unbekannt ist und mit s^2 geschätzt werden muss.
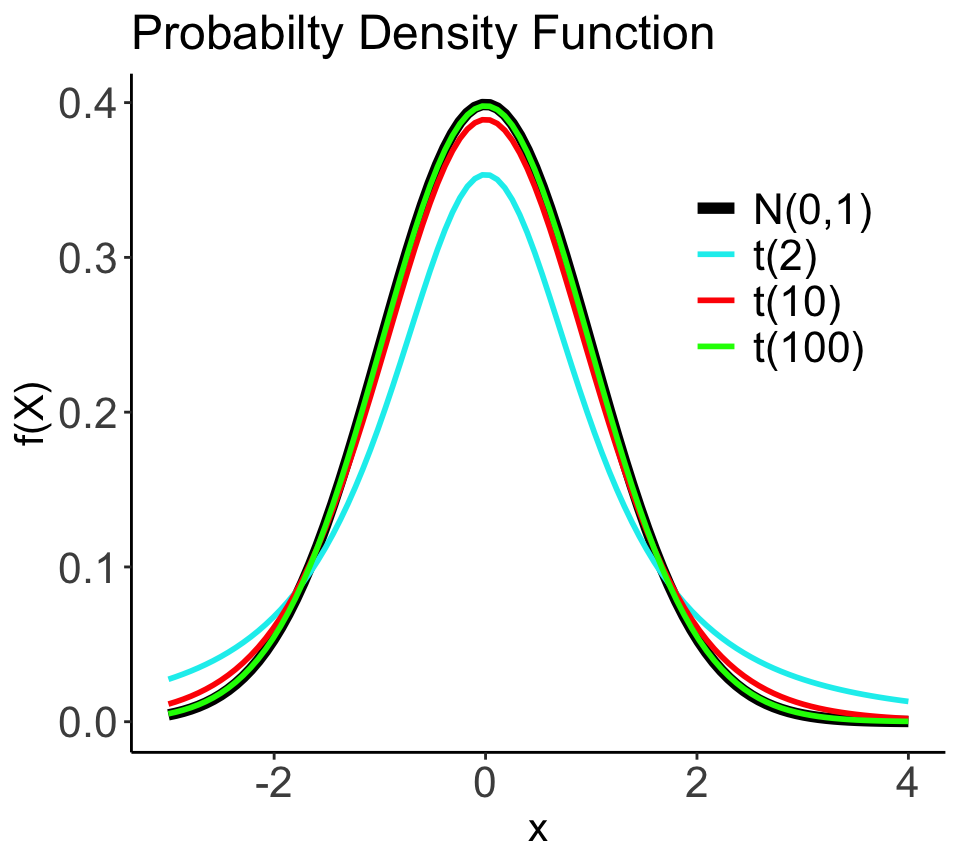
Student’s t-Verteilung | Eigenschaften
X ~ t(FG)
- Wie Standardnormalverteilung, nur etwas flacher (heavy-tailed) → kritische Werte sind hier größer!
- 1 Parameter (=Freiheitsgrad: n-1) der die Kurvenform bestimmt → mit wachsendem FG nähert sie sich einer Standardnormalverteilung.
- Verwendung für
- Konfidenzintervalle einzelner Parameter (z.B. Mittelwerte)
- Hypothesentest (t-Tests): Lineare Regression und Vergleich zweier Gruppenmittelwerte
Student’s t-Verteilung | Theorie
Oder: Wie die Student’sche Verteilung aus der Stichprobe hervorgeht
- Angenommen X_1, X_2,..X_n ist eine zufällige Stichprobe (z.B. Körpergewicht von Kegelrobben) aus einer normalverteilten Population mit dem erwarteten Mittelwert \mu und der Varianz \sigma^2, dann gilt \bar{X} = \frac{1}{n}\sum_{i=1}^{n}X_i~~\text{und}~~S^2=\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar{X})^2
- Für die zufällige Variable Z (also die standardisierte Variable) gilt dann: Z=\frac{\bar{X}-\mu}{\sigma} ~~\sim N(0,1)
- Wenn wir aber die Varianz (und entsprechend Standardabweichung) der Population nicht kennen, müssen wir stattdessen die Sichprobenstandardabweichung unter Berücksichtungung der Stichprobengröße (d.h. den Standardfehler) nehmen: t=\frac{\bar{X}-\mu}{\frac{S}{\sqrt{n}}} ~~\sim t(n-1)
Student’s t-Verteilung | Simulation
Empirischer Vergleich der Z-Verteilung vs. t-Verteilung
Code
calc_z_t <- function(n = 10, rep = 1000,
mu = 10, sigma = 1) {
z <- numeric(length = rep)
t <- numeric(length = rep)
for(i in 1:rep) {
x <- rnorm(n, mean = mu, sd = sigma)
x_m <- mean(x)
x_sd <- sd(x)
# z-score
z[i] <- (x_m-mu) / (sigma/sqrt(n))
# t-score
t[i] <- (x_m-mu) / (x_sd/sqrt(n))
}
out <- list(z = z, t = t)
return(out)
}
set.seed(321)
run_3 <- calc_z_t(n = 3)
run_5 <- calc_z_t(n = 5)
run_10 <- calc_z_t(n = 10)
run_30 <- calc_z_t(n = 30)
par(mfrow = c(2,4))
hist(run_3$z, breaks = 20, xlab = "x", main = "Z (n = 2)", xlim = c(-10,10))
hist(run_5$z, breaks = 20, xlab = "x", main = "Z (n = 5)", xlim = c(-10,10))
hist(run_10$z, breaks = 20, xlab = "x", main = "Z (n = 10)", xlim = c(-10,10))
hist(run_30$z, breaks = 20, xlab = "x", main = "Z (n = 30)", xlim = c(-10,10))
hist(run_3$t, breaks = 50, xlab = "x", main = "t (n = 2)", xlim = c(-10,10))
hist(run_5$t, breaks = 20, xlab = "x", main = "t (n = 5)", xlim = c(-10,10))
hist(run_10$t, breaks = 20, xlab = "x", main = "t (n = 10)", xlim = c(-10,10))
hist(run_30$t, breaks = 20, xlab = "x", main = "t (n = 30)", xlim = c(-10,10))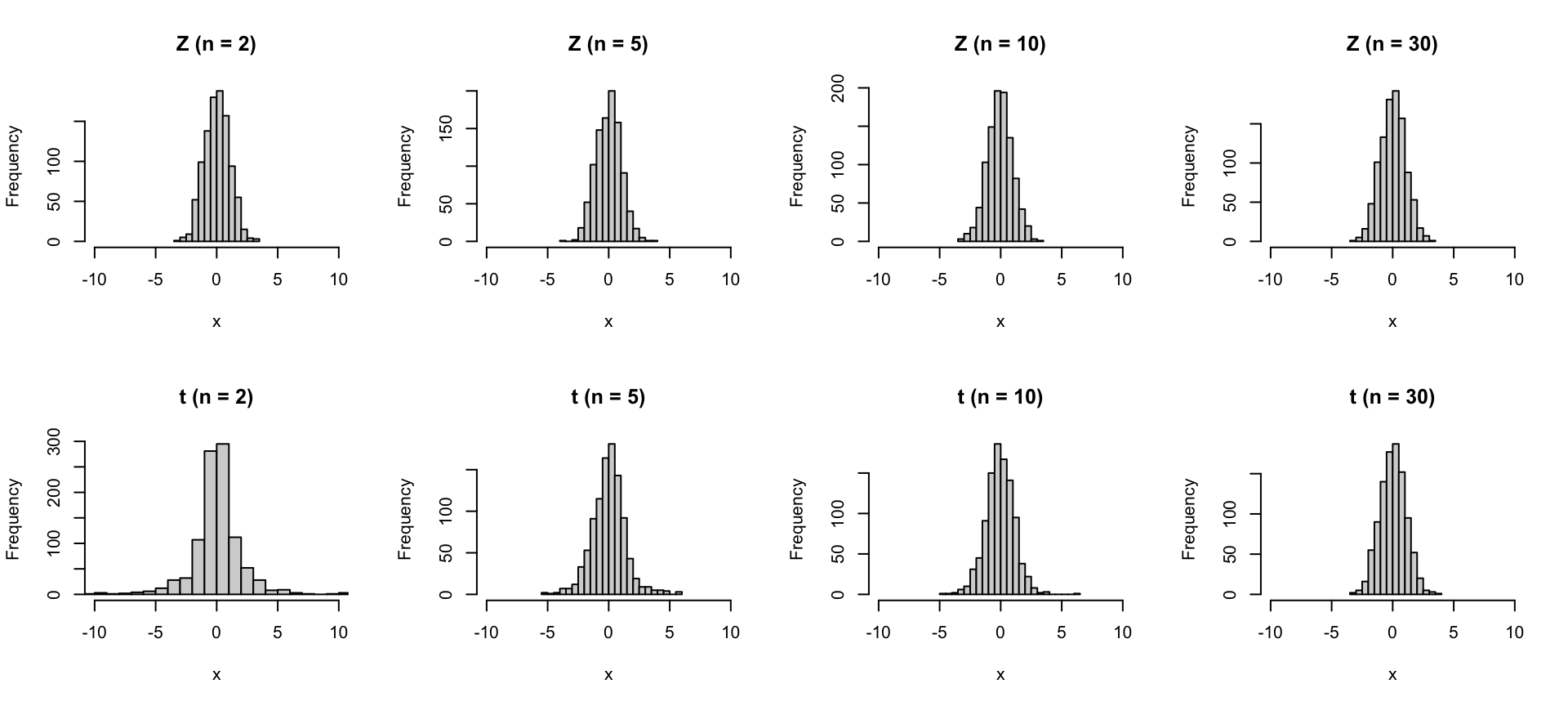
Chi-Quadrat-Verteilung
Eigenschaften
- Stetig, asymmetrisch und immer positiv.
- 1 Parameter (=Freiheitsgrad: n-1) der die Kurvenform bestimmt.
- Mittelwert = Anzahl an Freiheitsgraden (n-1), die Varianz = 2*(n-1)
- Verwendung bei
- Schätzung von Verteilungsparametern (z.B. Varianz)
- Beschreibung der Summe unabhängiger quadrierter standardnormalverteilter Zufallsvariablen
- Zum Testen
- der Unterschiede zwischen Grundgesamtheiten und Probenvarianzen
- zwischen theoretischen und beobachteten Verteilungen (\chi^2-Test als Anpassungstest)
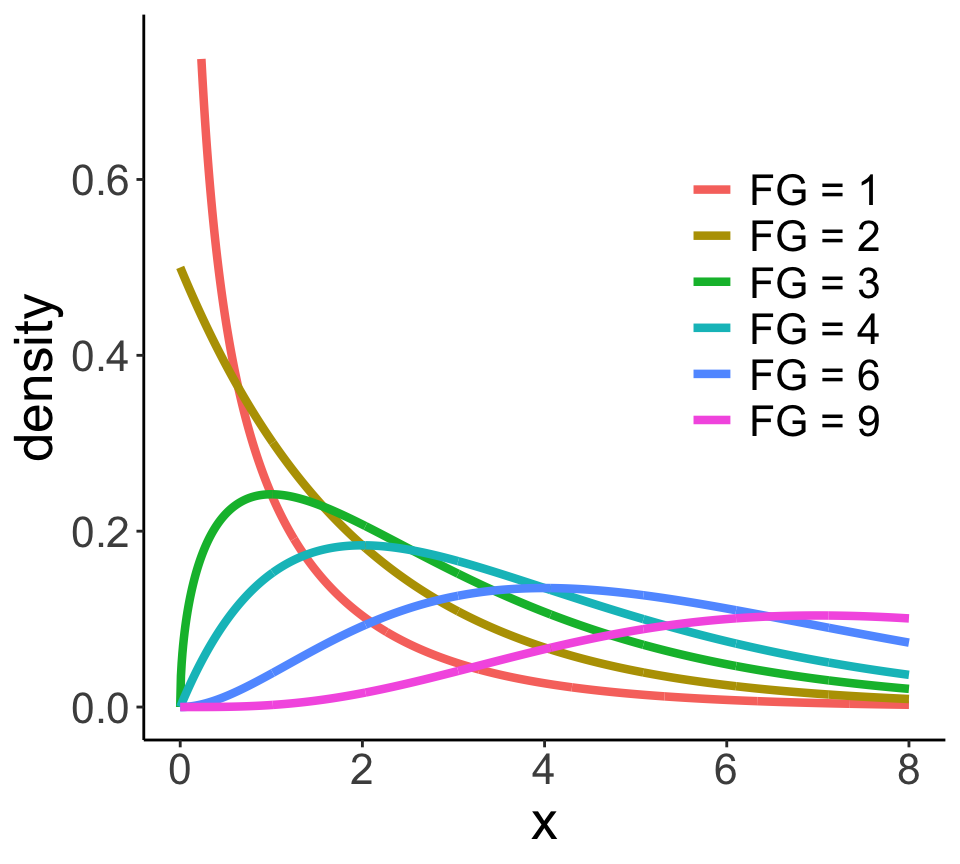
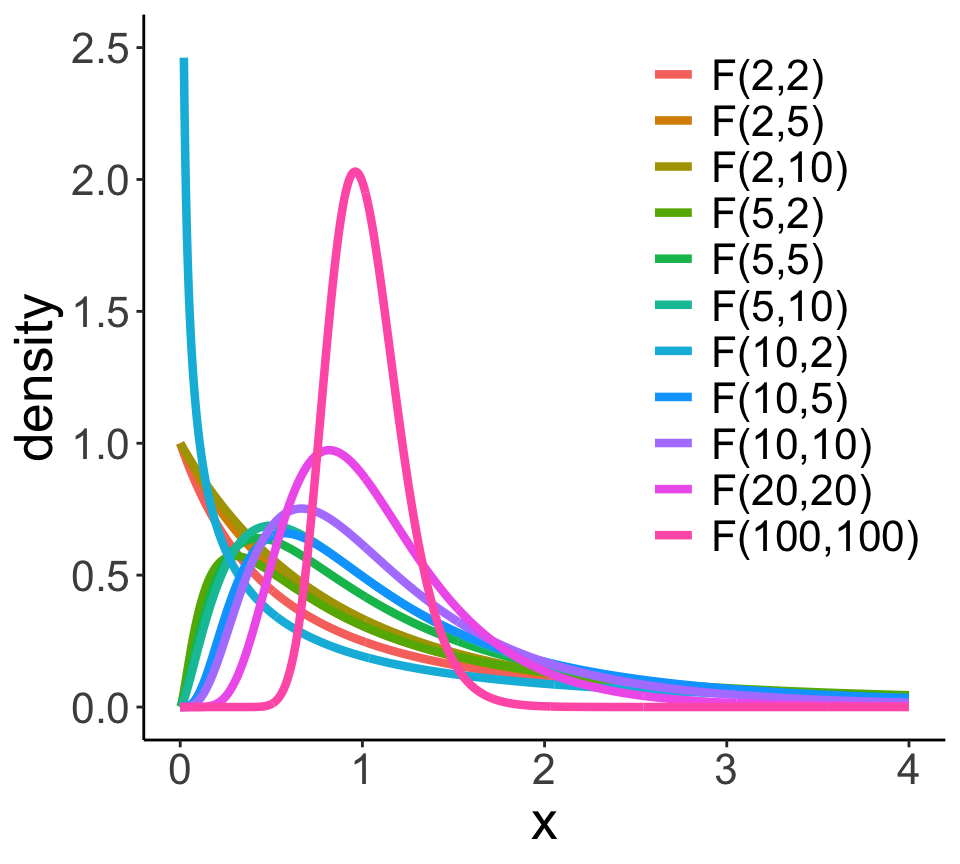
Fishers F-Verteilung
X ~ F(FG1, FG2)
- Verhältnis von zwei χ2-Verteilungen (z. B. zwei Varianzen)
- Wird zum Testen von Varianzverhältnissen in linearen Modellen verwendet.
- Besitzt 2 unabhängige Freiheitsgrade als Parameter
- Auch hier gilt, je nach Freiheitsgraden (d.h. Stichprobengröße) ist die Form der Kurve unterschiedlich.
Your turn …
![]()
03:00
Quiz 1 | Fragen
![]()
Nutzen Sie die Shiny App auf der nächsten Folie um folgende drei Fragen zu beantworten:
1. Normalverteilung
2. t-Verteilung
2. F-Verteilung
Quiz 1 | Shiny App
- Frage: P(X ≤ 14) bei N(29, 6.3)?
- Frage: P(-0.63 < X<1.78) bei t(7)?
- Frage: P(X > 2.22) bei F(41,15)?
Quiz 2 | Zum Ausprobieren in R
![]()
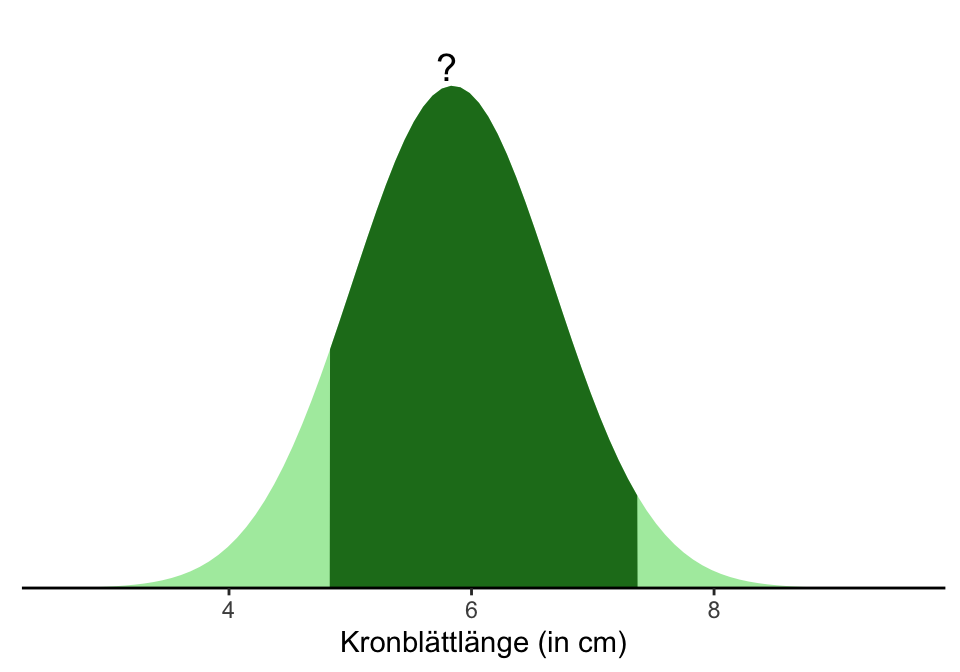
Wie hoch ist die Wahrscheinlichkeit, dass eine zufällig ausgewählte Blume aus dem iris Datensatz eine Kronblattlänge zwischen 4.8 und 7.4cm hat? Wir suchen also
P(4.8 < X \leq 7.4)= \int_{4.8}^{7.4} f_X(x)dx = P(X \leq 7.4) - P(X \leq 4.8)
Übungsaufgaben
![]()
Vorbereitungsaufgabe für Übungstag 2
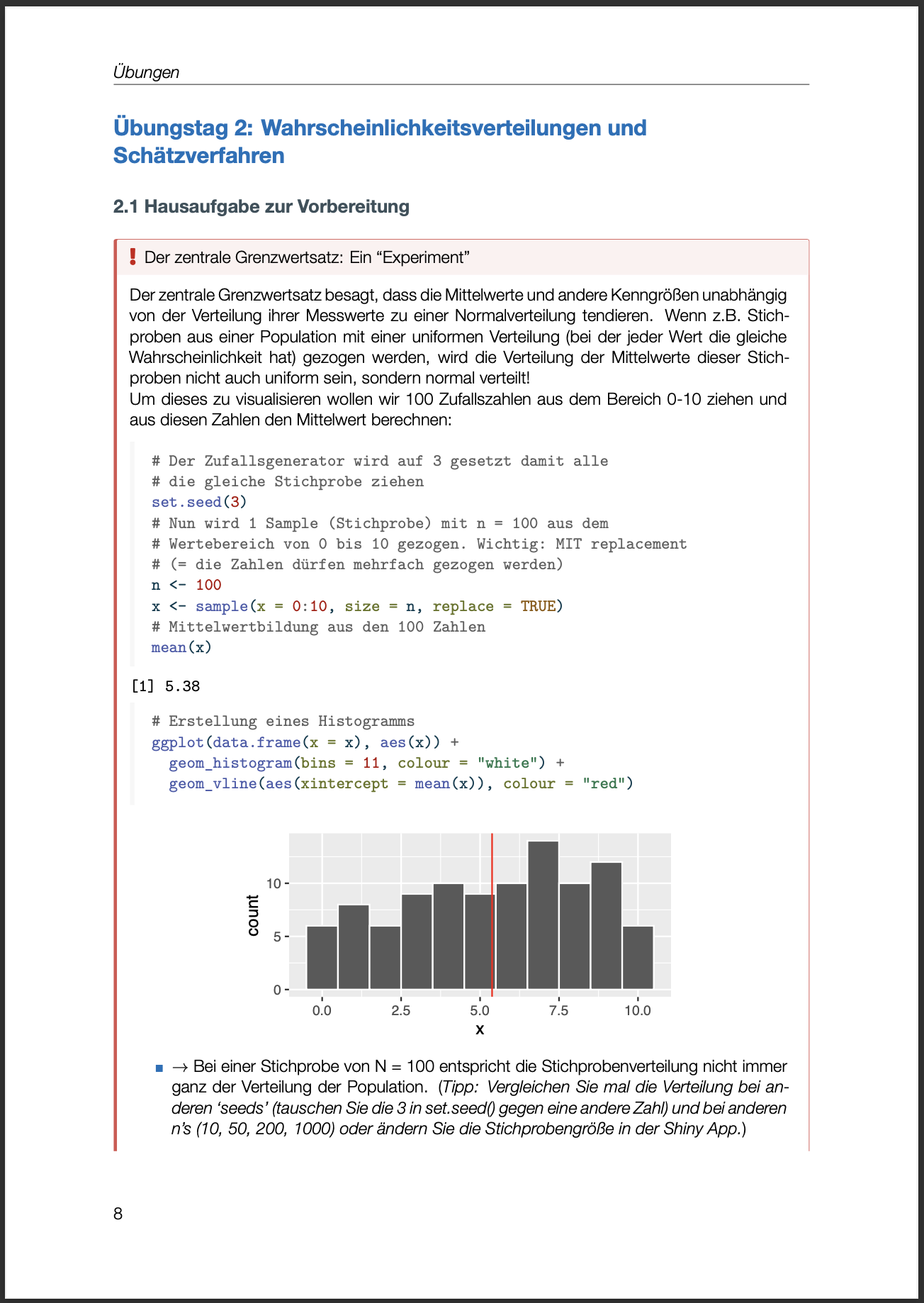
Was ist zu tun?
Eigene Simulationen zum zentralen Grenzwertsatz mithilfe der Shiny App durchführen → teaching-stats/clt/sample-means/
Wichtig
Moodle-Quiz VOR der nächsten Übung ausfüllen!
Fragen?
Abschlussquiz
![]()

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de

Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.
Kurswebseite: Data Science 2