2-Wahrscheinlichkeitstheorie

Data Science 2

Saskia Otto

Universität Hamburg, IMF

Sommersemester 2024

Lernziele

Nach Abschluss dieser VL und Übung werden Sie in der Lage sein..

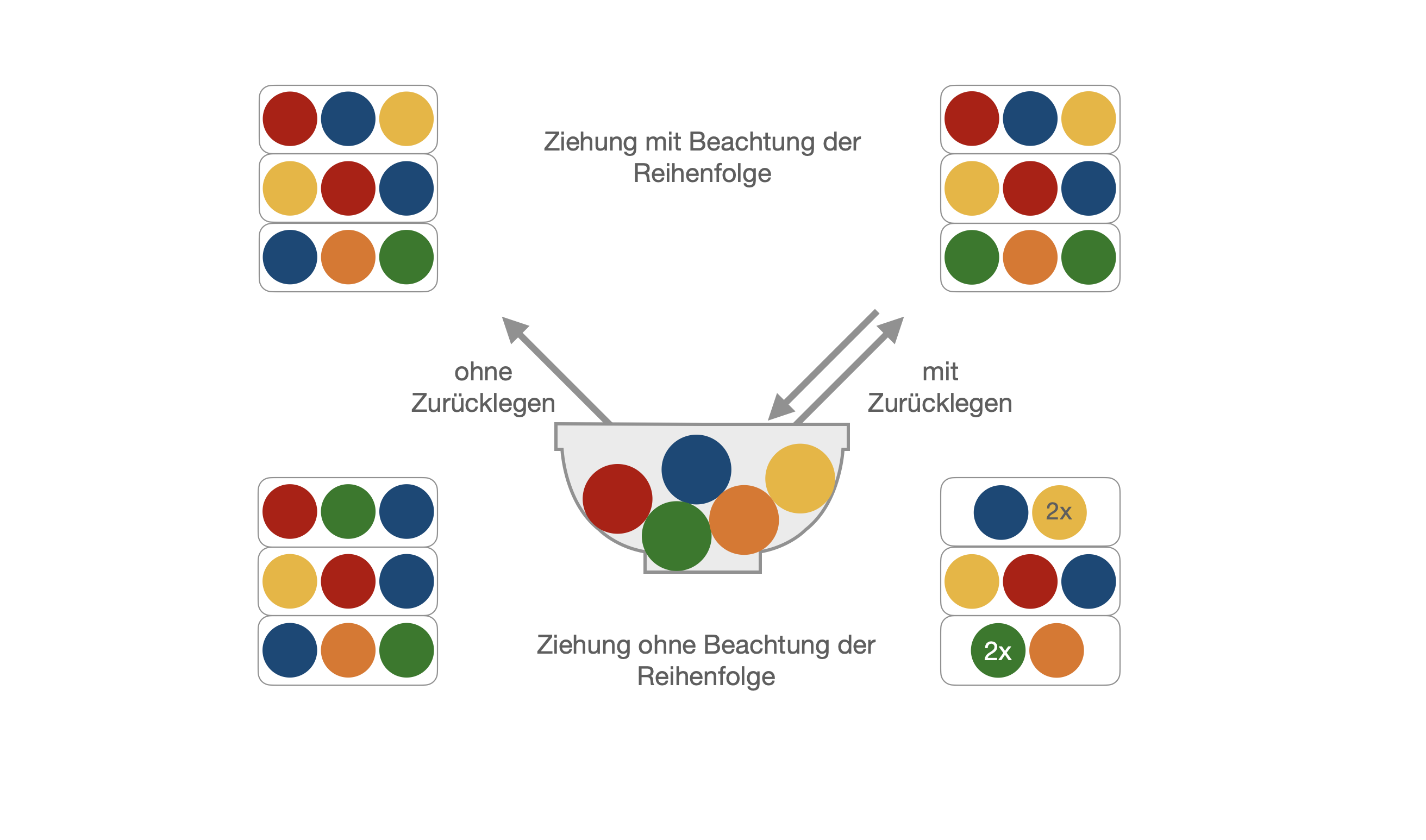
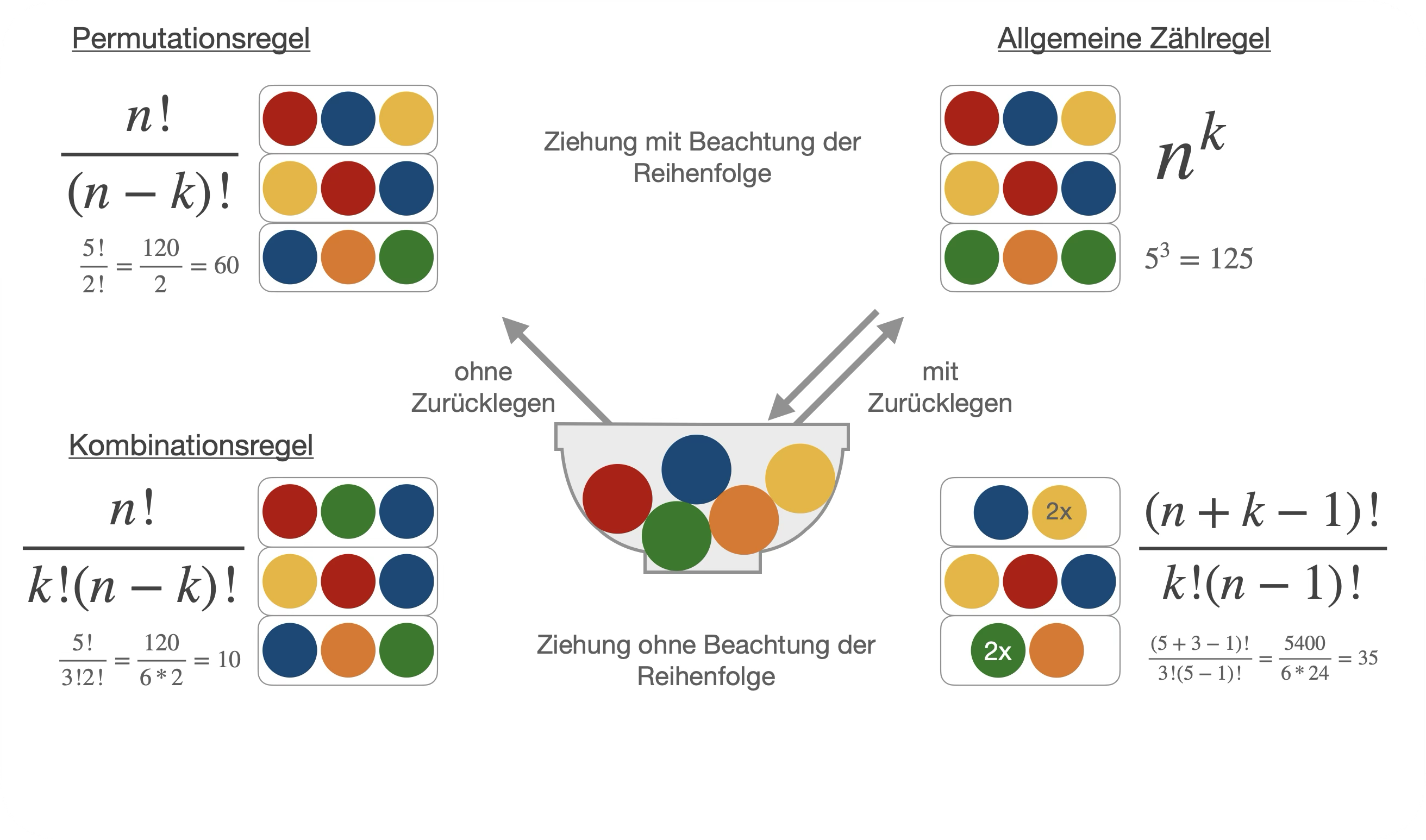
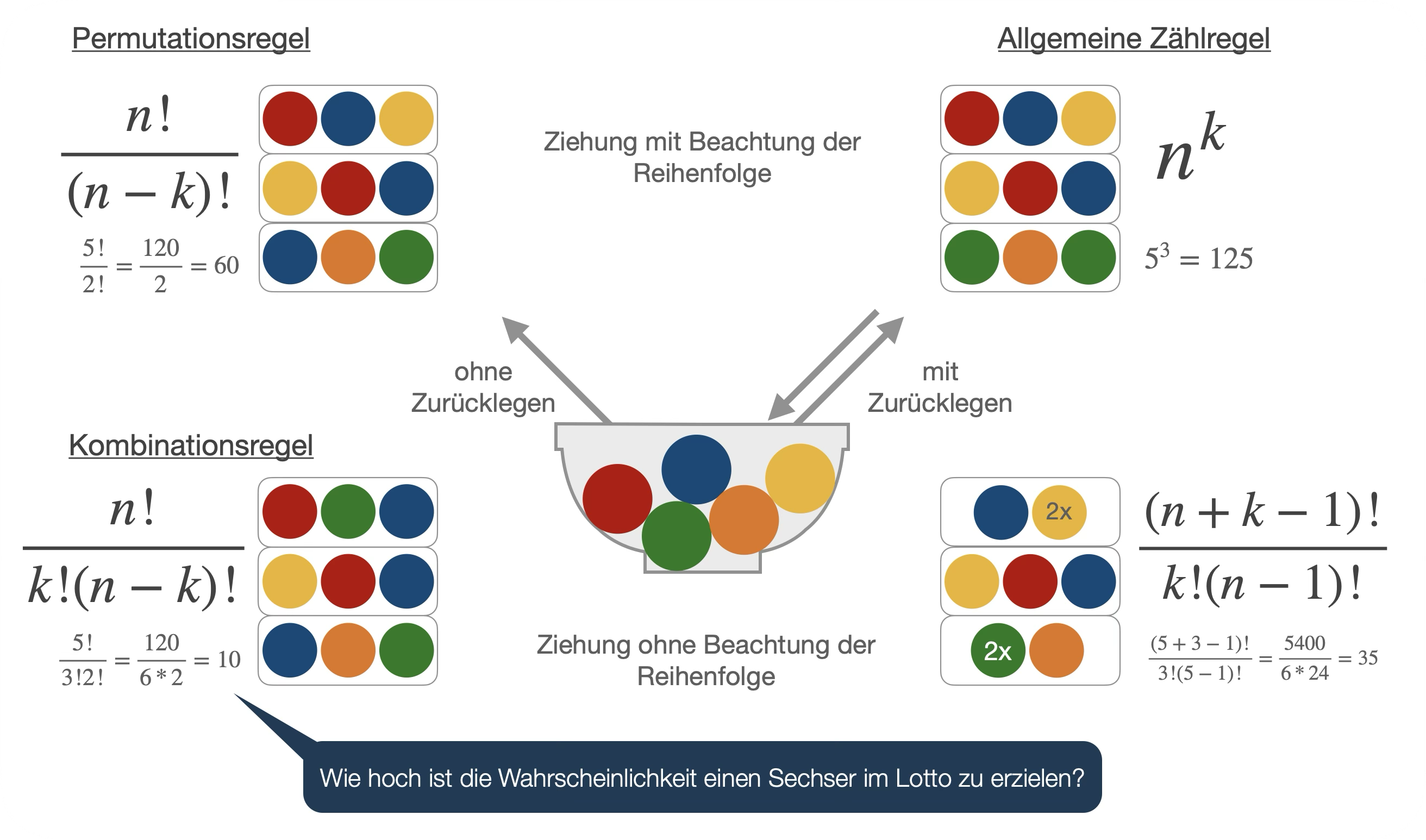
• Ergebnis- oder Stichprobenräume zu bestimmen (mittels Kombinatorik) zu bestimmen.
• die Wahrscheinlichkeit eines Ereignisses mit Hilfe der klassischen oder empirischen Wahrscheinlichkeitsrechnung zu ermitteln.
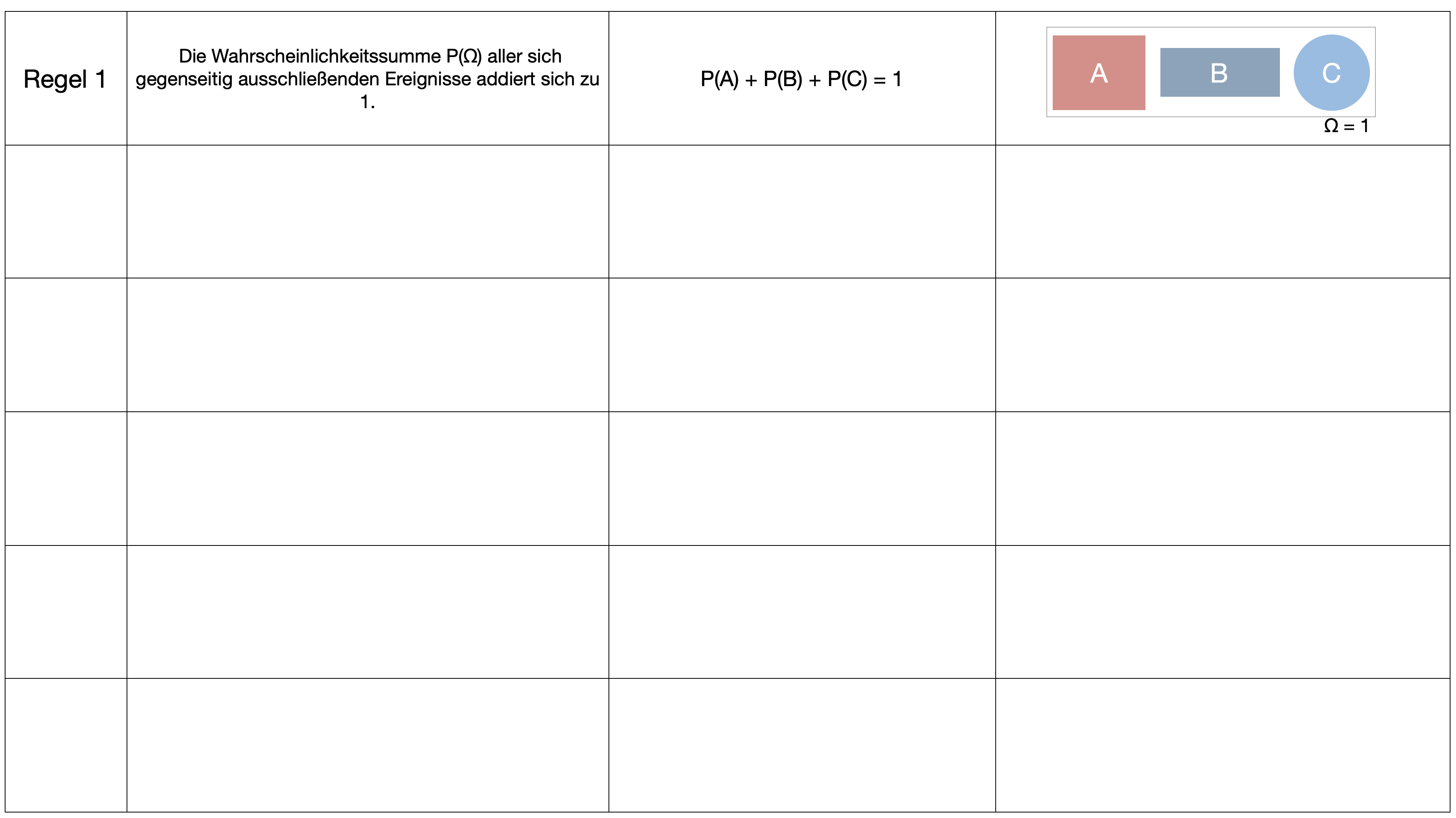
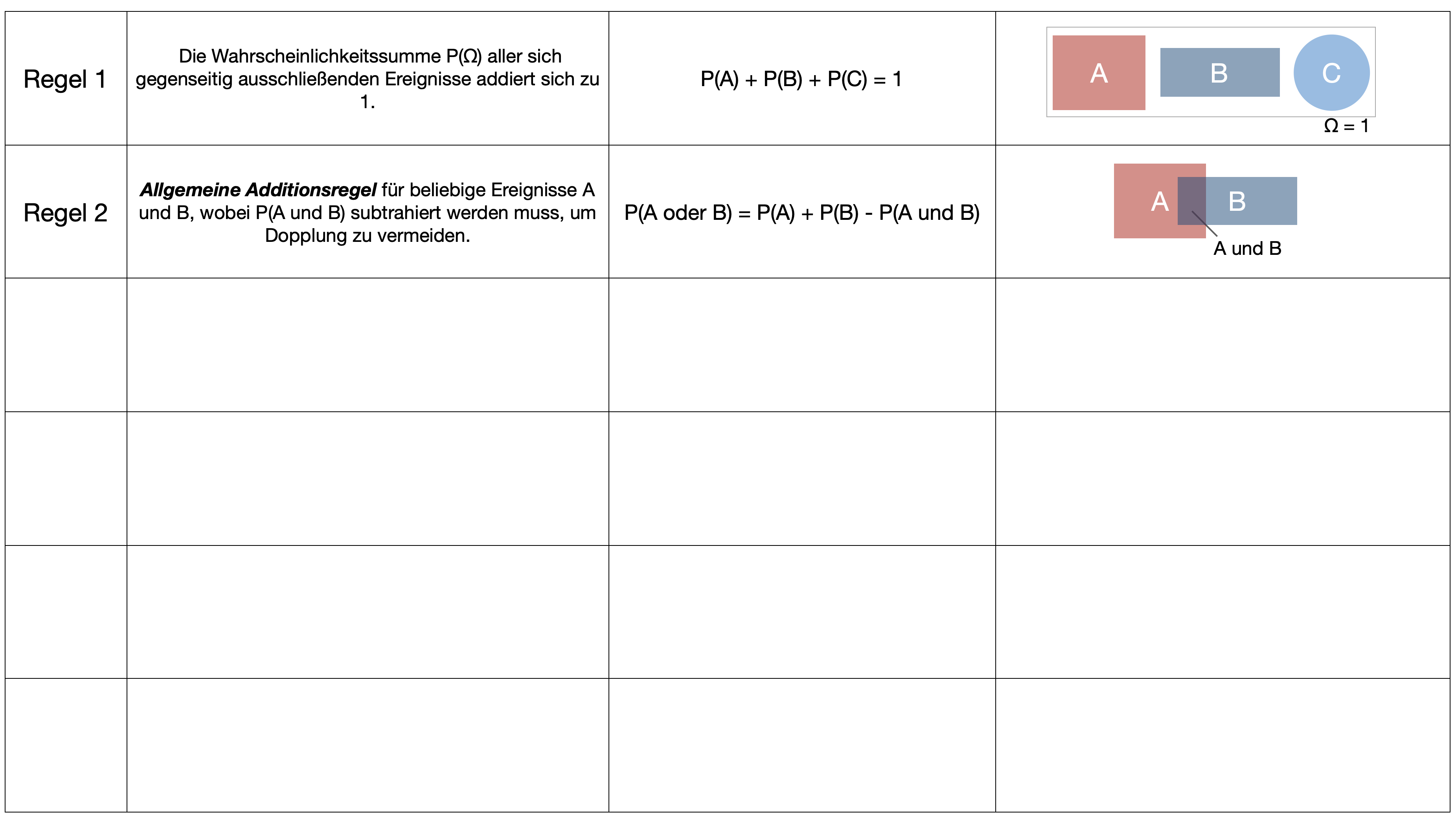
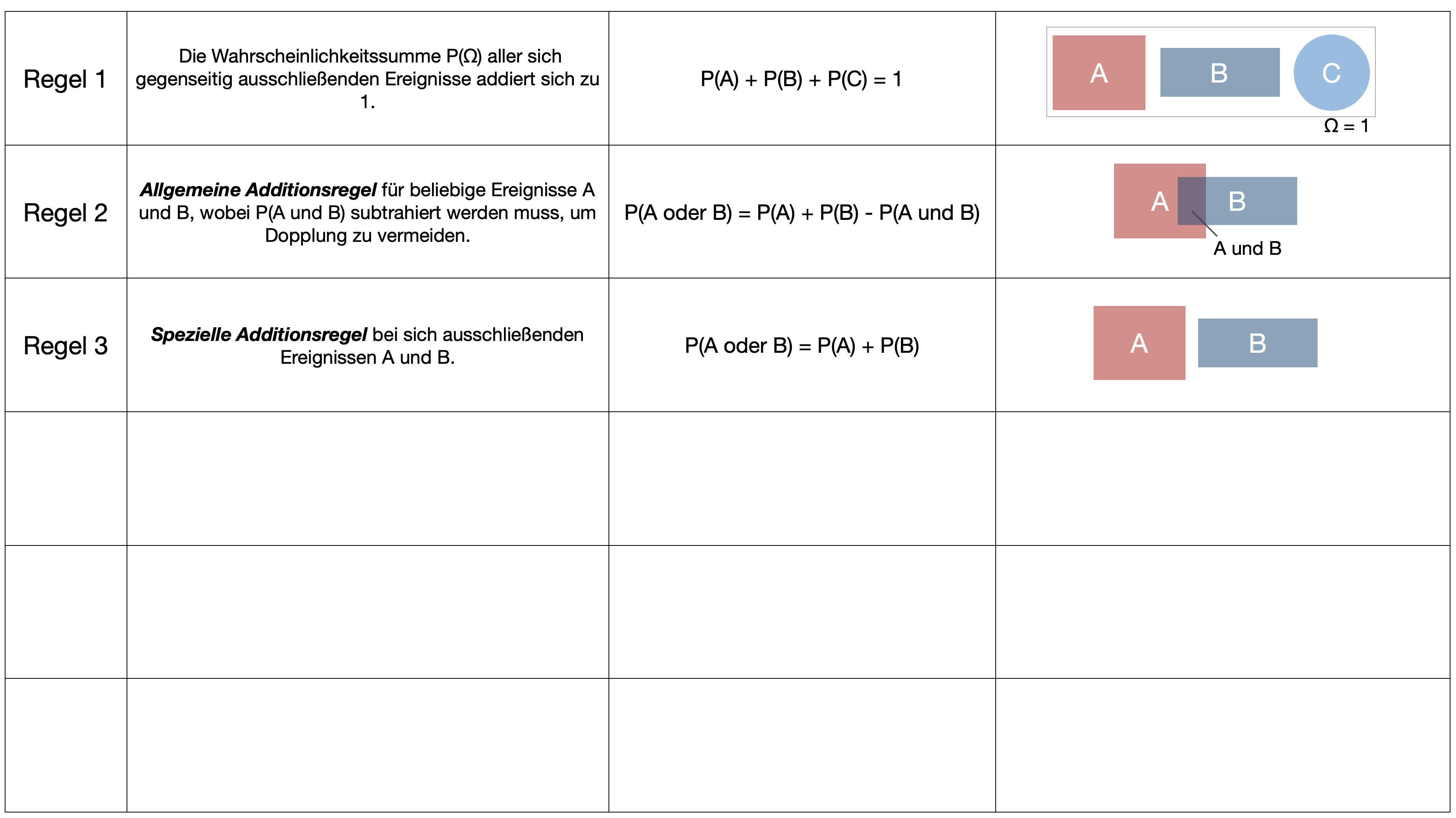
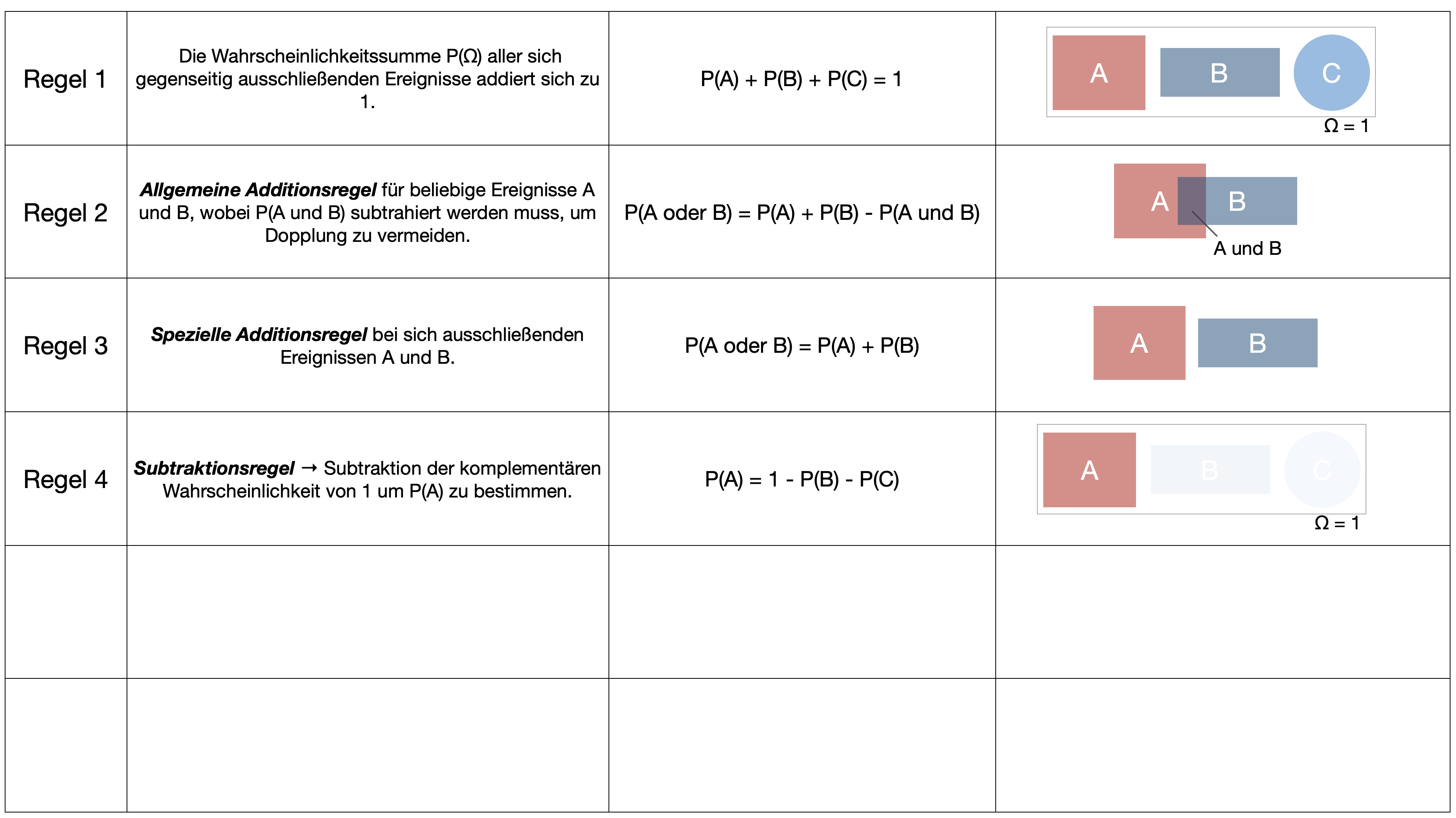
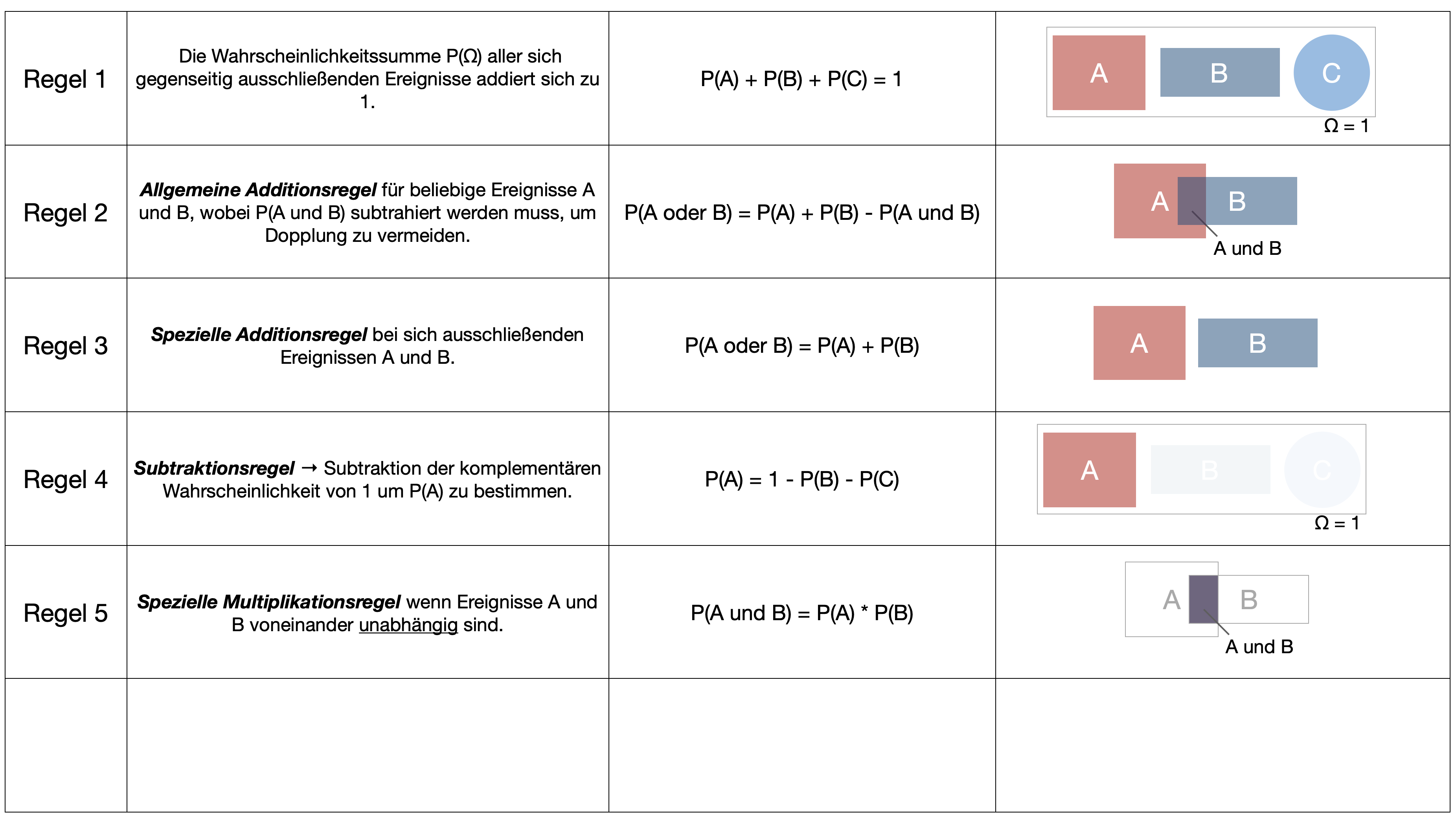
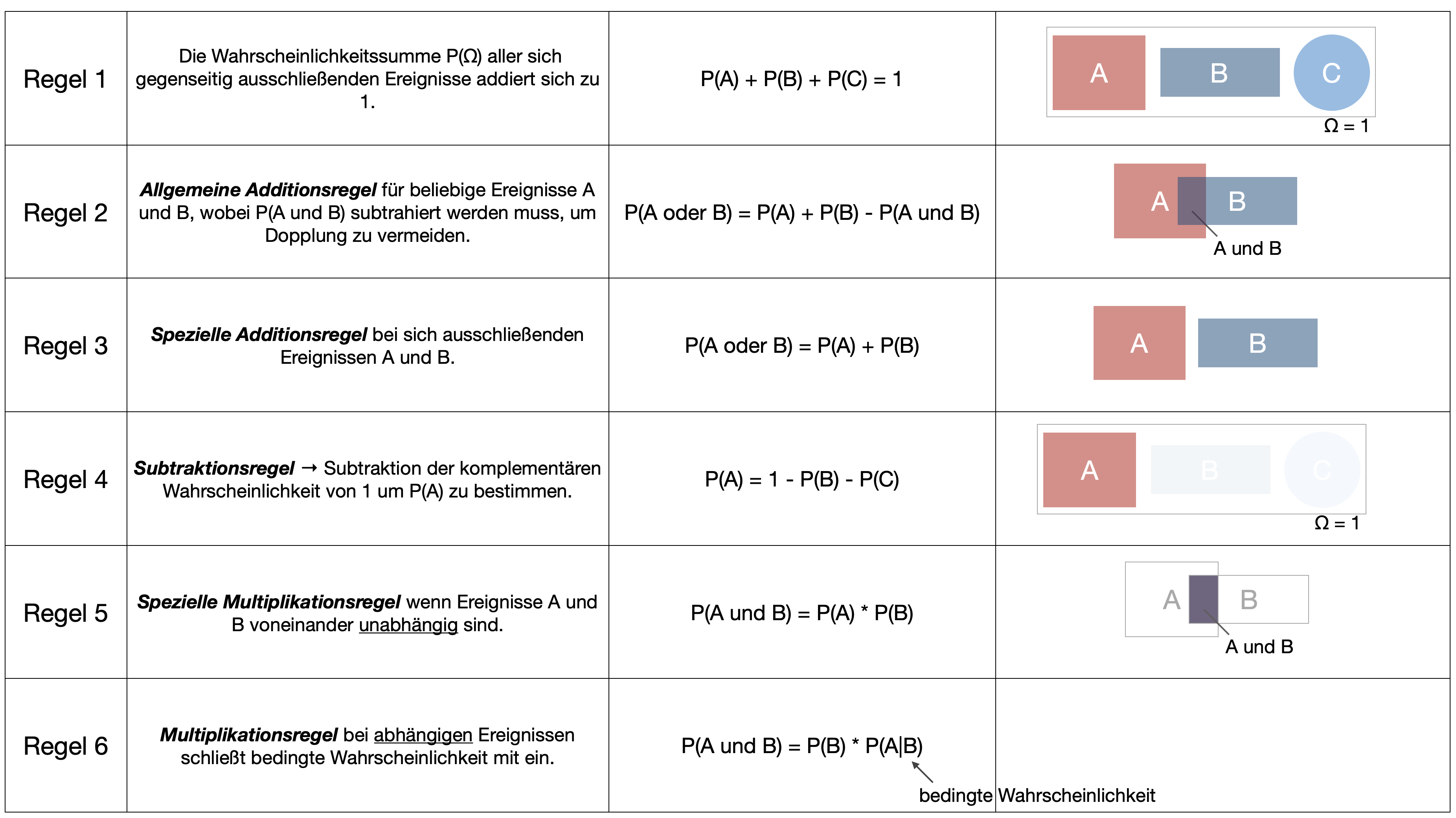
• Wahrscheinlichkeiten von zusammengesetzten Ereignissen unter Verwendung der Additions- und Multiplikationsregeln zu bestimmen.
• bedingte Wahrscheinlichkeiten eines Ereignisses zu bestimmen.
• die Sensitivität und Spezifität eines medizinischen Tests definieren zu können.

Ein paar Begriffe vorab

Begriff	Definition	Beispiel
Zufallsexperiment	Prozess, der zu genau definierten Ergebnissen (im Englischen ‘outcomes’) führt.	Würfelexperiment
Ergebnis \omega	Resultat oder Ausgang eines einzelnen Versuchs eines Zufallsexperiments bzw. Element der Ergebnismenge \Omega	Zufällig geworfene Augenzahl bei einem Würfel. Mögliche Ausgänge sind die Zahlen von 1 bis 6: \omega_{1}=1, \omega_{2}=2, .., \omega_{6}=6
Ergebnisraum/-menge \Omega	Gesamtheit aller möglichen Ergebnisse eines Zufallsexperiments mit der Wahrscheinlichkeit 1 (100%)	Beim Würfel ist \Omega = {1,2,3,4,5,6} → 6 mögliche Ergebnisse
Ereignis (Zufallsereignis)	Besteht aus einer Menge von Ergebnissen, dem eine Wahrscheinlichkeit zugeordnet werden kann. Ein Ereignis tritt ein, wenn es das Ergebnis des Zufallsexperiments als Element enthält.	Das Ereignis “eine gerade Zahl zu würfeln” ist die Teilmenge {2,4,6} aus der Ergebnismenge {1,2,3,4,5,6}

Kriterien eines Zufallsexperiment

• Alle möglichen Ausgänge sind vorab bekannt.
• Der einzelne Ausgang ist nicht vorhersehbar (Zufälligkeit).
• Der Zufallsversuch kann beliebig oft wiederholt werden.
• Ein Zufallsversuch muss immer unter gleichen Bedingungen wiederholt werden.
• Ein Zufallsversuch kann einstufig oder mehrstufig sein. Im zweiten Fall können die Stufen stochastisch unabhängig oder abhängig sein.
  • Einmaliges Ziehen einer Kugel aus einer Urne aus einem gemischten Stapel.
  • Ziehen mehrerer Kugeln aus einer Urne (mit oder ohne Zurücklegen)

Der Ergebnisraum | Beispiel 1

Bei 2 Würfeln enthält der Ergebnisraum 6 * 6 = 36 mögliche Ergebnisse (‘outcomes’).

Der Ergebnisraum | Beispiel 2

Wie viele Elemente enthält der Ergebnisraum für das Ziehen einer Karte aus einem gewöhnlichen Kartenspiel?

Bildquelle: www.pixabay.com

Ein kleiner Diskurs in die Kombinatorik..

Regeln der Kombinatorik

In vielen Fällen muss die Anzahl aller möglichen Ergebnisse für eine Folge von Ereignissen berechnet werden.

Beispiel: Münze & Würfel

Wie viele mögliche Ausgänge bzw. Ergebnisse gibt es, wenn zuerst eine Münze geworfen wird und dann der Würfel?

Beispiel 1: Münze & Würfel | Baumdiagramm

Zur Visualisierung von Ergebnisräumen

flowchart TD
 A[Zufallsexperiment]-- Münze --- B1[Kopf]
 A-- Münze --- B2[Zahl]
 B1-- Würfel --- C1[1]
 B1 --- C2[2]
 B1 --- C3[3]
 B1 --- C4[4]
 B1 --- C5[5]
 B1 --- C6[6]
 B2-- Würfel ---  C7[1]
 B2 --- C8[2]
 B2 --- C9[3]
 B2 --- C10[4]
 B2 --- C11[5]
 B2 --- C12[6]
 C1 -- Ergebnis --- D1(K,1):::e
 C2 --- D2(K,2):::e
 C3 --- D3(K,3):::e
 C4 --- D4(K,4):::e
 C5 --- D5(K,5):::e
 C6 --- D6(K,6):::e
 C7 --- D7(M,1):::e
 C8 --- D8(M,2):::e
 C9 --- D9(M,2):::e
 C10 --- D10(M,2):::e
 C11 --- D11(M,2):::e
 C12 --- D12(M,2):::e
 classDef e fill:#0271BB

Beispiel 1: Münze & Würfel | Regel

• Anzahl an Ausgängen Münze: k_1 = 2
• Anzahl an Ausgängen Würfel: k_2 = 6

Grundlegende Zählregel

Werden n voneinander unabhängige (ev. verschiedene) Zufallsexperimente durchgeführt und besteht das erste Experiment aus k_1 möglichen Ergebnissen, das zweite aus k_2, dann sind k_1*k_2*...*k_n die möglichen verschiedenen Ergebnisvariationen.

➜ Es gibt entsprechend 2*6 = 12 mögliche Ausgänge.

Das Urnenmodell

4 Typen eines mehrstufigen Experiments

Beispiel 2: 4-stellige Proben-ID

• In einem Experiment sollen 4-stellige IDs für die Proben vergeben werden.
• Wie viele verschiedene IDs können vergeben werden, wenn nur die Ziffern 1 bis 6 verwendet werden (mit und ohne Wiederholung, Reihenfolge ist relevant)?

Mit Wiederholung/Zurücklegen

• n = 6 (1,2,3,4,5,6)
• k = 4
• 6*6*6*6 = 6^4 = 1296

→ Allgemeine Zählregel

Ohne Wiederholung/Zurücklegen

• Ziffer 1 hat 6 Möglichkeiten,
• Ziffer 2 nur noch 5,
• Ziffer 3 hat 4 und
• Ziffer 4 nur noch 3 Möglichkeiten.
• 6*5*4*3 = 360 bzw. \frac{n!}{(n-k)!} = \frac{6!}{(6-4)!}=\frac{720}{2} = 360

→ Permutationsregel

Wenn die Reihenfolge keine Rolle spielt…

Die Kombinationsregel

Wie viele verschiedene Möglichkeiten hat ein Forscher, aus 10 Ratten 5 Ratten auszuwählen und jede einem anderen Test zu unterziehen?

Ziehung ohne Zurücklegen und OHNE Beachtung der Reihenfolge

Wählt man aus n verschiedenen Objekten k zufällig aus und lässt man hierbei die Reihenfolge außer acht, ergeben sich für k Objekte \frac{n!}{k!(n-k)!} mögliche Kombinationen:

\frac{10!}{5!(10-5)!} = \frac{3628800}{120*120} = 252

Wenn die Reihenfolge eine Rolle spielt…

Permutationssregel

• In einer Studie soll ein Landschaftsschutzgebiet (LSG) im Frühjahr, ein anderes im Herbst untersucht werden. Beide LSG werden aus einer Gruppe von insgesamt 9 LSG (A-I) zufällig ausgewählt.
• Wie viele Permutationen sind möglich und wie groß ist die Wahrscheinlichkeit, dass LSG F im Frühjahr und H im Herbst beprobt wird?

Ziehung ohne Zurücklegen und MIT Beachtung der Reihenfolge

Bei Berücksichtigung der Reihenfolge ergeben sich für k=2 Objekte (aus n=9):

\frac{n!}{(n-k)!} = \frac{9!}{(9-2)!} = \frac{362880}{5040} = 72

Entsprechend ist die Wahrscheinlichkeit: P(F,H) = \frac{1}{72}

Bildquelle: Wikipedia(CO 1.0 Lizenz)

..zurück zur Wahrscheinlichkeit

Wie wird Wahrscheinlichkeit definiert?

Drei grundlegende Interpretationen der Wahrscheinlichkeit:

1. Klassische Wahrscheinlichkeit
2. Empirische oder relative Häufigkeitswahrscheinlichkeit
3. Subjektive Wahrscheinlichkeit

Klassischer Ansatz (LaPlace, Bernoulli)

• aus dem Glücksspiel entwickelt (17./18. Jhd.)
• verwendet Ergebnisräume um Wahrscheinlichkeiten zu bestimmen, dass ein Ereignis eintritt
• braucht kein Experiment
• Ein einzelner Versuch hat endlich viele, gleich wahrscheinliche Ausgänge (der ideale Würfel).

Formel der klassischen Wahrscheinlichkeit

Die Wahrscheinlichkeit eines Ereignis E ist

P(E) = \frac{n(E)}{n(\Omega)} = \frac{\text{Anzahl der Ergebnisse in E}}{\text{Gesamtzahl der Ergebnisse im Ergebnisraum}}

Anwendungsbeispiel 1: Das Problem von Galilei

Wie groß sind die Wahrscheinlichkeiten, mit 3 Würfeln eine Summe von 9 oder 10 zu erhalten?

• Der Ergebnisraum umfasst insgesamt 216 Ergebnisse (6^3= 216)
• Wie viele Ergebnisse ergeben in der Summe 9 bzw. 10?

Das Problem von Galilei | Summe 9

25 Ergebnisse ergeben in der Summe 9:

Das Problem von Galilei | Summe 10

27 Ergebnisse ergeben in der Summe 10:

Das Problem von Galilei | Theoretischer Ansatz

Wie groß sind die Wahrscheinlichkeiten, mit 3 Würfeln eine Summe von 9 oder 10 zu erhalten?

• Der Ergebnisraum umfasst insgesamt 216 Ergebnisse (6 * 6 * 6 = 216)
• Wie viele Ergebnisse ergeben in der Summe 9 bzw. 10? 25 bzw. 27

Berechnung

P(\text{Summe 9}) = \frac{n(E)}{n(\Omega)} = \frac{25}{216} = 0.1157

P(\text{Summe 10}) = \frac{n(E)}{n(\Omega)} = \frac{27}{216} = 0.1250

Empirische Wahrscheinlichkeit

• Beruht auf der gemessenen Häufigkeit eines bestimmten Ereignisses → relative Häufigkeitswahrscheinlichkeit
• Grundlage der frequentistischen Statistik
• P entspricht dem Grenzwert der relativen Häufigkeiten des Auftretens des Ereignisses

Formel der empirischen Wahrscheinlichkeit

P(E) = lim(rel.Häufigkeit)=\frac{lim(Anzahl~Ereignis)}{Stichprobenzahl}

Das Problem von Galilei | Empirischer Ansatz

Theoretische Werte: P(Summe 9) = 0.1157 und P(Summe 10) = 0.1250

Funktion

calc_prob <- function(n = 100) {
  # Erstellung leerer Vektoren
  true9<- vector("logical", n)
  true10 <- vector("logical", n)
  # Schleife
  for (i in 1:n) {
    # '3-maliges Würfel'
    sum3 <- sum(sample(1:6,3,replace = T))
    # Ist die Summe 9 oder 10?
    true9[i] <- ifelse(sum3 == 9, T, F)
    true10[i] <- ifelse(sum3 == 10, T, F)
  }
  # Ausgabevektor: Anzahl Summe 9 bzw. 10
  out <- c(
    prob9 = round(sum(true9)/n, 4), 
    prob10 = round(sum(true10)/n, 4)
  )
  return(out)
}

Simulation

calc_prob(n = 20)

 prob9 prob10 
  0.00   0.35 

calc_prob(n = 20)

 prob9 prob10 
   0.1    0.2 

calc_prob(n = 20)

 prob9 prob10 
  0.00   0.05 

calc_prob(n = 100)

 prob9 prob10 
  0.18   0.07 

calc_prob(n = 100)

 prob9 prob10 
  0.10   0.11 

calc_prob(n = 100000)

 prob9 prob10 
 0.116  0.125 

calc_prob(n = 100000)

 prob9 prob10 
 0.116  0.124 

Subjektivistische Wahrscheinlichkeitsauffassung

Bayes’scher Wahrscheinlichkeitsbegriff

• Basiert auf einer fundierten Vermutung oder Schätzung, wobei Meinungen und unvorhergesehene Informationen verwendet werden.
• Bei einmaligen Zufallsereignissen kann man deren Eintrittswahrscheinlichkeit nur schätzen, nicht berechnen.
• Spielt v.a. im Alltag eine große Rolle.
• Darf nicht mit dem gleichfalls auf Thomas Bayes zurückgehenden Satz von Bayes verwechselt werden.

Bildquelle: https://mostlybrightideas.wordpress.com/2013/05/06/probable-cause-part-1/

Regeln der Wahrscheinlichkeitsrechnung

Anwendungsbeispiel 2: De-Méré-Paradoxon

Was ist wahrscheinlicher, in vier Würfen eines einzelnen Würfels mindestens eine ‘6’ zu würfeln (Variante A) ODER in 24 Würfen eines Würfelpaars mindestens eine ‘Doppelsechs’ zu erzielen (Variante B)?

→ Anwendung der speziellen Multiplikationsregel (Regel 5) und der Subtraktionsregel (Regel 4):

Variante A

P(\text{viermal nicht 6}) = \frac{5}{6}*\frac{5}{6}*\frac{5}{6}*\frac{5}{6} = 0.482

P(\text{mindestens eine 6}) = 1 - 0.482 = 0.518

Variante B

P(\text{keine Doppelsechs in 24 Würfen}) = (\frac{35}{36})^{24} = 0.509

P(\text{mindestens eine Doppelsechs}) = 1 - 0.509 = 0.491

De-Méré-Paradoxon | Empirischer Ansatz 1

Funktion

calc_prob2 <- function(n = 100) {
  successA <- vector("logical", n)   # Variante A
  for (i in 1:n) {
    rdraw <- sample(1:6, 4, replace = TRUE)
    successA[i] <- ifelse(6 %in% rdraw, TRUE, FALSE)
  }
  probsA <- round(sum(successA)/n, 4)
  successB <- vector("logical", n)  # Variante B
  for (i in 1:n) {
    ind_success <- vector("logical", 24)
    for (j in 1:24) {
      rdraw <- sample(1:6, 2, replace = TRUE)
      ind_success[j] <- ifelse(all(rdraw == c(6,6)), TRUE, FALSE)
    }
    successB[i] <- any(ind_success)
  }  
  probsB <- round(sum(successB)/n, 4)
  out <- c(probsA = probsA, probsB = probsB)   # Ausgabe
  return(out)
}

De-Méré-Paradoxon | Empirischer Ansatz 2

Theoretische Werte: P(Variante A) = 0.518 und P(Variante B) = 0.491

Simulation

calc_prob2(n = 20)

probsA probsB 
  0.55   0.60 

calc_prob2(n = 20)

probsA probsB 
  0.65   0.65 

calc_prob2(n = 20)

probsA probsB 
  0.30   0.35 

calc_prob2(n = 100)

probsA probsB 
  0.61   0.61 

calc_prob2(n = 100)

probsA probsB 
  0.48   0.46 

calc_prob2(n = 100000)

probsA probsB 
 0.517  0.493 

calc_prob2(n = 100000)

probsA probsB 
 0.520  0.492 

Bedingte Wahrscheinlichkeit & Satz von Bayes

Bedingte Wahrscheinlichkeit

Die bedingte Wahrscheinlichkeit eines Ereignisses B ist die Wahrscheinlichkeit, dass B eintreten wird, vorausgesetzt, dass A bereits eingetreten ist.

Was könnten mögliche Fragestellungen sein?

Bedingte Wahrscheinlichkeit | Beispiele

Wie groß ist die Wahrscheinlichkeit, dass ..

• ein Individuum auf einem Bild wirklich zu Art A gehört, wenn die automatisierte Bildklassifizierung es dorthin einordnet?
• eine Frau bei einem positiven Schwangerschaftstest tatsächlich schwanger ist?
• ein/e Student/in in einem Masterprogramm aufgenommen wird UND ein Zimmer im Studentenwohnheim bekommt?

Wir brauchen die Bayessche Formel

Anwendungsbeispiel: Medizinische Diagnostik

Die Wirksamkeit des Corona Schnelltests:

Wie hoch ist die Wahrscheinlichkeit, dass eine getestete Person bei einem positiven Coronavirus-Schnelltest tatsächlich infiziert ist?

→ gesucht wird P(A|B), also P(infiziert|positiv)

Angenommen

• Prävalenz ist 0.05% (5 von 10000 Einwohner sind infiziert)
• Sensitivität ist 80%
• Spezifität ist 98%

Bildquelle: de.freepik.com

Medizinische Diagnostik | Begriffe

Vorab ein paar Begriffserklärungen

• Prävalenz: Häufigkeit einer Infektion, Krankheit oder eines Symptoms in einer Population zu einem bestimmten Zeitpunkt. → P(infiziert) bzw. P(A)
• Sensitivität: Anteil richtig positiver Ergebnisse, wenn die Untersuchten tatsächlich infiziert sind. → In unserem Beispiel P(positiv|infiziert) bzw. P(B|A)
• Spezifität: Anteil der richtig negativen Testergebnissen unter allen gesunden Untersuchten. → In unserem Beispiel P(negativ|nicht\:infiziert) bzw. P(nB|nA)

Medizinische Diagnostik | Bayes

Medizinische Diagnostik | Berechnung

\begin{align} P(A|B) &= \frac{P(A)*P(B|A)}{P(B)}\\ &=\frac{P(A)*P(B|A)}{P(A)*P(B|A)+P(nA)*P(B|nA)}\\ &=\frac{0.0005*0.8}{0.0005*0.8+0.9995*0.02}\\ &=\frac{0.0004}{0.0204} = 0.0196 \end{align}

→ Die Wahrscheinlichkeit, dass eine getestete Person bei einem positiven Testergebnis tatsächlich infiziert ist, liegt bei NUR 1.96 %, wenn die Prävalenz 0.05 % beträgt!!!!

Herleitung mit der Kreuztabelle

Der Satz von Bayes

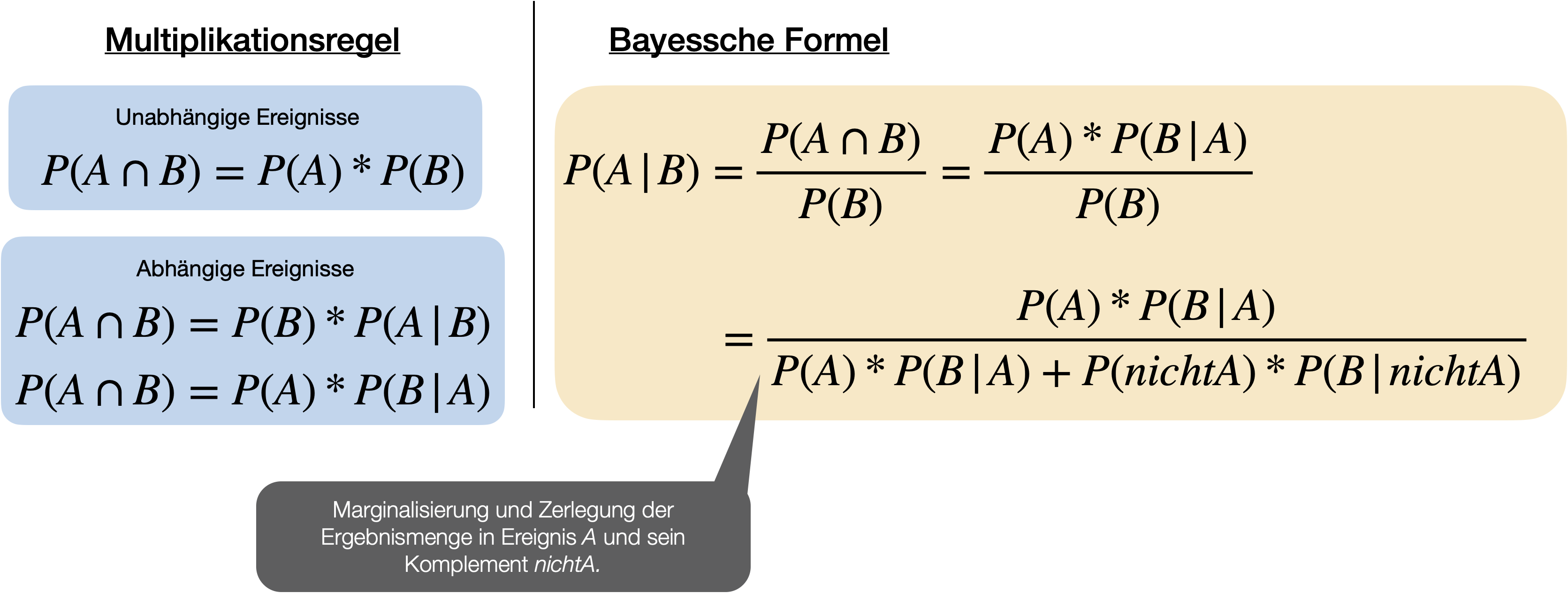
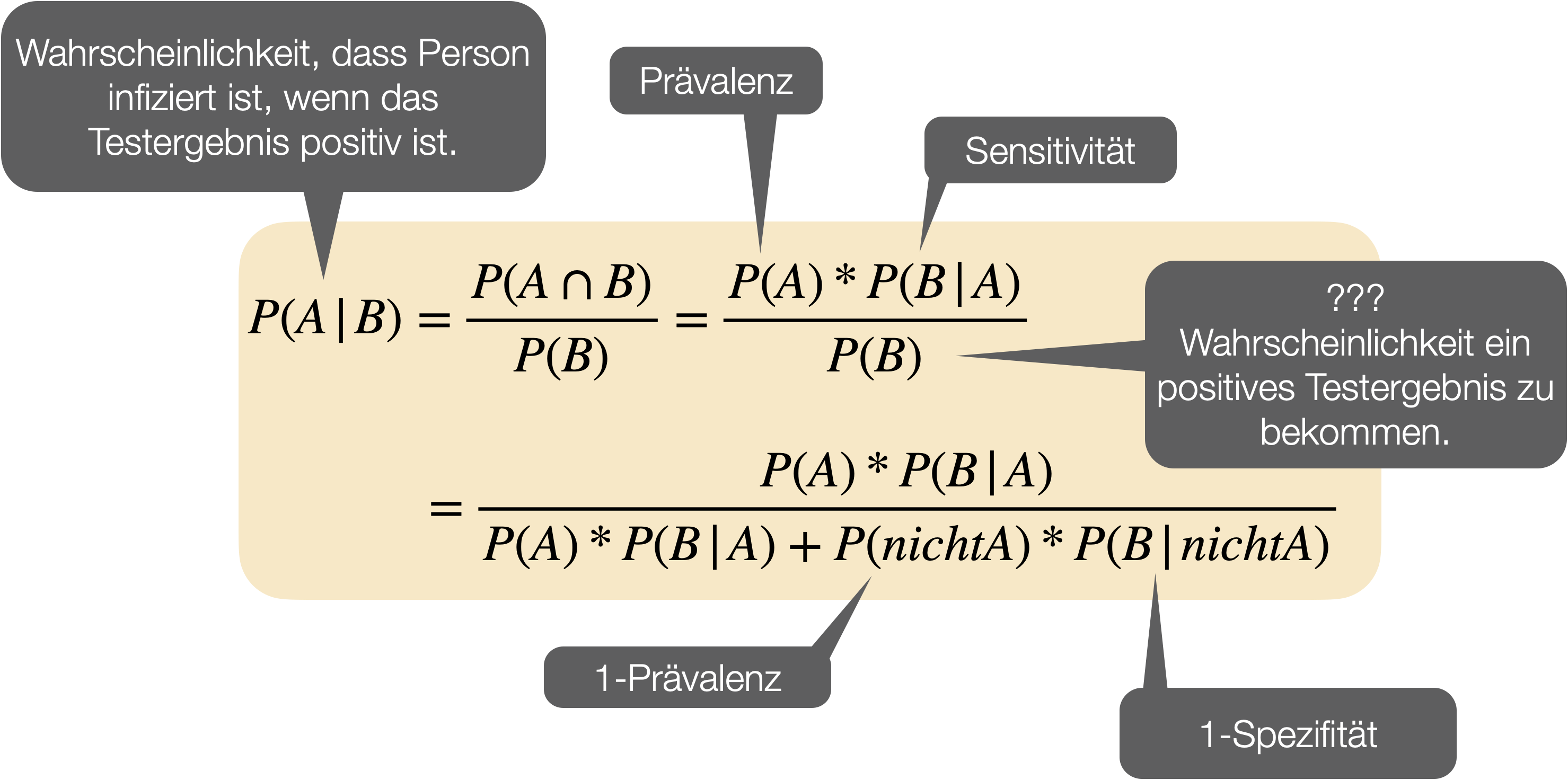
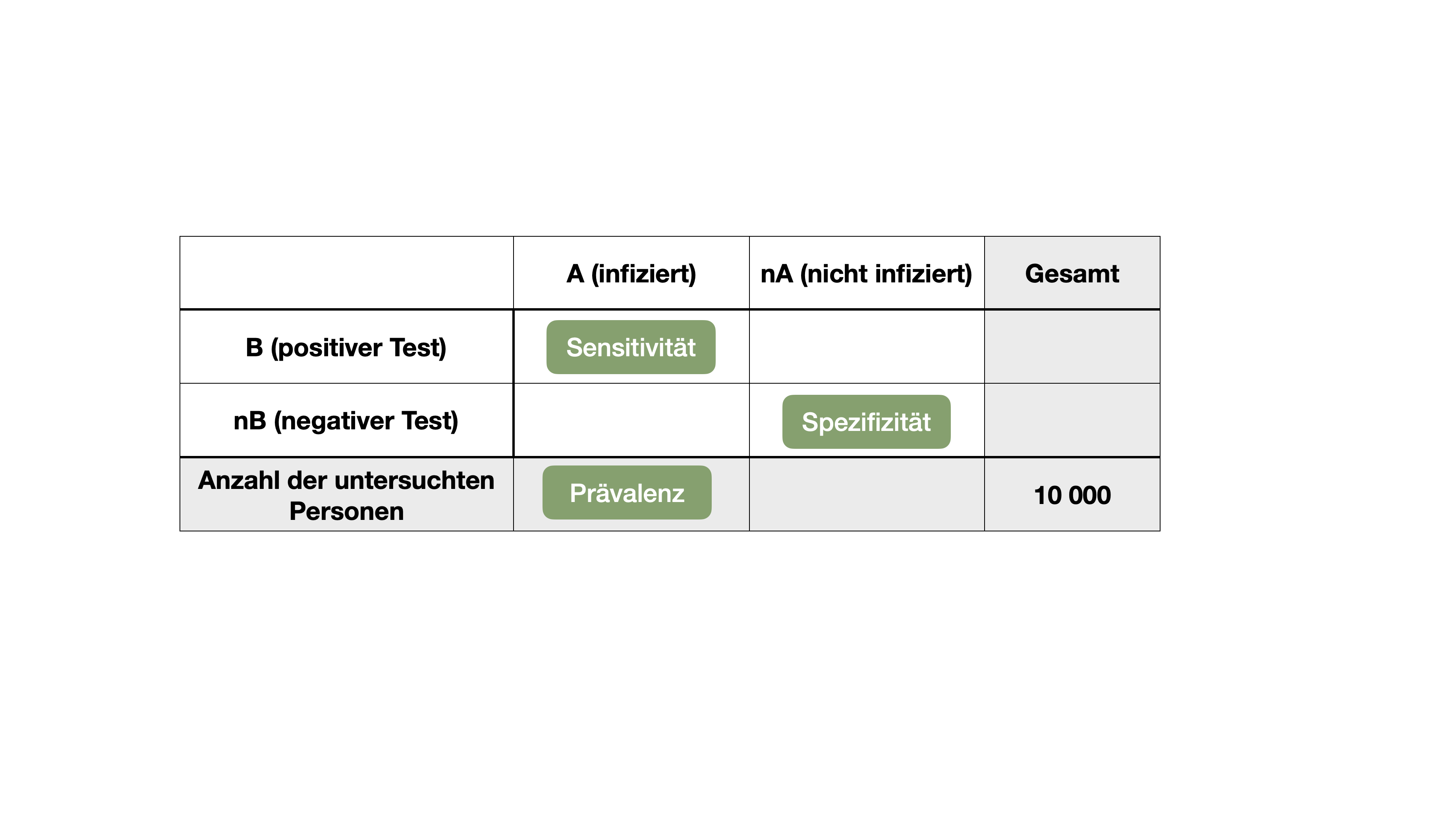
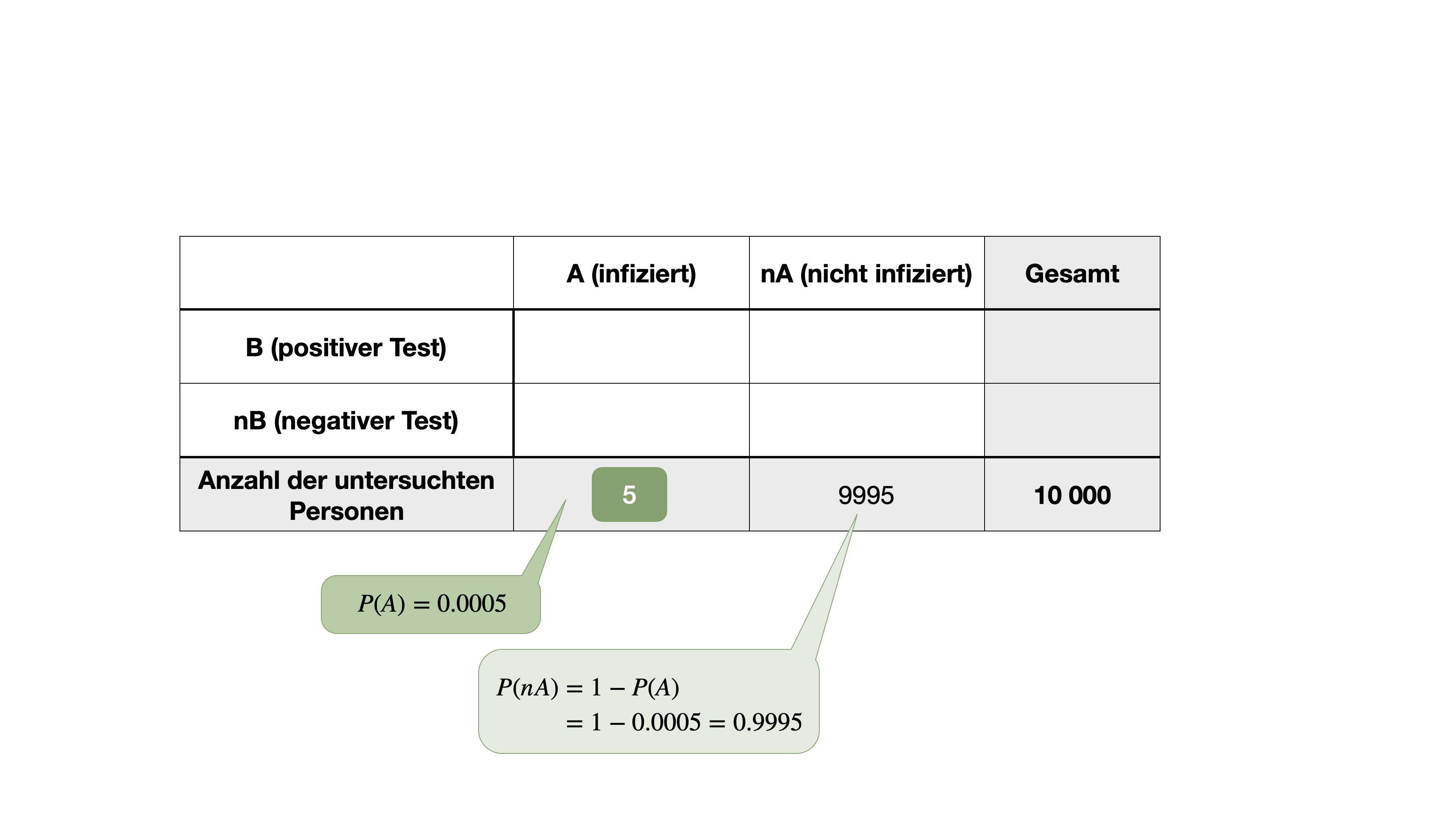
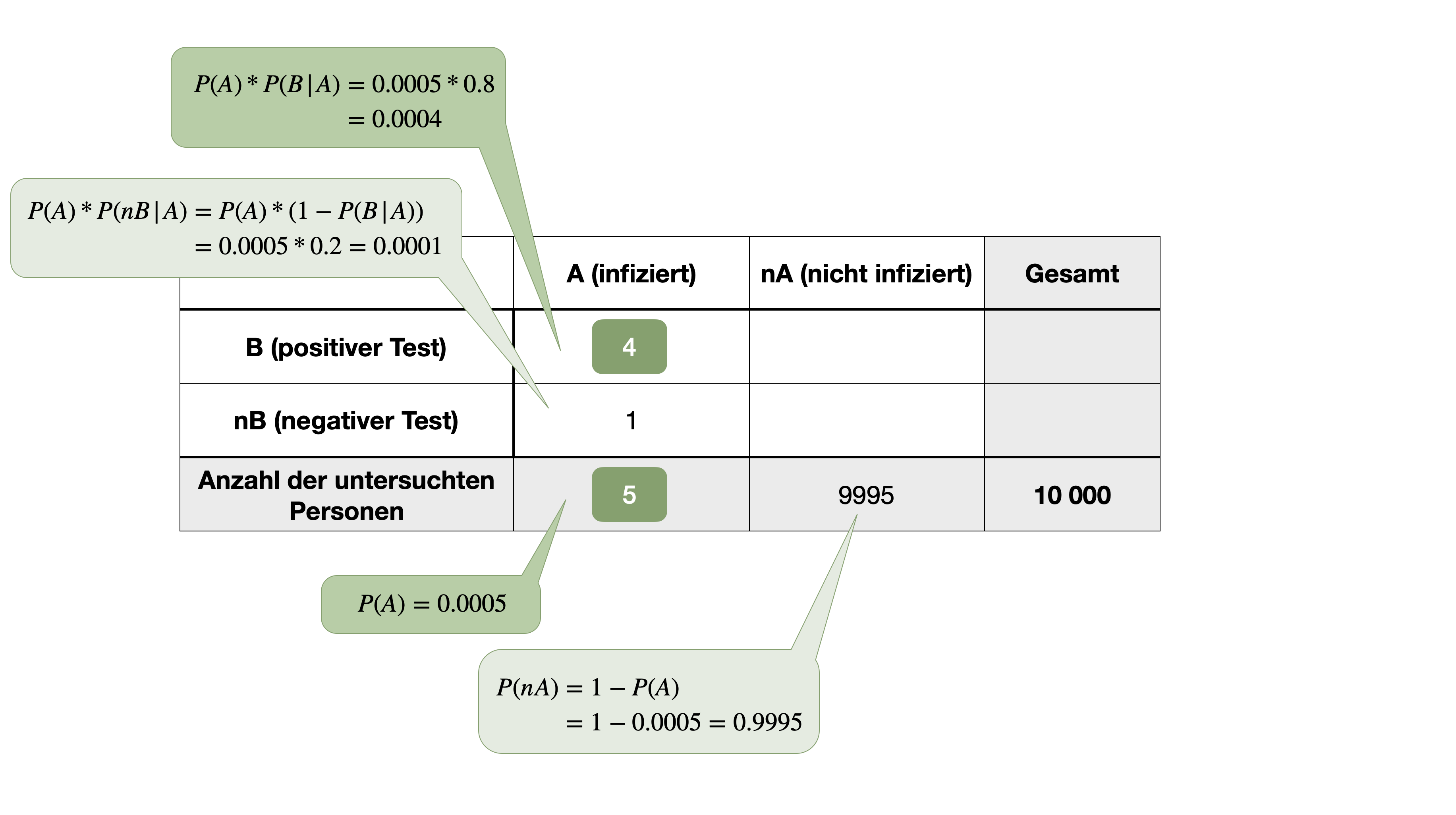
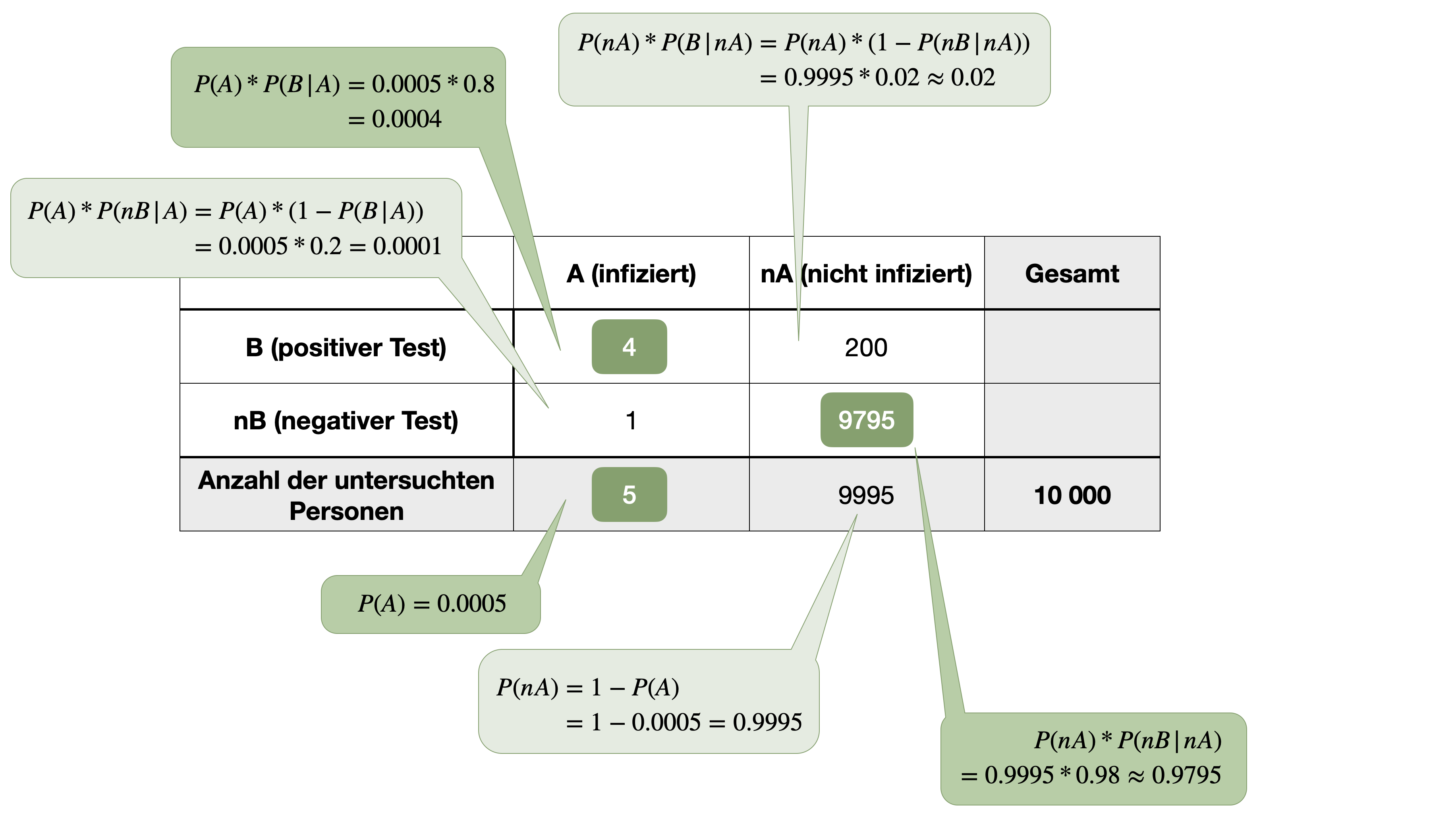
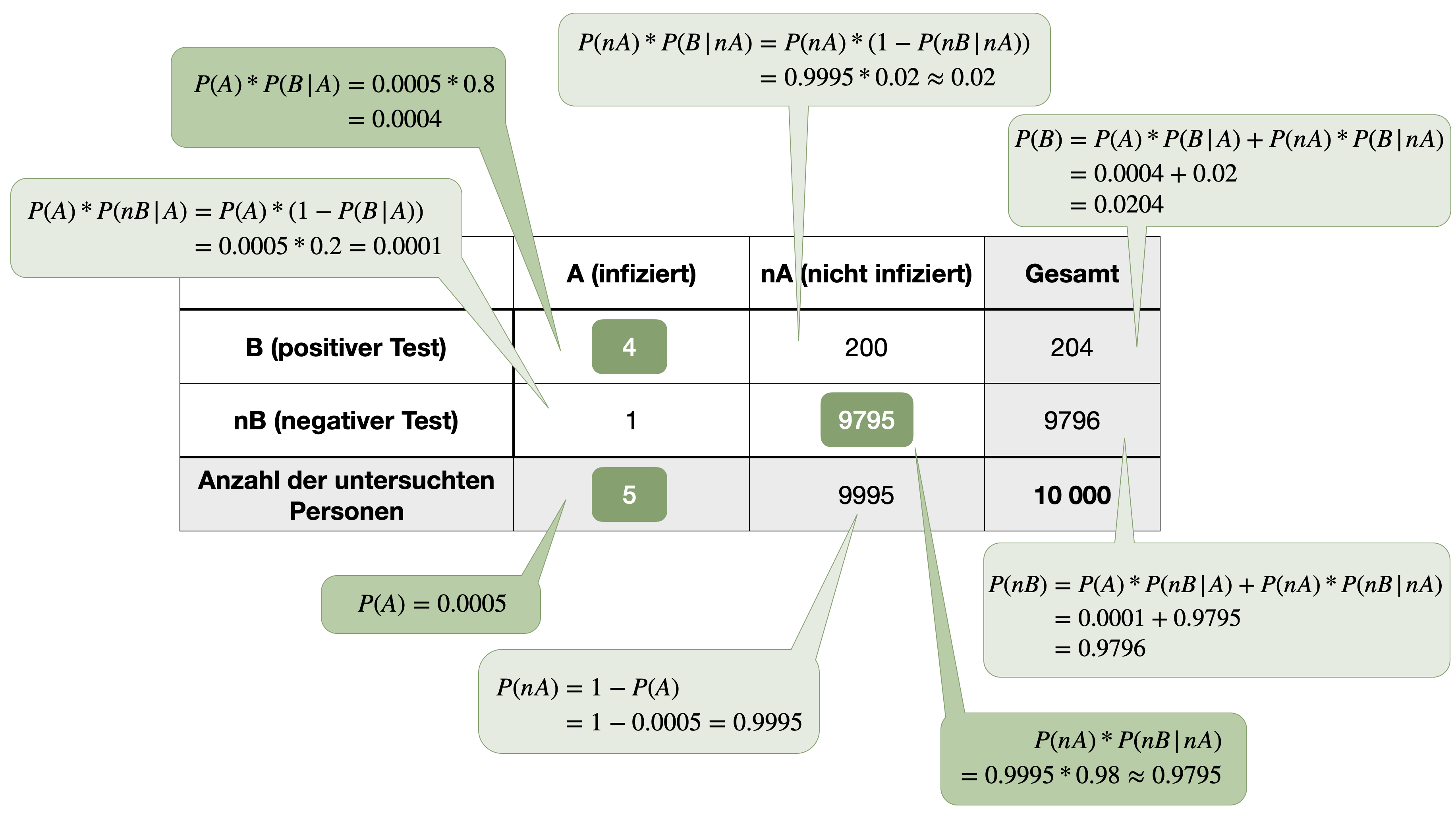
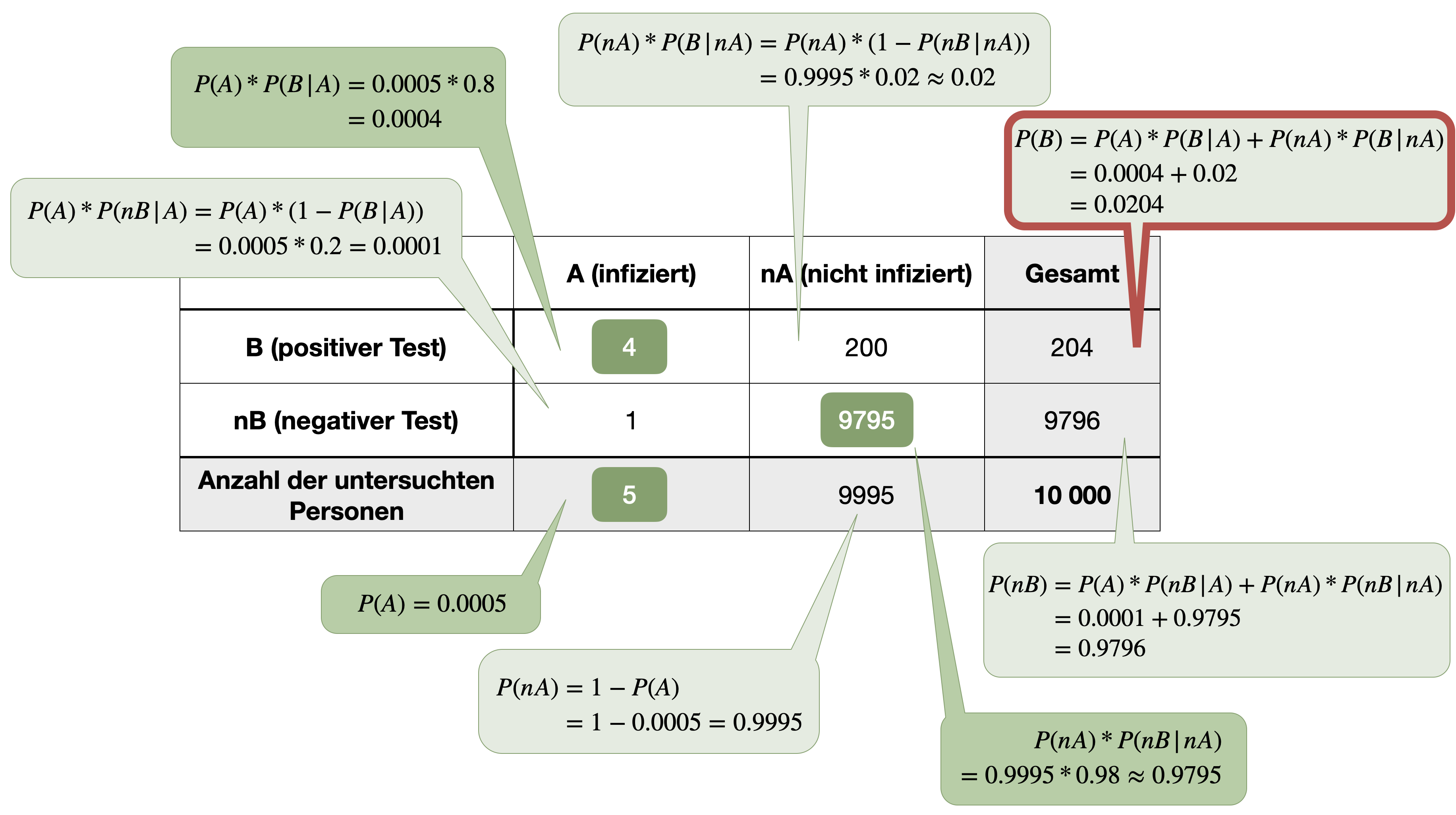
…gehört zu den wichtigsten Sätzen der Wahrscheinlichkeitsrechnung und wurde vom englischen Mathematiker Thomas Bayes entwickelt und 1763 in An essay towards solving a problem in the doctrine of chances veröffentlicht.

Bildquelle: Wikimedia Commons(CCO 1.0 Lizenz)

Übungsaufgaben

Übungstag 1

Wahrscheinlichkeitstheorie

• Aufgaben:
  • 1.1 Hausaufgabe zur Vorbereitung: Glücksspiele
  • 1.2 Einfache Berechnungen von Wahrscheinlichkeiten
  • 1.3 Bedingte Wahrscheinlichkeit und der Satz von Bayes
• R Notebook-Skript:
  • DS2_01_Uebungen_Wahrscheinlichkeitstheorie.Rmd

s. Handbuch - Abschnitt ‘Übungen’

Fragen?

Abschlussquiz

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de


Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.