x <- 10L
if ( is.integer(x) ) {
print(
"Yes, x is an integer!")
}[1] "Yes, x is an integer!"if ( is.double(x) ) {
x*2
}
Data Science 1 - Programmieren & Visualisieren
Saskia Otto & Monika Eberhard
Universität Hamburg, IMF
Wintersemester 2024/2025
![]()
Eine Übersicht der wichtigsten Funktionen gibt es hier:

Dieses wie alle anderen DSB Cheatsheets gibt es auf Moodle und der GitHub Repository uham-bio/Cheatsheets.
Es können neben Operatoren auch Funktionen in der Abfrage verwendet werden, solange diese ein TRUE oder FALSE zurückgeben.
if (Abfrage) {
mache folgendes
}
if (Abfrage) {
mache dies
} else {
mache das
}
Wenn bei der Abfrage TRUE rauskommt, wird die (erste) Anweisung ausgeführt.
Vergleichs- und Verknüpfungsoperatoren geben immer einen logischen Wert (TRUE oder FALSE) zurück.
![]()
# Beispieldatensatz mit Altersangaben
ages <- c(8, 25, 42, 60, 75, 30, 18, 5)
# Erstellung einer neuen Variable auf
# Grundlage des Alters
age_group <- character(length(ages))
# Bedingung innerhalb einer Schleife
for (i in 1:length(ages)) {
if (ages[i] < 18) {
age_group[i] <- "Child"
} else if (ages[i] >= 18 & ages[i] < 65) {
age_group[i] <- "Adult"
} else {
age_group[i] <- "Senior"
}
}
# Kombinieren beider Variablen
result <- data.frame(ages, age_group)age_group, auf der Grundlage der Altersinformationen im Altersvektor.result, enthält die ursprünglichen Altersangaben und die entsprechenden Altersgruppen.Diese Art von if-else-Logik wird häufig in der Datenanalyse verwendet und hilft bei der Kategorisierung von Daten in verschiedene Gruppen auf der Grundlage bestimmter Bedingungen.
ifelse()case_when()starwars %>%
select(name:mass, gender, species) %>%
mutate(
type = case_when(
height > 200 | mass > 200 ~ "large", # if..
species == "Droid" ~ "robot", # else if..
.default = "other" # else ..
)
)# A tibble: 87 × 6
name height mass gender species type
<chr> <int> <dbl> <chr> <chr> <chr>
1 Luke Skywalker 172 77 masculine Human other
2 C-3PO 167 75 masculine Droid robot
3 R2-D2 96 32 masculine Droid robot
4 Darth Vader 202 136 masculine Human large
5 Leia Organa 150 49 feminine Human other
6 Owen Lars 178 120 masculine Human other
7 Beru Whitesun Lars 165 75 feminine Human other
8 R5-D4 97 32 masculine Droid robot
9 Biggs Darklighter 183 84 masculine Human other
10 Obi-Wan Kenobi 182 77 masculine Human other
# ℹ 77 more rows![]()
01:30
![]()
![]()
Der Körper einer Bedingung (wie auch Schleife und Funktion) wird immer in geschweifte Klammern gesetzt, damit er über mehrere Zeilen gehen kann.
In der Abfrage muss ein Operator stehen, welcher die Abfrage wahr macht, denn der Codeblock in der Bedingung wird ja ausgeführt. Richtig ist daher:
Anhand der zweimaligen geschweiften Klammern wird deutlich, dass es sich um eine ‘if..else..’ Bedingung handelt.
An der Ausgabe 0 ist zu erkennen, dass der Alternativbefehl (in ‘else’) ausgeführt wurde. In die zweite Lücke muss daher ein Operator, bei der die Abfrage FALSE ergibt:

Eine Schleife enthält Code, der so lange ausgeführt wird, wie die Bedingung, die zur Schleife gehört, wahr ist. Der Code kann also z.B. zehn Mal ausgeführt werden, das hat den Vorteil, dass der Code nicht zehn Mal geschrieben werden muss.
for): führen eine bestimmte Anzahl an Wiederholungen aus, die durch einen Zähler oder einen Index kontrolliert wird. Dieser erhöht sich mit jeder Iteration.while) vs. fußgesteuerte/nachprüfende Schleifen (repeat): basieren auf ein Einsetzen und einer Verifikation durch eine logische Bedingung. Die Bedingung wird zu Beginn oder zum Ende des Schleifenkonstrukts getestet.for Schleife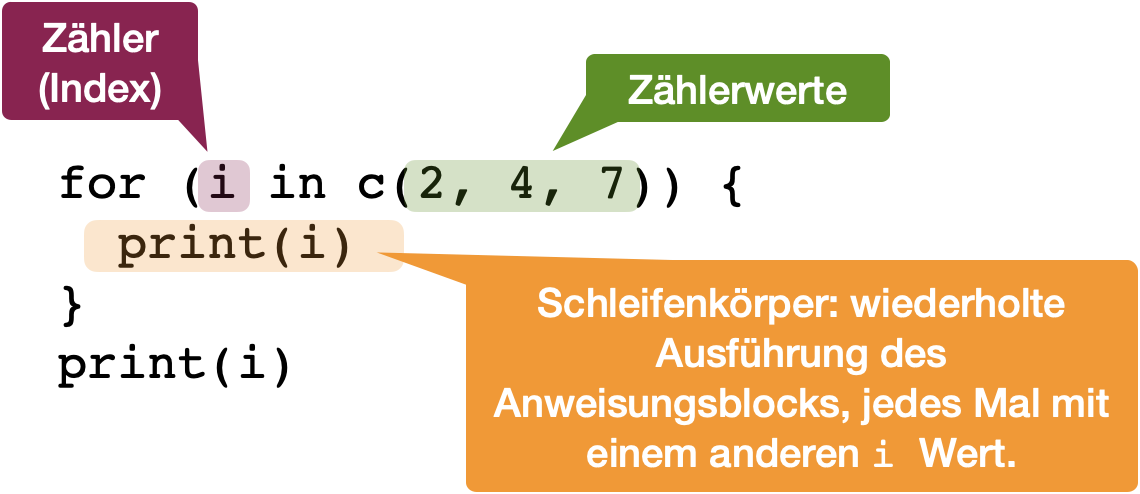
for Schleife
for Schleifefor Schleife - Stile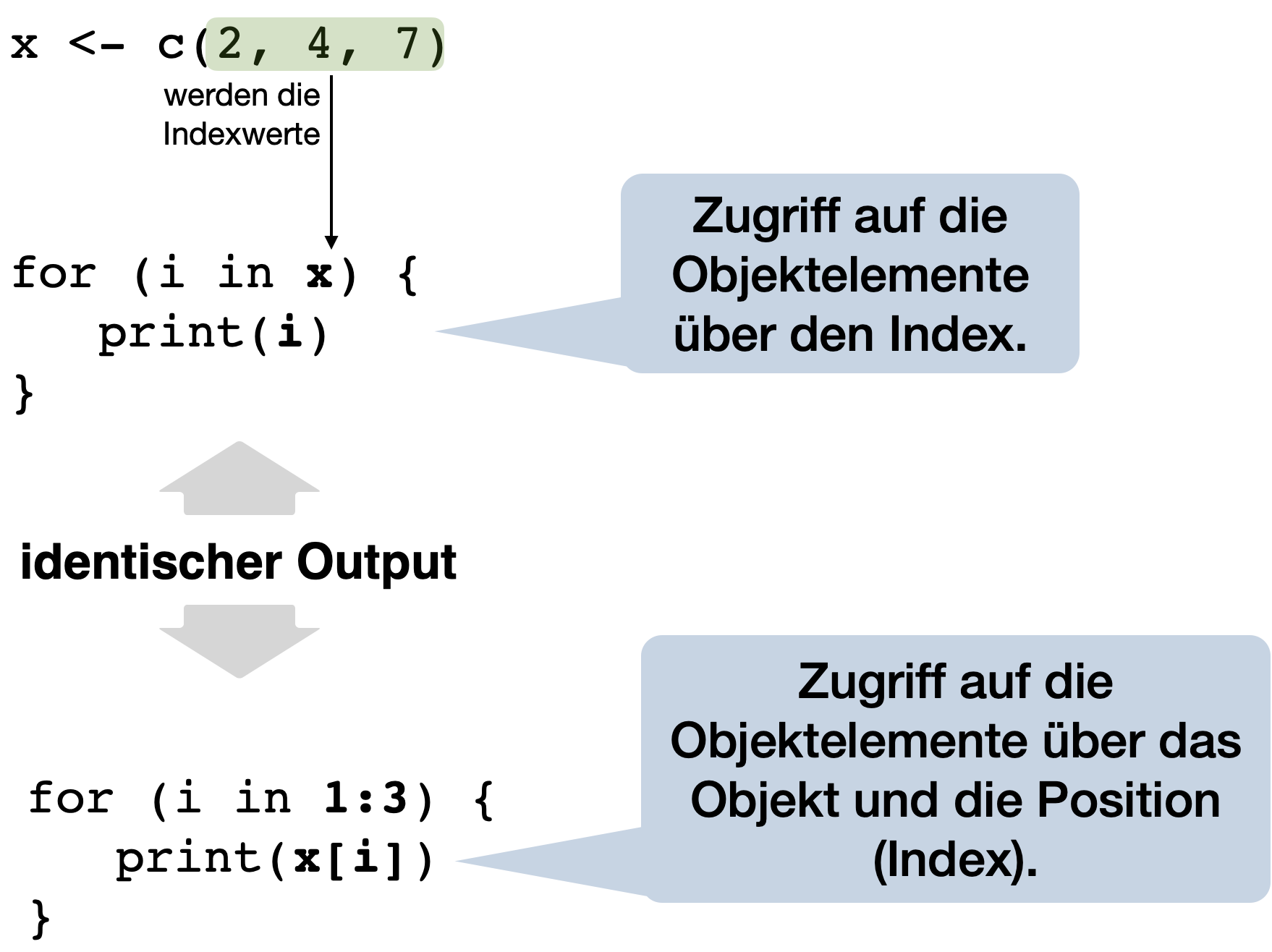
[1] 1 2 3[1] 2
[1] 4
[1] 7[1] 1 0[1] NA
numeric(0)→ 1:length() iteriert zumindest einmal!
for Schleife mit jeder Wiederholung mit z.B. c() wächst, wird die for Schleife sehr langsam werden:Testen wir die Geschwindigkeit der beiden Funktionen
Unit: milliseconds
expr min lq mean median uq max
grow_obj(500) 0.227181 0.236652 1.1734200 0.247230 1.519706 3.636331
grow_obj(5000) 25.784818 27.081935 27.9111518 28.075037 28.139120 30.474849
index_obj(500) 0.051127 0.057851 0.3215056 0.067404 0.071545 1.359601
index_obj(5000) 0.459282 0.476379 1.1939446 0.485768 0.525620 4.022674
neval cld
5 a
5 b
5 a
5 a In der Spalte mean ist zu sehen, dass die Variante mit der ‘Indexierung’ viel schneller ist als die mit wachsenden Objekten, besonders wenn viele Wiederholungen gemacht werden!
![]()
![]()
[1] "file_001.csv" "file_002.csv" "file_003.csv" "file_004.csv" "file_005.csv"
[6] "file_006.csv" "file_007.csv" "file_008.csv" "file_009.csv" "file_010.csv"Import aller 10 Dateien und Zusammenführung zu EINEM data frame
# Leere Liste für die importierten Datensätze
data_list <- vector("list", length = length(files))
# Schleife, bei der in jeder Iteration eine Datei importiert wird
for (i in seq_along(files)) {
data_list[[i]] <- read.csv(files[i])
}
# Zusammenfügen der einzelnen data frames in der Liste
data_df <- dplyr::bind_rows(data_list)'data.frame': 200 obs. of 3 variables:
$ station: chr "A" "A" "A" "A" ...
$ x : int 40 24 23 12 46 48 34 35 36 41 ...
$ y : num 28.93 14.49 1.67 9.51 20.64 ...# A tibble: 10 × 2
# Groups: station [10]
station n
<chr> <int>
1 A 20
2 B 20
3 C 20
4 D 20
5 E 20
6 F 20
7 G 20
8 H 20
9 I 20
10 J 20![]()
01:30
![]()
![]()
Anhand der Abfrage ist erkennbar, dass es sich um eine ‘while..’ Schleife handeln muss. Auch hier gilt wieder: der Schleifenblock gehört in geschweifte Klammern!
Und da eine ‘while..’ Schleife nur mehrere Iterationen durchgeht, wenn der Input in der Abfrage sich ändert, muss sich hier a im Schleifenkörper um den Wert erhöhen, den der Output sich erhöht (weil dieser a darstellt.)
Hier ist keine Abfrage jeweils zu sehen, sondern es wird ein Zählerindex definiert. Also muss es sich um die Zählschleife (‘for..’) handeln. Und zwar 2 ineinander verschachtelte. Wichtig ist hierbei, dass der Zähler unterschiedlich ist. Die erste Schleife hat meist den Index i, die nächste j, etc.).
Der innerste Schleifenkörper macht folgendes: es sollen die beiden Indizes zusammengefügt werden (mittels Funktion paste()) unter Verwendung des Trennzeichen ‘/’ . Damit dies auch wirklich in der Konsole sichtbar ist, braucht es aber die Funktion print(), welche als Input paste() enhält.
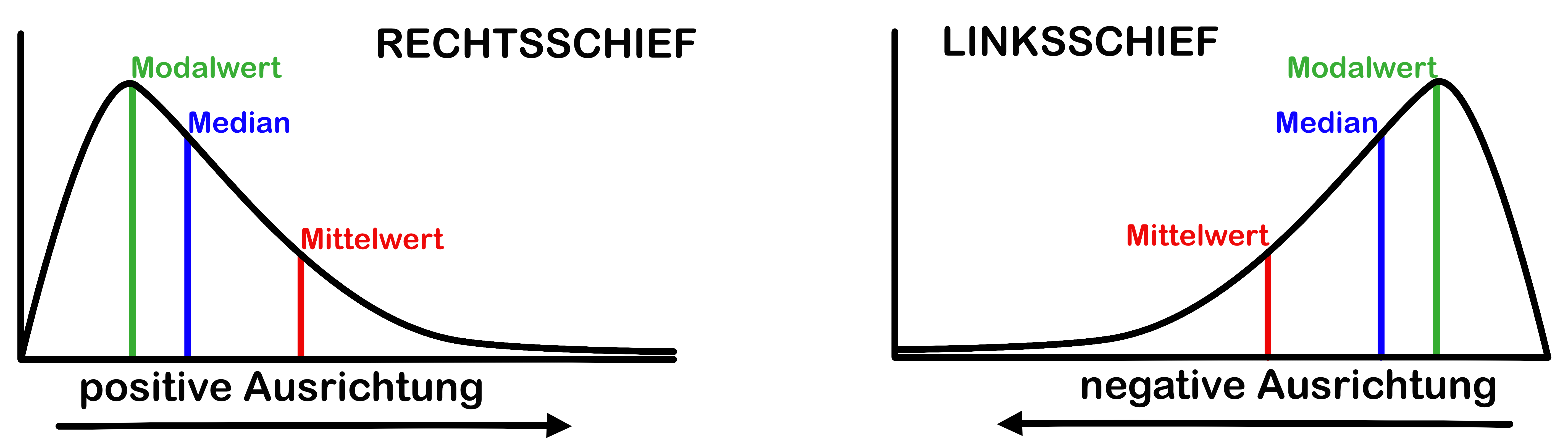
Es gibt drei Möglichkeiten, das Verhalten eines mathematischen Modells zu untersuchen, sobald wir uns für die Gleichung (oder den Satz von Gleichungen) entschieden haben, aus denen das Modell besteht.

Das diskrete logistische Wachstum mit Dichte-Abhängigkeit lässt sich mit folgender Gleichung beschreiben:
\[N_{t+1}=N_t+rN_t\left(1-\frac{N_t}{K}\right)\]



Nt <- 1 # neuer Start
# Grafik erstellen mit Startwert
plot(0, Nt,
xlim = c(0, 50), # t max = 50
ylim = c(0, 120), # weil K=100
col="black", pch = 16,
xlab = "Generation",
ylab = "Population size")
for (t in 1:50) {
Nt1 <- Nt + r*Nt * (1 - (Nt/K))
# neuen Wert in die Grafik fügen
points(t, Nt1,
col="red", pch = 16)
Nt <- Nt1
# Verzögerung der Simulation:
Sys.sleep(0.2)
}Hier mit 50 Zeiteinheiten:
![]()
02:30

![]()
![]()
\[N_{t+1}=N_t+rN_t\left(1-\frac{N_t}{K}\right)\]
N0 <- 1
N <- numeric(20)
N[1] <- N0
r <- 0.5
K <- 100
for (t in 2:20) {
N[t] <- N[t-1] + r*N[t-1] * (1 - (N[t-1]/K))
}
N [1] 1.000000 1.495000 2.231325 3.322093 4.927958 7.270514 10.641469
[8] 15.395999 21.908814 30.463241 41.054816 53.154734 65.604972 76.887397
[15] 85.772736 91.874293 95.607011 97.707014 98.827218 99.406732

Eine Funktion ist eine Sammlung von Code, die jederzeit über den jeweiligen Funktionsnamen aufgerufen werden kann. Sie können auch Parameter enthalten. Dies sind Werte, wie z.B. eine Zahl oder ein String. Diese Zahl kann von der Funktion wie eine Variable verwendet werden.
Output anpassbar
[1] "Hi Anne!"[1] "Hi Jan!"Error in sag_hi() : argument "name" is missing, with no defaultLasst uns nun eine Funktion bauen, die anhand einer Bedingung überprüft, ob die übergebene Zahl ein gerade oder ungerade Zahl ist. Dazu ist der sog. Restwert- oder Modulo-Operator %% für die Division mit Rest nützlich:
Zur Info: Eine Ganzzahldivision muss nicht unbedingt glatt aufgehen, wie z.B. bei 8/3. In diesem Fall gibt es den Rest 2 (6 lässt sich durch 3 teilen, bleiben 2 übrig). Diesen Rest liefert der Restwert-Operator.
\[\gamma_1 = \frac{\frac{1}{n}\sum\limits_{i=1}^{n} \left(x_{i} - \bar{x}\right)^{3}} {(\frac{1}{n}\sum\limits_{i=1}^{n} \left(x_{i} - \bar{x}\right)^{2})^{3/2}}\]
\[\gamma_1 = \frac{\frac{1}{n}\sum\limits_{i=1}^{n} \left(x_{i} - \bar{x}\right)^{3}} {(\frac{1}{n}\sum\limits_{i=1}^{n} \left(x_{i} - \bar{x}\right)^{2})^{3/2}}\]

Was machen wir, wenn der Vektor NAs enthält?
Wir führen ein weiteres Argument ein und bauen eine Bedingung in die Funktion!
[1] 0.3237934list() wird hier verwendet um Zwischenergebnisse zu einem Listenobjekt zu kombinieren, welches anschließend ausgegeben wird.
![]()
01:30
![]()
![]()
Die Funktion mit der eine Funktion definiert wird nennt sich function(). Um den Funktionskörper in einer nächsten Zeile anzeigen zu können und ggf. auch über mehrere Zeilen, braucht es die schweiften Klammern vorher und nachher.
Eine Funktion sollte nicht auf Skalare und andere Objekte zugreifen, die nicht innerhalb der Funktion definiert werden bzw. als Argument übergeben werden. Hier wird auf x und y zugegriffen, daher müssen diese als Argument definiert werden (function(x,y)). Das berechnete Produkt z wird explizit mit return(z) ausgegeben.

for Schleifen sind nicht so wichtig in R wie sie es in anderen Programmiersprachen sind, weil R eine funktionale Programmiersprache ist.for Schleifen in einer Funktion zusammenzuraffen und stattdessen die Funktion anzuwenden.




apply(), lapply(), sapply(), vapply(), tapply(), mapply()) macht genau das: Diese Funktionen wenden eine ausgewählte oder selbst definierte Funktion mit einer oder mehreren optionalen Argumenten auf Listen, Vektoren, ‘data frames’, Matrizen oder Arrays an.
Summe der 3 Spalten pro Zeile (Output als Vektor)
[1] 0.12799996 0.71241794 -0.06410025 0.16259230 0.26057783 -1.58409228
[7] 0.69621551 0.03610525 -0.01471492 0.99366090 3.26856660 -0.32497088
[13] 0.10755072 -3.39786802 1.18089506 1.52047173 -0.77770169 -0.15961181
[19] 2.49096619 1.22202247Summe der 3 Spalten pro Zeile (Output als Liste)
[[1]]
[1] 0.128
[[2]]
[1] 0.7124179
[[3]]
[1] -0.06410025
[[4]]
[1] 0.1625923
[[5]]
[1] 0.2605778
[[6]]
[1] -1.584092
[[7]]
[1] 0.6962155
[[8]]
[1] 0.03610525
[[9]]
[1] -0.01471492
[[10]]
[1] 0.9936609
[[11]]
[1] 3.268567
[[12]]
[1] -0.3249709
[[13]]
[1] 0.1075507
[[14]]
[1] -3.397868
[[15]]
[1] 1.180895
[[16]]
[1] 1.520472
[[17]]
[1] -0.7777017
[[18]]
[1] -0.1596118
[[19]]
[1] 2.490966
[[20]]
[1] 1.222022Diese Funktionen wenden eine Funktion auf einen Vektor oder eine Liste an:
lapply(X, FUN, ...)
# Output -> Liste
sapply(X, FUN, ..., simplify = TRUE, USE.NAMES = TRUE)
# Output -> Vektor, Matrix
vapply(X, FUN, FUN.VALUE, ..., USE.NAMES = TRUE)
# wie sapply() mit definiertem Typ von Rückgabewert
replicate(n, expr, simplify = "array")
# wrapper für sapply(), wird bei Simulationen genutztlapply()$Sepal.Length
[1] 5.1 4.9 4.7 4.6 5.0 5.4 4.4 4.8 4.3 5.8 5.7 5.2 5.5 4.5 5.3 7.0 6.4 6.9 6.5
[20] 6.3 6.6 5.9 6.0 6.1 5.6 6.7 6.2 6.8 7.1 7.6 7.3 7.2 7.7 7.4 7.9
$Sepal.Width
[1] 3.5 3.0 3.2 3.1 3.6 3.9 3.4 2.9 3.7 4.0 4.4 3.8 3.3 4.1 4.2 2.3 2.8 2.4 2.7
[20] 2.0 2.2 2.5 2.6
$Petal.Length
[1] 1.4 1.3 1.5 1.7 1.6 1.1 1.2 1.0 1.9 4.7 4.5 4.9 4.0 4.6 3.3 3.9 3.5 4.2 3.6
[20] 4.4 4.1 4.8 4.3 5.0 3.8 3.7 5.1 3.0 6.0 5.9 5.6 5.8 6.6 6.3 6.1 5.3 5.5 6.7
[39] 6.9 5.7 6.4 5.4 5.2
$Petal.Width
[1] 0.2 0.4 0.3 0.1 0.5 0.6 1.4 1.5 1.3 1.6 1.0 1.1 1.8 1.2 1.7 2.5 1.9 2.1 2.2
[20] 2.0 2.4 2.3
$Species
[1] setosa versicolor virginica
Levels: setosa versicolor virginica
![]()

Sie sind jetzt so weit, …
..dass Sie selbst versuchen können, eine Funktion für die Kurtosis und Schiefe und Standardfehler zu erstellen.


Dann testen Sie doch Ihr Wissen in folgendem Abschlussquiz…
![]()

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de

Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.
Kurswebseite: Data Science 1