Biologische Prozesse mathematisch beschreiben

Data Science 1 - Programmieren & Visualisieren

Saskia Otto & Monika Eberhard

Universität Hamburg, IMF

Wintersemester 2025/2026

Lernziele

Am Ende dieser VL- und Übungseinheit werden Sie

• den Unterschied zwischen Korrelation und Regression bzw. Kausalität kennen.
• die Kovarianz und den Pearson Produkt-Moment Korrelationskoeffizienten berechnen können.
• Begriffe wie Abweichungs-Summenquadrate und Modellgüte einordnen können.
• die Koeffizienten und das Bestimmtheitsmaß einer linearen Regression mittels Ordinary-Least-Square-Verfahren in Calc manuell und mit dem Statistik-Assistenten berechnen können.
• Säulendiagramme zur Darstellung von Gruppenvergleichen und Streudiagramme mit Trendlinien zur Visualisierung von Beziehungen erstellen können.

Auf Zusammenhänge testen

Korrelation

• Prüfen von Beziehungen ohne Kausalität.
• Das Skalenniveau kann ordinal oder metrisch sein.
• Beide Variablen sind zufällige Variablen, es wird keine manipuliert.
• Je nach Skalenniveau und Verteilung wird der Korrelationstyp gewählt.

Regression

• Prüfen von Beziehungen mit Kausalität.
• Beide Variablen müssen metrisch sein.
• Unterscheidet in
  • Abhängige oder Antwortvariable Y
  • Unabhängige oder erklärende Variable X; diese wird meist manipuliert.

Korrelation

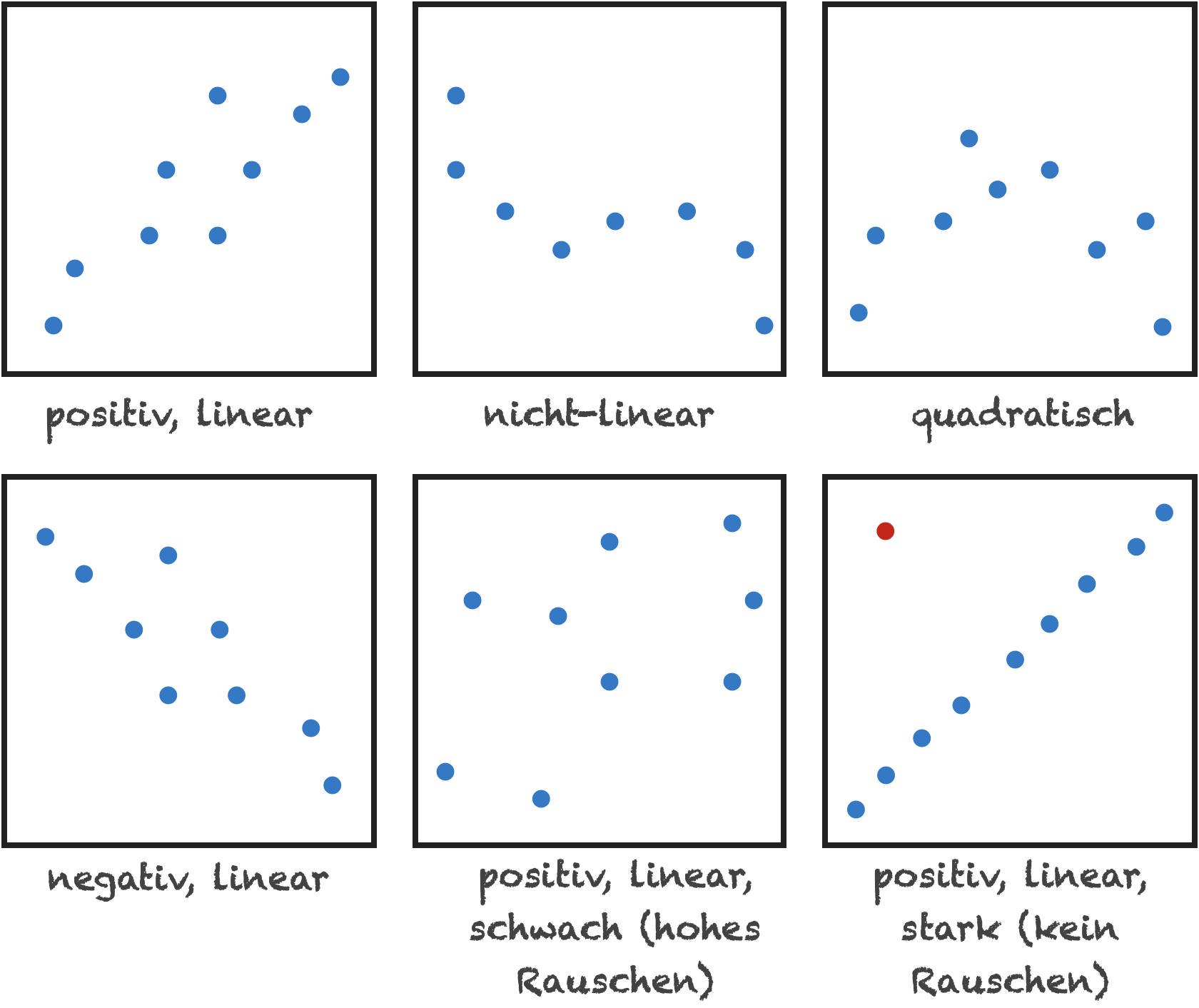
Charakterisierung bivariater Beziehungen

• Form (linear, nicht-linear, quadratisch)
• Richtung (positiv, negativ)
• Stärke (wie viel Streuung/Rauschen?)
• Ausreißer

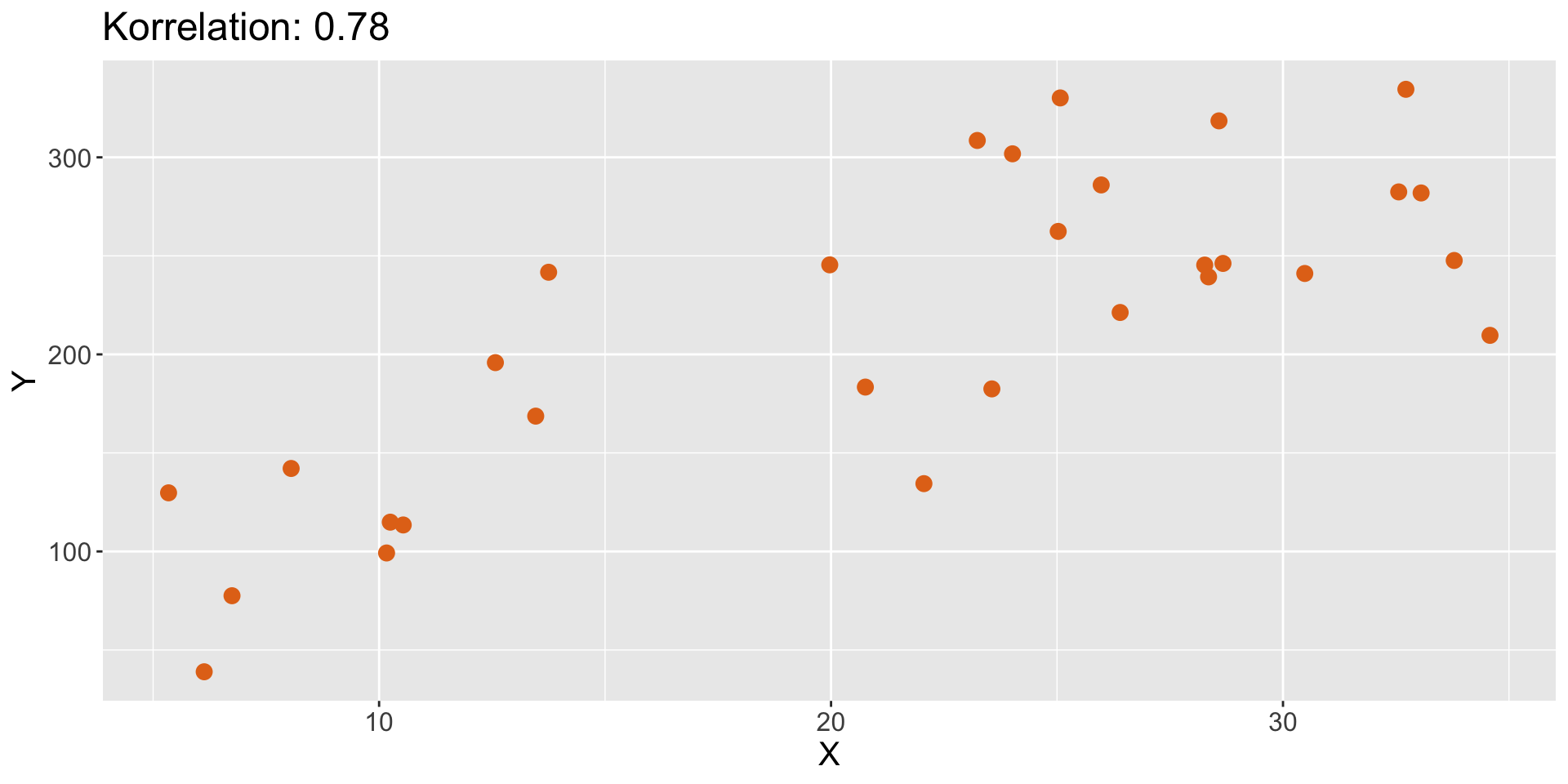
Quantifizierung der Stärke und Richtung von bivariaten Beziehungen

• Messgröße: Korrelationskoeffizient
• Wertebereich: -1 bis +1
  • Das Vorzeichen gibt die Richtung der Beziehung an.
  • Der Betrag die Stärke
    • 0 = keine Korrelation
    • -1 = starke negative Korrelation
    • +1 starke positive Korrelation

Important

→ Dies gilt allerdings nur bei linearen Zusammenhängen!

Verschiedene Arten von Beziehungen | 1

• positiv, linear, moderate Streuung

Verschiedene Arten von Beziehungen | 2

• nicht-linear (perfekte Beziehung, keine Streuung)

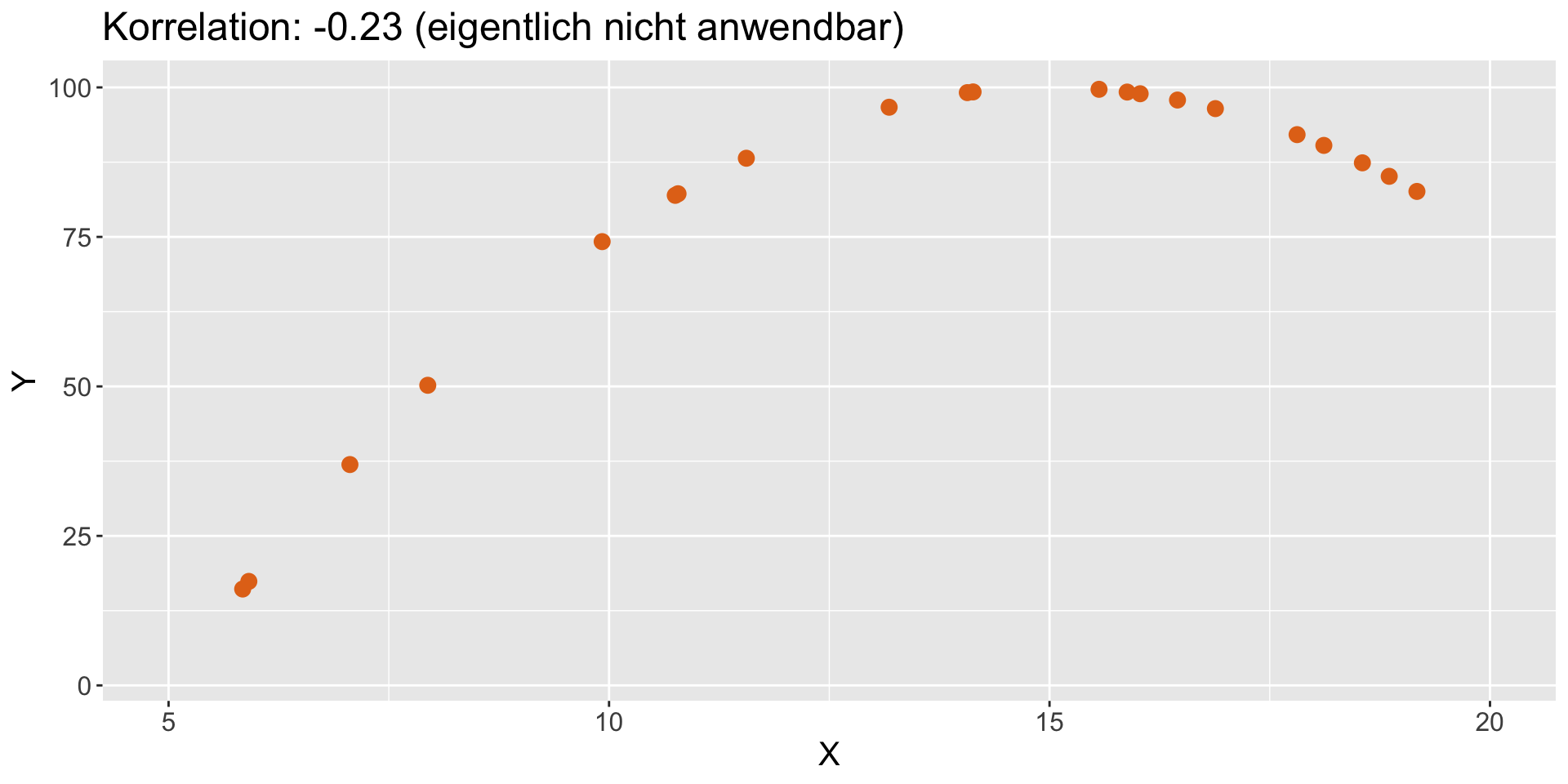
Verschiedene Arten von Beziehungen | 3

• perfekt linear mit Ausreißern

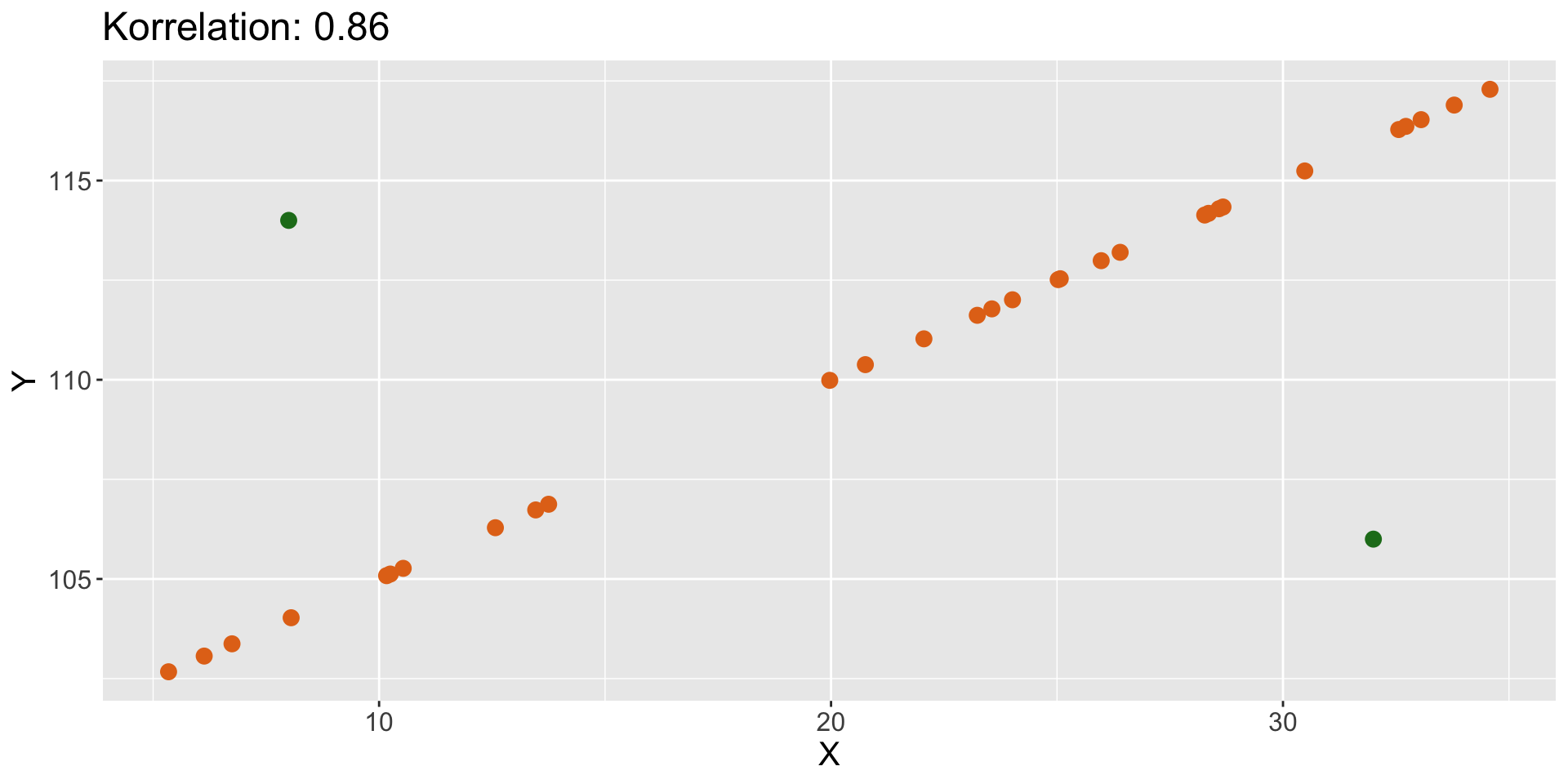
Verschiedene Arten von Beziehungen | 4

• keine Beziehung

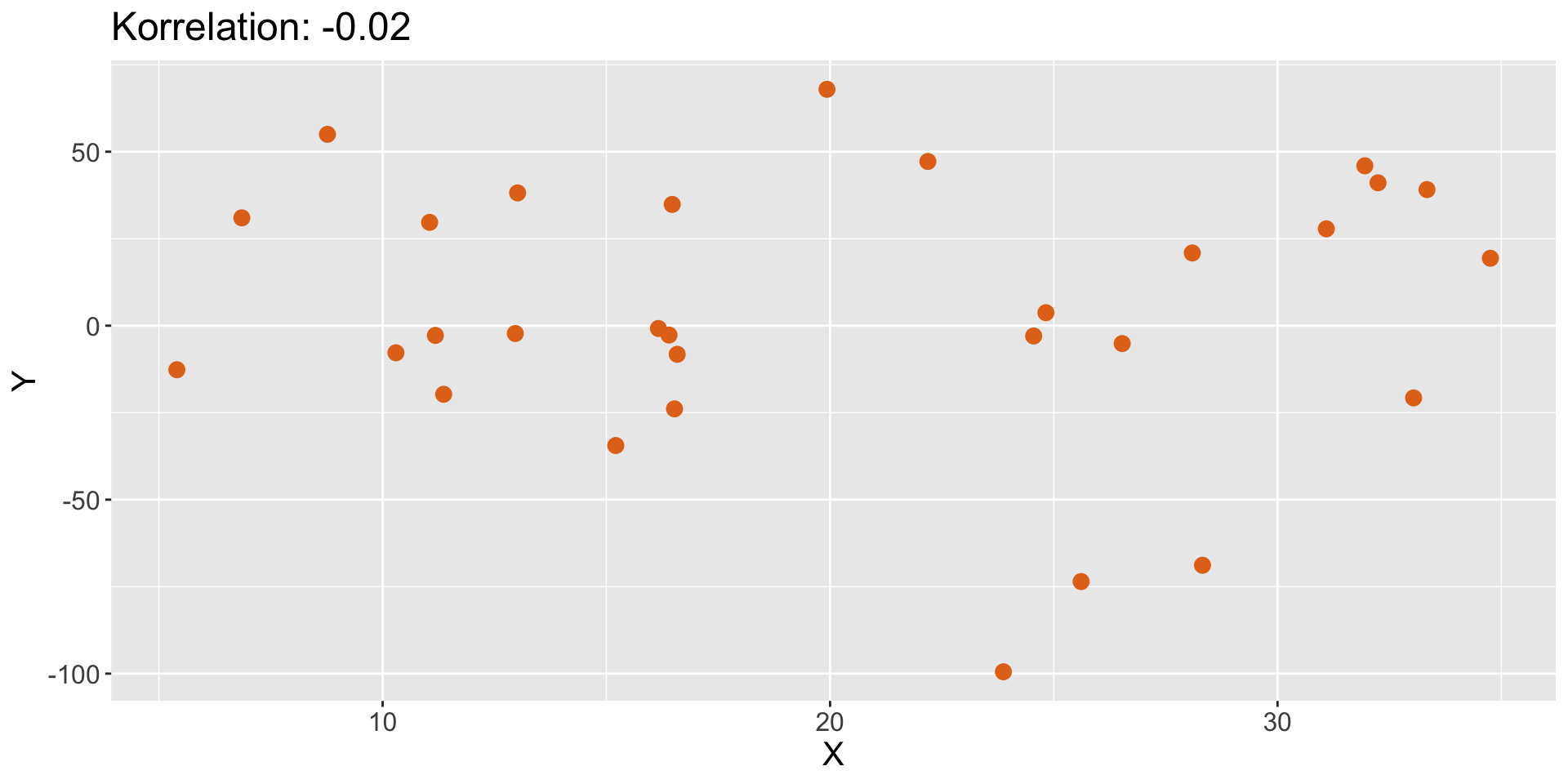
Korrelationsspiel

Mal sehen, wie gut Ihr “Bauchgefühl” über die Richtung und Stärke einer Korrelation ist:

Link zur Shiny-App: https://saskiaotto.shinyapps.io/correlation-game/

Ursache-Wirkung

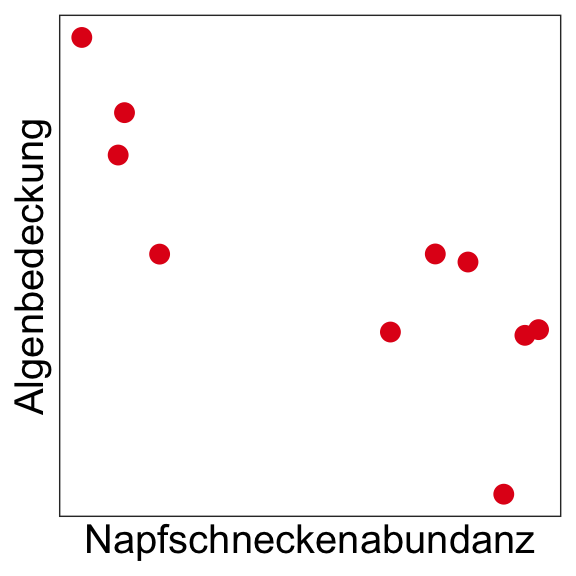
Negative Korrelation (Beziehung) zwischen der Napfschneckenabundanz und dem Grad der Algenbedeckung → Was könnte die Ursache sein?

Möglichkeit 1

→ Eine höhere Napfschneckenzahl ‘verursacht’ eine geringere Algenbedeckung durch Wegfraß.

Möglichkeit 2

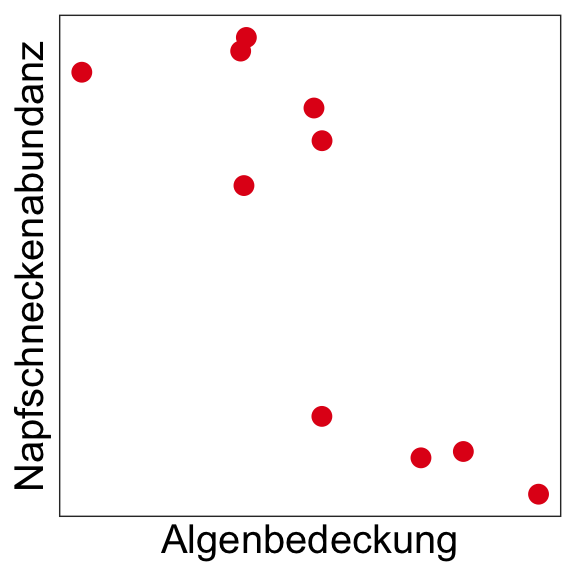
→ Ein hoher Algenbewuchs ‘verursacht’ eine geringere Napfschneckenzahl durch Konkurrenz um Platz.

Korrelation vs. Kausalität

Videolink: https://www.youtube.com/watch?v=VMUQSMFGBDo

Wie wird die Korrelation berechnet?

Streuungsparameter bei 1 vs. 2 Variablen

Varianz von X

s^{2} = \frac{1}{n-1}\sum\limits_{i=1}^{n}(x_{i} - \bar{x})^2 = \frac{1}{n-1}SS_X

Kovarianz zwischen X und Y

Cov(x,y)=\frac{1}{n-1}\sum\limits_{i=1}^{n}(x_i- \bar{x})(y_i- \bar{y}) = \frac{1}{n-1}SS_{XY}

Visualisierung der Summenquadrate | 1

SS_{X} bzw. ‘Sums of Squares of X’

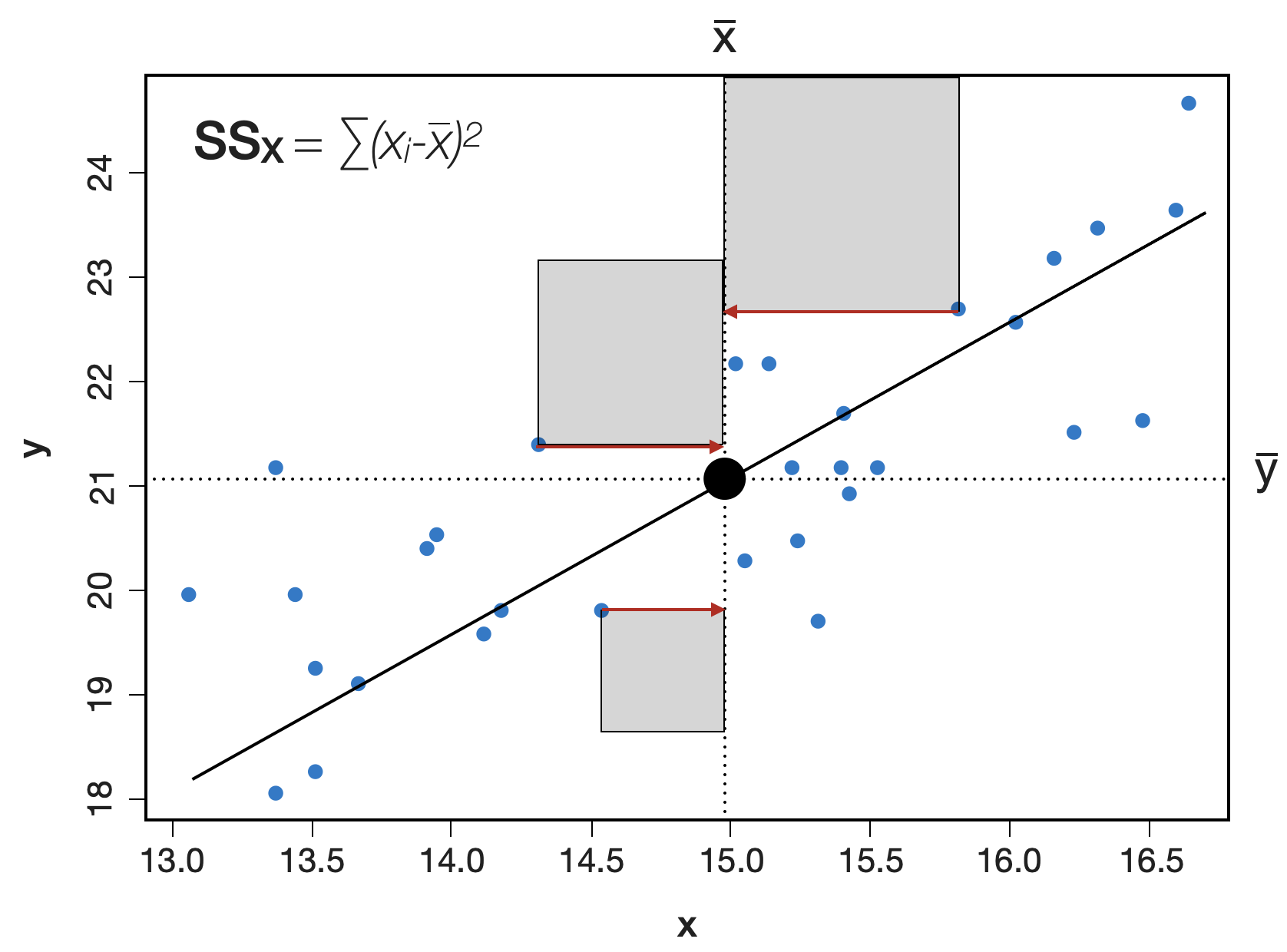
Visualisierung der Summenquadrate | 2

SS_{XY} bzw. ‘Sums of Squares of X and Y’

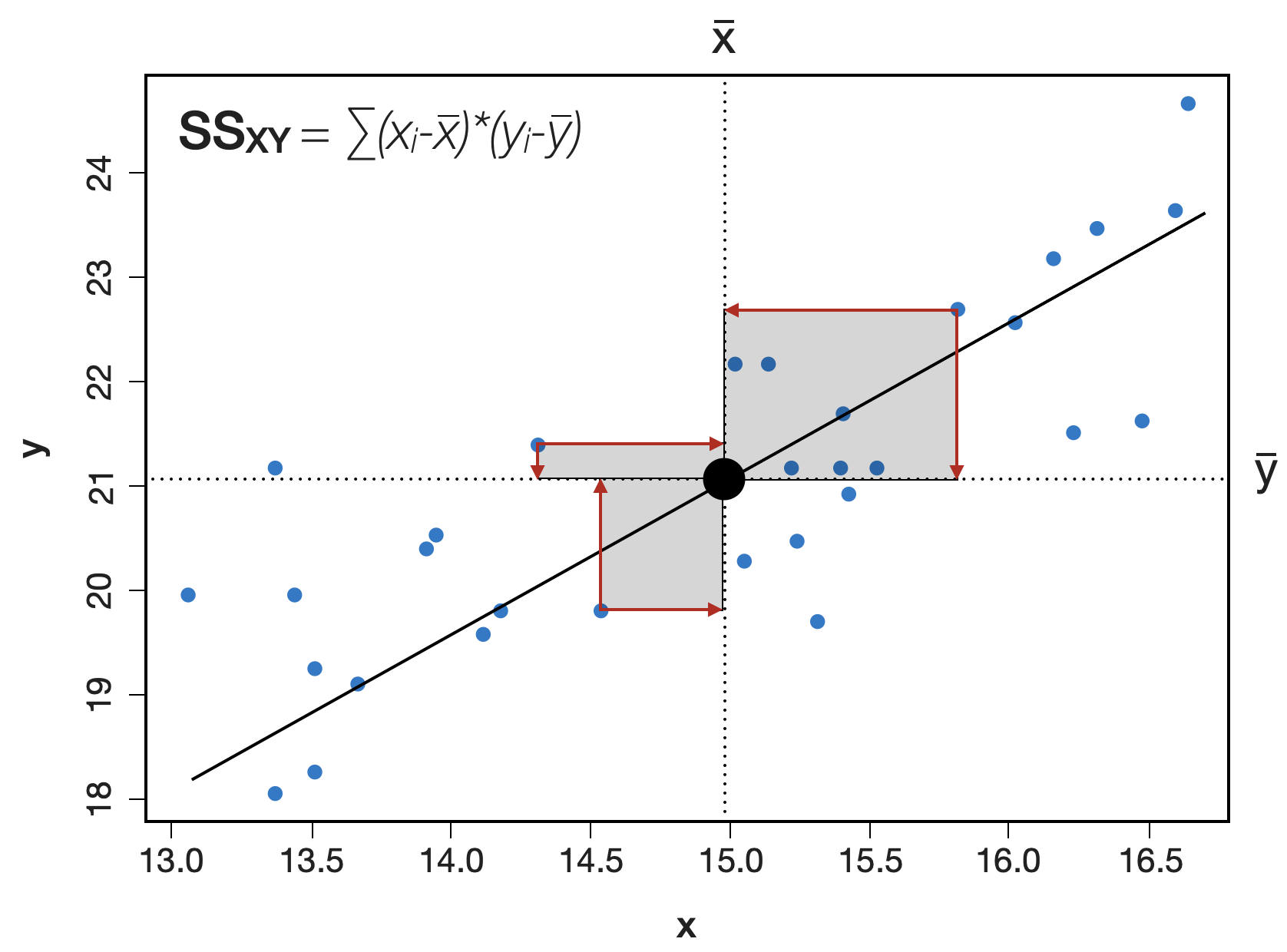
Standardisierung der Kovarianz

Kovarianz

• Ein Maß für die Stärke einer linearen Beziehung
• Einschränkung: absolute Größe hängt von den Einheiten der beiden Variablen ab.

Cov(X,Y)=\frac{1}{n-1}\sum\limits_{i=1}^{n}(x_i- \bar{x})(y_i- \bar{y})

Lösung: Maximale Kovarianz

• Standardisierung der Kovarianz mit den beiden Standardabweichungen, so dass das Maß der Stärke zwischen -1 und +1 liegt
  • → Pearson Produkt-Moment-Korrelationskoeffizient

Cov(x,y)_{max} = s_x*s_y

Parametrischer Korrelationskoeffizient

Pearson Produkt-Moment-Korrelationskoeffizient \rho

• Der Korrelationskoeffizient r (bzw. \rho für die Population) wird durch das Verhältnis zwischen der Kovarianz und der maximalen Kovarianz quantifiziert:

r_{x,y} = \frac{Cov(x,y)}{Cov(x,y)_{max}} = \frac{\frac{1}{n-1}\sum\limits_{i=1}^{n}(x_i- \bar{x})(y_i- \bar{y})}{s_x*s_y}

• r = \sqrt{R^2} → r ist die Quadratwurzel des “Bestimmtheitsmaßes” R^2
• r = [-1,+1] → R^2 ist immer positiv, während r die Richtung des Zusammenhangs angibt!

Biologische Prozesse mit Modellen beschreiben

Modelle

• sind eine simple Beschreibung einer komplexen Einheit (‘entity’) oder eines Prozesses.
• leiten sich von einer Hypothese ab → eine Hypothese kann viele Modelle produzieren.
• werden mit beobachteten Daten verglichen → dabei wird die Anpassungsgüte des Models an die Daten bewertet.

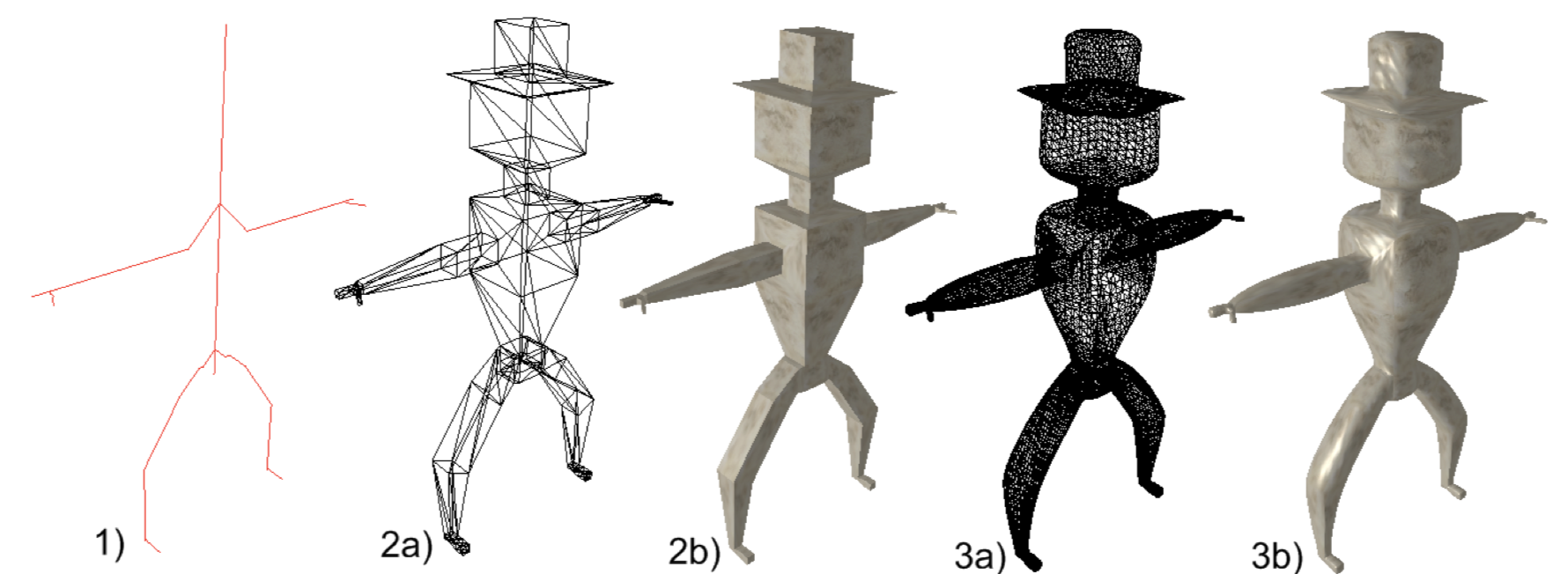
Bildquelle links: reality Baum von www.pixabay.com(CCO 1.0); Bildquelle rechts: ‘stick man graph’ von J. Nielsen (Masterarbeit: ‘Conversion of Graphs to Polygonal Meshes’, Technische Universität Kopenhagen, www.tchami.com)

Ziel der statistischen Modellierung

• Reduktion von Information / Vergleichbarkeit
• Identifikation der wichtigsten erklärenden Variablen (Prädiktor, Einflusswert, Wirkungsvariable; ‘predictor’)
• Bestimmung der Parameter-Werte, die erklärende (‘predictor’; X) und erklärte (‘response’, Y) Variablen verbindet
• Modell-basierte Vorhersagen machen

Kurvenanpassung

Die Kurvenanpassung (auch Ausgleichsrechnung oder Fit) ist eine mathematische Methode, gegebene (Mess-) Daten in möglichst einfacher analytischer Form darzustellen.

• Ausgangspunkt des Verfahrens ist die Wahl einer geeigneten Funktion, welche so gewählt werden sollte, dass eine möglichst genaue Übereinstimmung der berechneten mit den gegebenen (gemessenen) Daten erzielt wird.
• Für diese Optimierung wird üblicherweise die Methode der kleinsten Fehlerquadrate (sog. ‘Least Squares’-Verfahren) verwendet.
  • Bei dieser Methode werden die Parameter meist mittels Computer in einem iterativen Verfahren geschätzt.
• Das bekannteste Beispiel ist die lineare Regression.
  • Hier ist der Vorteil, dass sich die Parameter durch eine numerische Auflösung der linearen Gleichung berechnen lassen (‘Ordinary Least Squares’-Verfahren, OLS).

Biologische Modelle als Teilmodelle in komplexen Modellen

• In der Meereswissenschaft lassen sich z.B. Populations-Wachstumsmodelle mit physikalischen Ozeanmodellen koppeln, indem ein Temperaturterm in das Wachstumsmodell eingeführt wird.
• Moderne physikalische Ozeanmodelle berechnen in einem räumlichen 3D-Gitternetz für jeden Gitterpunkt in feinen Zeitschritten physikalische Parameter (Temperatur, Strömungsgeschwindigkeit, etc.).
• Mögliche Simulationen: z.B. Verfolgung des Wachstum von driftenden Fischlarven, die von unterschiedlichen Orten (Laichplätzen) starten → bieten bestimmte Laichorte für Larven besonders günstige Wachstumsbedingungen, da Verdriftung stets in wärmere Gebiete führt?

Biologische Modelle als Teilmodelle in komplexen Modellen | Beispiel

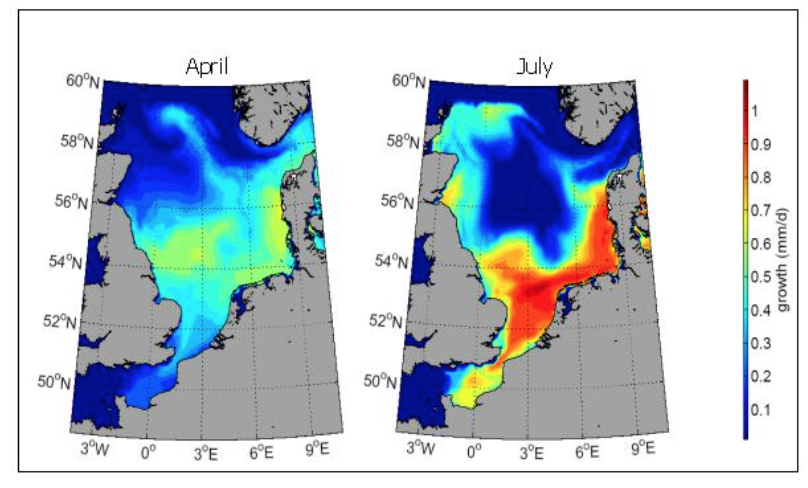
Berechnetes potentielles Wachstum von Sprottenlarven (Länge: 10mm) in Abhängigkeit von der Temperatur in einem 3D Ozeanmodell (Quelle: A. Temming)

Einfachstes Modell: Lineare Regression

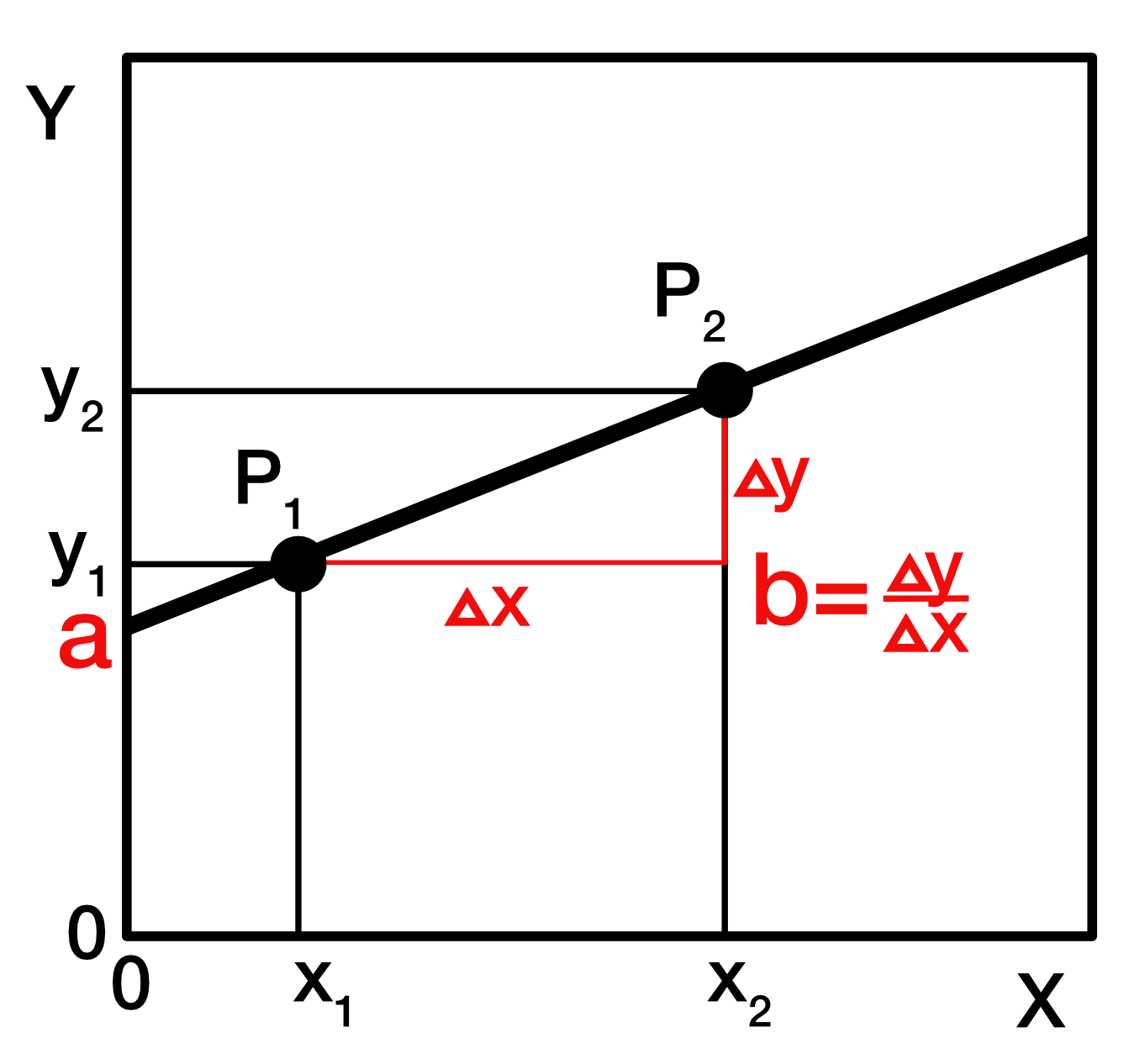
Funktion einer geraden Linie

y = a + bx

• y ist die abhängige Variable.
• x ist die unabhängige Variable.
• a ist der y-Achsenschnittpunkt, das ist der Wert an dem die Linie die y-Achse kreuzt (wenn x Null ist).
• b ist der Steigungskoeffizient und berechnet sich aus dem Quotienten der Differenz von y_1 und y_2 sowie von x_1 und x_2.
  • b gibt an, um wieviel y zunimmt (bzw. abnimmt), wenn x sich um 1 Einheit erhöht.

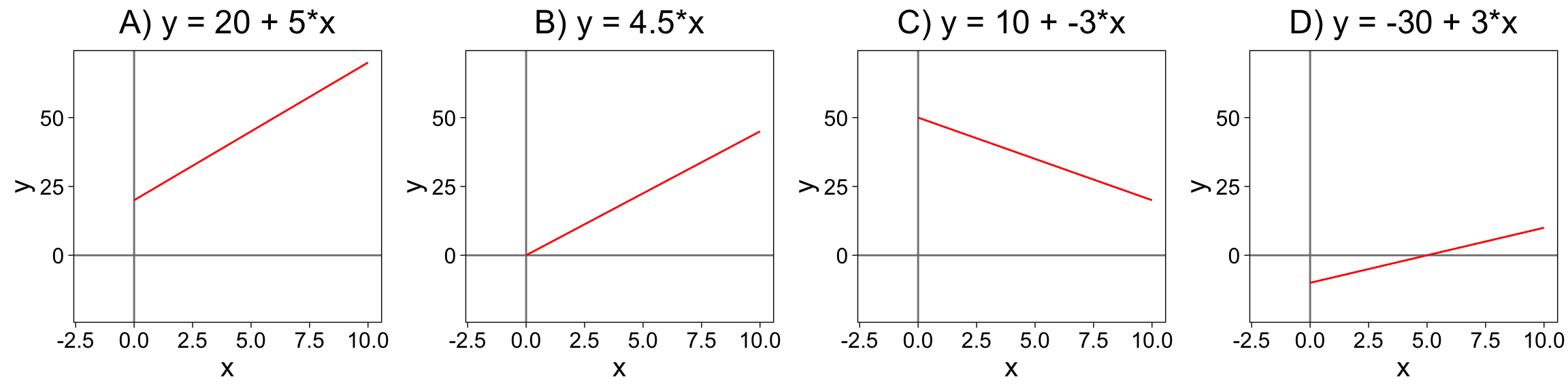
4 Typen der linearen Funktion

Ein Beispiel mit Zahlen

Typ A: Positive Steigung und
positiver Achsenabschnitt

• Zwei unabhängige Größen wirken additiv auf das Ergebnis (Y) ein.
• Achsenabschnitt a ist konstant, d.h. er ist unabhängig von der Ausprägung der Variable X.
• Der andere Term wächst proportional zur Variable X.
• Unabhängig bedeutet, das bei Wegfall des einen Terms der Effekt des anderen erhalten bleibt.

Beispiel: Eichgerade

• y = Extinktion
• x = Konzentration einer Lösung eines Stoffes
• a = Blindwert des Lösungsmittels (sowie möglichen Verunreinigungen der Küvette).
• Die Extinktion der Lösung addiert sich zu der Extinktion des gelösten Stoffes (bx).

Beispiel: Stoffwechselkosten

• y = Stoffwechselkosten eines fressenden Tieres
• x = Anzahl der erbeuteten Tiere
• a = Grundstoffwechsel des ruhenden Tieres
• b = energetische Kosten der Erbeutung (und Verarbeitung) eines Beutetieres (unter der impliziten Annahme, das die Beutetiere identisch sind)

Typ B: Positive Steigung, Achsenabschnitt Null

Hier wirkt nur ein Faktor auf die abhängige Variable ein. Man spricht auch von Proportionalität bei diesem Typ.

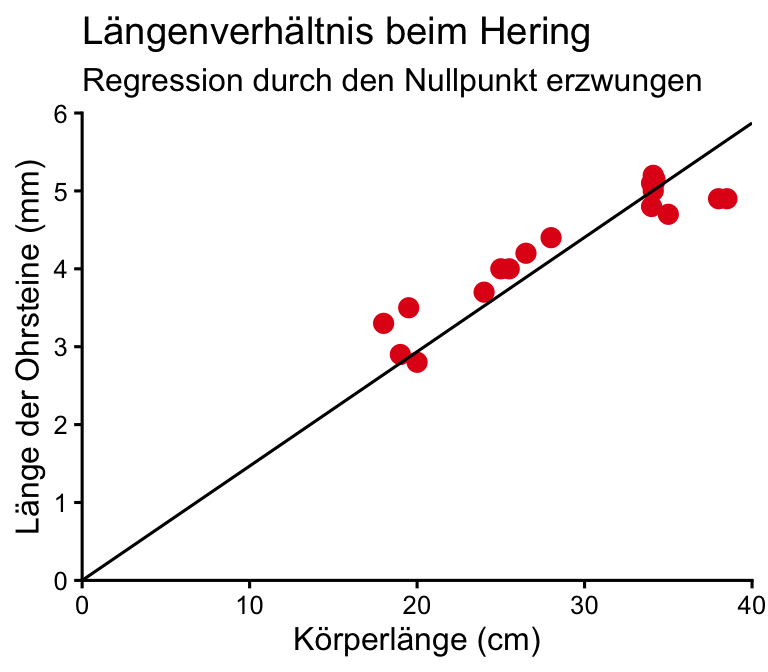
Beispiel: Isometrisches Wachstum

• Bei isometrischem Wachstum ändert ein Körper seine Gestalt nicht, er wächst unter Beibehaltung seiner Proportionen.
• Zum Nachweis kann man verschiedene Längenmaße in einer Grafik gegeneinander auftragen:

Typ C: Negative Steigung, positiver Achsenabschnitt

Beispiel: Energieabnahme eines hungernden Tieres mit der Zeit

• y = Körpergewicht des Tieres
• x = Zeit in Tagen
• a = Anfangsgewicht des Tieres zu Beginn der Hungerperiode
• b = entspricht dem Grundstoffwechsel pro Tag

Typ D: Positive Steigung, negativer Achsenabschnitt

Hier arbeiten zwei Prozesse gegeneinander, d.h. mit unterschiedlichem Vorzeichen.

Beispiel: Fischzuwachs

• y = täglicher Zuwachs in Energieeinheiten
• x = tägliche Futtermenge in Energieeinheiten
• a = Zuwachs bei Null Futtermenge → Verlust an Energie
• Wenn y=0 → bei der entsprechenden Futtermenge x_1 ist Zuwachs gerade Null (=Erhaltungsration in Energieeinheiten).
• b = Effizienz, mit der jede zusätzliche Menge an Nahrungsenergie in Energiezuwachs des Fisches umgesetzt wird.

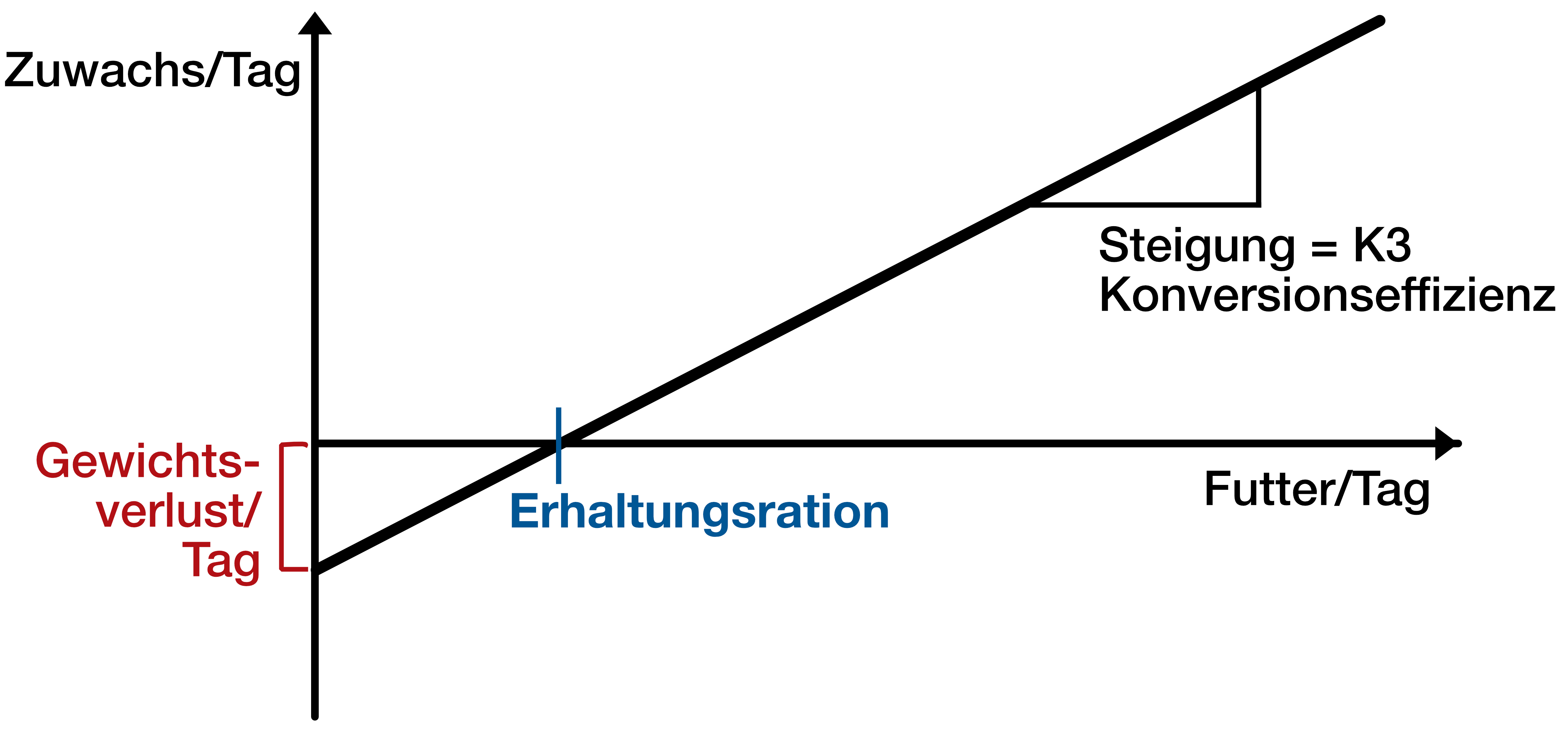Die beiden gegeneinander arbeitenden Prozesse sind die Energiezufuhr durch die Nahrung (positives Vorzeichen) und der Energieverbrauch durch den Erhaltungsstoffwechsel.

Wie werden a und b berechnet?

Das mathematische Werkzeug, dass dahinter steckt:

• Gewöhnliche Methode der kleinsten Fehlerquadrate = Ordinary Least Squares (OLS)
• OLS findet die Parameter a und b, basierend auf der Minimierung der Abweichungs-Summenquadrate (‘residual sums of squares’ = SS_{Residual}).

SS_{Residuen}=\sum e_i^2=\sum((a+b*x_i)-y_i)^2\rightarrow MIN

Regression durch den Achsenursprung

Typ B

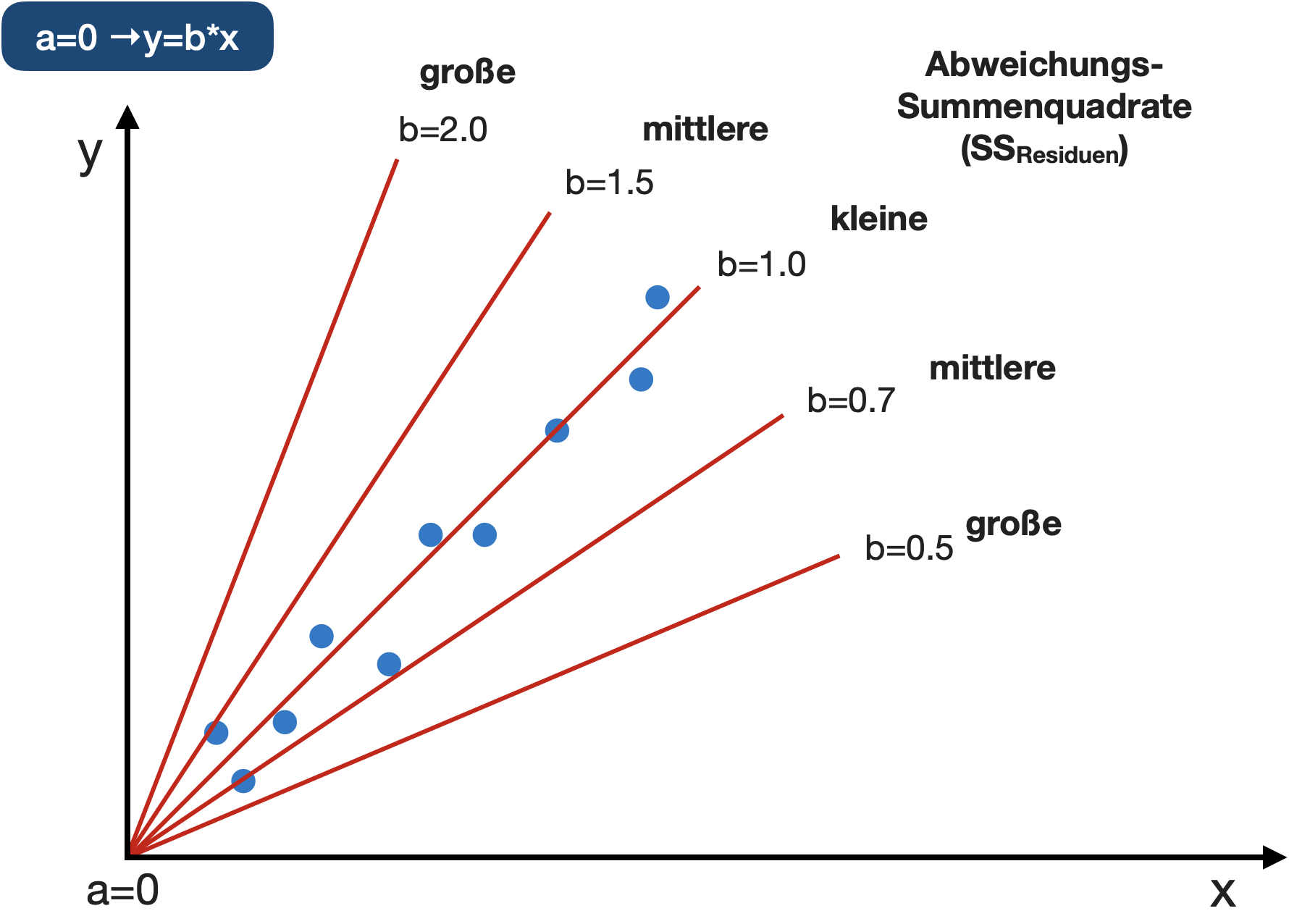
Abweichungs-Summenquadrate

Wenn a = 0

SS_{Residuen}=\sum e_i^2=\sum((b*x_i)-y_i)^2

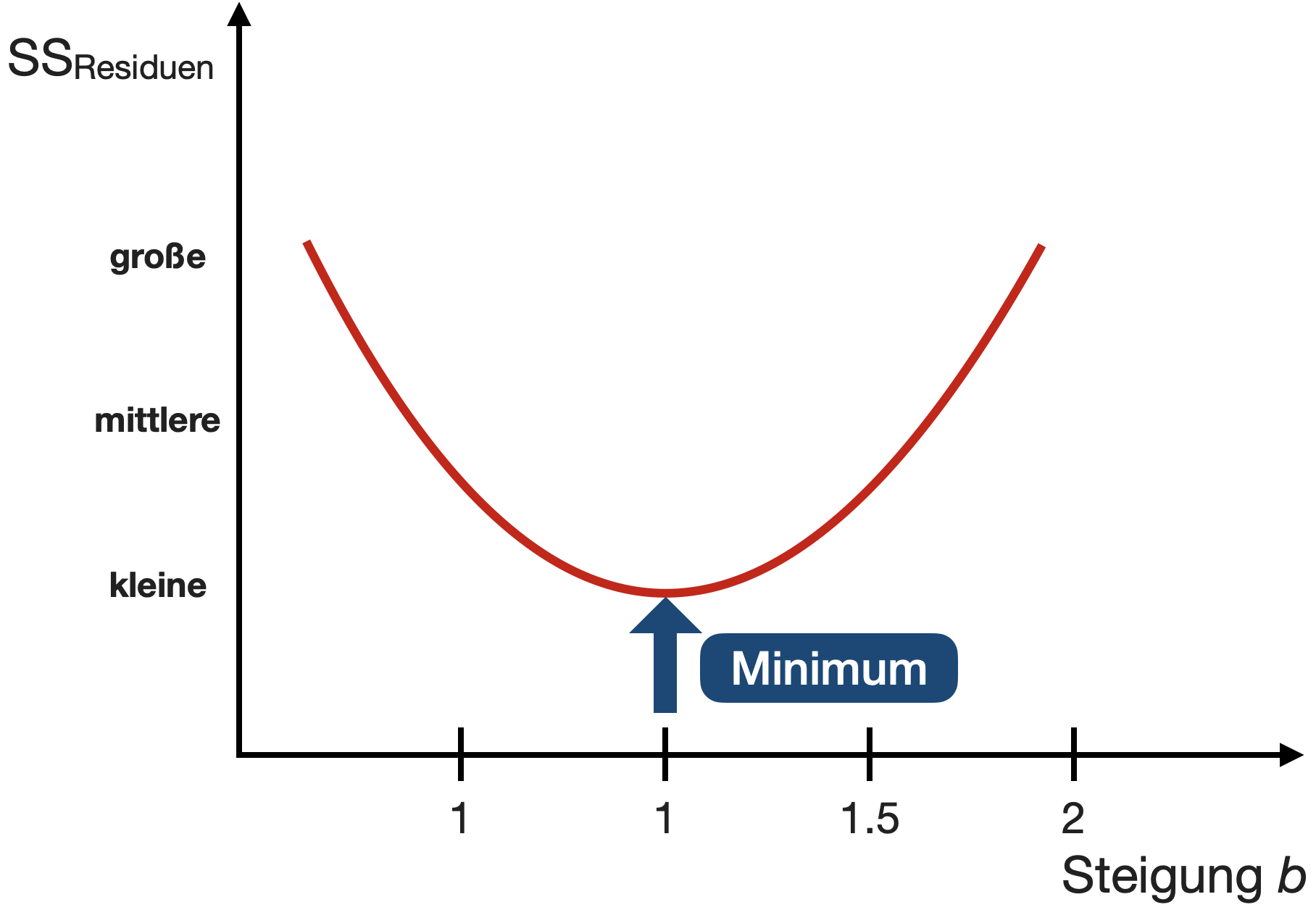
Minimierung der SS_{Residuen} | numerisch

Bildung der 1. Ableitung nach b und anschließend Null setzen:

SS_{Residuen}=(b*x_1-y_1)^2+(b*x_2-y_2)^2+.... | Binomialgleichung anwenden

SS_{Residuen}=b^2x_1^2-2bx_1y_1+y_1^2 + b^2x_2^2-2bx_2y_2+y_2^2 +.... | davon die 1. Ableitung

\frac{dSS_{Residuen}}{db}=2bx_1^2-2x_1y_1 + 2bx_2^2-2x_2y_2 +... | wieder als Summen schreiben

\frac{dSS_{Residuen}}{db}=2bx_1^2+2bx_2^2+...-2x_1y_1-2x_2y_2-...
\frac{dSS_{Residuen}}{db}=2b\sum x_i^2 - 2\sum x_iy_i | Null setzen und nach b auflösen

0=2b\sum x_i^2 - 2\sum x_iy_i
2\sum x_iy_i = 2b\sum x_i^2 | durch 2 und Summe x^2 teilen

b=\frac{\sum x_iy_i}{\sum x_i^2} → Formel für die Steigung b mit a = 0

Hinweis: alle x und y Werte sind Konstanten

Parameterschätzung bei Typ A

Analog zu Regressionstyp B werden die Parameter mittels partieller Ableitungen und Gleichsetzung mit Null ermittelt. Bei der Bildung einer partiellen Ableitung z.B. nach a wird die andere Variable wie eine Konstante behandelt (und umgekehrt).

Steigung b

\begin{align} b&=\frac{\sum x_i*y_i}{\sum x_i^2}\\ &= \frac{\sum[(x_i-\bar{x})*(y_i-\bar{y})]}{\sum(x_i-\bar{x})^2} \\ &= \frac{SS_{XY}}{SS_{X}} \Rightarrow \frac{Cov_{XY}}{s_{x}^2}\\ \end{align}

y-Achsenabschnitt a

→ Da die Regressionslinie durch das Zentrum der Datenwolke geht (also durch den Mittelwert von x und y), braucht diese Formel nur nach a umgeformt werden:

\bar{y} = a+b\bar{x} \Rightarrow a = \bar{y}-b\bar{x}

Varianzzerlegung in linearen Modellen

Die Gesamtstreuung (SS_Y oder SS_{Gesamt}) kann in 2 Komponenten zerlegt werden:

erklärbare Streuung = SS_{Regression} + nicht erklärbare Streuung = SS_{Residuen}

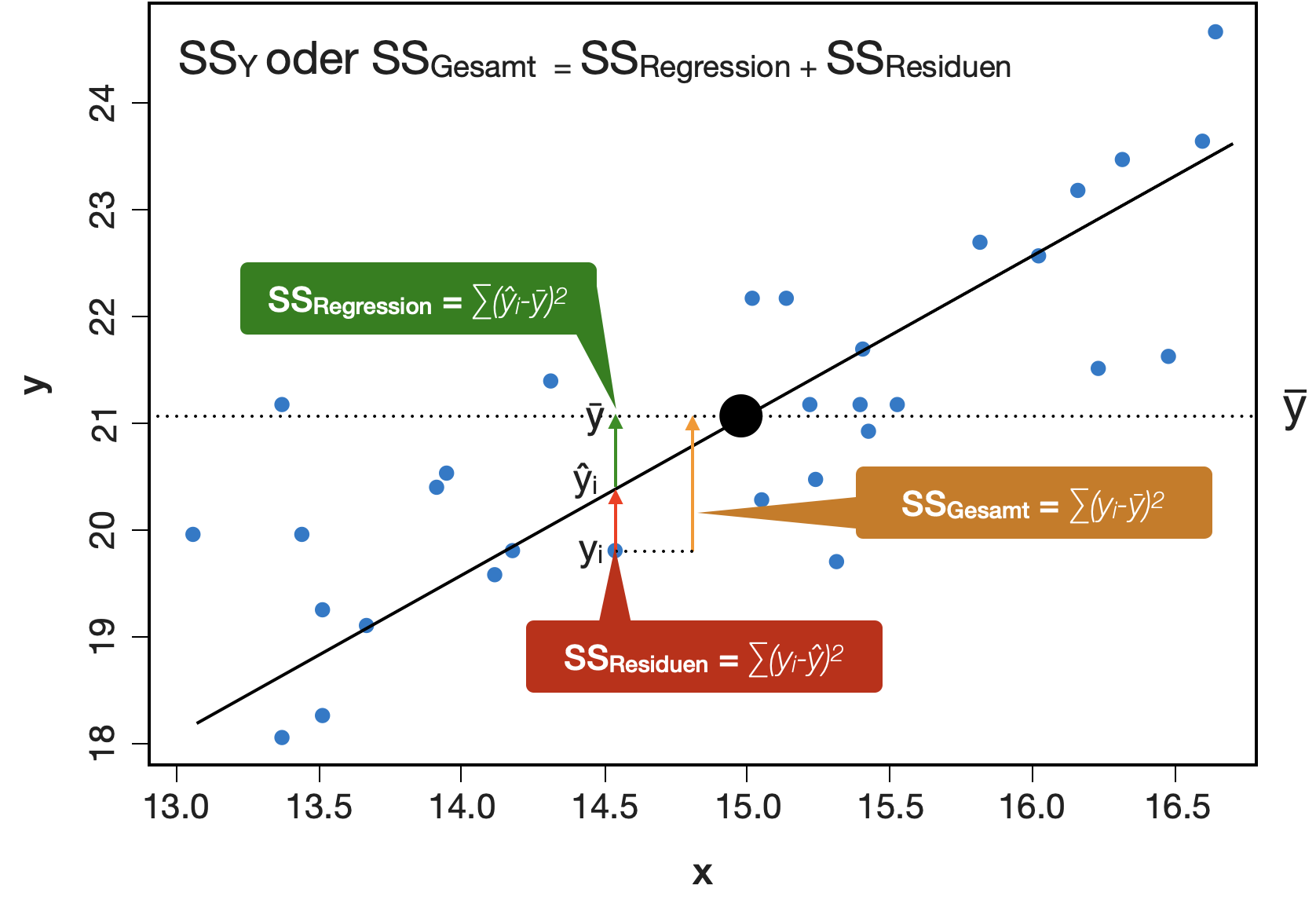
Wie gut ist das Modell?

Bestimmtheitsmaß R^2

Die statistische Kenngröße R^2 ist ein Maß für den Anteil der Variabilität in y, welcher durch das lineare Modell erklärt werden kann:

R^2 = \frac{SS_{Regression}}{SS_{Gesamt}} = \frac{\sum(\hat{y}_i-\bar{y})^2}{\sum(y_i-\bar{y})^2} 1 \geq R^2 \geq 0

• Werte nahe 1 weisen auf eine sehr gute Beschreibung der Daten.
• Werte nahe 0 weisen auf eine sehr hohe Streuung der Daten um die Gerade an
• Bei R^2=1 lägen alle Datenwerte exakt auf der Geraden.
• In der Ökologie wird bereits ein R^2 von 0.5 bzw. 50% als sehr gut erachtet.
• R^2=1 ist auch das Quadrat des Korrelationskoeffizienten r

Übungsaufgabe

Übungsskript Woche 3

Das Übungsskript und alle weiteren Dateien stehen im Moodle-Kurs als ZIP-Datei zur Verfügung!

Übungsskript Woche 3

Das Übungsskript und alle weiteren Dateien stehen im Moodle-Kurs als ZIP-Datei zur Verfügung!

Wie fühlen Sie sich jetzt…?

Total konfus?

Keine Sorge…

… dieses Thema wird nochmal in den Modulen Data Science 2, 3 und 4 aufgegriffen und vertieft.

Total gelangweilt?

Dann testen Sie doch Ihr Wissen in folgendem Abschlussquiz…

Abschlussquiz

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de


Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.