| A | B |
|---|---|
| 5 | 8 |
| 4 | 7 |
| 4 | 7 |
| 3 | 7 |
| 3 | 7 |
| 3 | 7 |
| 3 | 5 |
| 3 | 3 |
| 3 | 3 |
| 2 | 3 |
| 1 | 3 |
| 1 | 2 |

Grundlagen der deskriptiven Statistik
Data Science 1 - Programmieren & Visualisieren
Saskia Otto & Monika Eberhard
Universität Hamburg, IMF
Wintersemester 2025/2026
Lernziele
![]()
Am Ende dieser VL- und Übungseinheit werden Sie
- die wesentlichen Lage- und Streuungsparameter der numerischen deskriptiven Statistiken berechnen können.
- die Normalverteilung als wichtigste Wahrscheinlichkeitsverteilung und ihre Eigenschaften kennen.
- das Histogramm, das Säulendiagramm und den Box-Whisker-Plot zur Visualisierung von Datenverteilungen kennen.
- in Calc (bzw. MS Excel) eigene Berechnungen in ausgewählten Zellen durchführen können.
- eine deskriptive Statistik für diesen Datensatz mittels built-in Funktionen und Pivottabelle in Calc berechnen können.
Was ist die deskriptive Statistik?
- Wird auch beschreibende oder empirische Statistik genannt.
- Zur “Vereinfachung” der Datenpunkte in wenige zusammenfassende Merkmale.
- Hilft den originalen Datensatz leichter zu verstehen.
- Gehört zur Datenexploration. Sie sollte also IMMER nach der Probennahme gemacht werden und bevor eine Datenanalyse stattfindet!
- Unterscheidet 2 Typen.
2 Typen der deskriptiven Statistik
Numerisch
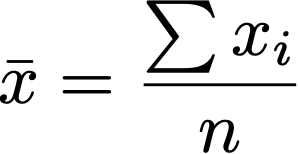
- Aussage über Zentriertheit und Streuung der Werte.
Grafisch
![]()
- Aussage über die Verteilung der Werte.
- Erkennung von Mustern: Unterschiede, Anteile, Beziehungen, Trends, Hierarchien
- Grafiken sind für die Mustererkennung geeigneter, am besten aber immer beides anwenden.
Statistik-Software
Beispiel einer automatischen Zusammenfassung eines Statistik-Programms:
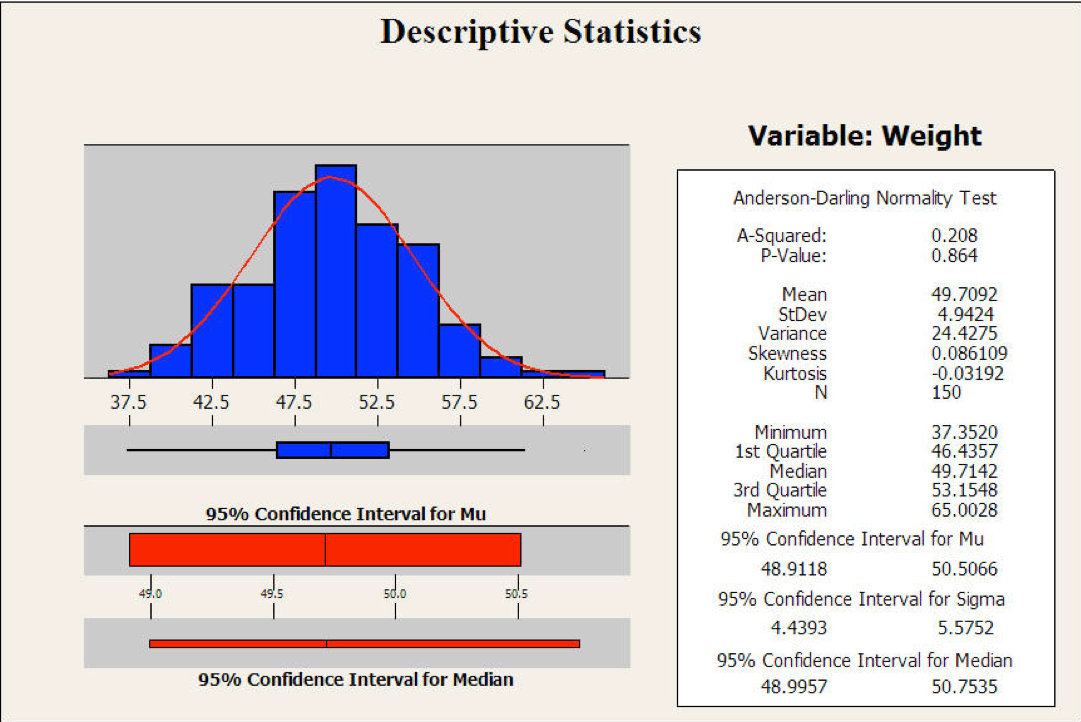
Anwendungsbeispiel
COVID-19 Dashboards
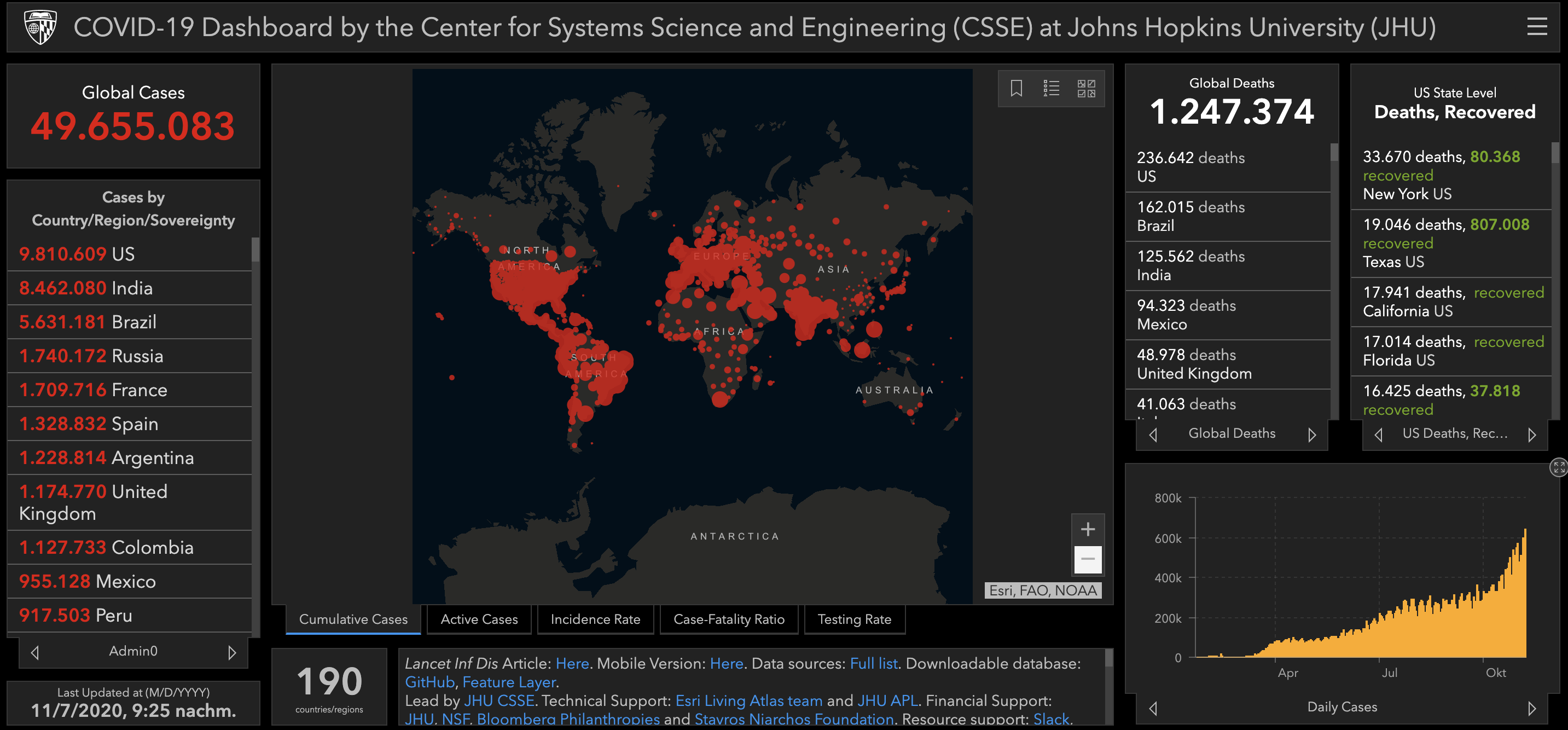
Screenshot des COVID-19 Dashboard des CSSE der John Hopkins Universität (Stand 7.11.2020). Link: https://coronavirus.jhu.edu/map.html
Numerische deskriptive Statistik
Ein wichtiges Grundkonzept
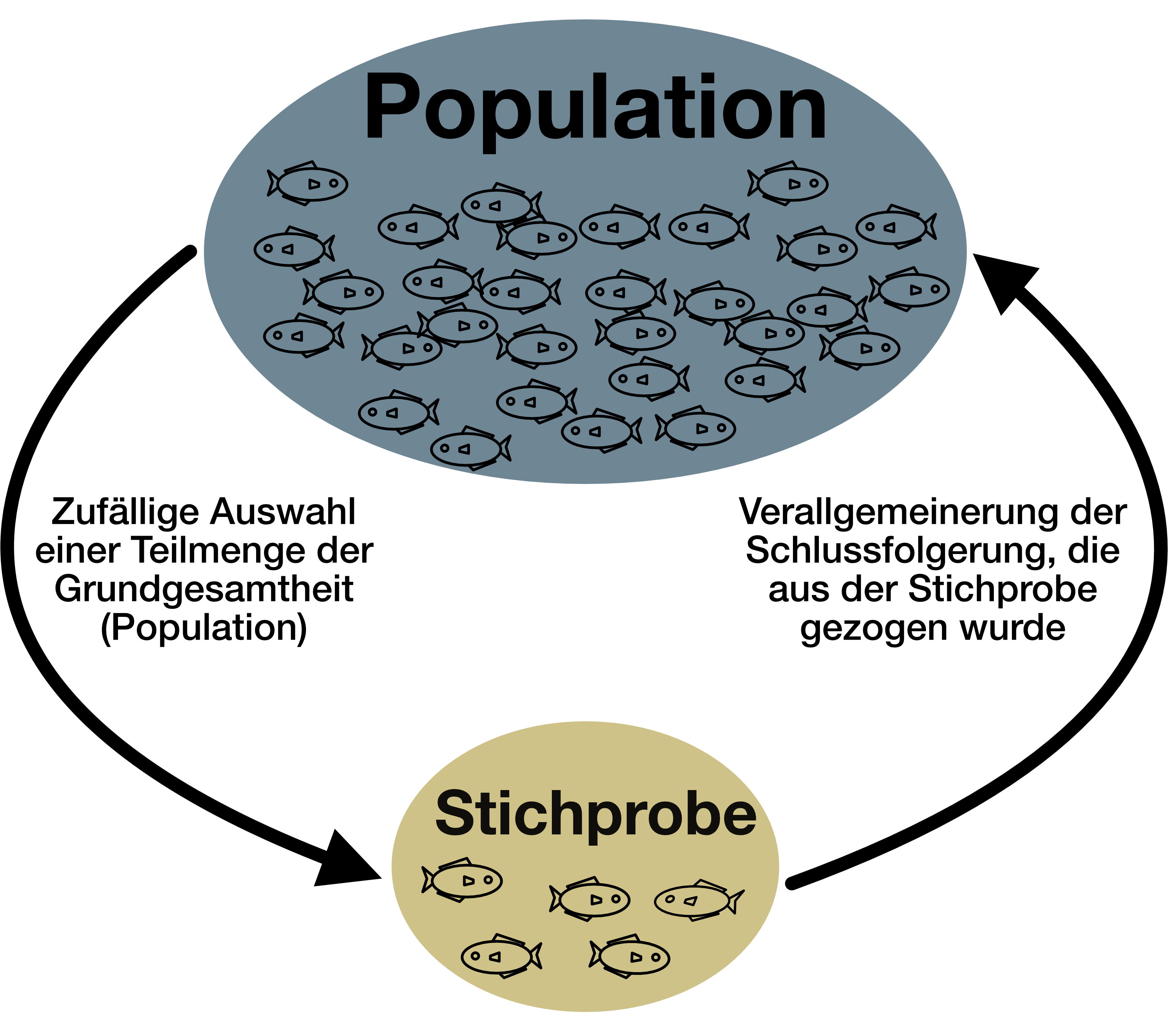
Definitionen
Was sind Parameter, Schätzwerte und Stichprobenverteilungen?
![]()
Parameter
- Ein Merkmal welches die Grundgesamtheit beschreibt.
- Allerdings selten möglich, die vollständige Grundgesamtheit zu messen.
- Verwendung griechischer Buchstaben: \mu, \sigma^{2}
Parameterschätzwerte bzw. Stichprobenstatistik
- Zusammenfassung von Informationen über einen Parameter, der aus einer Stichprobe gewonnen wurde.
- Werte variieren zufällig von einer Zufallsstichprobe zur nächsten → daher stellt die Statistik eine Zufallsmenge (Variable) dar.
- Verwendung lateinischer Buchstaben: z.B. \bar{x}, s^2
Stichprobenverteilungen
- Die Wahrscheinlichkeitsverteilung dieser Zufallsvariable.
- Sie ist wichtig, weil sie es ermöglicht, auf der Grundlage einer Zufallsstichprobe Rückschlüsse über den entsprechenden Parameter der Grundgesamtheit zu ziehen.
Lage- vs. Streuungsparameter/-maße
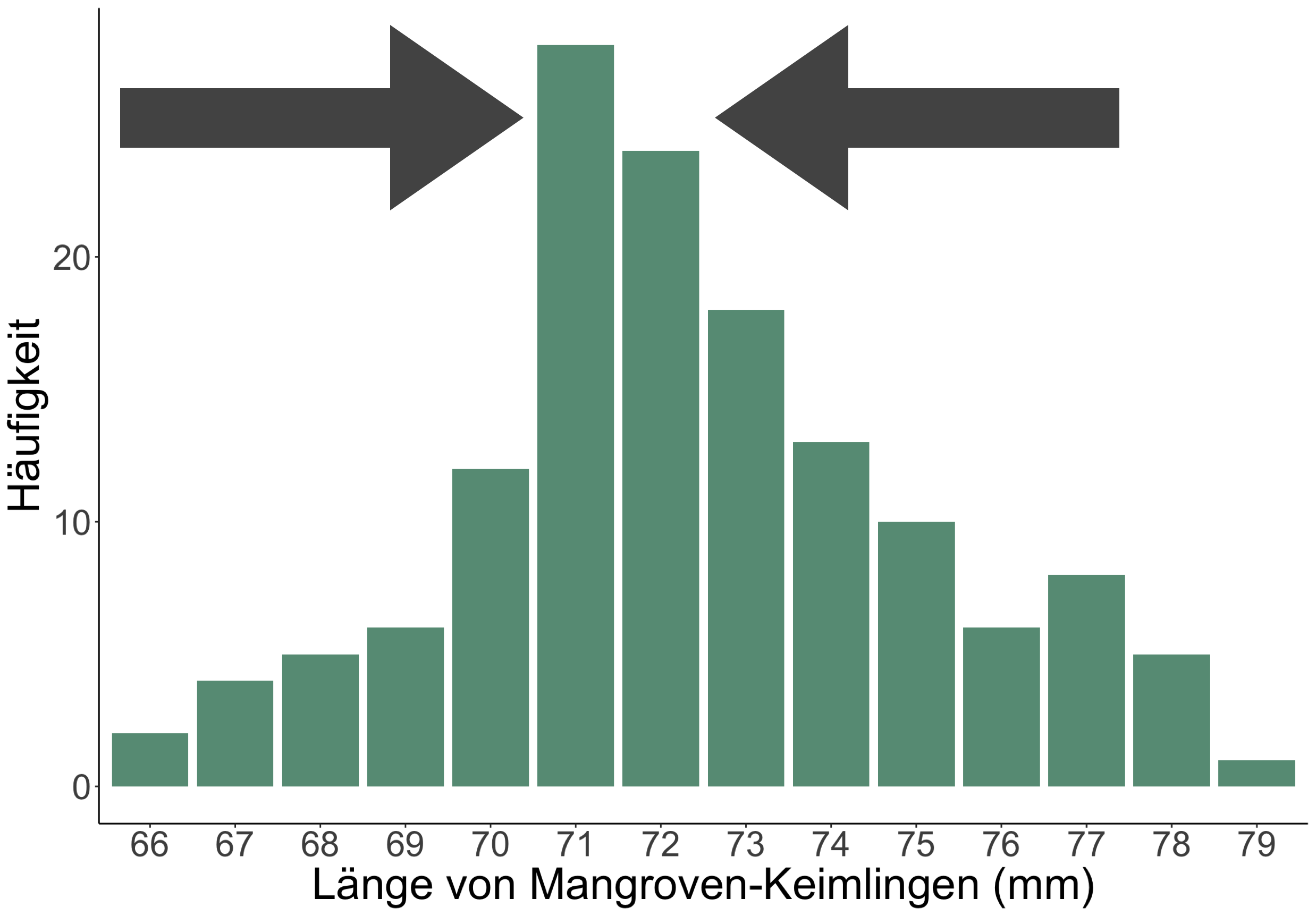
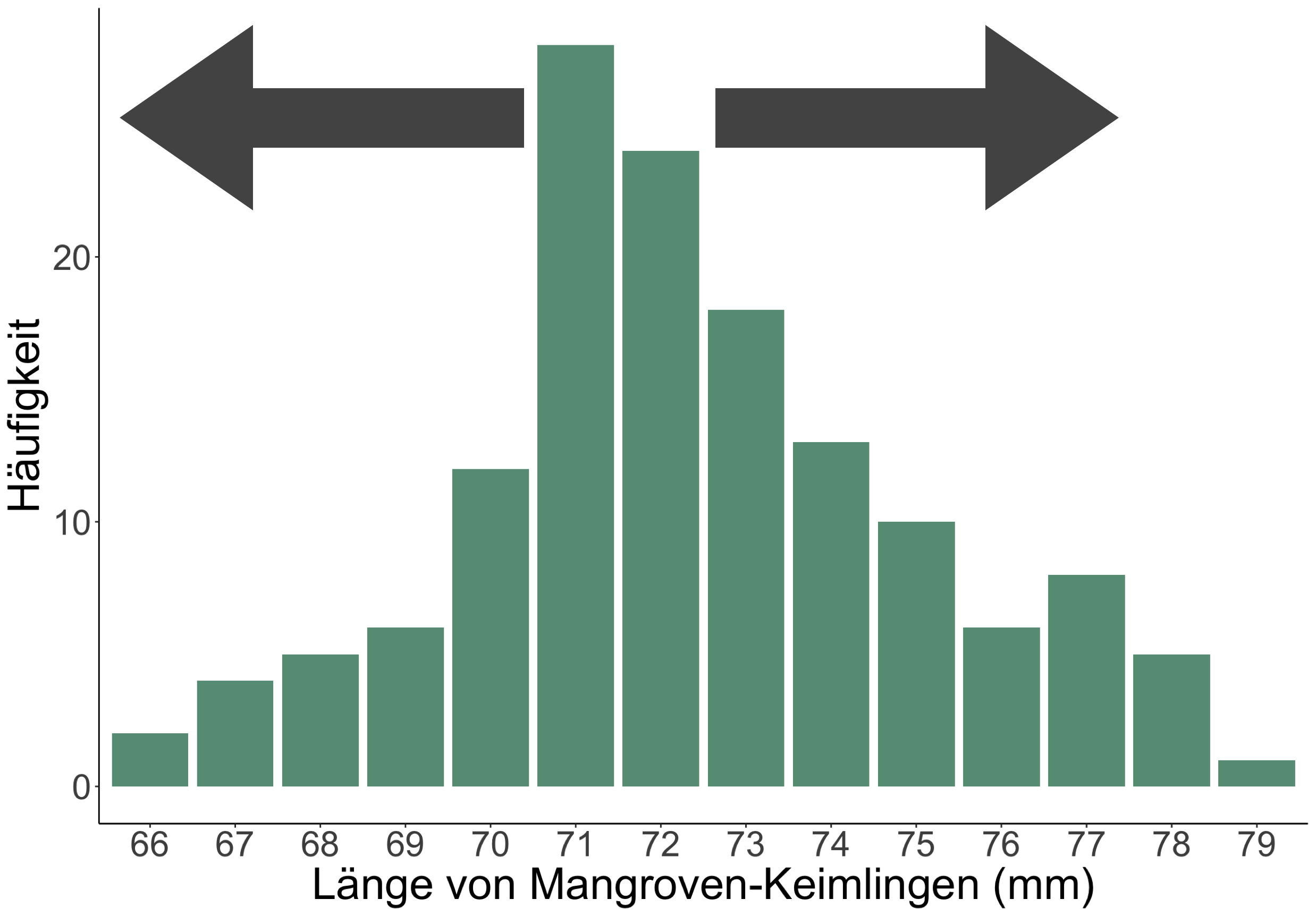
Ein Beispiel aus den Tropen
Länge von Mangroven-Keimlingen
- Die Triebe wuchsen aus Samen heran, die alle zum gleichen Zeitpunkt gepflanzt wurden.
- Spross-/ Trieblänge in mm
- N = 142
- Häufigkeitsverteilung (frequency distribution)

Bildquelle: www.pixabay.com (lizensiert unter CCO 1.0)
Lagemaß: MODALWERT

- Der Modalwert ist der am häufigsten auftretende Wert in einer Verteilung.
- Es ist die einzige Messgröße der Zentriertheit, welche bei nominalen Daten verwendet werden kann.
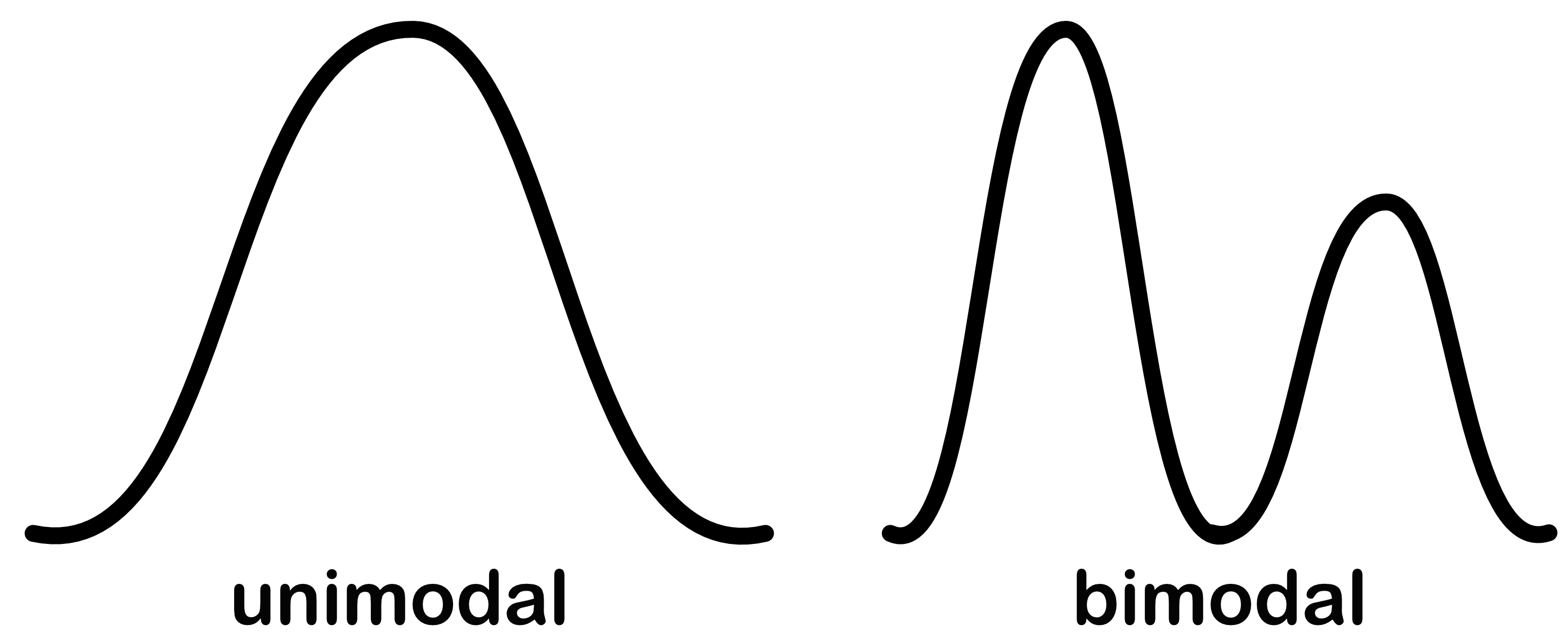
Lagemaß: MODALWERT | Beispiel
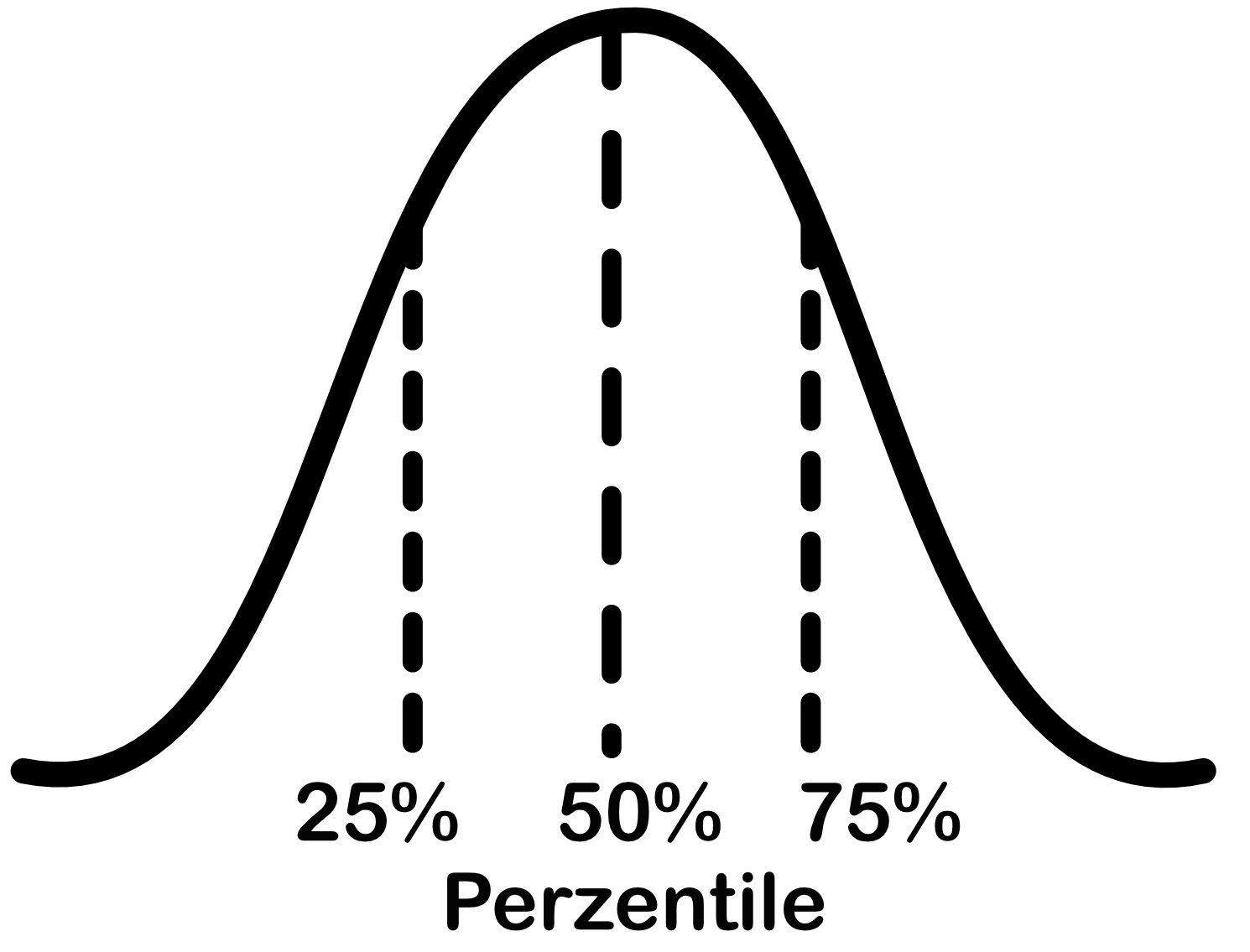
Lagemaß: MEDIAN

- = Die Mitte einer Verteilung.
- Die Hälfte der Werte liegt oberhalb dieses Wertes, die andere Hälfte darunter.
- Wird auch als 50%-Perzentil bezeichnet.
- Kann auch bei ordinalen Daten verwendet werden.
Lagemaß: MITTELWERT

Arithmetischer Mittelwert
\bar{x} = \frac{\sum{x_{i}}}{n}
- Häufig als Mittelwert (‘mean’) oder Durchschnitt (‘average’) bezeichnet; dabei sollte man sehr genau sein, um von den anderen Mittelwerten unterscheiden zu können.
- Parameter: \mu
- Stichprobenstatistik: \bar{x}
Gewichteter Mittelwert
\bar{x} = \frac{\sum{w_{i}*x_{i}}}{\sum{w_{i}}}
- Jedem Datenpunkt x_{i} ist eine Gewichtung w_{i} zugeordnet.
- Weitere: geometrischer Mittelwert, harmonischer Mittelwert, getrimmter Mittelwert
Die 3 Lagemaße im Vergleich | 1

Symmetrische Verteilung - Keimlinge
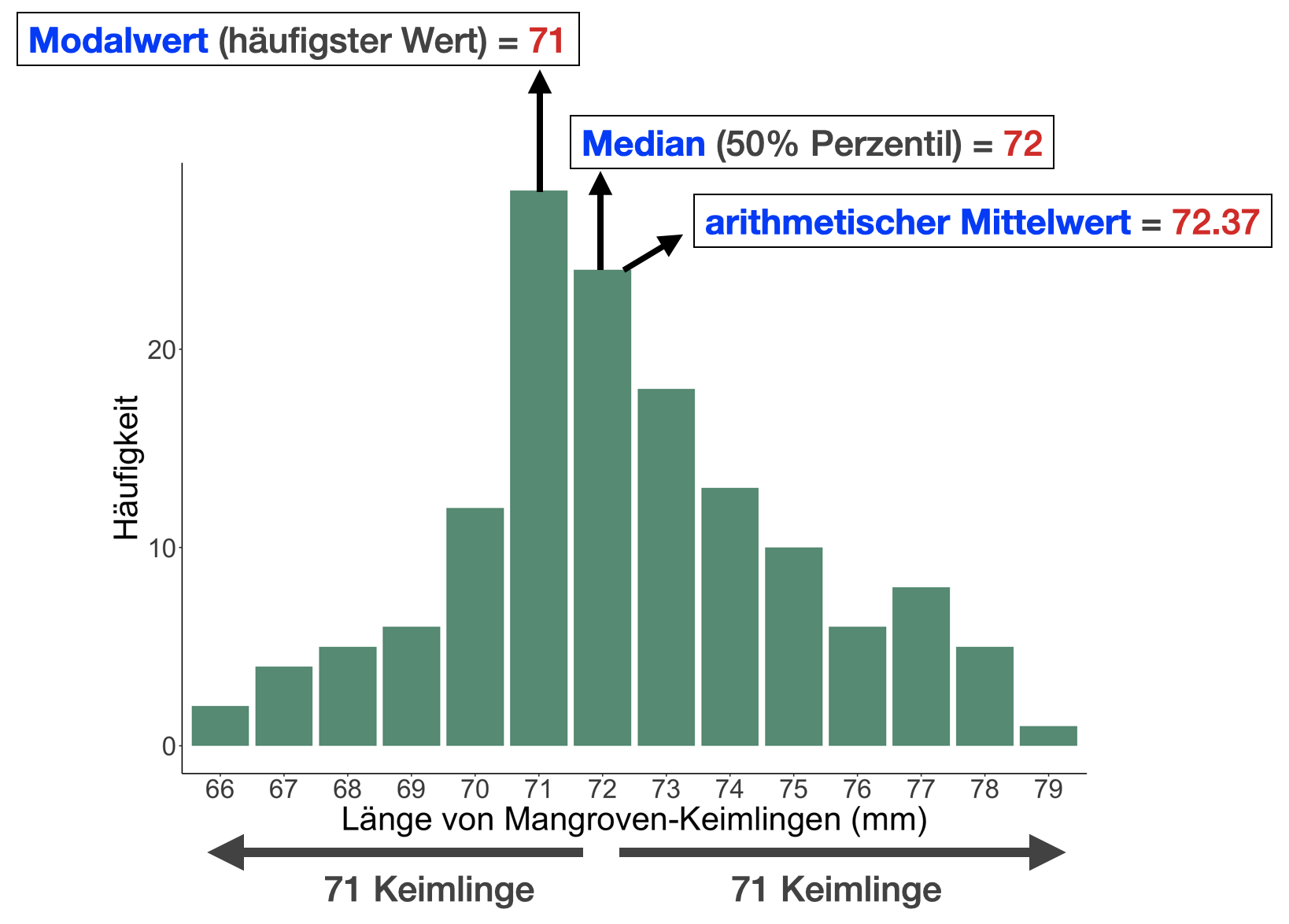
Die 3 Lagemaße im Vergleich | 2
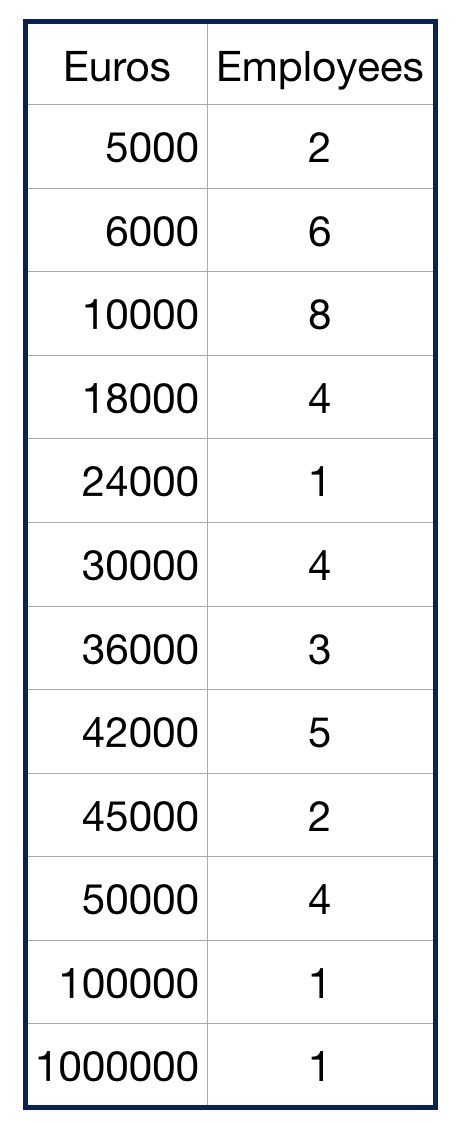
Asymmetrische Verteilung - Gehälter
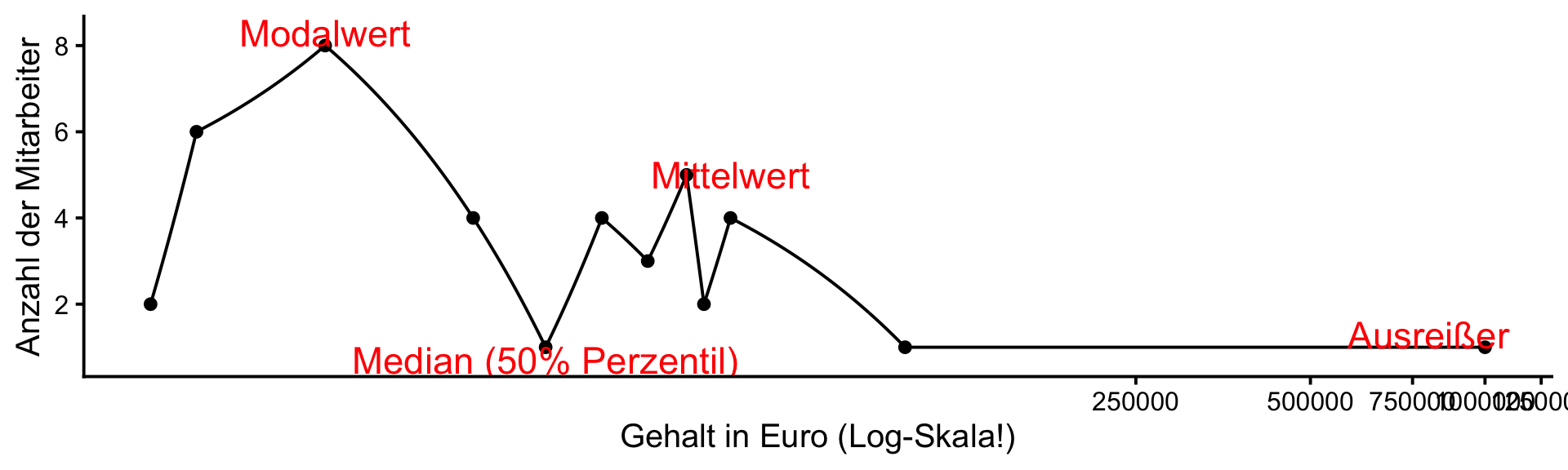
- Der arithmetische Mittelwert kann ein gutes Maß sein, um grob eine symmetrische Verteilung einschätzen zu können.
- Bei einer schiefen Verteilung (‘skewed’) kann er aber auch irreführend sein, da die Verteilung sehr stark von Extremwerten beeinflusst werden kann.
Streuungsparameter bzw. -maße

- auch Dispersionsmaße genannt (Englisch: dispersion, variability, scatter, spread)
- Wichtigste Parameter:
- Variationsbreite oder Spannweite: R=x_{max}-x_{min}
- Varianz
- Standardabweichung
- Standardfehler
- Varianzkoeffizient
Streuungsmaß: VARIANZ

- Parameter \sigma^{2}, Stichprobenstatistik s^{2}
- Wird am häufigsten verwendet.
- Ist eine Messgröße für die gesamte Variabilität.
- Ist weniger sensitiv gegenüber extremen Werten.
- Ist hilfreich bei der Beurteilung der Datenqualität.
Streuungsmaß: VARIANZ | in der Natur

Streuungsmaß: VARIANZ | MSS

- Die Varianz stellt die mittlere Summe der Quadrate der Abweichungen aller Einzelwerte vom Mittelwert (=Residuen) dar.
- Im Englischen: ‘Mean Sum of Squares’ (MSS)
- Die Summe der Residuen ist gleich null → deshalb die Quadrierung!
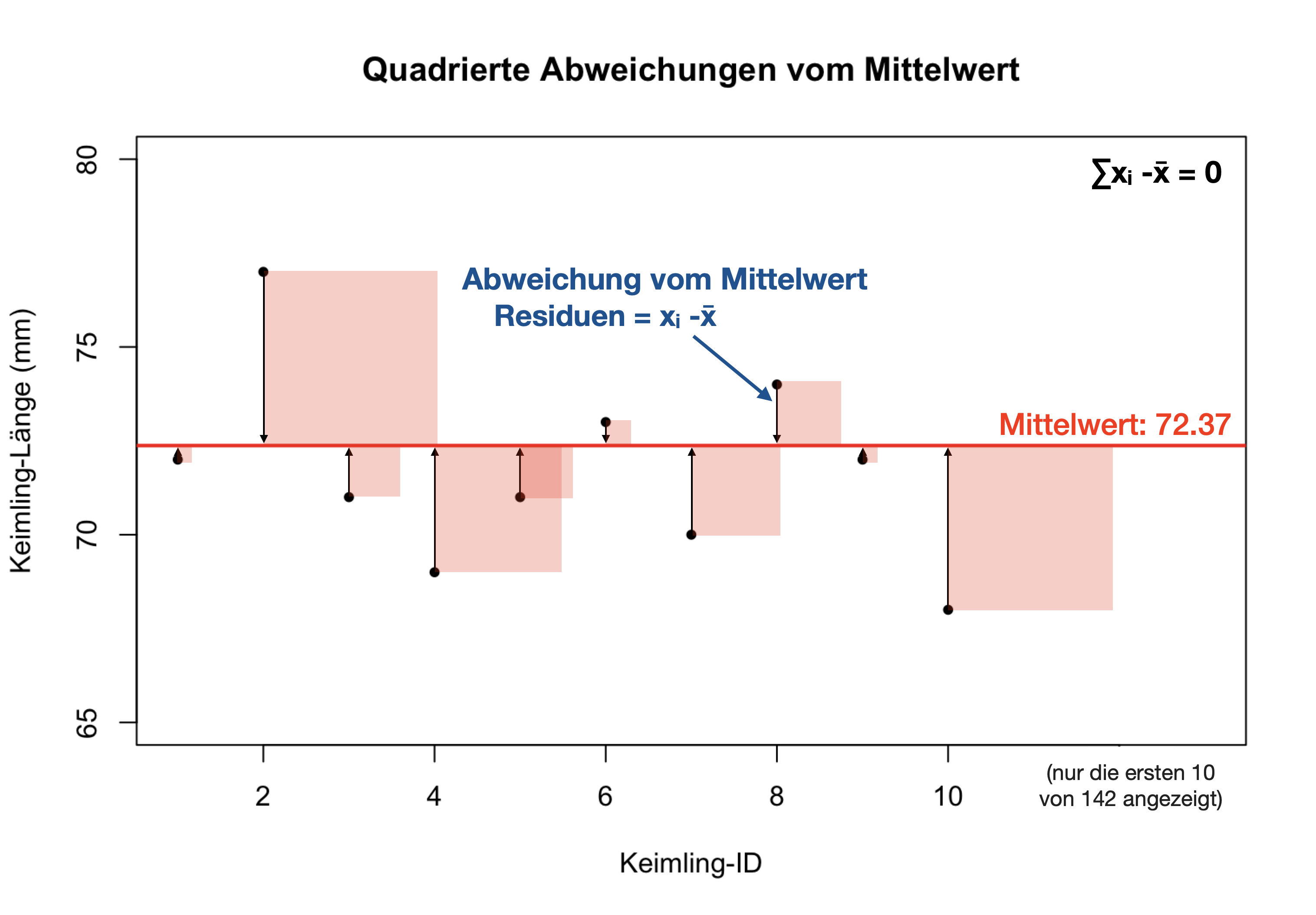
Streuungsmaß: VARIANZ | Gleichung
s^{2} = \frac{\sum\limits_{i=1}^{n} \left(x_{i} - \bar{x}\right)^{2}} {n-1} = \frac{SS}{df}
x_i = die i-te Beobachtung von x
\bar{x} = der Stichprobenmittelwert
n = die Stichprobenzahl
- Wir wollen nicht, dass die Varianz von der Probengröße abhängig ist, deshalb ist die offensichtliche Lösung, durch die Anzahl der Proben zu dividieren um die mittlere, quadrierte Abweichung zu erhalten.
- Aber wozu dann n-1 bzw. was ist df?
Streuungsmaß: VARIANZ | Freiheitsgrade
- Das n-1 in der Gleichung stellt die Anzahl der sogenannten Freiheitsgrade (‘degrees of freedom’= df) dar:
- df = n-p → mit p = Anzahl der geschätzten Parameter für die Daten
Beispiel
![]()
Eine Probe hat 5 Zahlen und einen Mittelwert von 4
→ Die Summe muss 20 sein.
Wenn die ersten 4 Zahlen 1, 1, 4, und 10 sind, dann muss die letzte Zahl 4 sein;
→ wir haben 4 Freiheitsgrade für 5 Zahlen.
Streuungsmaß: STANDARDABWEICHUNG
- Die Standardabweichung \sigma bzw. s (‘standard deviation’, SD) ist einfach die Quadratwurzel der Varianz.
- Sie wird somit in der gleichen Einheit wie die Daten ausgedrückt.
- Wird typischerweise für Fehlerbalken in Graphen verwendet.
- Wenn die Daten normal verteilt sind,
- fallen 68% aller Messungen innerhalb einer SD vom Mittelwert.
- fallen 95% aller Messungen innerhalb zwei SD vom Mittelwert.
s = \sqrt{s^2}
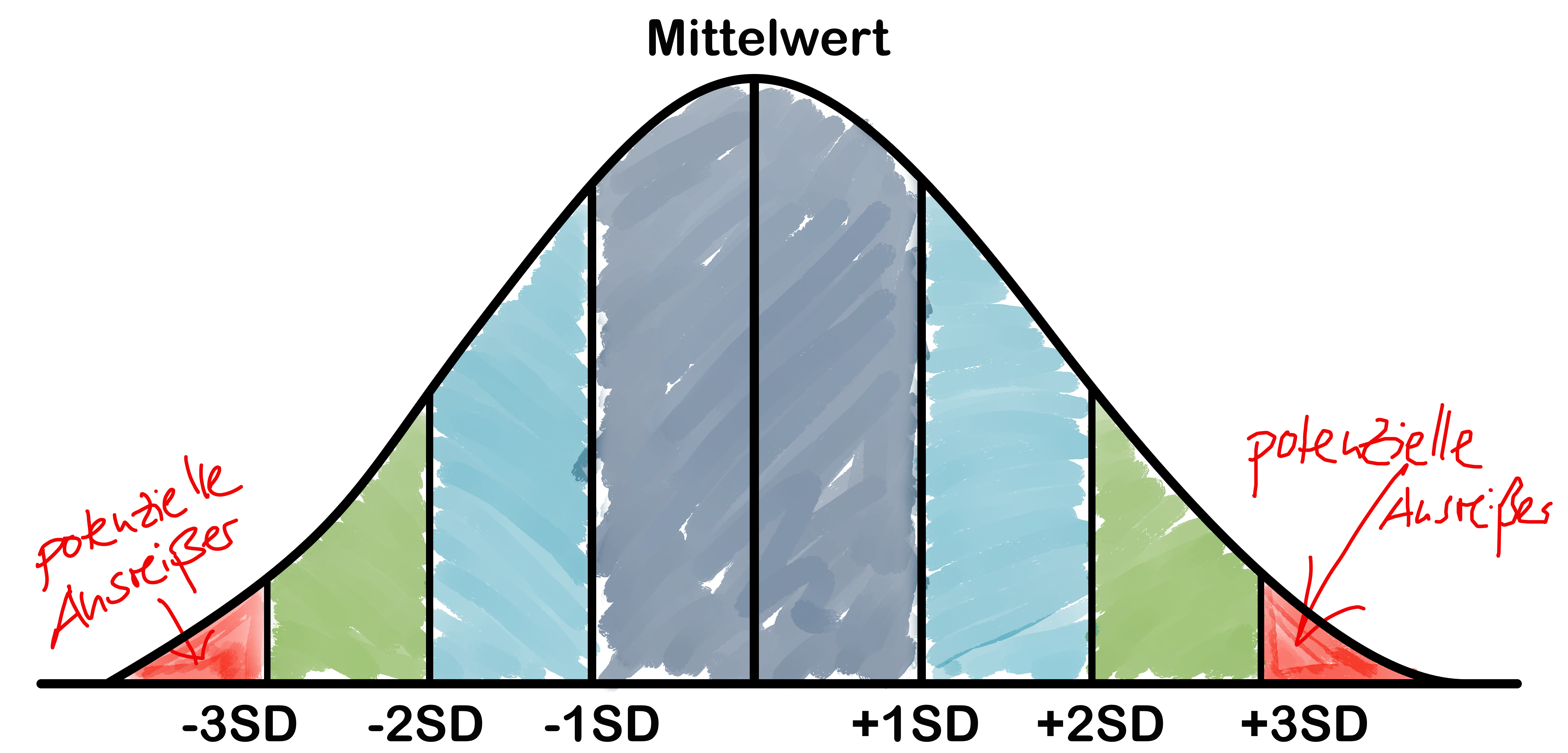
Streuungsmaß: STANDARDFEHLER

- Der Standardfehler s_{\bar{x}} der Stichprobe (‘standard error’, SE) normalisiert die Standardabweichung durch die Quadratwurzel der Probenanzahl n
- Je größer die Probenanzahl n, desto größer ist s^{2} und s
- → SE gibt eine Einschätzung der Variabilität unabhängig von der Probenanzahl.
- Je größer n, desto kleiner SE.
- Bei Gruppenvergleichen mit unterschiedlicher Probenanzahl sollte immer SE verwendet werden!
s_{\bar{x}} = \sqrt\frac{s^2}{{n}} = \frac{s}{\sqrt{n}}
Streuungsmaß: VARIATIONSKOEFFIZIENT
- Im Englischen ‘Coefficient of variation’ (CV) genannt.
- Definiert als das Verhältnis von Standardabweichung und Mittelwert (häufig in Prozent ausgedrückt).
- Erlaubt den Vergleich der Varianz von Populationen, die unterschiedliche Mittelwerte haben.
- Tendiert dazu bei kleiner Probengröße verzerrt zu sein (bias).
CV = \frac{s}{\bar{x}}

Bildquelle: McClain et al. 2015, DOI: 10.7717/peerj.715
Your turn …
![]()
01:00
Quiz 1 | Finden Sie den Modalwert
![]()
Folgende Werte wurden gemessen:
51 51 54 54 54 54 57 57 57 65 75 75 75 75 75 75 75 75 75 75 76 77 77 77 83 83 95 95 95 95 96 96 96 96 96
Quiz 2 | Reihenfolge der Lagemaße
![]()
Folgende Datenverteilung wurde beobachtet
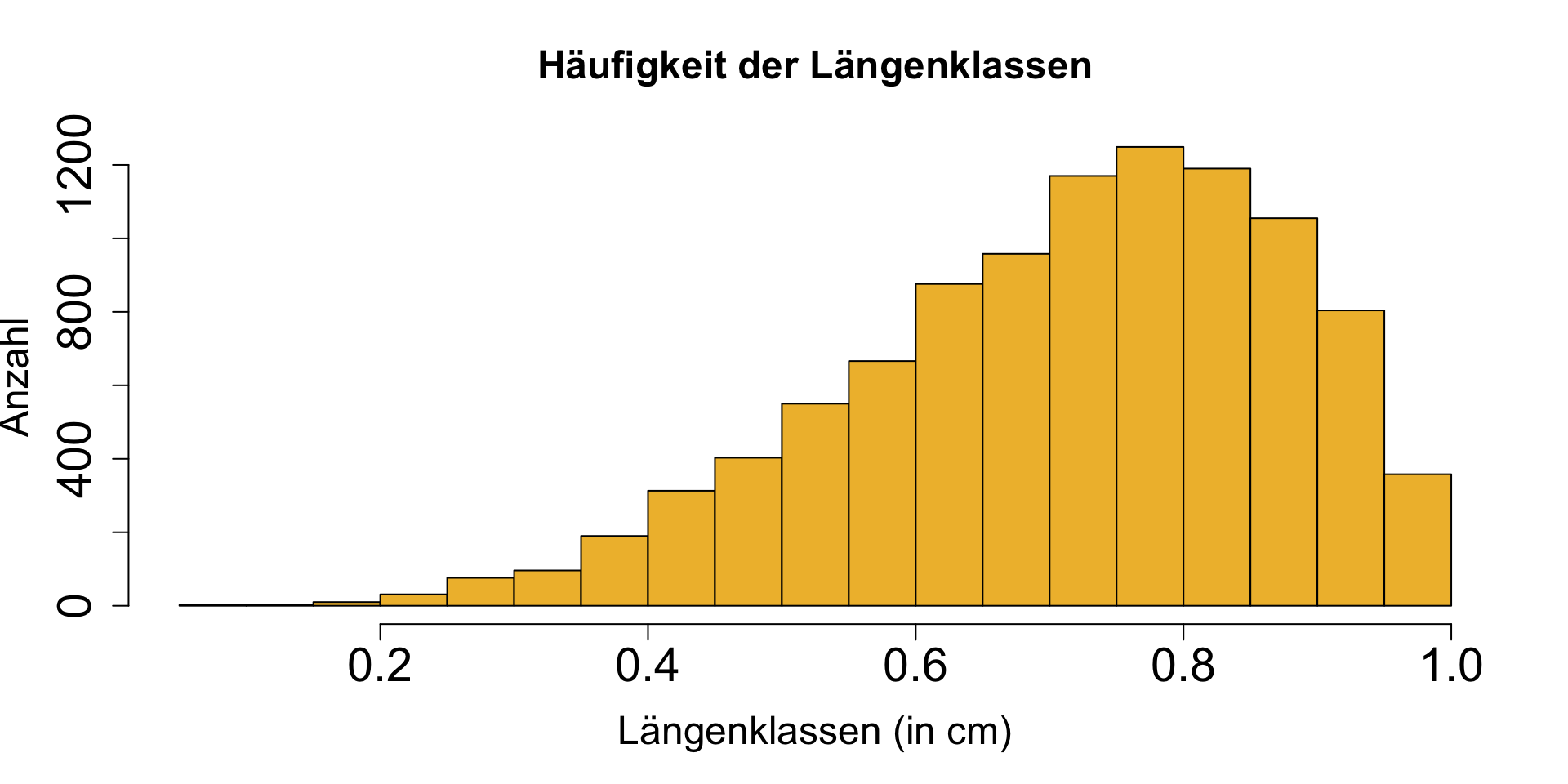
Quiz 3 | Finden Sie die richtige Statistik
![]()
Folgende Gleichungen sind gegeben. Welche Stichprobenstatistik wird jeweils repräsentiert?
\sqrt{\frac{\sum\limits_{i=1}^{n} \left(x_{i} - \bar{x}\right)^{2}} {n-1}}
\frac{\sum{x_{i}}}{n}
Datenverteilung - eine grafische Herangehensweise

Häufigkeitsverteilung

- Ein wichtiger Aspekt der Beschreibung einer Variablen ist die Form ihrer Verteilung → gibt die Häufigkeit von Werten der verschiedenen Wertebereiche der Variable an.
- Typischerweise ist man daran interessiert, wie gut die Verteilung durch die Normalverteilung beschreiben werden kann:
normal verteilt
nicht normal verteilt

Unterscheidet zwischen..

Häufigkeitsverteilung
- Zeigt einfach nur, wie oft ein Wert vorkommt (Ist-Werte)
- = empirische Verteilung, im Englischen frequency distribution
Wahrscheinlichkeitsverteilung
- Zeigt, wie häufig ein Wert hätte vorkommen sollen (Erwartungswerte)
- = theoretische Verteilung, im Englischen probability distribution
Normalverteilung
Die wichtigste Wahrscheinlichkeitsverteilung
Hat 3 Eigenschaften
- Kontinuierliche, symmetrische Verteilung mit mehr Werten in der Mitte als am Rand (tails) → typische Glockenform (bell shape). Spannweite von -∞ bis +∞.
- Die Schiefe (skewness) ist null, da die Verteilung symmetrisch um den Mittelwert liegt.
- Zwei Parameter spezifizieren die Normalverteilung: Mittelwert und Varianz
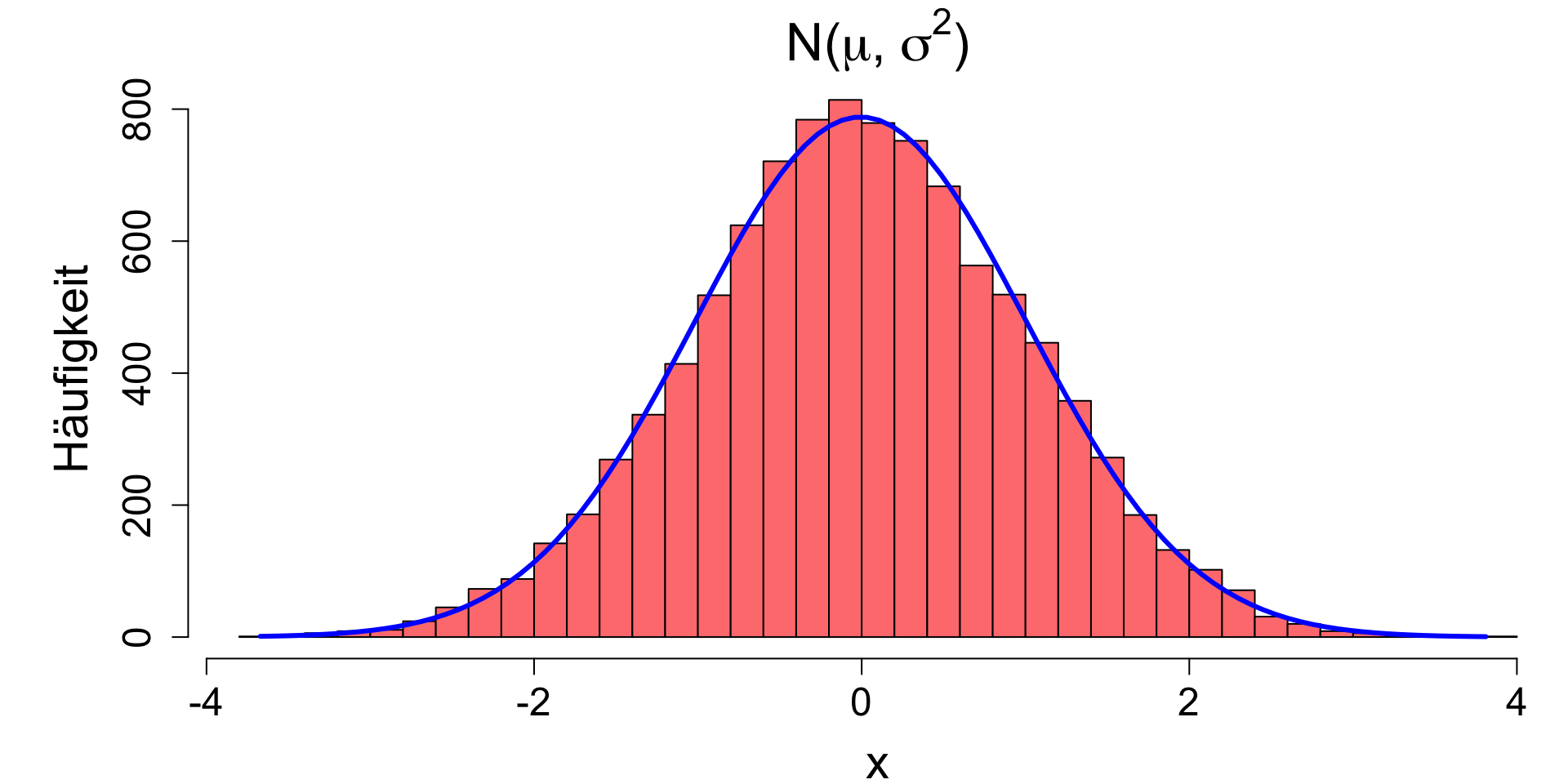
Warum ist das wichtig?
- Viele Methoden basieren auf der Normalverteilung.
- Viele Variablen folgen mit steigender Probenanzahl einer Normalverteilung (zentraler Grenzwertsatz)
Eigenschaften von Verteilungen | 1
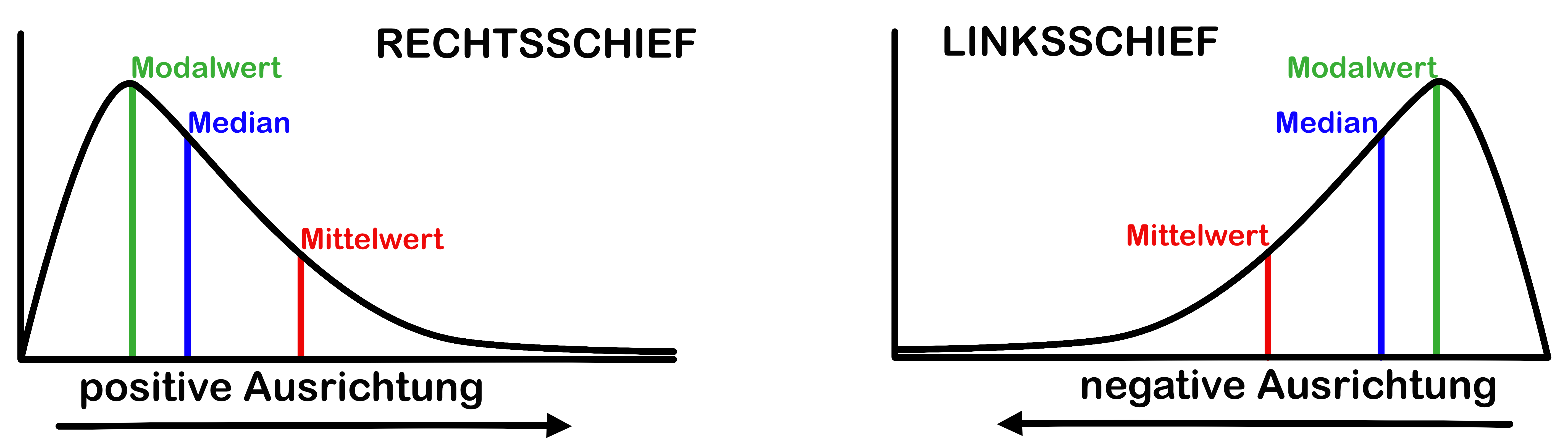
Schiefe (Skewness)
- Eine Verteilung ist schief, wenn ein Ende/Rand (tail) länger ist als das andere.
- Positive Schiefe (\gamma_1>0) kommt häufiger vor (z.B. bei Mengen/Abundanz, Einkommen …).
\gamma_1 = \frac{\frac{1}{n}\sum\limits_{i=1}^{n} \left(x_{i} - \bar{x}\right)^{3}} {(\frac{1}{n}\sum\limits_{i=1}^{n} \left(x_{i} - \bar{x}\right)^{2})^{3/2}}
Eigenschaften von Verteilungen | 2
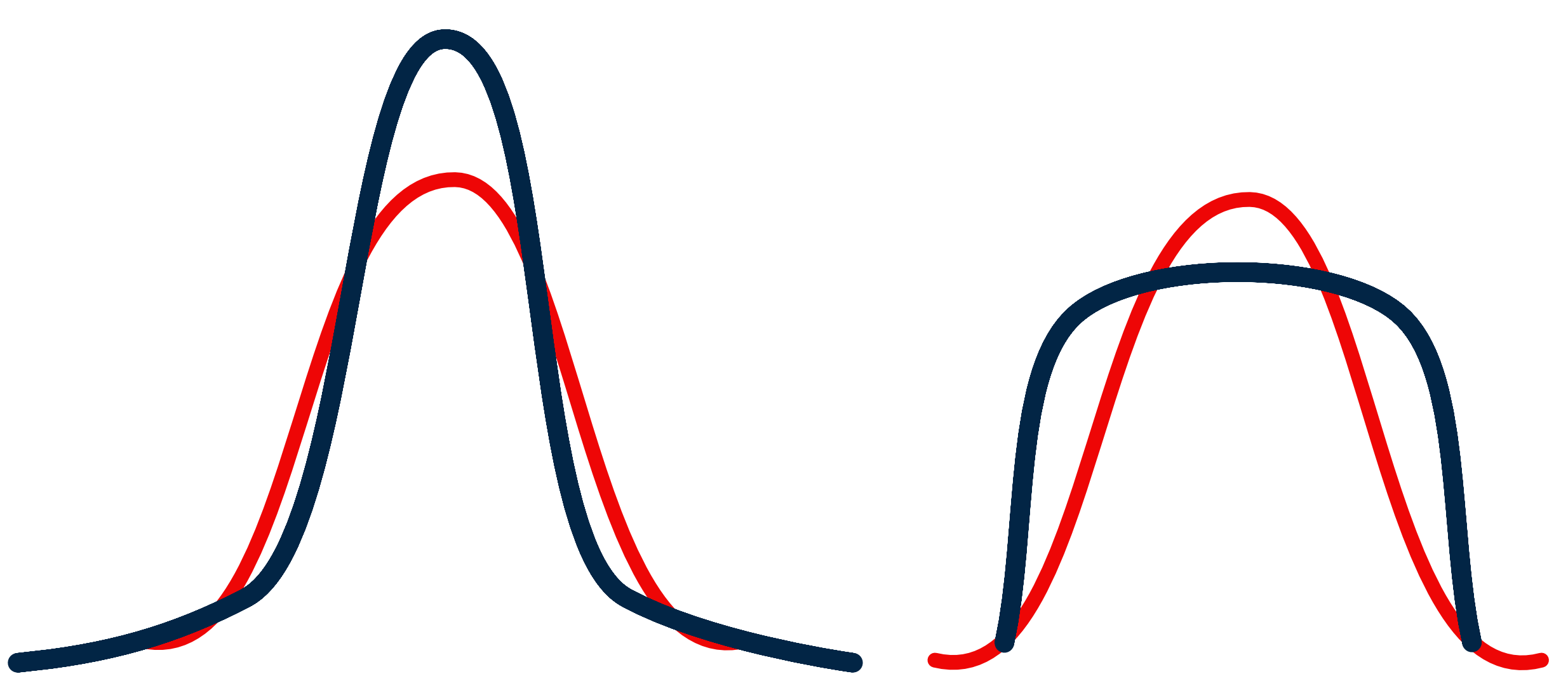
Kurtosis = Wölbung
\gamma_2 = \frac{\frac{1}{n}\sum\limits_{i=1}^{n} \left(x_{i} - \bar{x}\right)^{4}} {(\frac{1}{n}\sum\limits_{i=1}^{n} \left(x_{i} - \bar{x}\right)^{2})^2}
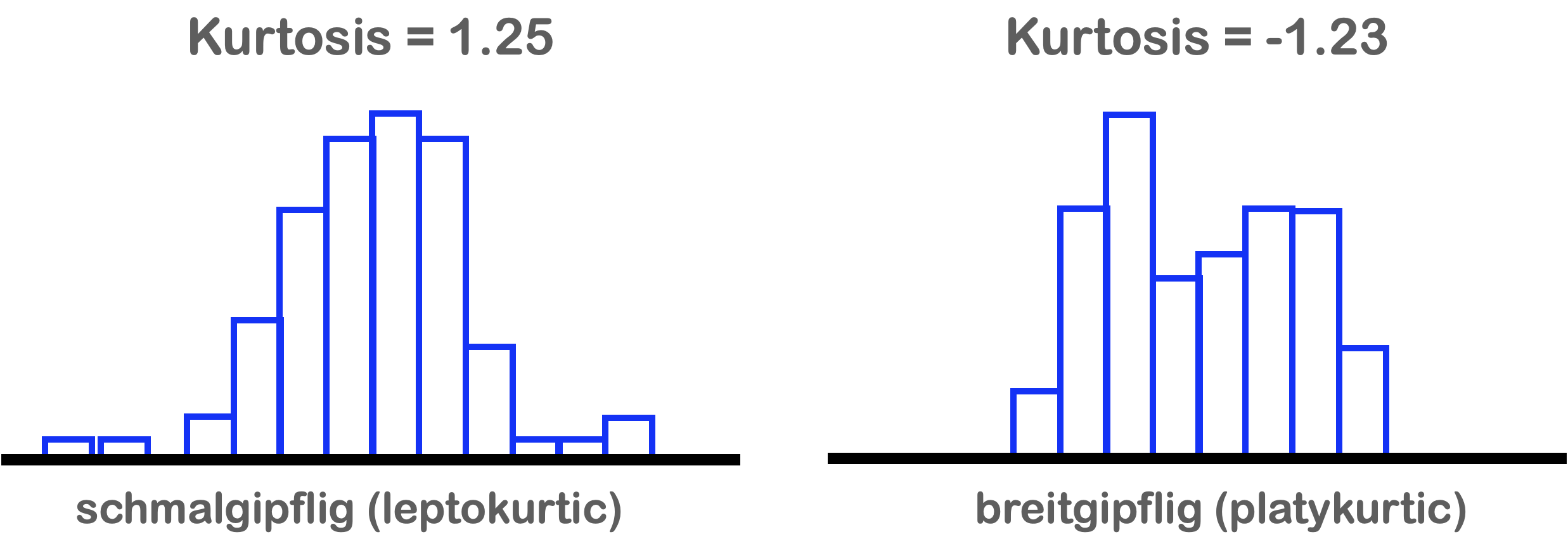
- Basiert auf der Größe des Verteilungsrandes (distribution tail).
- Wird gemessen an der “Spitzigkeit” der Verteilung:
- leptokurtisch (schmalgipflig): relativ lange Enden (\gamma_2 > 0)
- platykurtisch (breitgipflig): kurze Enden (\gamma_2 < 0)
- mesokurtisch (normalgipflig): eine Verteilung mit der gleichen Kurtosis wie die Normalverteilung (\gamma_2 = 0)
Wichtige Grafiken zu Verteilungen

Histogramm | 1
![]()
- Werden verwendet um Häufigkeitsverteilungen von kontinuierlichen Variablen darzustellen und auf Normalverteilung zu prüfen.
- Werte werden in Wertebereichen (sog. bins) gruppiert und anschl. die Häufigkeiten ermittelt
- Die Säulen berühren sich.
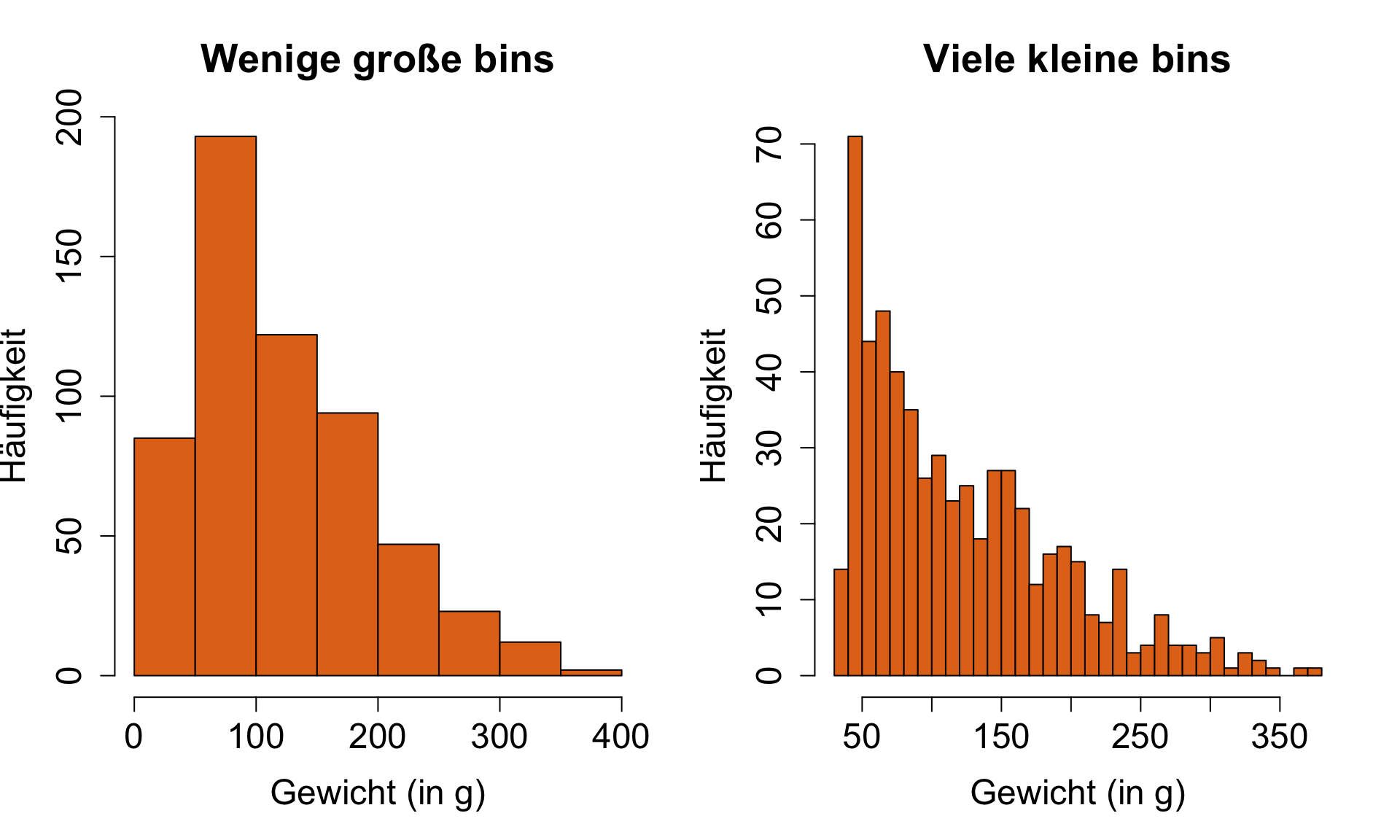
Histogramm | 2
![]()
Einfluss unterschiedlicher Anzahl an ‘bins’
Säulendiagramm (‘column chart’)
![]()
- Werden verwendet um Häufigkeitsverteilungen von kategorialen oder diskreten Variablen darzustellen.
- Die Säulen berühren sich nicht, denn es gibt keine “Zwischenwerte”.
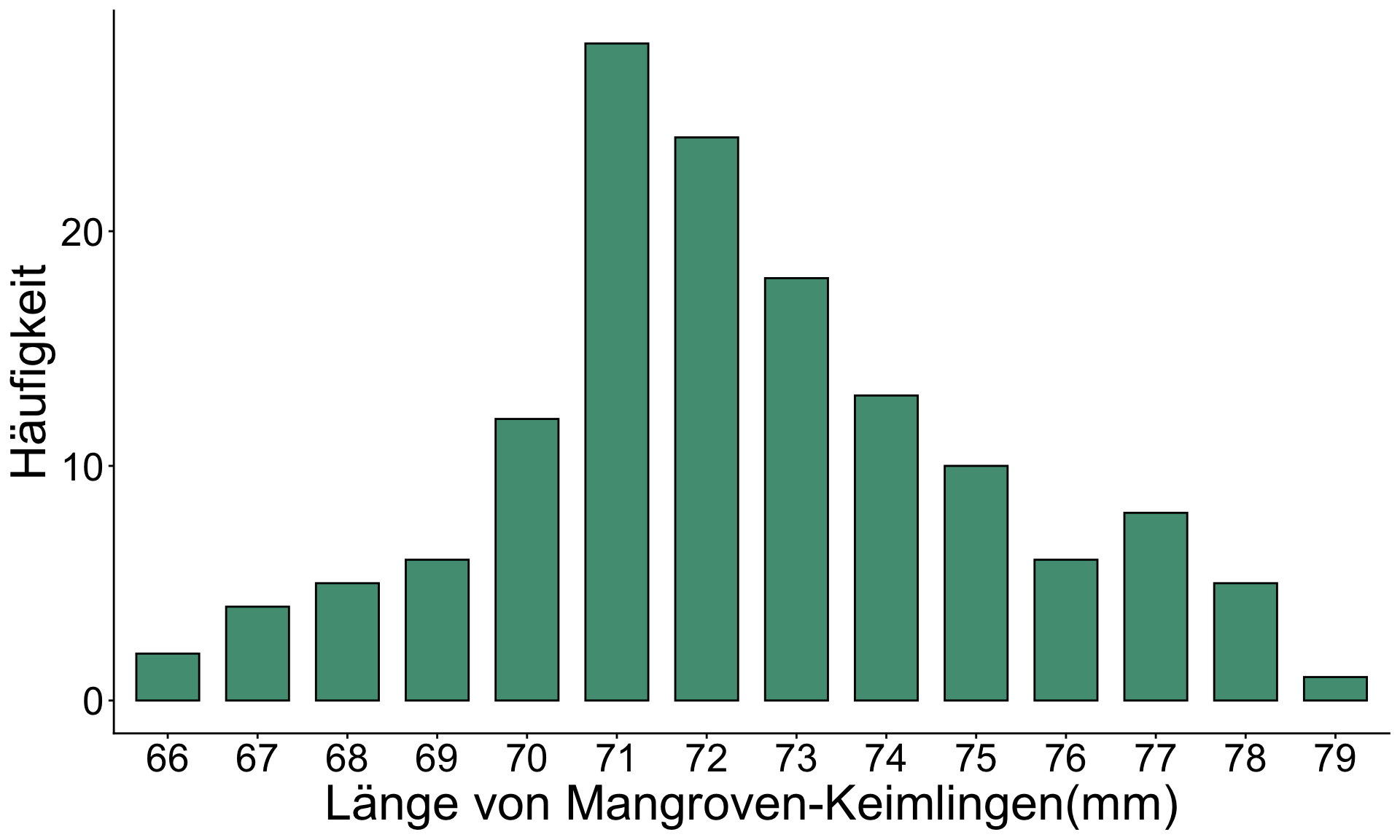

Balkendiagramm (‘bar chart’)
![]()
- Ist dem Säulendiagramm sehr ähnlich, allerdings sind die Achsen vertauscht:
- Aus den vertikalen Säulen werden horizontale Balken.
- Es wächst in die Länge und nicht in die Breite.
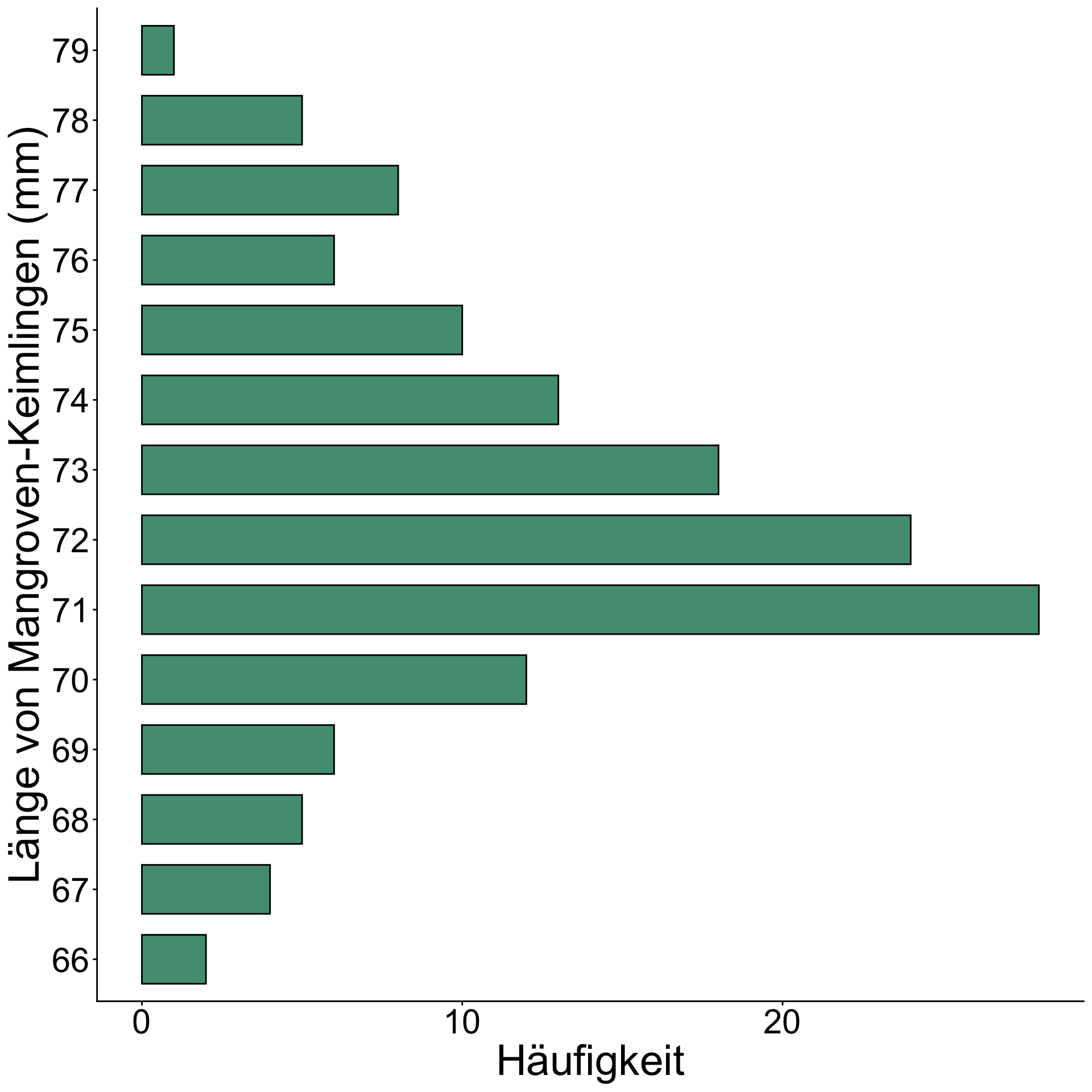

Boxplot| 1
![]()
‘1D’ Boxplot - Verteilung einer Variable
- Visualisiert den Median (2.Quartil) und die 25% und 75% Perzentilen (1. bzw. 3.Quartil) als Streuungsparameter.
- 50% aller Datenpunkte liegen somit innerhalb der Box.
- Die unteren und oberen 25% werden als sog. whisker angezeigt.
- Extremwerte werden durch Punkte dargestellt.
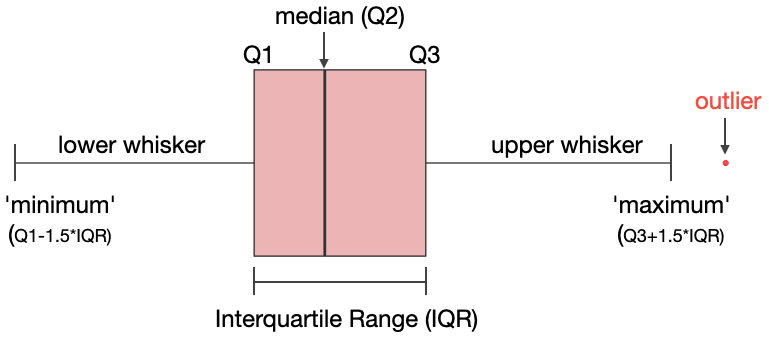
Boxplot| 2
![]()
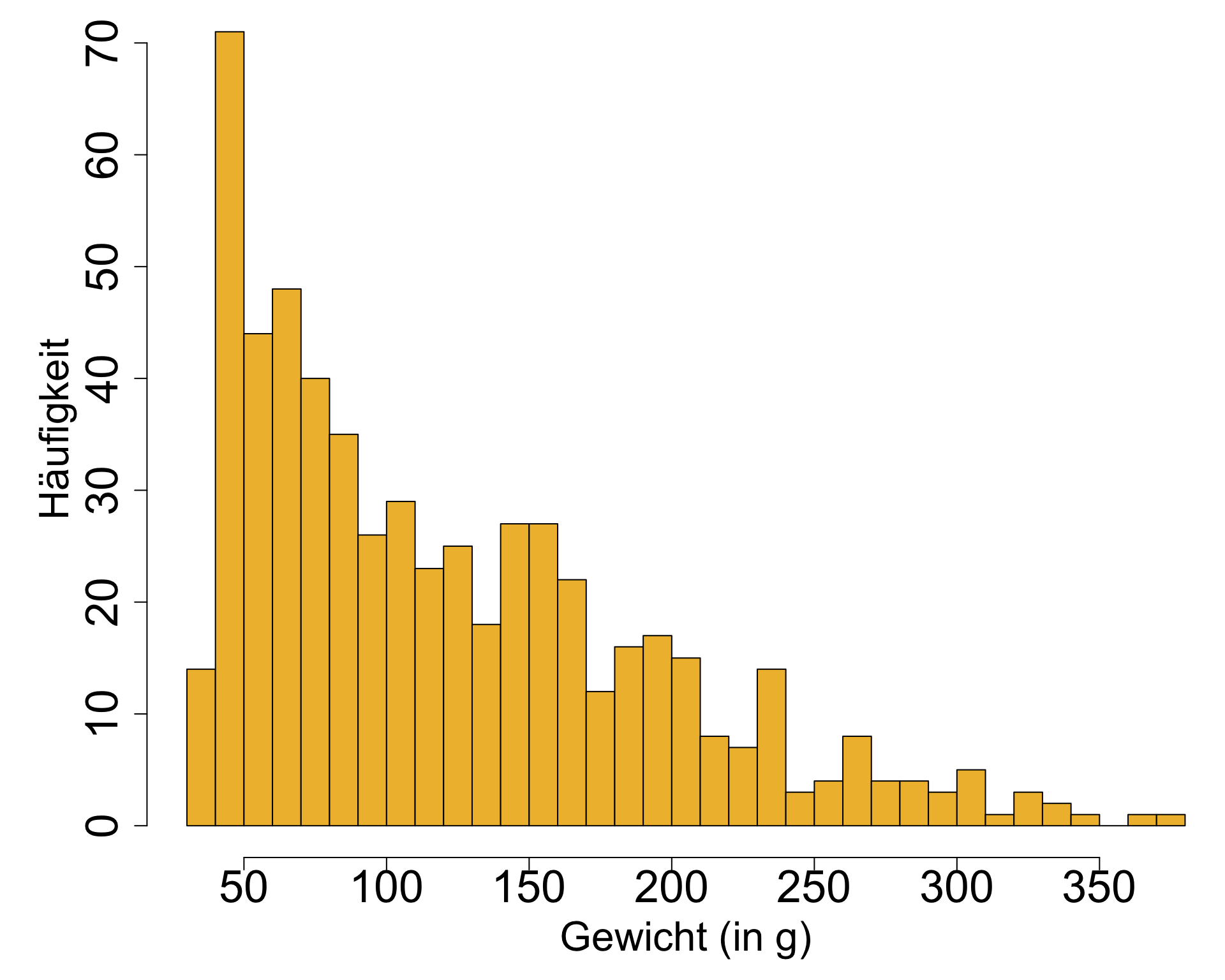
‘1D’ Boxplot - Mangroven-Beispiel
Folgende Fragen lassen sich mit dem Boxplot beantworten:
- Gibt es eine große Streuung?
- Sind die Beobachtungen homogen verteilt (normal und nicht schief), d.h.
- der Median ist mittig in der Box?
- beide whisker sind gleich lang?
- Ist die Verteilung gewölbt (also schmalgipflig-leptocurtic), d.h.
- die whisker sind wesentlich länger als beide Boxhälften?
- Gibt es Ausreißer?


Boxplot| 3
![]()
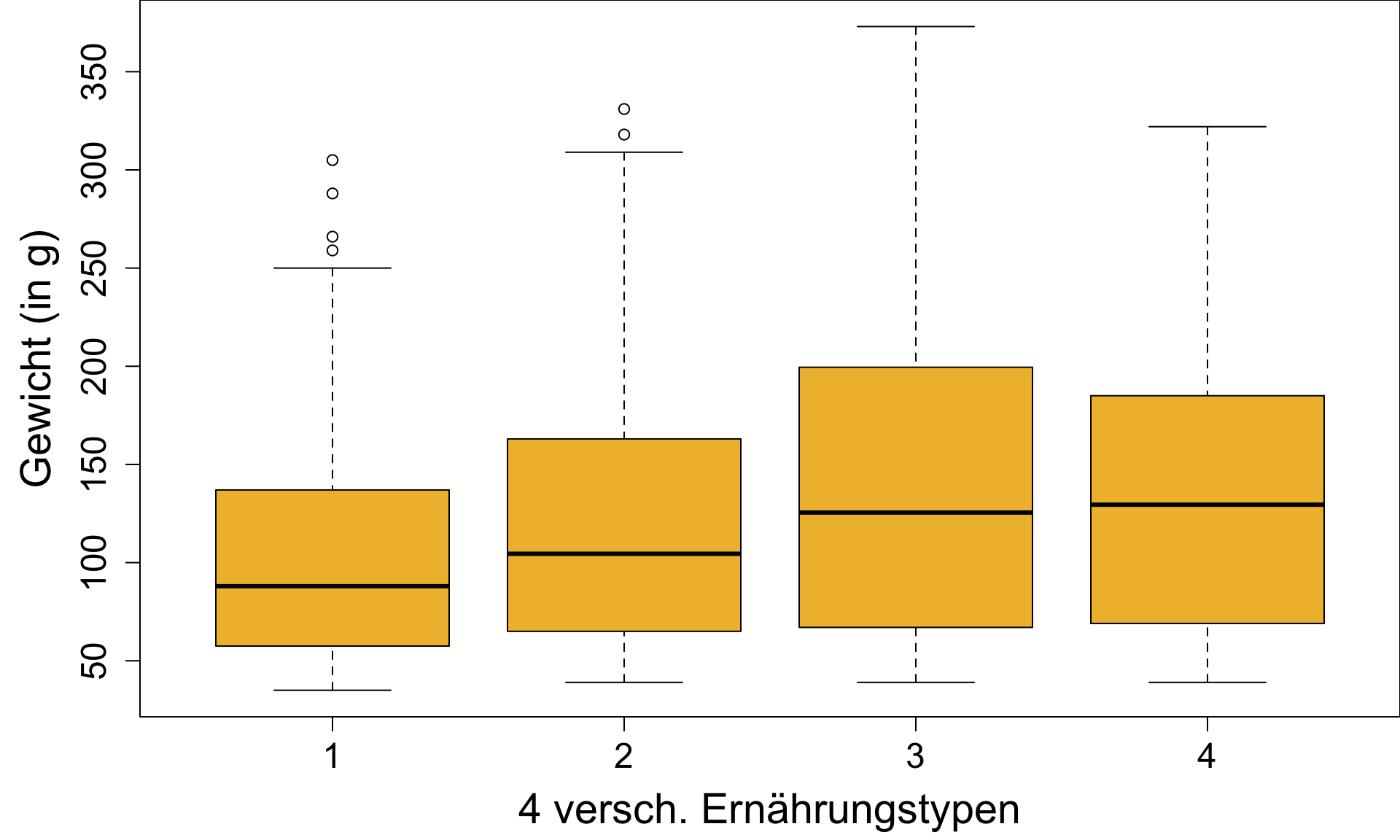
‘2D’ Boxplot zum Gruppenvergleich
Boxplots eignen sich besonders gut, zwei oder mehr Gruppen im Hinblick auf die Verteilung ihres Mittelpunktes und ihrer Variabilität zu vergleichen.
Sie können überprüfen,
- ob es Unterschiede im durchschnittlichen Y-Wert zwischen Gruppen gibt,
- ob sich Varianzen zwischen Gruppen unterscheiden,
- ob individuelle Gruppen normal verteilt sind.
Your turn …
![]()
02:30
Quiz 4 | Schiefe
![]()
Quiz 5 | Kurtosis
![]()
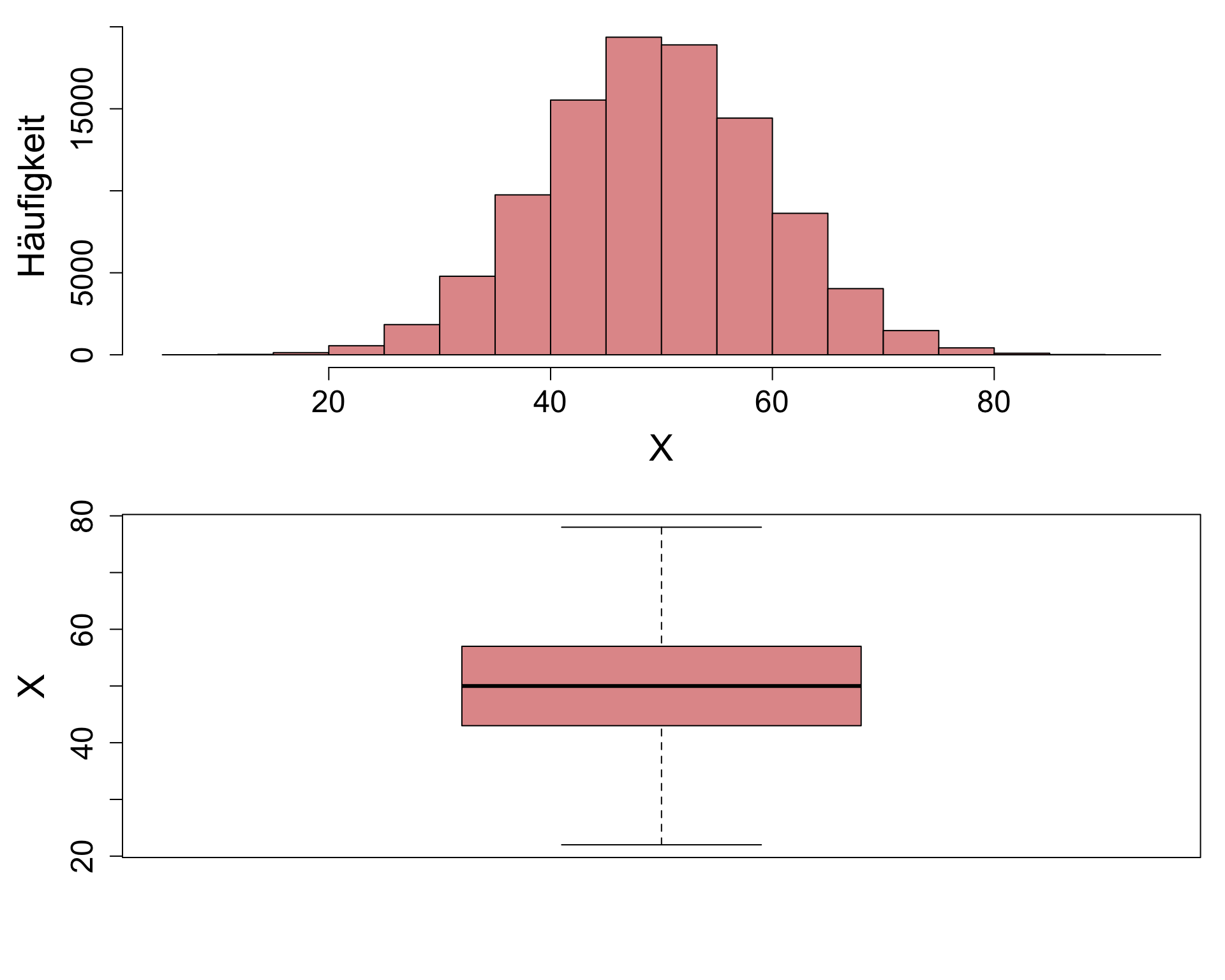
Quiz 6 | Kurtosis
![]()
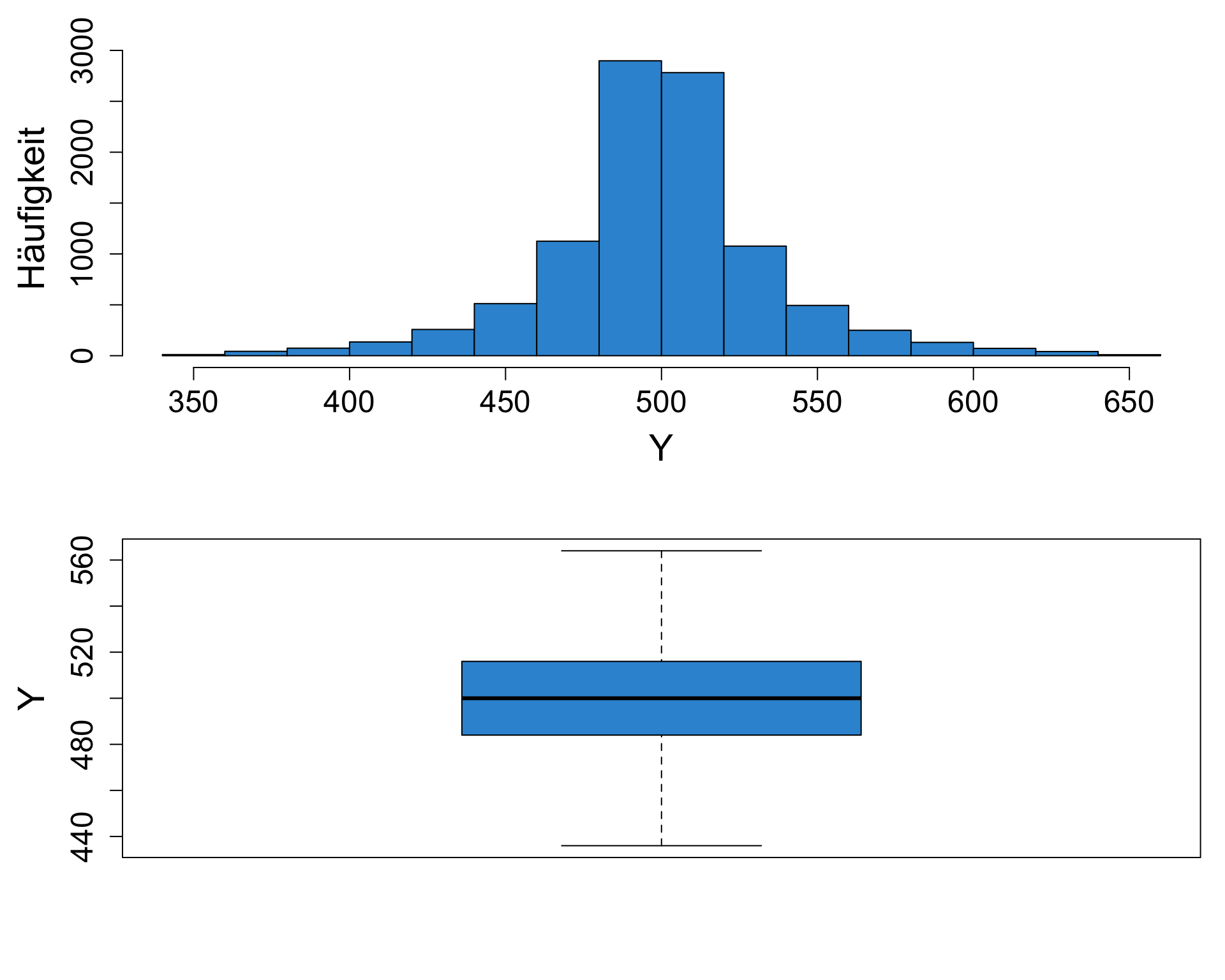
Quiz 7 | Schiefe
![]()
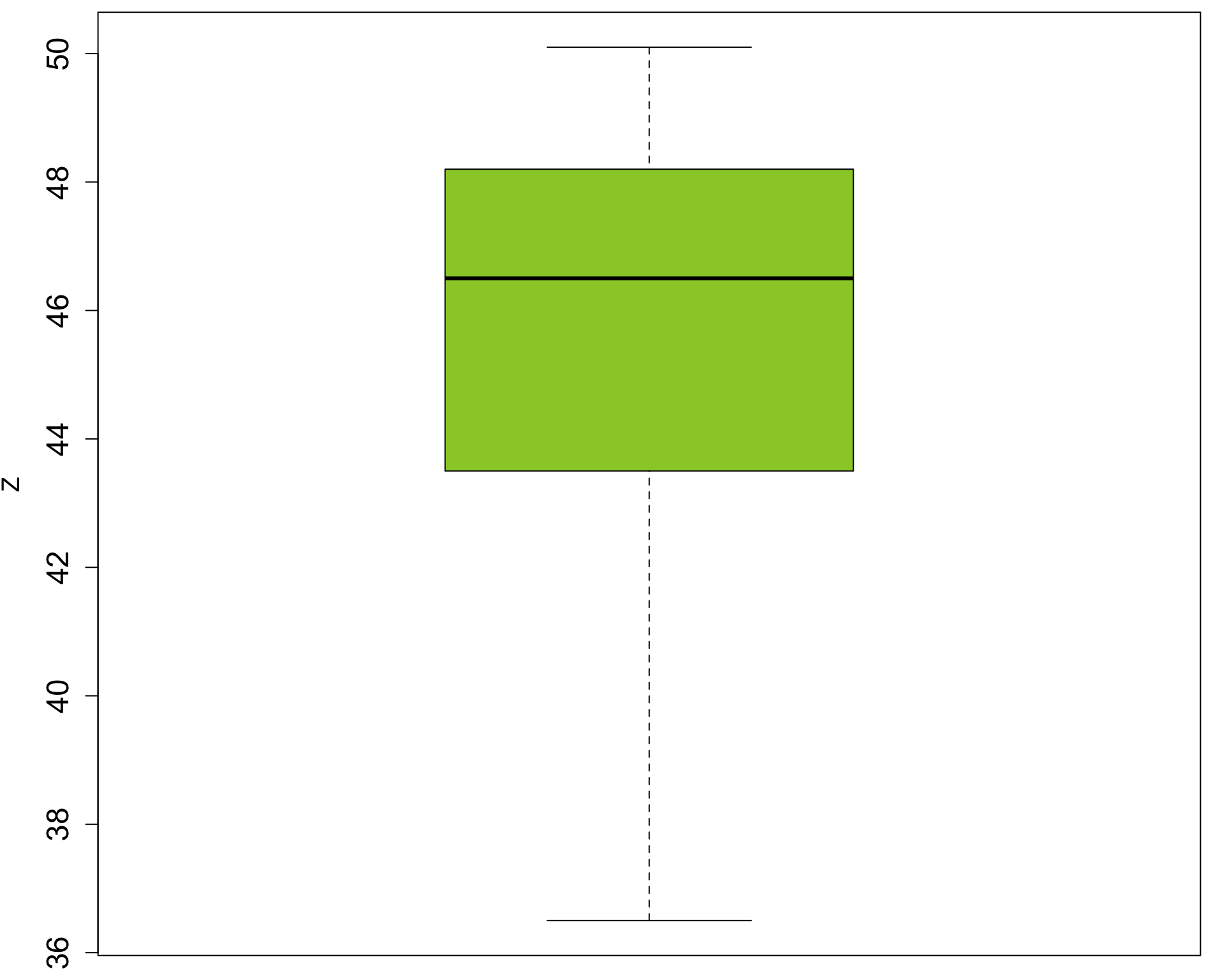
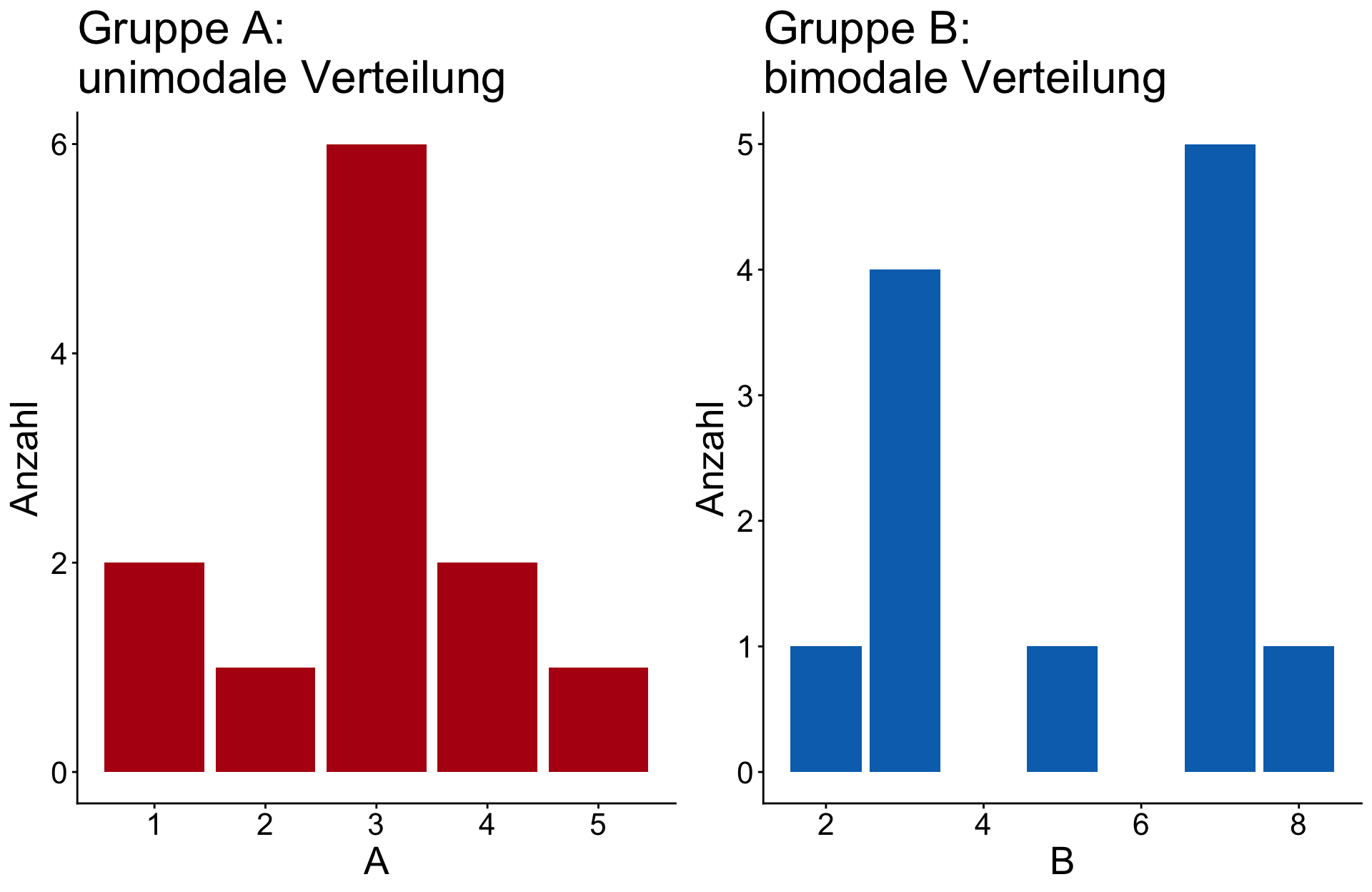
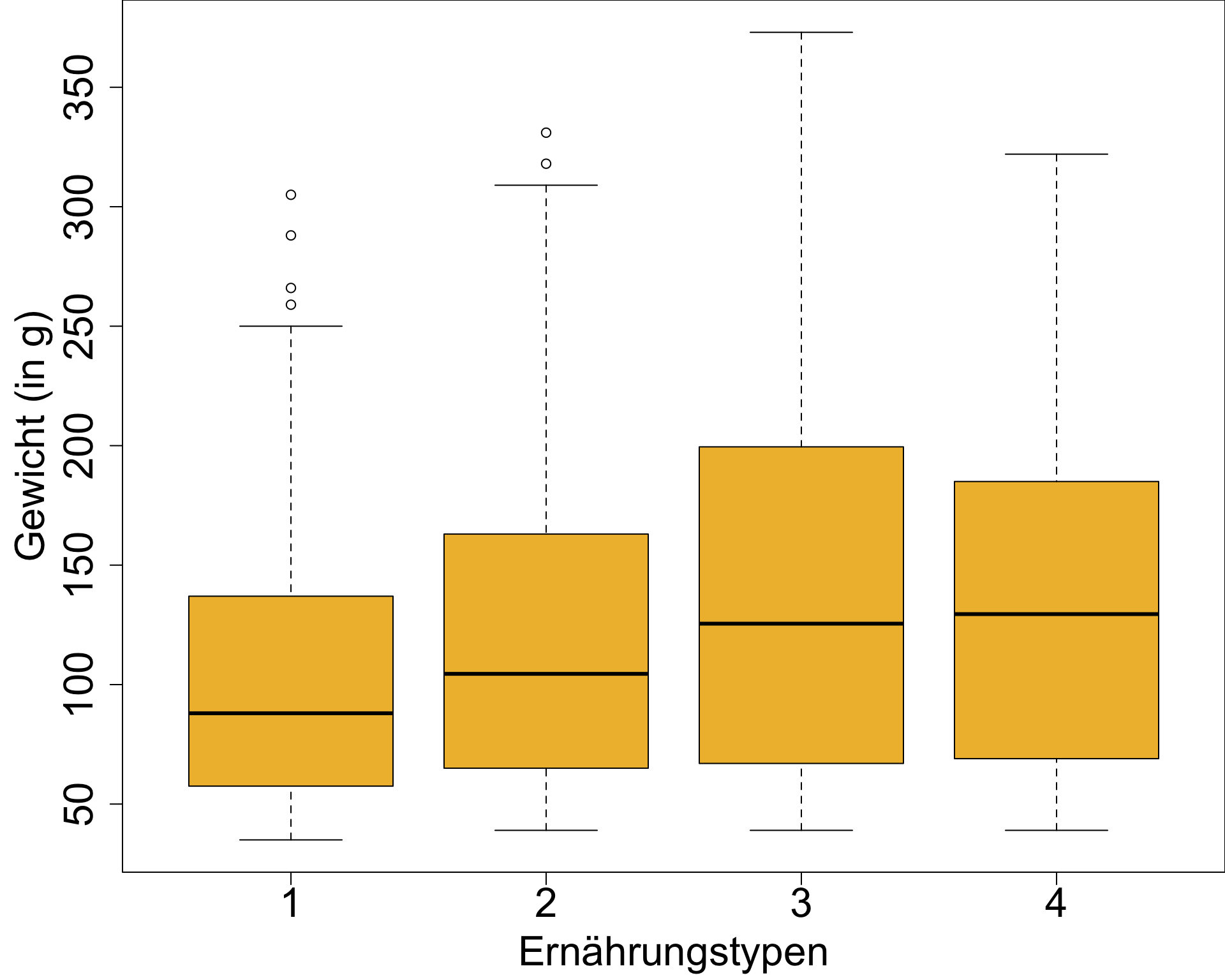
Quiz 8 | Vergleich von Verteilungen
![]()
Zurück zum Anfang ….
Wie würden Sie jetzt die Zusammenfassung interpretieren?

Automatische Zusammenfassung einer Statistik-Software
Übungsaufgabe
Übungsskript Woche 2

Wie fühlen Sie sich jetzt…?

Total konfus?

Dann schauen Sie doch mal in folgende Kurzvideos
- https://studyflix.de/statistik/deskriptive-statistik-1052
- Grafische Darstellungen: https://www.mathsisfun.com/data/index.html
Für Excel (Microsoft Office):
- Deskriptive Statistik
- https://www.youtube.com/watch?v=MTb-SVv5HuE (~12 min) oder
- https://www.youtube.com/watch?v=91YFVt9c95Q (~5 min)
- Histogramm
- Boxplot in Excel
Für Calc (LibreOffice):
Total gelangweilt?

Dann testen Sie doch Ihr Wissen in folgendem Abschlussquiz…
Abschlussquiz
![]()

Bei weiteren Fragen: saskia.otto(at)uni-hamburg.de

Diese Arbeit is lizenziert unter einer Creative Commons Attribution-ShareAlike 4.0 International License mit Ausnahme der entliehenen und mit Quellenangabe versehenen Abbildungen.
Kurswebseite: Data Science 1